Исследовательская работа "Математическое моделирование при решении задач на оптимизацию"

Министерство образования и науки РБ РФ

Научно-практическая конференция «Шаг в будущее»

МАОУ  СОШ  №37

Математическое моделирование

при решении задач на оптимизацию.

                                                                               Выполнил:

                                                                               Чой Влас,

                                                                               ученик 9 «а» класса

                                                                               Руководитель:

                                                                               Конева Галина Михайловна,

                                                                                  учитель математики, 

                                                                              «Отличник  просвещения РФ»,                      

Рецензия

на работу ученика 9 класса Чой Власа  по теме

«Математическое моделирование при решении задач на оптимизацию»

Большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Задачи подобного рода  носят общее название – экономические задачи на оптимизацию или экстремальные задачи. Экстремальные  задачи  с достаточной полнотой закладывают в сознание учащихся понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучшими. Решая задачи указанного типа, учащиеся видят, с одной стороны, абстрактный характер математических понятий, с другой – большую и эффективную их применимость к решению практических, жизненных задач. Такая постановка экстремальных задач способствует расширению сферы приложений учебного материала, повышает роль этих задач в осуществлении глубокой цели математического образования школьников – обучать приложению математики в различных областях человеческой деятельности. Экстремальные задачи помогают  школьнику ознакомиться с некоторыми идеями и прикладными методами школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности.  Решение экстремальных задач способствует углублению и обогащению математических знаний учащихся. Через задачи они знакомятся с экстремальными свойствами изучаемых функций. Неоценимую важность постановки экстремальных задач в школьном курсе математики я вижу также в воспитании исследовательской культуры учащихся. Ведь все решения таких задач предлагаются на уровне исследования математической модели и на уровне исследования реальной ситуации с использованием оптимизационных средств.

В данной работе ученик рассмотрел такие экстремальные задачи, которые решаются средствами элементарной математики: с помощью линейной и квадратичной функций, с помощью методов линейного программирования.

Учитель высшей категории: Конева Г.М.

                                                    План

1.           Введение

2.           Описание механизма решения задач на оптимизацию  через построение математических  моделей.

3.            Задачи, приводящие к исследованию линейной функции.

4.            Математическое программирование  как   область математики для решения  задач на экстремум функции многих переменных

5.            Задачи на оптимизацию, приводящие к исследованию  квадратичной функции.

6.           Заключение.

                                                                                                                  I.            Введение

  П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.  Итак, большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества.

  Задачи подобного рода  носят общее название – экономические задачи на оптимизацию. В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причем надо найти такое значение второй величины, при котором первая принимает своё наименьшее или наибольшее значение. Математикам удалось разработать методы решения задач на наибольшее и наименьшее значение, или, как их еще называют, задач на оптимизацию. Многие задачи  поиска оптимальных решений могут быть решены только с использованием методов дифференциального исчисления. Ряд задач такого типа решается с помощью специальных методов линейного программирования, но существуют и такие экстремальные задачи, которые решаются средствами элементарной математики.

  Следует различать также два вида задач на оптимизацию. В задачах первого вида улучшение достигается за счет коренных качественных изменений: выбор новых конструктивных решений, переход на новую технологию изготовления. В задачах второго рода качественная сторона дела остается неизменной, но меняются количественные показатели. В данной работе рассмотрены задачи только второго типа. В таких задачах ищутся наибольшее и наименьшее значения функций, зависящих от одной или нескольких переменных.

II. Математическое программирование как   область математики для решения задач на экстремум функции многих переменных

 Прежде чем решать какую – либо жизненную задачу, человек старается взвесить имеющуюся у него информацию, выбрать из нее существенную. И только потом, когда станет более или менее ясно, из чего исходить и на какой результат  рассчитывать, он приступает к решению задачи. Иногда описанный процесс называют “уяснением задачи”, фактически же это замена исходной жизненной задачи ее моделью. В осмыслении простейшей жизненной ситуации присутствует модельный подход, хотя человек обычно не замечает своей деятельности по созданию моделей – настолько она для него естественна. Иное дело, если возникающая задача затрагивает ключевые моменты жизни одного человека или какого – либо сообщества людей. Разнообразие информационных аспектов в каждой такой задаче настолько велико, что бывает сложно из всего многообразия информации об изучаемом явлении или объекте выбрать наиболее существенные. В таких случаях необходимо сделать упрощающее предположение, чтобы выделить исходные данные, определить, что будет служить результатом и какова связь между исходными данными и результатом. Все это – предположения, исходные данные, результаты, связи между ними – их называют моделью задачи.

  Если построенная модель дает удовлетворительные результаты при решении жизненных задач, то говорят, что модель адекватна рассматриваемому объекту (процессу или явлению). Нередко для решения модельной задачи требуется некоторый инструментарий. Этот инструментарий обычно организуется в виде единого объекта, называемого исполнителем. Чтобы исполнитель мог получить ответ, ему нужны указания, что и как делать. Такие указания часто представляются в виде алгоритма, в котором задаются математические соотношения, связывающие исходные данные и результат. В этом случае говорят о построении математической модели задачи.

  Обычно модель возникает как необходимый этап решения конкретной задачи. Однако в дальнейшем может происходить обособление модели от задачи, и модель начинает жить самостоятельно. Примером может служить сюжет движения с постоянной скоростью, который возникал в человеческой деятельности столь часто, что, в конце концов, обособился от задач и стал составляющей физического знания, называемого “равномерное прямолинейное движение”. Теперь при необходимости решить какую – либо задачу, связанную с равномерным движением пользуются этой готовой моделью процесса. В одних задачах результатом может оказаться время, в других – пройденный путь, в третьих скорость. Остальные параметры модели процесса станут исходными данными. Если же в задаче фигурирует не равномерное движение, а равноускоренное, то физика и здесь предложит готовую модель в виде формулы:

  Одним словом, все естественные науки, использующие математику, можно считать математическими моделями явлений. Например, гидродинамика является моделью движения жидкости, математическая экономика – моделью процессов экономики и т.д. До появления ЭВМ математическое моделирование сводилось к построению аналитической теории явления. Не всегда математическую теорию явления удавалось доводить до возможности вывода формул. Природа оказывалась сложнее возможностей аналитических методов математики. Приходилось вносить значительные упрощения в модель явления, а тем самым обеднять выводы. В этом веке математика пополнилась мощным математическим методом исследования: моделированием сложных систем на ЭВМ. Теперь исследователь ставит перед собой не ту цель, что раньше – вывод расчетной формулы. Теперь он стремится вычислять те или иные параметры, характеризующие явление. Таким путем были исследованы сложные вопросы, связанные с термоядерными реакциями, поведением самолетов в критических ситуациях, влиянием различных факторов на экологические системы, распространением эпидемий и пр.

  В настоящее время широко используется математическое моделирование и тогда, когда о физической структуре процесса известно крайне мало. В этом случае строится гипотетическая модель и на ее основе выводятся следствия уже доступные наблюдению. Если такие модели не оправдываются опытом, то они живут недолго и отмирают, уступив место другим моделям, позволяющим познать природу вещей точнее. История науки показывает, сколь большую роль сыграли научные гипотезы и построенные на их основе математические модели явлений. Математический аппарат, применяемый при построении моделей, весьма разнообразен. Кроме классических разделов математического анализа широко используются современные разделы математики, в которых изучаются методы, позволяющие находить оптимальные решения: линейное, нелинейное и динамическое программирование. Я изучил и исследовал такие экстремальные задачи, которые решаются с помощью исследования линейной и квадратичной функций, а также  с помощью методов линейного программирования.

III.      Экономические задачи на оптимизацию, приводящие к исследованию

линейной функции

Задача 1 . Расстояние между двумя фермами  А и В по шоссейной дороге 60 км. На ферме  А надаивают 200 т молока в сутки, на ферме В – 100 т в сутки. Где нужно построить завод по переработке молока, чтобы для его перевозки количество тонно-километров было наименьшим?

  Решение: Выясняем, что суммарное количество тонно-километров изменяется в зависимости от места нахождения завода, вычислив его, например, для случаев, когда завод находится от пункта А на расстоянии 30 км, 20 км, 10 км.

1)    Предположим, что завод построили на середине АВ, то есть завод будет находиться от пункта А на расстоянии  30 км. Найдем суммарное количество тонно-километров:

200т ∙30км + 100т ∙30 км= 9000т ∕ км

2)    Предположим, что завод построили  на  расстоянии 20 км от пункта  А.  Найдем суммарное количество тонно-километров:

200т ∙20км + 100т ∙40 км= 8000т ∕ км

3)    Предположим теперь, что завод построили  на  расстоянии 10 км от пункта  А.  Найдем суммарное количество тонно-километров:

200т ∙10км + 100т ∙50 км= 7000т ∕ км

Делаем предварительный вывод о том, что , чем ближе завод находиться к ферме А, тем меньше суммарное количество тонно-километров. 

Далее приступаем к решению задачи, обозначив расстояние от завода  С до фермы А через х: АС =х, ВС =60 – х. Количество тонно-километров, пройденных транспортом от А до С за каждый день, составляет 200 х т/км, а от В до С – 100 (60 – х) т/км. Суммарное количество тонно-километров выразится функцией

у = 200х + 100 (60 – х) = 100х + 6000,

 которая  определена на отрезке [0; 60].

  Ясно, что это уравнение может иметь бесконечно много решений. Естественно здесь поставить вопрос – найти дешевый вариант перевозок.  Исследуя функцию у = 100х + 6000 на отрезке [0; 60], получим:   = 6000.

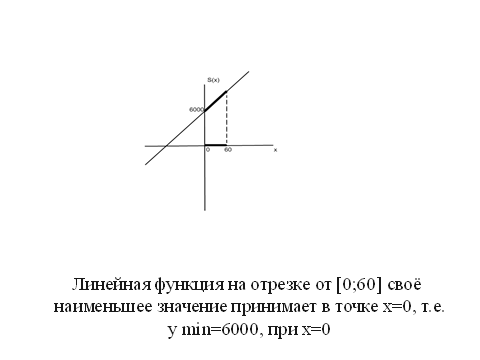
Эта линейная функция будет иметь минимальное значение при  х = 0,

  = 6000 т/км.

Вывод: Завод надо строить возле фермы А.

Для лучшего понимания этой задачи целесообразно дополнительно выяснить вопрос, где нужно бы построить завод по переработке молока , если бы:

а) на ферме  А надаивали  100 т, а на ферме  В – 200 т молока;

б) на ферме  А – 200 т, а на ферме  В – 190 т;

в) на ферме  А и на ферме  В – по 200 т молока;

Чтобы решить этот вопрос, нужно найти на отрезке [0; 60] минимум функции:

а) у = 100х + 200(60 – х) = - 100х + 12000;

б) у = 200х + 190(60 – х) = 10х + 11400;

в) у = 200х + 200(60 – х) = 12000.

Из всего этого можно сделать такой вывод: если на ферме   А добывается молока больше, чем на ферме  В, то завод надо строить возле фермы  А; если же количество молока на  этих фермах  одинаковое, то завод можно строить в любом месте вблизи шоссейной дороги между фермами  А и В.

Задача 2.

На дачном участке нужно провести водопровод длиной 167 м. Имеются трубы длиной 5 м и 7 м. Сколько нужно использовать тех и других труб, чтобы сделать наименьшее количество соединений (трубы не резать)?

Решение: Учитывая, что количество как одних, так и других труб может изменяться, количество 7 – метровых труб обозначим через х, а 5 – метровых – через у. Тогда 7х – длина 7-метровых труб, 5у – длина 5-метровых труб. Отсюда получаем неопределенное уравнение: 7х + 5у = 167, которое нужно решить в целых числах. Выразив, например, переменную у через переменную х, получим:

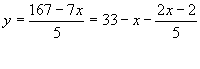 Так как х, у Є Z, то методом перебора легко найти соответствующие пары значений х и у, которые удовлетворяют уравнению  7х + 5у = 167.

Если 2х – 2 =0, то х = 1, у =32.

Если 2х – 2 =5, то х не является целым числом.

Если 2х – 2 =10, то х =6, у = 25.

Если 2х – 2 =15, то х не является целым числом.

Если 2х – 2 =20, то х = 11, у = 18.

Если 2х – 2 =25, то х не является целым числом.

Если 2х – 2 =30, то х = 16, у = 11.

Если 2х – 2 =35, то х не является целым числом.

Если 2х – 2 =40, то х = 21, у = 4.

Если 2х – 2 =45, то х = 23,5 , то есть не является целым числом.

Если 2х – 2 =50, то х = 26 и 7 ∙26 = 182 >167.

Итак, получили пары решений: (1; 32), (6; 25), (11; 18), (16; 11), (21; 4).Из этих решений наиболее выгодное последнее, т.е. х = 21, у = 4.

Вывод: Надо взять 21 трубу длиной по 7 метров и 4 трубы длиной по 5 метров.

Задача 3. Предположим , что населенный пункт С,  расположенный на отрезке АВ, снабжается некоторыми потребительскими  товарами  как из пункта А, так и из пункта В. Одна тонна этого товара из  А обходится в 5 тыс. руб., а из  В – в 7 тыс. руб. Транспортировка 1 т груза на расстояние 1 км стоит 200 руб. Расстояние между пунктами А и В равно 100км. Нужно составить такой план снабжения товарами пункта С,  при котором будет допускаться минимальный расход денег.

Решение: Попробуем представить эту жизненную ситуацию в математическом описании. Пусть расстояние АС = х, тогда ВС = 100 – х . Стоимость транспортировки 1т груза из пункта А в пункт С равна (5 + 0,2х)тыс. руб. Стоимость транспортировки 1 т груза из пункта В в пункт С равна: 7 + (100 – х) 0,2 тыс. руб, или (27 – 0,2х) тыс. руб. Узнаем, на каком расстоянии стоимость транспортировки груза от пункта А будет не больше, чем от пункта В, т. е.

5 + 0,2х ≤ 27 – 0,2х; 0,4х ≤ 22; х ≤ 55.

Вывод: Итак, из пункта А нужно транспортировать товар на расстояние не больше, чем на 55 км, а из В – не больше, чем на 45 км.  

IV. Математическое программирование  как   область математики для решения  задач на экстремум функции многих переменных

        Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества возможных вариантов в условиях рыночных отношений приходится отыскивать наилучшие при ограничениях, налагаемых на природные, экономические и технологические возможности. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем, математические методы и современную вычислительную технику. Такие методы объединяются под общим названием – математическое программирование.

         Математическое программирование – область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

          Функцию, экстремальное значение которой надо найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель. Математическая модель задачи – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д.

Модель задачи математического программирования включает:

1)совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют планом задачи.

2) целевую функцию. Целевая функция позволяет выбирать наилучший вариант из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Это может быть прибыль, объем выпуска или реализации, затраты производства. 

         Один из разделов математического программирования – линейное программирование, т.е.  направление, занимающееся методами решения задачи о минимуме линейных функций на выпуклых многогранниках (в многомерных пространствах). Линейным оно называется потому, что основывается на решении линейных уравнений. Неизвестные в них только первой степени; ни одно неизвестное не перемножается на другое неизвестное.

Такие уравнения отражают зависимости, которые могут быть изображены на графике прямыми линиями.  Также эти методы состоят в нахождении максимума и минимума линейной функции от нескольких переменных при заданных дополнительно ограничениях для этих переменных. Методы линейного программирования широко применятся во всех отраслях народного хозяйства. Особенно широкое применение они получили при решении задач экономии ресурсов.

Рассмотрим математическую суть этого метода на примере:

Задача 1

Для изготовления двух видов изделий Аи В завод расходует в качестве сырья сталь и цветные металлы, запас которых ограничен. На изготовление указанных изделий заняты токарные и фрезерные станки в количестве, указанном в таблице.

Необходимо определить план выпуска продукции, при котором будет достигнута максимальная прибыль, если время работы фрезерных станков используется полностью.

Решение: Посмотрим математическую модель задачи. Обозначим через  х- число изделий вида А, а через у – число изделий вида В. На изготовление всей продукции уйдет (10 х +70у)кг стали и (20 х +50у) кг цветных металлов. Так как запасы стали не превышают 320 кг, а цветных металлов – 420 кг, то

10х +70у  320
20х + 50у ≤ 420

(300х +400у) ч – время обработки всех изделий на токарных станках:

300х + 400у ≤ 6200

Учитывая, что фрезерные станки используются максимально, имеем:

200х +100у = 3400

Итак, система ограничений этой задачи имеет вид:

10х + 70у ≤ 320

20х +50у ≤ 420

300х + 400у≤6200       (1)

200х + 100у =3400

х≥ 0, у ≥ 0

Общая прибыль фабрики может быть выражена целевой функцией

F = 3х + 8у       (2)

Выразим у через x из уравнения 200х + 100у = 3400 и подставим полученное выражение вместо у в неравенства и целевую функцию:

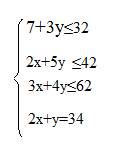
Преобразуем систему ограничений (3):

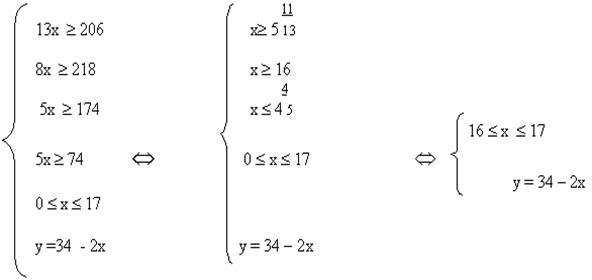
???Очевидно, что F =272 –3х принимает наибольшее значение, если х=16.

F_наиб = 272 – 13 ∙16 = 64 (тыс. руб.)

Вывод: х=16, y=2, прибыль – 64 тыс. руб.

Задача 2.

Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сети. Затраты на рекламу в бюджете фирмы ограничены величиной 1000$ в месяц. Каждая минута радиорекламы обходится в 5$, а каждая минута телерекламы - в 100$. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения, но при этом фирма решила, что время радиорекламы не должно превышать двух часов. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определите оптимальное распределение финансовых средств, ежемесячно отпускаемых на рекламу, между радио- и телерекламой. 
Решение: Обозначим за Хт - количество финансовых средств, отпускаемых на телерекламу, а за Хр - количество финансовых средств, отпускаемых на радиорекламу. Сразу же можем записать одно ограничение на общее количество средств, отпускаемых на рекламу: 
 
Количество минут, используемых для рекламы на радио, будет вычисляться следующим образом: , а количество минут, используемых для рекламы на телевидении:  
Для простоты будем считать, что время на рекламу можно покупать посекундно. Условие использования радиосети по крайней мере в два раза чаще, чем сеть телевидения, запишется следующим ограничением: 
 
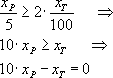
Решение о том, что время радиорекламы не должно превышать двух часов, запишется в виде: 
 
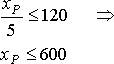
А теперь запишем целевую функцию. По условию задачи мы должны найти оптимальное значение распределения финансовых средств, чтобы эффективность от рекламы была максимальной. Если эффективность одной минуты радиорекламы обозначить за единицу, то эффективность одной минуты телерекламы будет равна двадцати пяти. Получим следующую функцию: 
 
Из условия задачи естественно вытекают ещё два ограничения: 
 
Сведем все ограничения и целевую функцию в одну систему: 
 

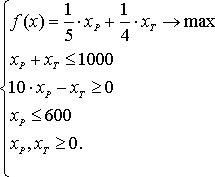
Решим систему графически:

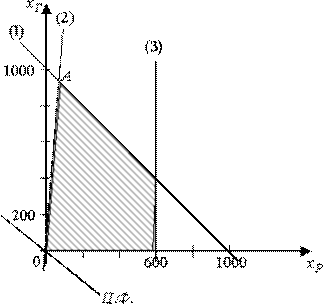
Точка А соответствует максимальному значению целевой функции.  
Таким образом, получили, что на радиорекламу надо тратить 90,90$, а на телерекламу - 909,09$, что в минутах составляет на радио - 18,18 минуты, а на телевидении - 9,9 минуты.

Задача 3

 Известно, что 1кг апельсинов содержит 150мг витамина С, а 1кг яблок  - 75 мг витамина С. сколько апельсинов и сколько яблок следует включить в дневной рацион, чтобы при минимальных затратах в нем оказалось 75 мг витамина С, не менее 0,25кг апельсинов и не менее 0,25кг яблок, если 1кг апельсинов стоит 30р., а 1кг яблок – 20р.?

Занесем данные в таблицу:

Ограничения имеют вид:

х ≥ 0,25                     х ≥ 0,25          х ≥ 0,25   

у ≥ 0,25                     у ≥ 0,25          у ≥ 0,25

150х + 75у = 75        2х + у = 1      у = -2х +1

Целевая функция: F (х, у) = 60х + 40у

Необходимо найти такие х и у, при которых целевая функция принимает минимальное значение. Построим область допустимых решений задачи:

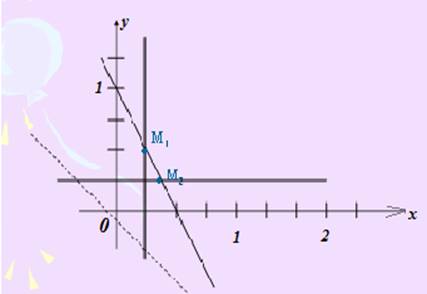
Пусть 60х + 40у = 0; отсюда у = -6/4х

Построим график функции у = -6/4х и будем осуществлять параллельный перенос его вдоль оси ОУ вверх, т.е. это равносильно увеличению значений выражения 60х + 40у.

Чтобы целевая функция принимала минимальное значение, ее график должен пересечь отрезок М₁М₂  в точке М₂. Она является точкой пересечения прямых

у = 0,25 и у = -2х +1.

Решение системы уравнений:

у = 0,25           у = 0,25                  у = 0,25                 

у = -2х +1        -2х +1 = 0,25         х = 0,375

Далее находим: F (х, у) = 60∙0,375 + 40∙0,25 = 16,25р.

Итак, чтобы дневной рацион содержал 75мг витамина С и чтобы затраты при этом были минимальные, человеку необходимо ежедневно съедать 0,375кг апельсинов и 0,25кг яблок.

IV.       Использование  свойств  квадратичной  функции при решении экстремальных задач

Задача 1.

Окно имеет форму прямоугольника ,завершенного полукругом. Периметр фигуры равен 6м. Каковы должны быть размеры окна, чтобы окно пропускало наибольшее количество света?

Решение: Окно будет обладать наибольшей пропускной способностью, если при заданном периметре будет иметь максимальную площадь.

Пусть AB = x, AD = y, тогда

P=AB+BC+AD+ DMC

P=x+2y+0,5 π x (1)

S=AB∙BC+π x /8

S=xy+ x π /8 (2)

Из (1),(2) следует, что

S(x)=-(π /8 +1/2)x² +3x

Известно, что квадратный трехчлен принимает наибольшее значение при

x =-b/2a,т.е. x =12/(π +4), y= 6/ (π +4).

Ответ: Размеры окна 6/(π +4), 12/(π +4).

Задача 2. Для строительства склада заготовлен материал на наружные стены длиной 32 м и высотой 4 м. Какими должны быть размеры  склада (в виде прямоугольного параллелепипеда), чтобы  он имел наибольший объём?

Решение задачи сводится к исследованию функции:  

V = х (16 – х)4 = - (2х – 16)² + 256 ≤ 256, где х – длина. Значит, 2х -16=0,  х = 8.

 Вывод. Итак, чтобы объем склада был наибольшим, его размеры должны быть 8× 8 ×4.

V.          Заключение.

  В настоящее время получило всеобщее признание то, что успех развития многих областей науки и техники существенно зависит от развития многих направлений математики. Математика становится средством решения проблем организации производства, поисков оптимальных решений и, в конечном счете, содействует повышению производительности труда и устойчивому поступательному развитию народного хозяйства.

  Использование экстремальных задач при изучении математики оправдано тем, что они с достаточной полнотой закладывают понимание того, как человек ищет, постоянно добивается решения жизненных задач, чтобы получающиеся результаты его деятельности были как можно лучше. Решая задачи указанного типа, наблюдаем, с одной стороны, абстрактный характер математических понятий, а с другой – большую эффективную их применимость к решению жизненных практических задач.

  Экстремальные задачи помогают ознакомиться с некоторыми идеями и прикладными методами школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности.

  Решение экстремальных задач способствует углублению и обогащению наших математических знаний. Через задачи мы знакомимся с экстремальными свойствами изучаемых функций, с некоторыми свойствами неравенств. Эти задачи могут серьезно повлиять на содержание учебного материала, на аспекты применения положений изучаемой теории на практике.

VI. Список литературы

1.            Беляева Э. С., Монахов В.М. Экстремальные задачи. М.: Просвещение, 1997.

2.            Виленкин Н. Л. Функции в природе и технике. – М.: Просвещение, 1978

3.            Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.: Просвещение, 1985.

4.            Гейн А. Г. Земля Информатика. – Екатеринбург: Издательство Уральского университета, 1997

5.            Гнеденко Б. В. Введение в специальность математика. – М: Наука, 1991

6.            Гнеденко Б. В. Математика в современном мире. М: Просвещение, 1980.

7.            Перельман Я. И. Занимательная алгебра. М: АО “Столетие”, 1994

8.            Хургин Я. И. Ну и что? (Разговоры математика с биологами и радистами, врачами и технологами… о математике и ее связях с другими науками). М.: Молодая гвардия, 1987.