Исследовательская работа "Теория чисел"

Содержание

Введение …………………………………………………………………………3

1. Теория чисел на уроках математики в средней школе…………………….5

2. Задачи теории чисел………………………………………………………….6

2.1. Теория чисел на уроках математики……………………………………….6

2.2.Олимпиадные и марафонные задачи по теории чисел……………………7

2.3. Задания типа 19 из КИМов ЕГЭ базовой математики……………............8

Заключение……………………………………………………………………….11

Список литературы………………………………………………………………12

Приложение 1 ……………………………………………………………………13

Приложение 2 ……………………………………………………………………14

Приложение 3 ……………………………………………………………………15

Введение

    Теория чисел или высшая арифметика – раздел математики, изучающий целые числа.   В теории чисел в широком смысле рассматриваются  алгебраические числа, которые связаны с арифметикой целых чисел, и их обобщения.

   В  элементарной теории чисел  целые числа  изучаются без использования  методов  других разделов  математики. Изучаются такие вопросы,  как делимость чисел,  разложение числа на простые множители, составление чисел, удовлетворяющих заданным условиям.

Актуальность.  Математики не любят много писать. Длинные предложения и повторы одних и тех же слов хороши при объяснении решения, но при его записи желательно пользоваться условными обозначениями, которые упрощают запись решения, что я и хочу показать в свой работе, как, не теряя много времени, решать задачи по теории чисел.

Объект исследования: натуральные числа.

Предмет исследования: задачи по теории чисел, решаемые  с помощью признаков делимости, задачи ЕГЭ типа 19.

Цель: описание методов и способов решения задач по теории чисел, научиться составлять числа из цифр  удовлетворяющих заданным условиям.

В соответствии с целью исследования необходимо решить следующие задачи:

- повторить признаки делимости;

- изучить признаки делимости составных чисел, рассмотреть методы и  способы решения задач по теории чисел;

- описать методы и способы решения логических задач  в 5 - 6 классах, - научиться решать 19 задачи ЕГЭ.

Методы исследования: сбор информации, обработка данных, сравнение, анализ.

Гипотеза: Если знаешь признаки делимости и свойства чисел, можно научиться решать задачи по теории чисел.

1.                 Теория чисел на уроках математики в средней школе.

Основной объект теории чисел - натуральные числа. Главное их свойство, которое рассматривает теория чисел - это делимость. Первый круг задач теории чисел - разложение чисел на множители. Основными «кирпичиками» в таком разложении являются простые числа. Замечательная теорема, называемая основной теоремой арифметики, гласит: всякое натуральное число раскладывается на простые множители, причем единственным способом (с точностью до порядка их расположения). Разложив два числа на простые множители, несложно определить, делится одно из них на другое или нет.

Теория чисел привлекательна тем, что в ней много простых по формулировкам, но трудных и интересных задач. Этих задач - решенных и нерешенных - накопилось очень много, и часто теория чисел представляется собранием разрозненных изящных головоломок. Однако это не так. Теория чисел - создала свои замечательные методы, причем многие из них активно развиваются в последние время, что влило новую живую струю в эту самую древнюю часть математики.

Чем особенно ценна теория чисел? Ведь найти непосредственное применение ее результатам трудно. Тем не менее, задачи теории чисел привлекают как молодых людей, так и ученых в течение многих столетий. В чем же здесь дело? Прежде всего, эти задачи очень интересны и красивы. Во все времена человека поражало, что на простые вопросы о числах так трудно найти ответ. Поиски этих ответов часто приводили к открытиям, значение которых далеко превосходит рамки теории чисел.

Меня тоже заинтересовала эта тема,  и  я попытался рассмотреть в своей работе некоторые задачи.

2.Задачи теории чисел.

2.1. Теория чисел на уроках математики в средней школе.

   Для начала рассмотрим несколько задач из нашего учебника математики Н.Я.Виленкина.

       При изучении признаков делимости на уроках математики мы столкнулись с задачами по теории чисел: поставить вместо * цифры , чтобы получившееся число делилось на заданное, сколько можно составить чисел – трехзначных, четырехзначных из заданных цифр и т.д.

Например:

1.                 В записи числа  *723,  5*36, 111* вместо звездочки поставьте такие цифры, чтобы полученное число делилось на 9.

Решение: по признаку делимости на 9 нужно  подставить

*723  - 6

5*36 - 4

111* - 6

2.                 Сколько трехзначных чисел можно составить из нечетных чисел?

Решение:

Выпишем все нечетные цифры 1,3,5,7,9

*** - число трехзначное, значит, на первое место можно подставить все 5 цифр, на второе тоже - все5 и на третье тоже 5.

Находим произведение 5 × 5 × 5= 125

Ответ:125 чисел

3.                 Решим вторую задачу при условии, что цифры не повторяются.

*** - число трехзначное, т.к. цифры не повторяются,

на последнее место можно подставить все пять цифр;

на второе только 4, т.к. одну цифру мы поставили уже на последнее место;

на первое место только 3, т.к. две цифры уже на втором и третьем местах;

значит, 3×4×5=60    Ответ: 60 чисел

 2.2.  Олимпиадные и марафонные задачи.

Задача 1.На районном марафоне нам была предложена задача: Сколько четырехзначных нечетных чисел можно составить из цифр  0,1,2,3,4?

Решение: * * * * - число четырехзначное

На последнее место мы можем подставить только 1 или 3, т.к. в остальных случаях получается четное число, значит, 2 цифры;

 на первое место все цифры кроме нуля, значит 4 цифры;

на второе и третье место можно подставить все 5 цифр.

Итак, 4×5×5×2=200   Ответ: 200 чисел

Задача 2.Олимпиадная задача. Докажите, что число 13026970 делится на 55.

Решение: Для решения этой задачи нет необходимости выполнять деление столбиком, достаточно разложить 55 на простые множители 55=5×11 и проверить делимость на 11 и 5.  Число делится на 5, т.к. последняя цифра 0, число делится на 11, т.к. 1+0+6+7=14

                                             3+2+9+0=14

Значит, и число делится на их произведение.

Для решения олимпиадных задач еще нужно знать теорему о делимости произведения натуральных чисел.

Теорема: Если в произведении хотя бы один из сомножителей делится на некоторое число, то и произведение делится на это число.

Задача 3. Докажите, что произведение  475×1230×800 делится на 6.

Решение: 

- Чтобы произведение делилось на 6, оно должно делиться и на 2 и на 3,

- среди чисел есть четное число, значит, произведение делится на 2,

- сумма цифр числа 1230 есть 1+2+3+0=6, 6:3, значит, число делится на 3,

- условия делимости на 2 и на 3 выполняются, значит, число делиться на 6.

Задача 4. Докажите, что число 4356 можно представить в виде квадрата трех множителей.

Решение: Разложим число на простые множители.

Получаем   4356=2×2×3×3×11×11 ,  а это значит, что

4356= 2²×3²×11²=(2×3×11)²    ч.т.д.

2.3. Задания типа 19 из КИМов ЕГЭ базовой математики.

Для решения заданий типа 19 достаточно знать признаки делимости и разложение числа на простые множители.  А простыми называются числа, которые делятся на себя и на 1.

Например: 3 простое число, 3:3 и 3:1

А раскладывать лучше постепенно. Например: 60=2×2×3×5

Начнем с самых простых задач ЕГЭ.

Задача 1.19. Вычеркните в числе 181615121 три цифры так, чтобы полученное число делилось на 12. В ответе укажите какое-нибудь такое число.

Решение: Раскладываем делитель числа 12 на простые множители 12=4×3=2×2×3.  Следовательно, число после вычеркивания должно делиться на 4 и на 3  или на 3, на 2 и еще раз на 2.

На 2 делятся четные числа, поэтому 1 в конце вычеркиваем сразу.

Нам нужно, чтобы оно делилось на 4. По признаку делимости на 4 последними могут быть цифры 1 и 2, т.е. 12:4=3

По признаку делимости на 3

1+8+1+6+5+1+2=25. Т.к.  последние две цифры трогать нельзя  25=3×6+7  вычеркиваем две цифры, сумма которых равна 7, т.е. 6 и любую из единиц, кроме последней.

   Итак, возможные ответы:  811512  или 181512. В ответ выбираем один из них.

Задача 2.19. Найдите шестизначное натуральное число, кратное 12, произведение цифр которого равно 40.  В ответе укажите какое-нибудь одно такое число.

Решение: 40=2×2×2×5, т.к. множителей недостаточно для пятизначного числа, то в произведение можно всегда добавить единицу.

Чтобы число делилось на 12, он должно делиться на 3 и на 4.

Проверяем делимость на 3:  1+2+2+2+5=12, значит, число может состоять из этих цифр.

А для выполнения признака делимости число должно оканчиваться  на 12 или на 52, а в начале любые перестановки из остальных цифр.

52212                   12252

25212                    21252

22512                   22152

В ответ можно записать один из них.

Задача 3.19.   Приведите пример трехзначного натурального числа,  которое при делении на 4 и на 15 дает равные ненулевые остатки,  и первая справа, цифра которого является средним арифметическим двух других цифр.

Решение: по условию число должно делиться на 4, на 5, на 3. Т.к. 15=3×5.

И еще число делится на 4 и на 15, если делится на их произведение     4×15=60. Возьмем трехзначные числа 120 и 180, делящиеся на 60. Эти числа не удовлетворяют условие, т.к. среднее арифметическое первых двух чисел не натуральное число, а десятичная дробь. Берем 240, оно делится и на 4, и на 5, и на 3.

А всем данным условиям  отвечает число 243.
Крайняя справа цифра - 3 - равна среднему арифметическому чисел 2 и 4, и 243 = 4*60 + 3 = 15*16 + 3 - остатки от деления этого числа на 4 и 15 равны.

Еще удовлетворяют числа 423 или 603.

В ответ можно записать один из них.

Задача 4.19.  Найдите четырехзначное число, кратное 4, сумма цифр которого равна их произведению. В ответе укажите какое-нибудь одно такое число.

Решение:  т.к. сумма цифр равна произведению, большие цифры мы не можем взять.  По признаку делимости на 4 возьмем двузначное число кратное 4 и состоящее из маленьких цифр -  это 12 и  24. Поставим одно их них на последнее место.  Остальные две цифры находим способом подбора:

4112 или 1412 или 1124. Во всех случаях сумма цифр  равна произведению цифр.

В ответ можно записать один из них.

ЗАКЛЮЧЕНИЕ

 Зная методы исследований признаков делимости натуральных чисел, можно научиться решать задачи по теории чисел, олимпиадные задачи по теме, задания ЕГЭ типа 19.  Я  попробовал решить такие  задачи вместе с учащимися старших классов (Приложение 1).

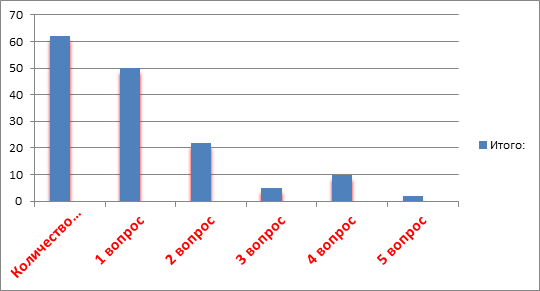
Изучив тему,  мы провели опрос учащихся 6-11 классов нашей школы  в виде небольшой анкеты (Приложение 2).

Результаты опроса показали, что учащиеся знают разложение числа на простые множители, знают признаки делимости,  а как использовать их при решении задач, знают лишь учащиеся 10-11классов.

К работе я еще приложил Приложение 3: брошюру «Признаки делимости» которую  я вместе с моим учителем подготовил в прошлом году, буклет «В помощь учителю».  

Надеюсь, что моя работа найдет практическое применение на уроках математики и при подготовке  к экзаменам.

Считаю, что цели и задачи исследовательской работы полностью реализованы.

СПИСОК ЛИТЕРАТУРЫ

1. Савин А.П. «Энциклопедический словарь юного математика», - Изд.: Москва «Педагогика», 1999год.

2. Виленкин Н.Я. « За страницами учебника математики», - Изд.: Москва «Просвещение», 1996 год.

3. Математическая шкатулка: Пособие для учащихся 4-8 кл. сред. шк. 5-е изд. - М.: Просвещение, 1988.

4. Виленкин Н.Я., Жохов В.И., Чесноков А.С., С.И. Шварцбурд «Математика,6», -  Изд. Мнемозина, Москва, 2015

5.И.В.Ященко, Типовые экзаменационные варианты по математике, ЕГЭ 2017 базовый уровень, изд. «Национальное образование», Москва, 2017

                                                                                     Приложение 1

Рис.1  На дополнительных занятиях с учащимися старших классов

Рис.2   На занятиях по внеурочной деятельности «Занимательная математика»

                                                                    Приложение 2

Анкета

Вопросы:

1.Знаете ли вы признаки делимости?                                                     Да Нет

2. Знаете ли вы как разложить число на простые множители?        Да Нет

3. Умеете ли вы решать задачи по теории  чисел?                              Да Нет

4.Умеетели вы решать задачи ЕГЭ типа 19?                                        Да Нет

5.Легко ли вам решать задачи типа 19?                                                Да Нет

Результаты опроса:

                                                                            Приложение 3

Буклет «В помощь учителю»

Брошюра «Признаки делимости»

Скачано с www.znanio.ru