Исследовательский проект по математикена тему: «Комбинаторика вокруг нас»

Содержание

Введение

Тема данного исследовательского проекта: «Комбинаторика вокруг нас».

Целью работы является освоение теоретических аспектов комбинаторики, изучение применения комбинаторики в различных областях жизнедеятельности человека и подготовка к проведению просветительского мероприятия на тему «Комбинаторика вокруг нас».

Для достижения цели были поставлены и решены следующие задачи:

- рассмотрены основные понятия комбинаторики;

- изучены правила сложения и умножения в комбинаторике;

- освоено сочетания и размещения с повторениями и без повторений;

- проанализировано применение комбинаторики на шахматной доске;

- рассмотрены пароли и коды в нашей жизни и их связь с комбинаторикой;

- проведен анализ общих знаний комбинаторики у студентов группы П-111 Белгородского правоохранительного колледжа имени Героя России В.В. Бурцева.

Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации. И целый раздел математики, называемый комбинаторикой, занят поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае.

В жизни общества большое место занимают азартные игры. Проблемы азартных игр и явились движущей силой развития комбинаторики.

Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицу, показывающую, сколькими способами могут выпасть р костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами.

Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв с использованием ключевых слов и т. д.

Стали выходить журналы по комбинаторике, печататься книги, посвященные этой науке. Элементы комбинаторики находили отражение и в школьном курсе математики.

При выполнении исследовательского проекта была использована учебная литература и ресурсы Интернет.

Работа выполнена на 28 страницах машинописного печатного текста, содержит 3 таблицы и 7 рисунков.

1. Теоретическая часть

1.1 Что такое комбинаторика в математике

Комбинаторика (комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана с другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Разделы комбинаторики представлены на рисунке 1.

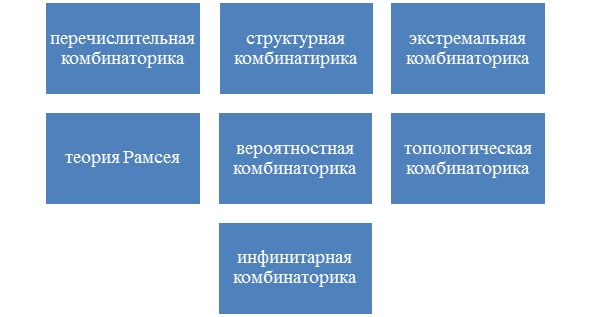
Рисунок 1 - Разделы комбинаторики

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчете количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определенные ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т.п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчет количества перестановок.

Структурная комбинаторика – это раздел комбинаторики к которому относятся некоторые вопросы теории графов. Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединенных ребрами. В строгом определении графом называется такая пара  множеств , где V есть подмножество любого счетного множества, а E - подмножество V×V.

Теория графов находит применение в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи — как ребра. Применение различных вычислений, производимых на таком графе, позволяет найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Примером раздела экстремальной комбинаторики может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определенным свойствам.

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

- в группе из 6 человек всегда можно найти трех человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

- в любом графе с 6 вершинами найдется либо клика, либо независимое множество размера 3 (рис. 2).

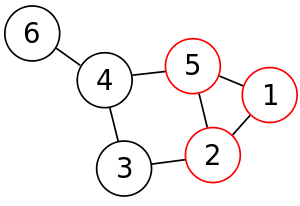
Рисунок 2 – Граф с кликой размера 3.

Кликой в неориентированном графе называется подмножество вершин, каждые две из которых соединены ребром графа.

Вероятностная комбинаторика отвечает на вопросы вида: какова вероятность присутствия определенного свойства у заданного множества.

Топологическая комбинаторика применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчетным) множествам.

Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов, – возникла в XVI в., но как наука стала развиваться в XVIII в. параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов.

 В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока Шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля» (рис. 3).

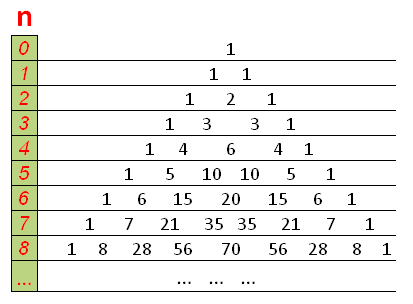
Рисунок 3 - Треугольник Паскаля

Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

- задача о ходе коня;

- задача о семи мостах, с которой началась теория графов;

- построение греко-латинских квадратов;

- обобщенные перестановки.

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Задача, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называются комбинаторикой. Комбинаторику можно рассматривать как часть теории множеств – любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях.

1.2 Основные понятия

n– факториал ‒ произведение первых n ‒ натуральных чисел (обозначается n!)

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

- размещение;

- перестановка;

- сочетание;

- композиция чисел;

- разбиение числа.

Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.    

Перестановкой из n элементов называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n и вычисляется по формуле 

Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов, считаются одинаковыми, этим сочетания отличаются от размещений.

Свойства сочетаний:

.

На рисунке 4 представлен алгоритм выбора формулы для вычисления количества комбинаций.

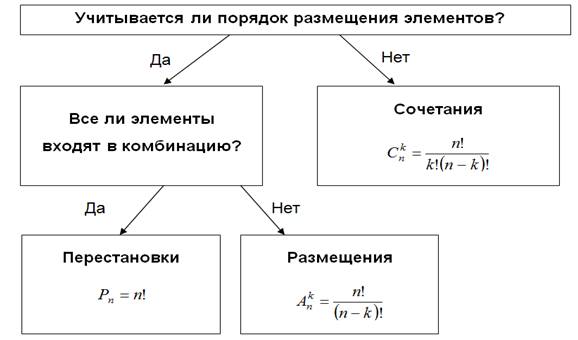
Рисунок 4 – Алгоритм выбора формулы при решении комбинаторных задач

Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.

Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

1.3 Правила сложения и умножения в комбинаторике

Правило суммы гласит, что если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m  способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:  способами.

1.4 Сочетания и размещения с повторениями и без повторений

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать k из n различных предметов?

Пусть имеется множество N из n элементов. Всевозможные неупорядоченные подмножества из k элементов, составленные так, что любой элемент множества N может входить в эти подмножества от 1 до k раз, либо вообще отсутствовать, называются сочетаниями с повторением. Их число подсчитывают по формуле:

.

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить  по k различным местам k из n различных предметов?

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по k различным местам k из n предметов, среди которых есть одинаковые?

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

В комбинаторных задачах удобно пользоваться таблицей 1.

Таблица 1 – Основные формулы при решении комбинаторных задач

2 Комбинаторика в различных областях жизнедеятельности человека

2.1 Комбинаторика на шахматной доске

К шахматам можно относиться как к науке со своими законами и принципами. Шахматы содержат в себе элементы научного исследования – именно такой подход свойственен многим выдающимся шахматистам. Задачи, связанные с шахматной теорией, а именно с комбинаторикой, широко применяются в математике.

Шахматы появились в Индии в VI веке нашей эры. Точная Дата возникновения шахмат и имя изобретателя неизвестны. Свое название игра берет из персидского языка. «Шах» означает король, а «мат» - умер. И по сей день изобретаются все новые и новые виды шахмат. Почти во всех видах шахмат, правила не меняются, меняется только способ расстановки фигур или добавляются новые фигуры.

Согласно одной гипотезе шахматная доска произошли из так называемых магических квадратов. Магический квадрат обладает следующим свойством: сумма чисел каждой строки, каждого столбца, а также двух главных диагоналей одна и та же. Для магических квадратов порядка 8 она равна 260.

Исследование геометрии шахматной доски приводит к разработке алгоритмов для известных и широко применяемых на практике интуитивных правил «квадрата», «треугольника» или «линии Троицкого», позволяющих оценить качество позиции не только на много ходов вперед, но и окончательно, как в приведенных случаях. Более того, при геометрическом анализе позиции в шахматной партии могут возникать и так называемые экстремальные задачи. Их решение помогает отыскивать мат за наименьшее количество ходов.

Основной способ поиска наилучшего хода заключается в переборе возможных ходов, рассмотрении движения по дереву последовательных позиций и оценке возникающих в результате них состояний игры. Играющему для подсчетов вариантов приходится тратить много времени даже в случае использования компьютера. Поэтому при поиске наиболее эффективных алгоритмов в компьютерных шахматах принято учитывать как можно больше ограничений (условий), упорядочивающих перебор, позволяющих отбрасывать те позиции, которые при выборе хода рассматривать не нужно. Эти задачи представляют из-за чего получили распространение эвристические методы их решения (метод перебора).

1 июня 1850 года в «Иллюстрированной газете» под рубрикой «Шахматы» была напечатана следующая задача: расставить 8 ферзей (королев) на шашечнице так, чтобы ни один ферзь не угрожал другому.

В общем виде задача о 8-ми ферзях формулируется следующим образом: на квадратной шашечнице из n²  клеток расставить n ферзей так, чтобы ни один не угрожал другому. Определить число всех решений.

В более «математическом» виде задача может быть сформулирована несколькими способами, например, так: «Заполнить матрицу размером 8×8 нулями и единицами таким образом, чтобы сумма всех элементов матрицы была равна 8, при этом сумма элементов ни в одном столбце, строке или диагональном ряде матрицы не превышала единицы».

Общее число возможных расположений 8 ферзей на 64-клеточной доске равно . Современные компьютеры позволяют произвести решение задачи (нахождение любого или всех решений) путем прямого перебора всех возможных вариантов расстановки. Общее число возможных расположений, удовлетворяющих условию задачи, равно 92.

Задача этого типа сформулирована и для других фигур, а именно для ладей и слонов, но в этих случаях решение может быть получено несравненно легче.

Клод Шеннон и Михаил Ботвинник внесли огромный вклад в создание математической модели шахматной игры и способствовали прогрессу в интеллектуализации программ для нее.

Впервые компьютерная шахматная программа  Deep Blue фирмы IBM обыграла чемпиона мира Каспарова при стандартном часовом контроле в 1996 году. Однако Каспаров изменил свой стиль игры, выиграв три и сведя вничью две из оставшихся пяти партий. Правила позволяли разработчикам изменять программу между играми. Deep Blue был изменен между партиями для лучшего понимания машиной стиля игры Каспарова, помогая избежать ловушки в эндшпиле, в которую дважды попадал искусственный интеллект. В мае 1997 года усовершенствованная версия Deep Blue нанесла поражение Каспарову со счетом 3,5-2,5.

По существу компьютерные шахматы — едва ли не самый убедительный пример за полвека развития информационных технологий, когда именно в интеллектуальной деятельности автомат успешно соперничает с человеком.

2.2 Пароли и коды в нашей жизни

В современном мире высоких технологий нас окружают всевозможные коды, которые управляют работой любого гаджета. Все компьютерные программы написаны с использованием двоичного кода. От расстановки единиц и нулей в коде зависит работа и назначение той или иной программы.

Даже если не рассматривать самый очевидный пример использования паролей и кодов, в нашей жизни коды встречаются повсеместно, начиная с даты нашего рождения.

Астрологи и нумерологи утверждают, что дата нашего рождения, это некий код, который откладывает отпечаток на наш характер и судьбу в целом.

Слова которыми мы пользуемся в обычной жизни можно тоже представить как коды, значение которых понятно всем. Но во время войны появилась необходимость шифровать послания так чтобы истинный смысл не был понятен врагу в случае перехвата послания. Для этого были придуманы всевозможные шифры, которые невозможно было взломать не разгадав код.

Методом шифрования (шифром) называется совокупность обратимых преобразований открытой информации в закрытую информацию в соответствии с алгоритмом шифрования. Большинство методов шифрования не выдержали проверку временем, а некоторые используются и до сих пор.

Шифр Цезаря – на основе его разработаны все шпионские шифры, начиная с 10 века до нашей эры. Основой служит сдвиг, одной буквы вправо на один символ.

Шифр Вижнера, состоит из (квадрата) матрицы букв русского алфавита. Шифрование символа происходит путем сдвига буквы в каждой строке алфавита на одну позицию вправо.

Ручные методы шифрования  занимали огромное количество времени и были недостаточно эффективны. Шифрование небольшого приказа занимало до 6 часов работы, примерно столько же требовалось на то, чтобы расшифровать полученное сообщение.

В 1937 году в Ленинграде на заводе «209», был образован комбинат создававший шифровальную технику для скрытого управления войсками: в 1939 году была создана шифровальная машина, которая получила название М-100. Основным недостатком этой машины был их огромный вес. Устройство весило 141 килограмм.

В 1939 году была запущенна в серийное производство шифровальная машина К-37 «Кристалл», и к началу войны на вооружение шифр органов СССР было принято свыше 150 комплектов шифровальных устройств К-37.

В годы войны на машинную шифросвязь легли огромные нагрузки. Только шифровальной службой РККА (8-й отдел) было принято 1,5 миллиона шифротелеграмм и кодограмм, а разослано почти 3,3 миллиона комплектов шифров.

В годы войны была изобретена шифровальная машина под названием «Энигма». Первая — модель А — была большой, тяжелой (65x45x35 см, 50 кг), похожей на кассовый аппарат. В 1928 году появилась Enigma G, она же Enigma I, она же «Энигма вермахта»; имея коммутационную панель, отличалась портативностью и усиленной криптостойкостью и работала в сухопутных войсках и ВВС. Устройство этой шифровальной машины довольно простое. В один из ее отделов вводят незашифрованное сообщение. Пройдя через машину, под воздействием различных электрических импульсов оно превращается в зашифрованный текст и выводится из другого отдела машины. Ключом, который постоянно меняется, обладает другая «Энигма», принимающая сообщение. Через нее оно проходит в обратном направлении, и текст из зашифрованного превращается в обычный. Даже заполучив машину, противник не сможет ею воспользоваться: она надежно хранит свои тайны, а регулярно меняющийся ключ очень скоро, максимум через месяц, сделает ее трофейным музейным экспонатом.

В сентябре 1932 года разведка Польши привлекает к разработке дешифратора «Энигмы» трех математиков, специалистов высшего класса – Мариана Режевского, Тадеуша Лисицкого и Генриха Зыгальского. В соответствии с их инструкциями польская фирма АВА воспроизводит 17 экземпляров немецкой шифровальной машины, а также отдельные ее части.

В декабре 1938 года после усовершенствования "Энигмы", Режевский, Лисицкий и Зыгальский делают огромные успехи: они создали настоящую счетную машину, предка ЭВМ, нареченную ими "Бомбой". Однако этим открытием экспозитура поделилась с французами лишь 30 июня 1939 года, за два месяца до начала войны.

В результате совместных усилий к марту 1940 года дешифровальные машины заработали на полную мощность. В Англии это был источник «Ультра» — эквивалент французскому «Зэд».

Немцы постоянно совершенствовали «Энигму». Операторов натаскивали на ее уничтожение в случае опасности. Ключи во время войны меняли каждые 8 часов. Шифродокументы растворялись в воде.

В Советском Союзе математики высокого класса были привлечены в криптографическую службу лишь в конце 40–х годов. В 1949 г. было создано Главное управление специальной связи (ГУСС) при ЦК КПСС.

На машинную шифросвязь в годы войны легла основная нагрузка при передаче секретных телеграмм: громоздкие М-100 заменили на более компактные М-101 («Изумруд»).

Широко использовалось и ручное шифрование. Телеграммы отправлялись с помощью легких, весом в три килограмма радиостанций «Север» выпускающихся в Ленинграде (Б. П. Асеев - инженер-конструктор, изобретатель, ученый). Уникальность радиостанции заключалась в ее портативности (масса приемопередатчика - около 2 кг), автономности питания и возможности работать в плавном диапазоне. Роль радиостанции «Север» в Великой Отечественной войне справедливо сравнивают с появлением в Красной Армии знаменитых ракетно-артиллерийских установок «Катюша».

2.3 Решение комбинаторных задач

Задача №1. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?

Решение.

1)    Выбираю из 6 женщин работника на 4 рабочих места женской специальности.

2)    Выбираю из 8 мужчин работника на 6 рабочих мест мужской специальности.

3)    После решения 1-ого и 2-ого пункта остаются 2 женщины и 2 мужчины на оставшиеся 3 вакансии, которые могут занять 4 человека не зависимо от пола.

4)    15*28*4=1680. Ответ: 1680 способов.

Задача № 2. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

Решение.

Все пассажиры должны ехать в разных вагонах, поэтому требуется отобрать 4 вагона из 9 с учетом порядка. Для решения задачи использую формулу размещения без повторения.

Ответ: 3024 способами можно рассадить в поезде 4 человека.

Задача №3. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

Решение.

Не менее 2-х человек, т.е 2+7 или 3+6 или 4+5 человек (5+4, 6+3, 7+2 – те же самые комбинации).

1)    Число выборок из 2-х человек

2)    Число выборок из 3-х человек

3)    Число выборок из 4-х человек

4)    Складываю результаты первых трех пунктов

Ответ: 246 способов.

3 Практическая часть

3.1 Анализ общих знаний комбинаторики

Для анализа общих знаний комбинаторики был проведен опрос студентов группы П-111 Белгородского правоохранительного колледжа имени Героя России В.В. Бурцева. В качестве способа коммуникации с респондентами было выбрано анкетирование. Анкета для опроса приведена в приложении А. В опросе участвовало 15 человек из них 6 девушек (40%) и 9 парней (60%). Среди опрошенных студентов 3 человека (20%) в 17-тилетнем возрасте, 1 человек, которому 15 лет, остальным 11 (73%) - 16 лет.

Ответы которые дали респонденты на вопросы о том какая оценка у них была в школе по математике и как они сами оценивают свои знания представлены в таблице 2.

Таблица 2 – Ответы на третий и четвертый вопрос анкеты

Пятым вопросом студентам было предложено из 3-х вариантов различных определений выбрать то, которое относится к комбинаторике. Результаты ответов представлены на рисунке 5.

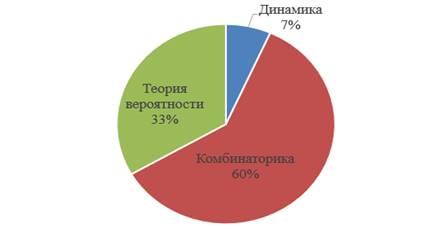
Рисунок 5 – Ответы студентов П-111 на пятый вопрос

В шестом вопросе респондентам были представлены четыре понятия и из этих понятий студентам необходимо было выбрать то которое относится к комбинаторике. Ответы на шестой вопрос представлены на рисунке 6, а определения всех понятий в таблице 3.

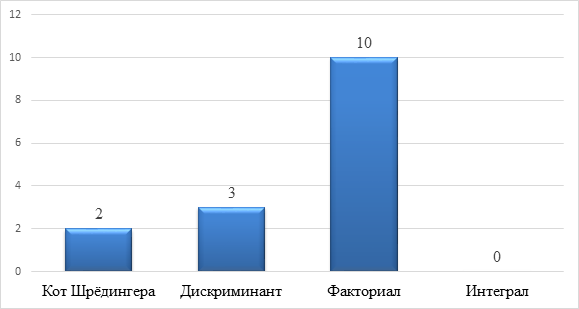
Рисунок 6 – Ответы на шестой вопрос

Таблица 3 – Определения понятий используемых в опросе

10 человек (67%) из предложенных формул выбрали формулу сочетания (), которая относится к комбинаторике. 3 респондента (20%) ответили  – периметр окружности, а двое выбрали формулу дискриминанта. Формулу корней квадратного уравнения () не выбрал ни один из респондентов.

60% опрошенных студентов смогли дать определение факториалу, 40% не смогли дать ответ.

На вопрос: При помощи какой формулы можно решить следующие задачи? (ответ можно записать формулой или написать что это сочетание, размещение или перестановка) полностью правильный ответ дали 6 человек (40%), 6 человек (40%) воздержались от ответа. Подробные результаты представлены на рисунке 7.

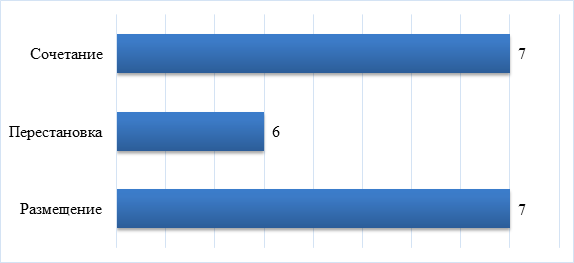
Рисунок 7 – Ответы на девятый вопрос

Пять студентов (33%) знают точные определения для размещения, перестановки и сочетания и дали точный ответ на десятый вопрос анкеты. 3 человека дали 2 правильных ответа из 3-х. 1 человек дал один правильный ответ из 3-х. Воздержались от ответа 6 человек (40%).

Из данных опроса видно, что большинство опрошенных имеют общее представление о комбинаторике и могут вычленить правильный ответ из предложенных вариантов, однако более глубокие знания, позволяющие решать комбинаторные задачи, лишь у 40% студентов.

3.2 Мероприятие на тему «Комбинаторика вокруг нас» в ходе просветительской деятельности

Исходя из данных полученных в ходе анализа общих знаний комбинаторики можно сделать вывод о необходимости проведения просветительских мероприятий на тему «Комбинаторика вокруг нас» среди студентов группы П-111 Белгородского правоохранительного колледжа имени Героя России В.В. Бурцева.

В ходе данной работы была подготовлена презентация в которой даны определения основным понятиям комбинаторики и рассмотрено применение комбинаторики в различных областях человеческой жизни.

Основная цель презентации на популярном уровне познакомить с разделом дискретной математики, который приобрел значимость в связи с развитием теории вероятностей, математической логики и информационных технологий. Студенты группы П-111 входе презентации должны получить представление о том, что такое комбинаторная задача, познакомиться с комбинаторным правилом умножения и систематическим перебором.

После презентации учащимся будет предложено решить 3 комбинаторные задачи, чтобы оценить эффективность проведенных мероприятий.

Заключение

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и получения законов распределения случайных величин. Это позволяет исследовать закономерности массовых случайных явлений, что важно для правильного понимания статистических закономерностей, проявляющихся в природе и технике. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни. Ее основы лежат в прикладном искусстве многих сфер деятельности человека. Комбинаторика используется в генетике, информатике, архитектуре, а также в различных играх (нарды, шашки, шахматы). В каждой из этих игр приходится рассматривать различные сочетания фигур, и выигрывает тот, кто их лучше изучает, знает выигрышные комбинации и умеет избегать проигрышных.

К шахматам можно относиться как к науке со своими законами и принципами. Шахматы содержат в себе элементы научного исследования – именно такой подход свойственен многим выдающимся шахматистам. Задачи, связанные с шахматной теорией, а именно с комбинаторикой, широко применяются в математике.

Основной способ поиска наилучшего хода заключается в переборе возможных ходов, рассмотрении движения по дереву последовательных позиций и оценке возникающих в результате них состояний игры. Играющему для подсчетов вариантов приходится тратить много времени даже в случае использования компьютера. Поэтому при поиске наиболее эффективных алгоритмов в компьютерных шахматах принято учитывать как можно больше ограничений (условий), упорядочивающих перебор, позволяющих отбрасывать те позиции, которые при выборе хода рассматривать не нужно. Эти задачи представляют из-за чего получили распространение эвристические методы их решения (метод перебора).

Впервые компьютерная шахматная программа  Deep Blue фирмы IBM обыграла чемпиона мира Каспарова при стандартном часовом контроле в 1996 году.

По существу компьютерные шахматы — едва ли не самый убедительный пример за полвека развития информационных технологий, когда именно в интеллектуальной деятельности автомат успешно соперничает с человеком.

В современном мире высоких технологий нас окружают всевозможные коды, которые управляют работой любого гаджета. Все компьютерные программы написаны с использованием двоичного кода. От расстановки единиц и нулей в коде зависит работа и назначение той или иной программы.

Даже если не рассматривать самый очевидный пример использования паролей и кодов, в нашей жизни коды встречаются повсеместно, начиная с даты нашего рождения.

Астрологи и нумерологи утверждают, что дата нашего рождения, это некий код, который откладывает отпечаток на наш характер и судьбу в целом.

Слова которыми мы пользуемся в обычной жизни можно тоже представить как коды, значение которых понятно всем. Но во время войны появилась необходимость шифровать послания так чтобы истинный смысл не был понятен врагу в случае перехвата послания. Для этого были придуманы всевозможные шифры, которые невозможно было взломать не разгадав код.

Ручные методы шифрования  занимали огромное количество времени и были недостаточно эффективны. Шифрование небольшого приказа занимало до 6 часов работы, примерно столько же требовалось на то, чтобы расшифровать полученное сообщение. Чтобы ускорить шифрование и дешифрование в годы второй мировой войны начали применять шифровальные машины (К-37 «Кристал», «Энигма вермахта», «Ультра», «Зэд», М-100, М-101 «Изумруд»).

Для анализа общих знаний комбинаторики был проведен опрос студентов группы П-111 Белгородского правоохранительного колледжа имени Героя России В.В. Бурцева. В качестве способа коммуникации с респондентами было выбрано анкетирование. В опросе участвовало 15 человек из них 6 девушек (40%) и 9 парней (60%). Среди опрошенных студентов 3 человека (20%) в 17-тилетнем возрасте, 1 человек, которому 15 лет, остальным 11 (73%) - 16 лет.

Из данных опроса видно, что большинство опрошенных имеют общее представление о комбинаторике и могут вычленить правильный ответ из предложенных вариантов, однако более глубокие знания, позволяющие решать комбинаторные задачи, лишь у 40% студентов.

Исходя из данных полученных в ходе анализа общих знаний комбинаторики можно сделать вывод о необходимости проведения просветительских мероприятий на тему «Комбинаторика вокруг нас» среди студентов группы П-111 Белгородского правоохранительного колледжа имени Героя России В.В. Бурцева.

В ходе данной работы была подготовлена презентация в которой даны определения основным понятиям комбинаторики и рассмотрено применение комбинаторики в различных областях человеческой жизни.

Можно сделать вывод, что дальнейшее развитие комбинаторики и теории вероятностей необходимо для научного прогресса, который ведет к улучшению уровня жизни населения, а, значит, к тому, к чему стремится все человечество на протяжении десятков веков.

Список использованных источников

Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. - М.: Просвещение, 2006.

Виленкин Н.Я. Популярная комбинаторика – М.: Наука, 1975.

Бродский Я. Об изучении элементов комбинаторики, вероятности, статистики в школе // Математика. – 2004. – № 31. – 2–8 с.

Гик Е.Я. Математика на шахматной доске. М.: Наука, 1976.

Глеман М., Варга Т. Вероятность в играх и развлечениях. Москва Просвещение 1979г.

Мордкович А. Г., Семенов П. В. События. Вероятности. Статистика. Дополнительные материалы к курсу алгебры для 7-9 классов. – М. 2002 г.

Окунев Л.Я. Комбинаторные задачи на шахматной доске. М.: Наука, 1985.

История шифровального дела, Т. Соболева, онлайн-читалка, http://coollib.net/b/175644/read.

Математический энциклопедический словарь http://bookre.org/reader?file=770058&pg=1

Приложение А

АНКЕТА МОНИТОРИНГОВОГО ИССЛЕДОВАНИЯ

АНАЛИЗ ОБЩИХ ЗНАНИЙ ПО КОМБИНАТОРИК

Уважаемые участники опроса! Внимательно ознакомьтесь с каждым вопросом анкеты, возможными вариантами ответов и ответьте на все из них, поставив галочку около соответствующего варианта или дайте свой ответ.

По результатам анкетирования будет произведен анализ общих знаний комбинаторики. Анкетирование проводится строго конфиденциально! Все полученные результаты будут использованы в обобщенном виде. Заполнение анкеты займет у вас 5-10 минут.

ЗАРАНЕЕ БЛАГОДАРИМ ВАС ЗА УЧАСТИЕ!