Учим правило "‘На меньше — делаем вычитание”.

— У Кати б красных шаров (выкладываем 6 красных кружков) и 4 синих (выкладываем внизу 4 синих кружка). На сколько у Кати красных шаров больше, чем синих?

— Как найдём на сколько больше красных шаров? (Нужно из красных отодвинуть столько, сколько синих, узнаем на сколько больше красных шаров.)

— Какое действие выберем? (Мы отодвинули шары, значит, действие “ вычитание”.)

ооооЬо

             •     •     •     •     I            7               6 — 4 = 2 (ш.)

Учим правило “Чтобы сравнить, на сколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее”.

— На ветке сидели птички. Когда 3 птички улетели (положите 3 палочки), то на ветке осталось ещё 5 птичек (положите отдельно ещё 5 палочек). Сколько птичек было на ветке сначала? Объясните, как нашли? Какое действие выберем?

3 + 5 = 8 (п.)

— В вазе стояло 7 цветов (положите 7 палочек). Среди них было 4 ромашки, а остальные васильки. Сколько в вазе было васильков? Как нашли? (Убрали 4 палочки, а остальные — это васильки.) Какое действие выберем? (Убрали — это действие

“вычитание”.)

7 - 4 = 3 (в.)

— У Димы было 6 конфет (положите б палочек.) После того, как он несколько конфет съел, у него осталось 2 конфеты.

На других примерах дети сами определяют, задача это или нет. Если нет, то поясняют почему и превращают в задачу, дополняя то, чего не хватает.

б) После того, как дети хорошо разберутся в понятии “задача”, будем учить их составлять задачи по картинкам, причём все виды задач.

— . . . Сколько всего яблок и груш?

— . . . На сколько яблок больше, чем груш?

— Яблок в вазе было 5 штук, а груш на 2 меньше. Сколько груш было в вазе?

После того, как задача составлена, надо выбрать нужное действие. Необходимо разъяснить детям смысл требования “решить задачу”. Решить задачу — это значит выбрать и выполнить нужное действие.

           в)                       Знакомить с элементами (с частями задачи) мы

будем тогда, когда дети научились составлять задачи и выбирать нужное действие.

— На опушке леса играли 3 зайчика, к ним выбежали ещё

2 зайчика. Сколько зайчиков стало на полянке?               ^

              — Что известно о зайчиках?             3     2                  Условие

               {Условие — это то, что известно в задаче.)             и_______

              — О чём нас спрашивают?               ?                    \

               {Вопрос — это то, что нужно найти.)I                                                                                                                        I W ,                       Т I                                        n j / T V n > - /              n w                                       r l i r i . /                             л_____________________

                    Какое действие выберем?            3 + 2 = 5           Решение

               {Решение — это выбранное нами действие.)           >_______

              — Сколько же стало зайчиков?                      5               Ответ

{Ответ — это найденное нами число.)

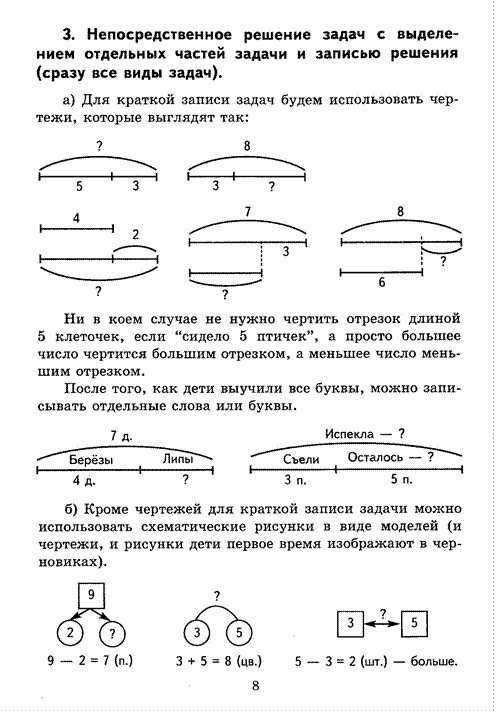
7 м.

2

             ?      5 м.

            7 - 5 = 2 (м.)                            6 + 2 = 8 (яб.)                         8 - 2 = 6 (к.)

Дети сами придумывают разные виды моделей к зарисовке задач.

в) Необходимо научить детей представлять то, о чём

говорится в задаче. Для этого на первых порах нужно увидеть (как по телевизору) зайчиков, которые бегают по полянке, или яблоки, которые мама положила в вазу и т. п.

г) С помощью опорных слов дети пока не смогут запи­

сывать задачи, так как им очень трудно выбрать главные слова из текста, но учитель должен использовать такую запись (вывешивая её на доске) для устного составления и решения задач. Многократное использование таких записей учителем приведет к тому, что впоследствии дети смогут сами оформлять запись задач.

4. Виды работ над простыми задачами (особое

внимание обратить на пункты щ з, и, к).

а) Составить задачу: по картинке, по чертежу, по схематическому рисунку, по краткой записи опорными словами, по решению.

б) Составить к данному условию вопрос или к вопросу

условие.

в) Изменить вопрос (или условие) так, чтобы задача

решалась другим действием.

г) Читаются задачи, а дети показывают знаки “+” или

(«_<<

д) Читаются задачи, а дети показывают только ответ (или записывают).

е) Читаются задачи, а дети записывают только ре­

шение.

ё) Решение задач в сравнении (одна решается письменно, другая устно, или ручкой другого цвета вносим

9

изменения в краткую запись задачи, а ниже этим же цветом записываем решение новой задачи).

— Саша поймал 4 рыбки, а Миша 3. На сколько больше поймал рыбок Саша?

— Саша поймал 4 рыбки, а Миша 3. Сколько всего рыбок поймали мальчики?

— В саду росло 6 кустов малины, а смородины на 3 куста больше (меньше). Сколько кустов смородины росло в саду?

ж) Решение задач с недостающими и лишними дан­

ными. Задачи такого вида приучают детей внимательнее анализировать содержание.

— Серёжа решил 7 примеров, а Ира решила больше примеров, чем Серёжа. Сколько примеров решила Ира?

— У Светы было 3 конфеты “Красная шапочка”, 2 конфеты “Мишка на Севере” и 5 конфет “Клубника со сливками”. Сколько всего шоколадных конфет было у Светы?

з) Решение “задач-вопросов”. Нужно как можно больше решать таких задач, так как они являются подготовкой к решению задач основного типа.

— Если известно сколько — Чтобы найти сколько шаров у Кати и известно на птиц осталось сидеть на ветсколько больше шаров у ке, что нужно знать?

         Тани, то что можно найти?                       _ Чтобы        узнать       на

— Если известно сколь- сколько больше красных ко машин уехало и известно шаров, чем синих, что нужно сколько осталось, то что знать?

        можно найти?                                                _ Чтобы найти сколько

— Если известно сколь- пирожков лежало на тарелке ко мама купила капусты и сначала, что нужно знать?

сколько моркови, то что можно найти?

и) Классификация задач (разделить задачи на группы по какому-то признаку или просто найти похожие задачи).

II. МЕТОДИКА РАБОТЫ НАД СОСТАВНЫМИ

ЗАДАЧАМИ В 1-м КЛАССЕ

1. Подготовительная работа.

а) Решение “задач-цепочек”.

— У Димы было 5 красных машин и 3 зелёные машины. Сколько всего машин было у Димы?

— У Димы было 8 машин, 2 машины он подарил другу. Сколько машин у него осталось?

— В вазе лежало 4 яблока, а груш на 2 больше. Сколько груш лежало в вазе?

— В вазе лежало 4 яблока и 6 груш. Сколько всего яблок и груш лежало в вазе?

(Вторая задача является продолжением первой.)

б) Решение задач с недостаюш;ими данными. В этих задачах нельзя ответить на вопрос задачи, так как неизвестно одно данное, точно так же как и в составных задачах.

в) Решение “задач-вопросов”.

— Чтобы найти сколько грибов было в двух корзинах, что нужно знать?

— Чтобы найти сколько птиц осталось сидеть на ветке, что нужно знать?

г) Решение задач с неопределёнными данными.

В клетку — / \ тетр.

                                                                 ^                    f ? тетр.

В линию — W тетр.

              д)                Знакомство со скобками необходимо, так как будем

решать задачи, составляя выражение.

2. Введение понятия “составная задача'’.

К этой теме можно переходить лишь тогда, когда научили детей хорошо решать все виды простых задач.

? шт.

Составьте и решите эти задачи (устно).

Есть ли что-то общее в этих задачах? (Вторая является продолжением первой.) Давайте составим из двух задач одну (один рассказ). Возьмём условие первой задачи, а вопрос от второй задачи (фигурная скобка из второй задачи переносится к первой).

— 5 шт.

? шт.

                                             —       на 2 шт. >

Дети составляют текст задачи. Эта задача называется составной. Почему? Кто догадался? (Её составили из двух задач.)

— Попробуем её решить. Можно ли сразу ответить на главный вопрос задачи, т. е. найти сколько всего ромашек и васильков было в букете (указкой показываем на “5" и на “?”), или пока нам что-то неизвестно? (Нам пока неизвестно сколько было васильков.)

— А можно ли найти сколько было васильков?

— Теперь мы знаем сколько было ромашек и сколько было васильков. Сможем ли мы теперь ответить на главный вопрос задачи (всё показываем по краткой записи)?

— Посмотрите, как будем записывать решение такой задачи:

1)  5 + 2 = 7 (шт.) — васильков.

2)  5 + 7 = 12 (шт.) — всего цветов.

Ответ. 12 цветов было в букете.

— Сравните решение этой задачи с решением тех задач, из которых мы её составили. Что вы заметили? (Первое действие — это решение первой задачи, а второе действие — это решение второй задачи.)

— Чем же будут отличаться новые задачи от тех, которые мы решали раньше? (Они будут решаться в два действия.)

— Да, дети. В составных задачах сразу нельзя ответить на главный вопрос задачи.

Эти задачи можно записать опорными словами или с помощью чертежа.

                                         ?______                                                5 м и 3 м

               ,^ ^ к о р .         ^                                                 I

                            б к.                на 2 к. <                                 4 м                    ?

3. Обучение решению задач путём составления выражения.

Не нужно решать задачу по действиям, а потом пытаться соединить все действия в одно выражение. Нужно научить детей рассуждать, отталкиваясь от вопроса задачи, и сразу составлять выражение.

На I полке — 7 кн.

На II полке — ?, на 4 кн. <.

После анализа текста и оформления краткой записи задачи закрываем листом часть задачи и задаём вопрос: “Чтобы найти сколько всего книг на двух полках, что нужно знать?” (Нужно знать сколько книг на первой полке и сколько книг на второй полке.)

На I полке

кн. На II полке

— и какое действие нужно выполнить? (Сложение.)

Ставим посередине строчки знак Опускаем лист вниз, открывая данные о первой полке.

— Сколько книг на I полке, нам известно? (Да, 7 книг.)

Пишем "7” слева от знака “+”. Опускаем лист ниже, открывая данные о второй полке.

— Сколько книг на II полке, мы знаем? (Нет.) Справа от знака “+” ставим скобки.

7  + (          ) =

Поднимаясь снизу вверх, записываем решение задачи по действиям или выражением.

1)  25 — 6 = 19 (м) — во II день.

2)  19 + 3 = 22 (м) — в III день.

3)  25 + 19 + 22 = 66 (м) — всего.

Задача. Во дворе играли 8 мальчиков и 6 девочек, из них 7 детей были школьниками. Сколько детей пока ещё не ходят в школу?

8  м и 6 д.

7 д.

(8 + 6) - 7 = 7 (д.)

5. Приёмы, способствующие формированию умения решать составные задачи.

а) Из двух простых задач составить одну задачу.

б) Из одной составной выделить несколько простых задач.

в) К условию придумать вопрос, чтобы задача реша­

лась в одно (два) действия.

г) К вопросу придумать условие, чтобы задача реша­

лась в одно (два) действия.

д) Составление задач по рисунку, схеме, чертежу, ре­

шению.

е) Решение задач в сравнении.

Наташа взяла в библиотеке 17 книг. 9 книг она уже прочитала. Сколько книг ей осталось прочитать?

На полянке росло 3 подосиновика и 2 груздя. Сколько всего грибов росло на полянке?

Наташа взяла в библиотеке 10 сказок и 7 книг о животных. 9 книг она уже прочитала. Сколько книг ей осталось прочитать?

На полянке росло 3 подосиновика, а груздей на 2 больше. Сколько всего грибов росло на полянке?

На трёх полках стояли книги. На первой полке было 11 книг, а на второй полке на 15 книг больше. Сколько книг стояло на трёх полках?

— Можно ли решить эту задачу?

— Измените условие так, чтобы можно было решить эту задачу.

— Поставьте вопросы к первоначальному условию, чтобы задачу можно было решить в одно действие (в 2 действия).

На уроках труда дети делали игрушки. Они сделали 10 зайчиков и 6 медвежат. Детскому саду они подарили 7 игрушек.

На сколько больше дети сделали зайчиков, чем медвежат?

— Все ли данные нужны для решения этой задачи?

— Измените условие, исключив лишние данные.

— Измените вопрос так, чтобы все данные были нужны для решения задачи.

л) Решение логических задач.

Один сосуд З^литровый, а другой 5“литровый. Как с помощью этих сосудов налить з кувшин 4 л воды из водопроводного крана?

На ветке сидело 5 синиц и 8 воробьёв, б птиц улетело. Улетел ли хоть один воробей?

Ребята стали спрашивать друг друга сколько кому лет.

Оказалось, что Митя младше Вани, но старше Пети. Ваня младше Бори, а Денис младше Пети. Кто из ребят старше всех? Кто младше всех?

          Младше всех                                                                     Старше всех

                           ■Д                 П                 М                 В

В трёх коробках лежат скрепки, кнопки и спички. Известно, что все три надписи — неверные. Определите, где что лежит.

          СКРЕПКИ                                  КНОПКИ                             НЕ СКРЕПКИ

III. МЕТОДИКА РАБОТЫ НАД ПРОСТЫМИ ЗАДАЧАМИ НА УМНОЖЕНИЕ И ДЕЛЕНИЕ

1. Подготовительная работа.

а) Для того, чтобы дети хорошо разобрались в смысле

команд возьмите по разложите по разложите на выполняем много практических упражнений с индивидуальным счётным материалом.

— Возьмите по 3 палочки 4 раза (выкладывают на партах). Сколько всего палочек вы взяли?

— Разложите 12 палочек по 3 палочки. Сколько кучек получилось? (Выясняем, как раскладывали.)

— Разложите 12 палочек на 3 равные части. Сколько палочек в каждой кучке? (Выясняем, как раскладывали.)

б) Затем решаем задачи (даётся текст задачи) практическим путём (используем счётные пешочки или зарисовываем схематические рисунки), решение пока не записываем, так как пока не вводили действий “умножение” и “деление”.

— По 4 яблока положили в 3 тарелки. Сколько всего яблок положили?

            оооо         оооо        о о о о

(Можно использовать действие сложение.) Ответ. 12 яблок.

— 6 тетрадей раздали 3 детям поровну. Сколько тетрадей дали каждому?

(Зарисовываем по одному.) Ответ. 2 тетради.

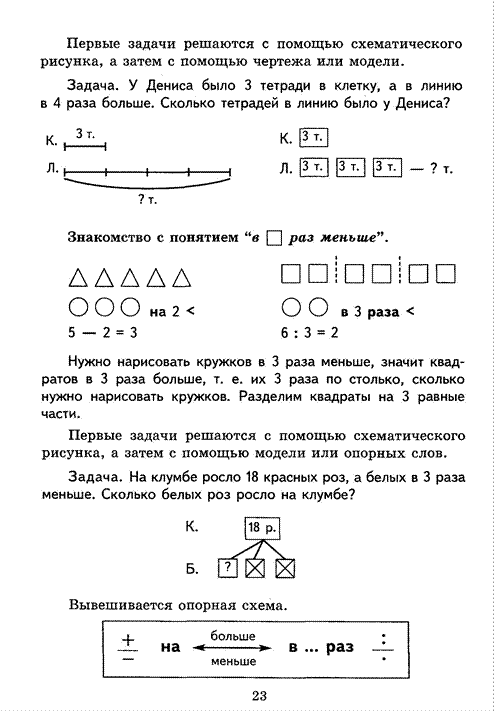
— Что обозначает число 4?

— Что обозначает число 2?

            4 р. 4 р.              — Что обозначает число 8?

После того, как дети усвоят эти понятия (через 1—2 урока), можно переходить к решению задач:

1   урок — на нахождение стоимости,

2   урок — на нахождение цены,3 урок — на нахождение количества.

Первые задачи каждого вида решаются на основе жизненных представлений (составляются формулы; следую- ш,ие задачи решаются на основе выученных правил). Это первые задачи, оформляемые в виде таблицы, поэтому нужно обратить на них внимание.

Задача. Каждая кукла стоит 5 рублей. Сколько стоят 3 таких куклы?

— На какие величины эта задача?

                                  Цена           Количество          Стоимость

                                  5 р.            Зк.                     ?р.

Заполнение таблицы идёт параллельно анализу текста задачи.

— Каждая кукла стоит 5 рублей. Что это за величина?

(Записываем под словом “цена”.)

— Сколько кукол купили? ... — Что это за величина?

— Что нужно найти? ... Что это за величина?

— Представьте, что вы в магазине. Как же найти, сколько нужно заплатить за 3 куклы?

                       5 • 3 = 15 (р.)         _{Ц • К = С}

Так же выводятся все другие формулы.

Необходимо научить детей составлять задачи по таблице (не перечислять известные и неизвестные величины, а составлять рассказ) и составлять обратные задачи.

— Я начну предложение, а вы должны его закончить. Если ткани взяли в 5 раз больше, то и рубашек сошьют ... (в 5 раз больше).

— Как же найти сколько сошьют рубашек, если вы сказали, что их сошьют в 5 раз больше?

Решение:

1) 50 :10 = 5 (раз) — больше возьмут ткани. 2) 3 • 5 = 15 (рубашек) — из 50 метров.

4.    Задачи на пропорциональное деление.

Подготовительная работа — решаются задачи упрощённого вида.

                Папа — 3 шок.           р        С I гр. — 2 ведра.

I50 кг

                Мама — 5 шок.                    Со II гр. — 3 ведра.,ра.]

                 Стоит 1 шок. — ? р.               Масса 1 ведра — ? кг.

Анализ решения;

— Дети, как находится цена?

— Посмотрите, какая стоимость известна в задаче? (...) — Можно сказать так: “Нам известна общая стоимость”.

— Если известна “общая” стоимость, то какое же нужно найти количество, как вы думаете? (Общее количество.)

— Теперь мы знаем “общую стоимость” и “общее количество”, что можно найти? (Цену шоколадки.)

Затем через несколько уроков вводятся задачи стандартного вида, при анализе решения которых выделяются понятия “обитая стоимость” (масса, расход, расстояние) и “общее количество”.

                                           Цена            Количество       Стоимость

                         1       одинаковая              5 м

^ 3 6 р.

                        II                                       7 м

— Можно ли сразу ответить на главные вопросы задачи (Нет, так как неизвестна цена.)

29

— Вспомним правило нахождения цены. (Ц = С : К) — Какая стоимость известна в задаче? (Общая стоимость.) — Если известна “общая” стоимость, то что нужно найти?

(Общее количество.)

— Зная общую стоимость и общее количество, что можно найти? (Цену.)

— Зная цену, можно ли ответить на вопросы задачи?

Для краткой записи этих задач можно использовать чертежи.

                            50 кг                                                              36 р.

                                 И гр.               ■                            Г                            и

    l-LLii:)-------1— —I---------------1---------1I —  --------- --------------------------1__- ---------- 1

                                                                               5м — ? р.             7м — ?р

      Подготовительные задачи.                    Задачи стандартного вида.

5.  Задачи на нахождение неизвестного по двум разностям.

Подготовительные упражнения:

а) Наташа купила 3 тетради, а Света 5 таких же тетрадей.

Кто из них больше заплатил денег?

— Почему?

— На сколько больше Света купила тетрадей?

— Слушайте дальше. Света купила на 2 тетради больше и поэтому заплатила на 8 рублей больше. Что можно узнать по этим данным?

— Сколько же за свои тетради заплатила Наташа? — Сколько за свои тетради заплатила Света?

б) В первый день в ателье сшили 5 костюмов, а во второй 8 таких же костюмов. В какой день израсходовали больше ткани?

— Почему?

— На сколько больше костюмов сшили во второй день?

— Слушайте дальше. Во второй день сшили на 3 костюма больше и поэтому израсходовали на 12 м ткани больше. Что можно найти по этим данным?

30

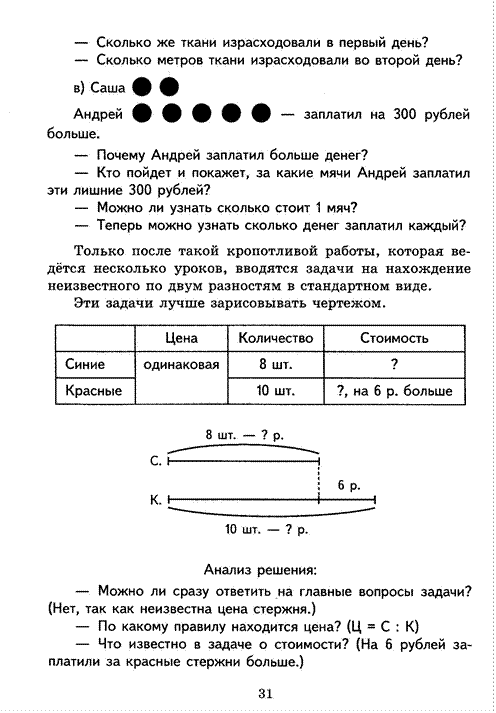
— Почему за красные стержни заплатили больше? (Потому что их больше купили.)

— Можно ли найти на сколько их больше купили? (Да,

10 — 8 = 2)

— Итак, Дима заплатил за красные стержни на 6 рублей больше, потому что он купил их на 2 больше. Что можно найти по этим данным? (Можно найти цену стержня.)

— Сможем ли мы теперь ответить на главные вопросы задачи?

6.    Задачи на движение.

На подготовительном этапе на основе движущихся моделей дети должны уяснить что значит двигаться навстречу друг другу и в противоположных направлениях. Необходимо познакомить детей с элементами чертежей к задачам на движение и научить их вычерчивать по условию задачи.

                                    24 м                                               ?, на 8 м <

{ м

После такого предварительного знакомства вводится понятие “скорость”. Беседа начинается с того, что есть предметы движущиеся и недвижущиеся (дети приводят примеры). Опираясь на жизненный опыт детей, выясняем, что одни предметы движутся быстрее, другие медленнее.

Открываем таблицу на доске;

             Пешеход — 5 км за 1 час                        5     км /ч

             Автомобиль — 80 км за 1 час            80 км /ч

              Ракета — 6 км за 1 сек.                           6     км /с

             Черепаха — 5 м за 1 мин.                         5 м/мин

32

в этом случае говорят, что скорость пешехода 5 км в час (показываем запись 5 км/ч) и т. д.

Скорость движения — это расстояние, которое проходит движущийся предмет за единицу времени (за 1 час, за 1 минуту, за 1 секунду).

— Проверим, как вы меня поняли. Скорость поезда 70 км/ч.

Что это означает? (Поезд проезжает 70 км за 1 час.) — Скорость мухи — 5 м /с — ?

— Скорость африканского страуса — 120 км /ч — ?

Задача. Велосипедист был в пути 3 ч и проехал за это время 36 км. В течение каждого часа он проезжал одинаковое расстояние. Сколько километров проезжал велосипедист в каждый час?

36 ч

Пояснить, что чёрточки означают количество часов.

36 : 3 = 12 (?)

Мы нашли, сколько километров проезжал велосипедист за каждый час, т. е. за 1 час или за единицу времени. Что же это за величина? (Скорость.) Как обозначим единицу измерения скорости? (км/ч)

                                                                                       S        t = V

36 : 3 = 12 (км/ч)

расст. вр. скор.

Вывешивается формула и заучивается правило.

На следующих уроках вводятся два других правила. После того, как дети выучат правила, задачи решаются в два и более действия; используется краткая запись в виде чертежа или таблицы.

Необходимо познакомить детей с понятием “обпдей скорости” (скорость сближения или удаления) и пояснить, что использование понятия “обитая скорость” упрош;ает решение задач.

2) Задача. Одна машина за один час может перевезти 15 т груза, а другая за 1 час может перевезти 20 т груза. Сколько времени им потребуется, чтобы перевезти 105 т груза, если они будут работать вместе?

Задача. Рукопись в 60 страниц машинистка может перепечатать за 10 часов, а ученица за 15 часов. За сколько часов они перепечатают рукопись, работая вместе?

В задачах этого вида детям трудно разобраться в содержании задачи, так как ни в одной другой задаче одно и то же число не использовалось для выполнения решения несколько раз. Поэтому в этих задачах необходимо очень кропотливо проводить анализ содержания задачи.

— О чём эта задача?

— Сколько часов нужно машинистке, чтобы перепечатать всю рукопись? (10 часов.)

— А сколько страниц рукописи она перепечатает за 10 часов? (60 страниц.)

— А сколько будет работать ученица? (15 часов.)

— А за 15 часов сколько страниц она перепечатает?

(60 страниц.)

— Если они будут работать вместе, то сколько им нужно перепечатать страниц? (60 страниц.) — Какой вопрос задачи?

Машинистка — 60 стр. за 10 ч.

Ученица — 60 стр. за 15 ч.

Вместе — 60 стр. за ? ч.

Такой вид краткой записи очень удобен для проведения анализа решения задачи.

В первых 2—3 задачах анализ решения лучше проводить от данных к вопросу, а в первой задаче анализ решения лучше вести с параллельной записью решения.

— Если ученица и машинистка будут работать вместе, то им потребуется времени больше или меньше, чем 10 часов?

— Что известно о машинистке? Что можно найти по этим данным?

V. виды РАБОТ С ТЕКСТОВЫМИ ЗАДАЧАМИ ПО РАЗВИВАЮЩЕМУ ОБУЧЕНИЮ

1. Работа над задачами с лишними данными.

1)              Из 24 м шёлка сшили 3 платья, 2 блузки и 2 халата. На блузки пошло 4 м шёлка, на платья — на 8 м больше, чем на блузки, а на халаты — остальной шёлк. Сколько метров шёлка пошло на халаты?

— Все ли числа понадобятся для решения?

— Измените условие задачи, чтобы в нём остались только те числа, которые необходимы для решения задачи.

— Какие вопросы можно поставить к первоначальному условию? (Сколько метров пошло на 1 халат? Сколько метров пошло на платье и на халат? На сколько метров больше пошло на 1 халат, чем на 1 блузку? ... )

2)              Турист проехал на автомашине 146 км, а на пароходе на

50 км меньше, чем на автомобиле. Пешком турист прошёл 12 км. Весь его путь составил 264 км. Сколько километров проехал турист на пароходе?

— Измените условие, чтобы остались только те данные, которые нужны для решения.

— Измените вопрос и условие, чтобы в задаче не было лишних данных.

3) В каждый прилёт к гнезду скворец несёт 3 саранчи, по 2 грамма каждая. В день пара скворцов прилетает к гнезду 40 раз. Сколько саранчи съедят птицы за день?

— Что вы заметили?

— Как нужно поставить вопрос, чтобы для решения задачи нужны были все данные числа?

2. Работа над задачами с недостающими данными.

Из двух городов выехали одновременно навстречу друг другу 2 мотоциклиста. Один мотоциклист двигался со ско­

8. Работа с текстом задачи.

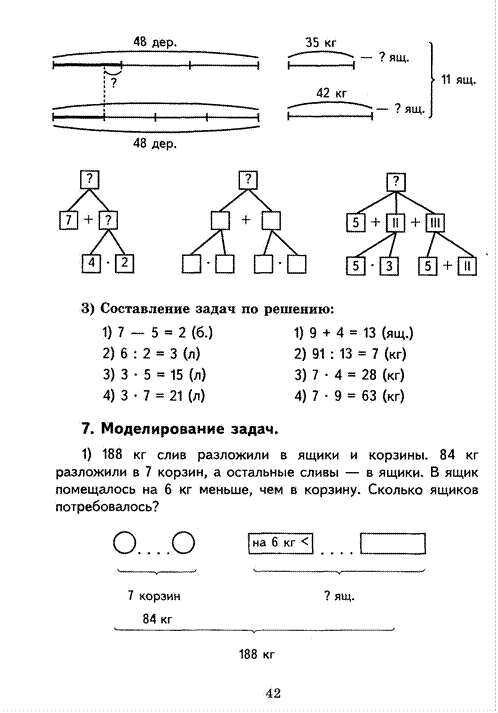
1)   Чип собрал 18 съедобных грибов и 9 поганок, Дейл собрал 6 съедобных грибов, а поганок на 5 больше, чем съедобных грибов. Сколько всего съедобных грибов принесли Чип и Дейл? Какие вопросы еще можно задать?

— Сколько поганок собрали Чип и Дейл?

— Сколько всего грибов собрали Чип и Дейл?

— Сколько грибов собрал Чип?

— Во сколько раз Чип собрал больше съедобных грибов, чем Дейл? и т. д.

                                                     Съедобные                   Поганки

                         Чип    I-------------------------------------1---------------------- 1

                                                          18 шт.                             9 шт.

                                         Съедобные           Поганки

Дейл I------------------ 1----------------------------1

                                                6 шт.                на 5 шт. >

2)   На расчистку дороги от снежных заносов из одного села пришли 173 человека, из второго в 2 раза больше, чем из первого, а из третьего — на 189 человек меньше, чем из второго.

— Составьте вопрос и решите задачу в 2 действия (в 3 действия).

— Составьте вопрос так, чтобы в условии оказались лишние данные.

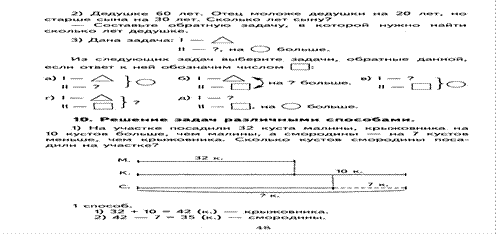
3)   Деду 68 лет, отец моложе его в 2 раза, а сын моложе отца на 23 года. Сколько лет сыну?

— Если изменить одно числовое данное — отец моложе деда в 3 раза, придётся ли изменить другие числовые данные?

4)   Три сборш,ика собрали 160 кг ягод шиповника. Первый собрал 63 кг, а первый и второй вместе 112 кг. Сколько килограммов ягод собрал второй сборщик и сколько третий?

— Какие числа в задаче окажутся лишними, если к её условию поставить такой вопрос: сколько килограммов шиповника собрал второй сборщик? (Сколько килограммов ягод собрал третий сборщик?)

Вопросы;

а) Во сколько раз израсходовали орехов меньше, чем

осталось?

б) Сколько килограммов орехов было во всех пакетах?

в) На сколько больше орехов осталось, чем израсхо­

довали?

г) Во сколько раз израсходовали пакетов меньше, чем

осталось?

д) Сколько килограммов орехов израсходовали?

е) Сколько килограммов орехов осталось?

          ё) На     сколько     больше     израсходовали     орехов,     чем

осталось?

8) Найди к каждому условию подходящий вопрос, запиши рядом их номера (условие, вопрос). Постарайся как можно

больше составить разных задач с данными условиями и вопросами. Реши составленные задачи.

Условия

1)                С одного участка со­брали 12 кг клубники в 4 одинаковые корзинки, а со второго на 6 кг клубники больше, чем с первого.

2)                С одного участка со­брали 24 кг клубники, а со второго на 18 кг больше, чем с первого.

3)                С одного участка со­брали 42 кг клубники, а со второго на 15 кг меньше. Всю клубнику разложили в корзинки, по 3 кг в каждую.

Вопросы

1)   Сколько килограммов клубники собрали с двух участков?

2)   Сколько корзинок по­надобилось для сбора клубники со второго участка?

3)   Сколько клубники со­брали со второго участка?

4)   На сколько больше корзинок понадобилось для сбора клубники со второго участка?

5)   Сколько корзинок по­надобилось для сбора клубники с двух участков?

6)   Во сколько раз боль­ше понадобилось корзинок для первого участка, чем для второго?

решения задач.

? л.

II          Осталось 7 л. в 2 раза >        6 л.

7 + 7 • 2 + 6 = 27 (л.)

27 л.

I-------------1---------------^II ,^{Осталось}

       7 л.       в 2 раза >

1 + 1 - 2 + х = 11

27 л.

I                          Осталось

Ч--------

?          в 2 раза >      6 л.

j: + x - 2+ 6 = 27

27 л.

I                         Осталось^

+ 7 л.      в ? раз >          6 л.

7 + 7 • X + 6 = 27

в) Мастер за 8 часов обработал 96 деталей. Сколько

деталей обработал мастер за 1 час?

г) Шесть мальчиков разделили между собой 90 орехов

поровну. Сколько орехов получил каждый из них?

д) К чаю подали 3 тарелки с пирожками, по 5 пирожков

на каждой. Сколько пирожков подали к чаю?

е) На машине привезли 600 кг картофеля, по 50 кг в каж­

дом мешке. Сколько мешков картофеля привезли?

ё) За тетради заплатили 60 рублей. Каждая тетрадь стоит 5 рублей. Сколько тетрадей купили?

ж) В мастерской из 62 м ткани сшили костюмы, расходуя

на каждый по 4 м. Сколько костюмов сшили в мастерской?

Теперь задачи в), г), е), ё), ж) — они все попали в одну группу, разбейте ещ,ё на 2 группы.

2) Разбейте данные задачи на 3 группы по сходству решений:

а) В детский сад привезли картофель. После того как на

протяжении 7 дней использовали по 13 кг картофеля еже­

дневно, его осталось 45 кг. Сколько картофеля привезли в детский сад?

б) Мама сделала 5 бутылок вишнёвого сока, а яблочного

в 2 раза больше. Сколько всего бутылок сока сделала мама?

в) Купили 2 баночки клея по 18 копеек и 12 тетрадей по 6 копеек. Сколько всего уплатили за покупку?

г) Масса дыни 3 кг, а масса тыквы в 4 раза больше. Какова

масса дыни и тыквы вместе?

д) В ателье сшили 15 платьев, расходуя на каждое платье по 3 метра. После этого в ателье осталось 40 метров ткани.

Сколько всего метров ткани было в ателье?

е) В городском парке дети посадили 5 рядов берёз, по 7 берёз в каждом ряду, и 4 ряда клёнов, по 6 штук в каждом ряду. Сколько всего деревьев посадили ребята?

— К каждой группе задач придумайте ещё по одной.

з) Чем похожи эти задачи?

а) За 8 часов рабочий изготовил 56 деталей. Сколько деталей он изготовил за 5 часов?

50

б) 5 открыток стоят 30 копеек. Сколько стоят 15 таких же

открыток?

в) Автомобиль проехал 280 км за 7 часов. Сколько часов

ему потребуется, чтобы проехать 560 км, если он будет двигаться с той же скоростью?

г) Масса 3 коробок с яблоками 150 км. Найдите массу 7 та­

ких же коробок с яблоками.

д) Катя заплатила 96 копеек за 8 одинаковых шаров. Сколько таких же шаров она может купить на 60 копеек?

Но в этих задачах есть и отличия. Разбейте эти задачи на 2 группы.

I группа: а), б), г). II группа: в), д). Или I группа: а), г), д). II группа: б), в).

4) Разбейте эти задачи по две, чтобы из них можно было составить одну задачу.

а) На уроках труда ученики сшили 7 зайчиков и 5 мишек. Сколько всего игрушек сшили ученики?

б) Первая бригада собрала 15 т огурцов, а вторая в 2 раза

больше. Сколько всего тонн огурцов собрали рабочие?

в) У Светы было 18 конфет, она съела 6 конфет. Сколько

конфет у неё осталось?

г) Ученики сшили 12 игрушек и раздали в группы садика, каждой группе по 4 игрушке. Сколько групп получили игрушки?

д) Рабочие собрали 45 т огурцов и погрузили их на 9 ма­

шин поровну. Сколько тонн увезла каждая машина?

е) У Светы было 9 конфет, она раздала их трём своим

подругам поровну. Сколько конфет она дала каждой из своих подруг?

12. Логические задачи.

1)              В доме живут 13 ребят. Все они учатся в одной школе В школе всего 12 классов. Докажите, что хотя бы в одном классе есть двое учеников из этого дома.

2)              В корзине лежат яблоки двух сортов. Сколько нужно

51

вынуть из неё яблок, не заглядывая в корзину, чтобы среди них

оказалось хотя бы 2 яблока одного сорта?

3)              Гриша, Ваня и Коля живут в одном доме. Один из них блондин, другой брюнет, а третий русый. Узнай, каков цвет волос у каждого из них, если известно, что Гриша дружит с брюнетом; русый и Ваня учатся в одном классе; Коля пригласил на свой день рождения Гришу и блондина.

4)              На складе находилось 7 полных бочонков мёда, 7 напо­ловину заполненных мёдом, и 7 пустых бочонков. Как распределить все бочки между тремя покупателями так, чтобы каждый получил одинаковое количество мёда и бочонков?

5)              Имеются песочные часы на 3 минуты и 7 минут. Надо опустить яйцо ровно на 4 минуты в кипящую воду. Как это сделать с помощью этих часов?

6)              Один рыбак поймал за 2 часа 8 карасей. Сколько карасей поймают 3 рыбака за 3 часа?

13. Решение задач повышенной сложности.

1)              Помидоры укладывали в одинаковые ящики. В 7 ящиках помещается на 32 кг больше, чем в трёх. Хватит ли для укладки 872 кг помидоров 120 ящиков?

2)              В трёх кусках было 127 м шпагата. Когда от первого отрезали 21 м, от второго 9 м, а от третьего 7 м, то во всех кусках осталось поровну. Сколько метров шпагата было в каж­

дом куске?

3)              В два автобуса сели 123 туриста. Затем из одного авто­буса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали в машине. После этого туристов в автобусах стало поровну. Сколько их было в автобусе сначала?

4)              Два поезда идут навстречу друг другу с двух станций, расстояние между которыми 385 км. Первый поезд вышел раньше на 2 часа и двигался со скоростью 53 км/ч. Через 3 часа после выхода второго поезда они встретились. Найти скорость второго поезда.

52

5) Для пополнения школьной библиотеки нужно было 66 книг. Сначала купили 40 книг, которые были упакованы в 5 одинаковых пачек, а потом ещё 3 такие же пачки. Хватит ли всех купленных книг для пополнения библиотеки?

Анализ решения задачи № 4 от вопроса к данным.

             53 км /ч         53 км /ч                                    ^                            ? км /ч

Н-------h

385 км

— Что нужно знать, чтобы найти скорость второго поезда?

(Расстояние, пройденное им, и время его движения.)

— Что из этих величин известно, а что нет? (Время известно — 3 часа, а расстояние — нет.)

— Что нужно знать, чтобы найти расстояние, пройденное вторым поездом? (Нужно знать всё расстояние и расстояние, пройденное первым поездом. Всё расстояние известно, а расстояние, пройденное первым поездом, неизвестно.)

— Что нужно знать, чтобы найти расстояние, пройденное первым поездом? (Нужно знать его скорость и время движения.

Скорость движения известна — 53 км/ч, а время — нет.)

— Что нужно знать, чтобы найти время движения первого поезда? (Нужно знать сколько часов он ехал один и сколько часов он ехал вместе с другим поездом. И то, и другое известно, значит, можно найти время, которое был в пути первый поезд, сложением (2 + 3).)

Рассуждая в обратном порядке, записываем решение задачи.

Анализ решения задачи № 5 от данных к вопросу.

— Найдите два данных, по которым можно что-то найти. (40 книг были упакованы в 5 одинаковых пачек. Можно найти сколько книг в одной пачке — делением.)

— Найдите ещё два данных, по которым можно что-то найти. (Теперь известно сколько книг в одной пачке и известно,

53

СОДЕРЖАНИЕ

I. МЕТОДИКА РАБОТЫ НАД ПРОСТЫМИ ЗАДАЧАМИ

НА СЛОЖЕНИЕ И ВЫЧИТАНИЕ..............................................................3

1.   Подготовительная работа        .......................................................3

2.   Формирование представления о задаче .............................6 3. Непосредственное решение задач с выделением отдельных частей задачи и с записью решения.....................8

4. Виды работ над простыми задачами...................................9

П. МЕТОДИКА РАБОТЫ НАД СОСТАВНЫМИ ЗАДАЧАМИ

В 1-м КЛАССЕ....................................................................................................10

1.   Подготовительная работа...................................................12

2.   Введение понятия “составная задача” ..........................12 3. Обучение решению задач путём составления

выражения..................................................................................14

4.   Использование чертежей и блок-схем

при решении составных задач ............................................. 15

5.   Приёмы, способствующие формированию

умения решать составные задачи ........................................16

Ш. МЕТОДИКА РАБОТЫ НАД ПРОСТЫМИ ЗАДАЧАМИ

НА УМНОЖЕНИЕ И ДЕЛЕНИЕ.................................................................... 20

1.   Подготовительная работа...................................................20

2.   Решение задач, раскрывающих смысл

умножения и деления..............................................................21

3.   Задачи на увеличение или уменьшение числа

в несколько р а з .............................................................................22 4. Задачи на кратное сравнение чисел.................................. 24

IV. МЕТОДИКА РАБОТЫ НАД ЗАДАЧАМИ

НА ВЗАИМОСВЯЗЬ ВЕЛИЧИН          ....................................................................25

1.   Задачи, раскрывающие взаимосвязь

между величинами.......................................................................25

2.   Задачи на нахождение четвёртого пропорционального . 26 3. Задачи на нахождение четвёртого

пропорционального способом отношений .............................28

4. Задачи на пропорциональное деление................................ 29

5. Задачи на нахождение неизвестногопо двум разностям....... 30

6. Задачи на движение........................................................... 32

7. Задачи на совместную работу..............................................34

62