КИМ по дисциплине "Дискретная математика"

ЕЙСКИЙ МОРСКОЙ РЫБОПРОМЫШЛЕННЫЙ ТЕХНИКУМ (ФИЛИАЛ)

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО
ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ
«АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

 

 

 

РАССМОТРЕНО на заседании цикловой комиссии математических дисциплин и информационных технологий Протокол № ____ Председатель_________ Е.В.Кодаченко  « 30» ____августа 2019 г.

УТВЕРЖДАЮ Заместитель директора по учебной работе __________ Е.Н.Горбанева  « 30» ____августа  2019г.

 

 

 

 

 

 

ПАСПОРТ

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ

 

УЧЕБНОЙ ДИСЦИПЛИНЫ

 

ОП.08 Дискретная математика

программы подготовки специалистов среднего звена (ППССЗ)

по специальности СПО

09.02.01 Компьютерные системы и комплексы

 (базовая подготовка)

 

 

 

 

 

 

 

 

 

2019

 

 

Разработчик:

 

 

 

1.Паспорт контрольно-измерительных материалов

               В соответствии с ФГОС СПО по специальности 35.02.09 Ихтиология и рыбоводство (углубленная подготовка) в процессе обучения по дисциплине ОП. 09 Основы алгоритмизации и программирования, у обучающегося формируются  следующие общие компетенции (ОК):

 

OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

 

следующие профессиональные компетенции (ПК):

ПК 1.1.Разрабатывать схемы цифровых устройств на основе интегральных схем разной степени интеграции.

ПК 1.3. Использовать средства и методы автоматизированного проектирования при разработке цифровых устройств.

 

С целью овладения формирования вышеуказанных компетенций обучающийся в ходе освоения дисциплины  должен:

уметь:

У1- формулировать задачи логического характера и применять средства математической логики для их решения;

У2-применять законы алгебры логики;

У3- определять типы графов и давать их характеристики;

У4-строить простейшие автоматы;

Знать:

З1-основные понятия и приемы дискретной математики;

З2-логические операции, формулы логики, законы алгебры логики;

З3-основные классы функций, полноту множества функций, теорему Поста;

З4-основные понятия теории множеств, теоретико-множественные операции и их связь с логическими операциями;

З5-логика предикатов, бинарные отношения и их виды;

З6-элементы теории отображений и алгебры подстановок;

З7-метод математической индукции;

З8-алгоритмическое перечисление основных комбинаторных объектов;

З9-основные понятия теории графов, характеристики и виды графов;

З10-элементы теории автоматов.

2. Результаты освоения профессиональных компетенций (ПК), соответствующих виду профессиональной деятельности, и элементов общих компетенций (ОК) текущим контролем и промежуточной аттестацией:

 

Результаты (освоенные общие компетенции)	Основные показатели оценки результата	Формы и методы контроля и оценки
1	2	3
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.	Проявлять устойчивый интерес к будущей профессии.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических занятий, внеаудиторной самостоятельной работы. Наблюдение и оценка активности обучающегося при проведении учебно-воспитательных мероприятий профессиональной направленности (конкурсы на лучшего знатока дисциплины, участие в мероприятиях недели цикловой комиссии, профессиональные конкурсы, «брейн-ринги» и т. п.).
ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.	Мотивированная обоснованность выбора и применения методов и способов решения профессиональных задач; своевременность, правильность и полнота выполнения профессиональных задач.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических занятий, внеаудиторной самостоятельной работы.
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.	Способность принимать решения в стандартных и нестандартных  ситуациях и нести за них ответственность при выполнении профессиональных задач.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических  занятий, внеаудиторной самостоятельной работы.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.	Оперативность поиска и использования необходимой информации для качественного выполнения профессиональных задач, профессионального и личностного развития; широта использования различных источников информации, включая электронные.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических  занятий, внеаудиторной самостоятельной работы.
ОК 5. Использовать информационно - коммуникационные технологии для совершенствования профессиональной деятельности.	Выполнение и демонстрация компьютерной обработки полученных результатов в профессиональной деятельности	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении внеаудиторной самостоятельной работы.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями	Коммуникабельность при взаимодействии с обучающимися, преподавателями практики в процессе обучения.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических  занятий, внеаудиторной самостоятельной работы. Наблюдение и оценка использования обучающимся коммуникативных методов и приемов при подготовке и проведении учебно-воспитательных мероприятий различной тематики.
ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполненных заданий.	Ответственность за результат выполнения заданий; способность к самоанализу и коррекции результатов собственной работы.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических  занятий. Наблюдение и оценка уровня ответственности обучающегося за работу членов команды, при проведении учебно-воспитательных мероприятий различной тематики, общественной деятельности.
ОК 8. Самостоятельно определять задачи про- фессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.	Способность: планировать и организовывать задачи про- фессионального и личностного развития; заниматься самообразованием и осознанно планировать повышение квалификации.	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении и  практических  занятий, внеаудиторной самостоятельной работы.
ОК 9. Быть готовым к смене технологий в профессиональной деятельности.	Проявление интереса к инновациям в области профессиональной деятельности	Оценка деятельности обучающегося в процессе освоения образовательной программы осуществляется  при проведении теоретических занятий, выполнении практических  занятий, внеаудиторной самостоятельной работы.

 

 

 

Вид профессиональной деятельности (ВПД)	ПК	ОПОР	У	З	Формы и методы контроля и оценки
Проектирование цифровых устройств	ПК 1.1. Разрабатывать схемы цифровых устройств на основе интегральных схем разной степени интеграции.	1.1.1 Изложение арифметических и логических основ цифровой техники	У1,  у3	З5-З 10	Текущий контроль практические занятия, контрольная работа, письменная работа, устный опрос, тестирование, диктант. Промежуточная аттестация экзамен
	ПК 1.3. Использовать средства и методы автоматизированного проектирования при разработке цифровых устройств.	1.3.1 Изложение особенностей применения систем автоматизированного проектирования, пакетов прикладных программ	У2, У4	З1-З4

3. Формы и методы оценивания дисциплины

Предметом оценки служат умения и знания, формирующие профессиональные компетенции, а также способствующие развитию общих компетенций по ОП. 08 Дискретная математика 09.02.01 Компьютерные системы и комплексы

 

Содержательно-компетентностная матрица оценочных средств текущего контроля.

 

Содержание учебного материала по программе УД	ПК 1.1		ОК
	У 1- У4	З1-З10
Раздел 1 Ведение в дискретную математику
Тема 1.1 Введение, основное содержание и цели изучения предмета дискретная математика
Раздел 2 Множества
Тема 2.1 Основные понятия и определения теории множеств. Операции над множествами
Тема 2.2 Упорядоченные множества
Тема 2.3 Соответствия и отображения
Раздел 3 Теория графов
Тема 3.1 Введение в теорию графов
Тема 3.2 Различные графы
Тема 3.3. Алгоритмы обхода графов. Транспортные сети
Раздел 4 Математическая логика
Тема 4.1 Алгебра логики
Тема 4.2 Законы логики Равносильные преобразования
Раздел 5 Булевы функции
Тема 5.1 Функции алгебры логики
Тема 5.2 Операция двоичного сложения. Многочлен Жегалкина
Тема 5.3 Полнота множества функций. Важнейшие замкнутые классы. Теорема Поста
Тема 5.4 Метод математической индукции
Раздел 6 Предикаты. Бинарные отношения
Тема 6.1 Предикаты
Тема 6.2 Бинарные отношения
Раздел 7 Элементы теории автоматов
Тема 7.1 Введение в теорию автоматов
Тема 7.2 Логические конечные автоматы. Схемы алгоритмов и потоков

Примечание: уо-устный опрос; пр – письменная работа; д-диктант; т- тестирование; лр – лабораторная работа; пз– практическое занятие; ср – самостоятельная работа (внеаудиторная); КР-курсовая работа

Содержательно-компетентностная матрица оценочных средств промежуточной аттестации.

Содержание учебного материала по программе УД	ПК 2.1
	У 1- У4	З1-З10
Раздел 1 Ведение в дискретную математику
Тема 1.1 Введение, основное содержание и цели изучения предмета дискретная математика
Раздел 2 Множества
Тема 2.1 Основные понятия и определения теории множеств. Операции над множествами
Тема 2.2 Упорядоченные множества
Тема 2.3 Соответствия и отображения
Раздел 3 Теория графов
Тема 3.1 Введение в теорию графов
Тема 3.2 Различные графы
Тема 3.3. Алгоритмы обхода графов. Транспортные сети
Раздел 4 Математическая логика
Тема 4.1 Алгебра логики
Тема 4.2 Законы логики Равносильные преобразования
Раздел 5 Булевы функции
Тема 5.1 Функции алгебры логики
Тема 5.2 Операция двоичного сложения. Многочлен Жегалкина
Тема 5.3 Полнота множества функций. Важнейшие замкнутые классы. Теорема Поста
Тема 5.4 Метод математической индукции
Раздел 6 Предикаты. Бинарные отношения
Тема 6.1 Предикаты
Тема 6.2 Бинарные отношения
Раздел 7 Элементы теории автоматов
Тема 7.1 Введение в теорию автоматов
Тема 7.2 Логические конечные автоматы. Схемы алгоритмов и потоков

 

Примечание: дз – дифференцированный зачет; э - экзамен

4. Задания для оценки освоения профессионального модуля

4.1 Задания текущего контроля

 

Раздел 1 Ведение в дискретную математику

Тема 1.1 Введение, основное содержание и цели изучения предмета дискретная математика

Самостоятельная (внеаудиторная) работа

Найти материал по теме «Основоположники дискретной математики»

 

Раздел 2 Множества

Тема 2.1 Основные понятия и определения теории множеств. Операции над множествами

Устный опрос

-        Деление математики на классическую и дискретную. История дискретной математики.

-        Основные разделы курса. Некоторые общепринятые обозначения.

Самостоятельная (внеаудиторная) работа

Найти материал по теме: «бинарные и тернарные отношения», отчёт по практическому  занятию №1

Практическое занятие № 1

Решение задач по темам: операции над множествами, сравнение множеств, разбиения и покрытия. Прямое произведение множеств. Отношения эквивалентности

1.                    Вопросы и упражнения для самопроверки. Ответы оформите в тетради

2.     Вставьте обозначения числовых множеств:

- множество натуральных чисел;

множество целых чисел;

множество рациональных чисел;

множество действительных чисел.

3.     Вставьте пропущенный знак е или g: 117_____ Ʌ ; 22,4     Z;         4/3       Q;

V2_____ Q; V75________ R; ʌ __________ Z.

4.     Принадлежит ли множеству корней уравнения х² - 5х+6 = о число х = -3 ?

5.     Какими способами можно задать множество?

6.     Запишите множество действительных корней уравнения 3х+4 = 0. Как записать ответ, если требуется найти множество целых корней этого уравнения?

7.     Что такое подмножество данного множества? Какой символ

используется для записи “множествоА является подмножеством множества 5”? Запишите его: А         В.

8.     Вставьте пропущенный символ е или с:

 

9.     Обведите кружком номер правильного ответа:

Множество всех элементов, принадлежащих как множеству А, так и множеству В, называется:

1)    объединением множествА и В;

2)    пересечением множествА и В;

3)    разностью множествА и В.

10. Вставьте пропущенные знаки операций над множествами:

{a,b, c}        {d, b, e} = {b};

{a, b, c}       {c, d} = {a, b, c, d};

{a, b, c}       {a, d} = {b, c} .

11. Что такое булеан множества Х?

12.  Является ли булеаном множества {a, ь, с}система подмножеств

{{a},{b},{c}} ?

13. Является ли разбиением множества {а,ь,с} система подмножеств {{a, b},{b, c},{a, с}} ? Является ли она покрытием данного множества?

14. Нарисуйте диаграмму Эйлера - Венна для множества aʌ (bи с). Нарисуйте диаграмму для (aʌ B) и (aʌ C). Сравните заштрихованную часть на обеих диаграммах. Как называется закон, который Вы проиллюстрировали?

15. Нарисуйте диаграммы Эйлера - Венна для левой и правой частей закона де Моргана. Сравните их.

16. Запишите законы алгебры множеств. Запомните их названия.

1.    Решение задач

Д и а г р а м м ы Э й л е р а - В е н н а.

1.     Четырнадцать спортсменов участвовали в кроссе, 16 - в соревнованиях по плаванию, 10 - в велосипедных гонках. Восемь участников участвовали в кроссе и заплыве, 4 - в кроссе и велосипедных гонках, 9 - в плавании и велосипедных гонках. Во всех трех соревнованиях участвовали три человека. Сколько всего было спортсменов?

2.     В туристском клубе несколько раз за лето организуются походы, причем все члены клуба хотя бы раз в них участвуют. Сорок человек побывали в пеших походах, 28 - в конных, 25 - в лодочных.И в пеших, и в конных походах побывало 20 человек, в пеших и лодочных - 15, в конных и лодочных - 8, во всех видах походов побывало 6 человек. Сколько туристов в клубе?

3.     В отделе НИИ работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. Английский язык знают шесть человек, немецкий - шесть человек, французский - семь. Четыре человека знают английский и немецкий языки, три человека - немецкий и французский, два - французский и английский, один знает все три языка. Сколько человек работает в отделе?

4.     Из 80 студентов занимаются баскетболом 30 человек, легкой атлетикой 25 человек, шахматами - 40 человек. Баскетболом и легкой атлетикой занимается 8 человек, шахматами и легкой атлетикой - 10 человек, шахматами и баскетболом - 5 человек. Тремя видами спорта занимаются три человека. Сколько человек занимаются спортом?

5.     Десять читателей взяли в библиотеке фантастику, 11 - детективы, 8 - приключения. Фантастику и приключения взяли 4 человека, фантастику и детективы - 6, приключения и детективы - 3, двое взяли три вида книг. Сколько читателей побывало в библиотеке?

 

Тема 2.2 Упорядоченные множества

Работа с карточками

Вариант 1 1.                 Понятие множеств. Приведите примеры 2.                 Симметрическая разность: обозначение, словесное описание, диаграмма Эйлера, символическая запись операции 3.                 Выполните действия и определите мощность полученного множества В= 4.                 Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующее множество и изобразите его кругами Эйлера:

Вариант 4 1.                 Изображение множеств. Подмножества. Приведите примеры 2.                 Объединение множеств: обозначение, словесное описание, диаграмма Эйлера, символическая запись операции 3.                 Выполните действия и определите мощность полученного множества 4.                 Даны отрезки А = [-7; 3], B = [1; 5], C = [4; 10]. Найдите следующие множества и изобразите их кругами Эйлера: ;

Вариант 2 1.                 Универсальные множества, Приведите примеры 2.                 Пересечение множеств: обозначение, словесное описание, диаграмма Эйлера, символическая запись операции 3.                 Выполните действия и определите мощность полученного множества 4.                 Даны отрезки А = [-2; 4], B = [2; 6], C = [5; 10]. Найдите следующие множества и изобразите их кругами Эйлера: ;

Вариант 5 1.     Язык теории множеств. Объясните значение  символов:Î, ", $,  D,  Ì,  Ï,  \ , ,  , Ø 2.                 Дополнение к множеству: обозначение, словесное описание, диаграмма Эйлера, символическая запись операции 3.                 Выполните действия и определите мощность полученного множества 4.                 Даны отрезки А = [-2; 4], B = [2; 6], C = [5; 10]. Найдите следующие множества и изобразите их кругами Эйлера: 5.

-        .

Самостоятельная (внеаудиторная) работа

Решение тестов по теме: «проверка теоретико-множественных соотношений с помощью формул логики», отчёт по практическому  занятию №2

Практическое занятие № 2

Решение задач на выполнение теоретико-множественных операций и на подсчет количества элементов с использованием формулы количества элементов в объединении нескольких конечных множеств

а)            Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующие множества и изобразите их кругами Эйлера:;

б)            ;

в)            ;

г)            .

1. Выполните действия и определите мощность полученного множества:

а)           

б)           

в)           

2. Решите задачу с помощью кругов Эйлера- Венна:

 Из 100 студентов факультета программирования 42 посещают спортивные секции, 30 – занятия НСО, а 28 – кружки художественной самодеятельности. На занятия НСО и спортом успевают ходить 5 студентов, спортом и художественной самодеятельностью занимаются 10, НСО и художественной самодеятельностью – 8, а сразу все три увлечения имеют три студента. Сколько студентов не посещают ни одно объединение по интересам, сколько занимаются чем-либо одним?

3. Самостоятельная работа. Выполните упражнения №1.19, 1.20, 1.21 стр.65 из учебника [1] по вариантам. Вариант  определяет преподаватель.

	1.19	1.20	1.21
Вариант 1	в	д	е
Вариант 2	г	е	д
Вариант 3	д	в	г
Вариант 4	е	г	в

 

Тема 2.3 Соответствия и отображения

Контрольная работа № 1 по теме «Множества».

I вариант

1.        Изобразите все операции над множествами с помощью кругов Эйлера и в символьном виде.

2.        Известно, что Х  ⋳ А ⋂ В. Следует ли отсюда, что   Х ⋳ А.

3.        Изобразите при помощи кругов Эйлера  а)  B⋂ C⋃A ;   б)  C \ B ⋂ A

4.        Найдите  А⋂ В ⋂ А ⋃  В, если:

1) А = {3; 4;5;6;7}           В = {3; 5;7;9}

2) А = {a, в, с, d, k}         В = {в, с, d}

3) А = {8; 9;10}               В = {7; 5; 6}

5.        Найдите объединение  множества решений неравенств, в которых переменная x - действительное число   -2 < х < 4  и  х ≥ -1   

6.        Используя круги Эйлера, проиллюстрируйте справедливость распределительного закона пересечения и объединения множеств.

7.        Запишите переместительный закон пересечения и объединения множеств.

8.        Найдите  А⋃ В ⋂ А \  В, если А = {-1; 0; 2; 4} В = [-2; 2].

 

 

Контрольная работа № 1 по теме «Множества».

II вариант

1.

1.        Понятие множества, способы описания множеств, основ.символы используемые в теории множества(пишем символ – обозначение)

2.        Известно, что Х ⋳ А⋃В. Следует ли отсюда, что   Х⋳ А⋂В

3.         Изобразите при помощи кругов Эйлера  а)  B⋃C⋂A ;   б)   C ⋃ A \ B

4.         Найдите   А ⋂ В ⋂ А ⋃ В, если:

1) А = {16; 18;20; 22}           В = {6; 8;0;2}

2) А = {a, в, с, d, k}               В = {в, с, d, m}

3) А = {1,2,3,4,5,6}                В = {2; 4; 6}    

5.        Найдите объединение  множество решений неравенств, в которых переменная – действительное число   -7 ≤ х < 5  и  -5 ≤ х ≤ 8   

6.         Используя круги Эйлера, проиллюстрируйте справедливость переместительного закона пересечения и объединения множеств.  

7.         Запишите распределительный закон пересечения и объединения множеств.

8.     Найдите  А⋃ В \ А ⋂В, если А = {-1; 3} В = [-2; 2].

Самостоятельная (внеаудиторная) работа

изучить определения соответствий; Решение упражнений на композицию соответствий, отображения и их свойства

Раздел 3 Теория графов

Тема 3.1 Введение в теорию графов

Устный опрос

-        Определение соответствий. Обратное соответствие. Композиция соответствий. Отображения и некоторые свойства отображения. Отображения, заданные на одном множестве.

Самостоятельная (внеаудиторная) работа

Опорный конспект по теме: « Определение графа, основные обозначения»

 

Тема 3.2 Различные графы

Устный опрос

-        Содержание учебного материала. Определение графов и основные понятия. История теории графов. Операции над графами. Математические структуры для представления графа.

Самостоятельная (внеаудиторная) работа

Отчет по изученной теме: «различные виды обходов графов и их применение»

Практическое занятие № 3

Решение задач: «Распознавание мостов и разделяющих вершин в графе, нахождение расстояния между вершинами в графе; проверка графа на двудольность; проверка пары графов на изоморфность»

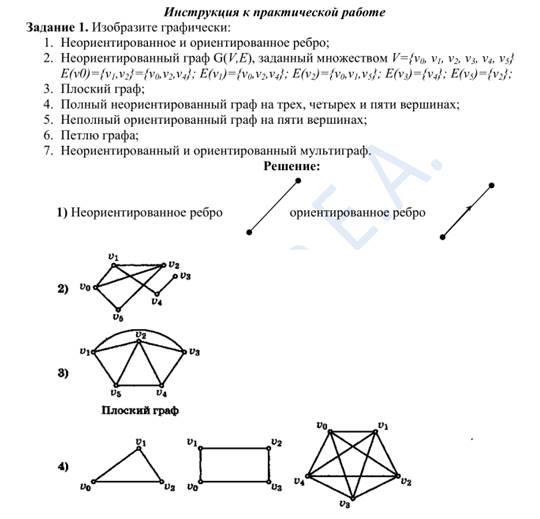
Практическое занятие № 4

Решение задач: «Ориентированные, упорядоченные и бинарные деревья. Обходы бинарных деревьев. Кратчайший остов».

1.    Постройте матрицу смежности и инцидентности для ориентированного графа на рисунке 2.29, стр. 99 учебника [1], согласно вашему варианту. Найти  число степеней входа и выхода данного графа.

2.    Установите на диск D:\Практикум программу Grafoanalizator1.3.3_install.exe (исходный файл находится по адресу студенты на Server\lab223\Заготовки.

3.    Выполните задание по образцу.

Изобразите графически в программе: G(V,Х) - орграф. V={1,2,3,4}, E={(1, 2), (4, 3), (3, 4), (3, 1), (4, 1)}. С помощью программы Grafoanalizator1.3.3, выбрав меню Алгоритмы и особые алгоритмы, ответьте в тетради на вопросы:
  

а)      Является ли граф деревом?

б)      Каково минимальное оставное дерево?

в)      Связный граф?

г)      Планарный граф?

д)      Какие Эйлеровы и Гамильтоновы пути и цепи существуют у графа?

4.      Изобразите графы в Grafoanalizator1.3.3. Полученные графы сохранить в свои папки.

 

а)

б)

в)

 

Тема 3.3. Алгоритмы обхода графов. Транспортные сети

Работа с карточками

Вариант 1 1.       Понятие графа, мост графа, цикл, маршрут, полный граф, связный граф, дополнение к графу  С ПРИМЕРАМИ. 2.       Понятие цикл графа, маршрут, степень вершины, инцидентности ребра 3.       Начертите граф, содержащий 4 висячих и две изолированные вершины. Определите степень вершин,  длину пути  графа , перечислите инцидентные ребра и вершины	Вариант 2 1.       Понятие ориентированного графа, нуль граф, полный граф. Виды графов с примерами. 2.       Понятие маршрут оргграфа, степень вершины, инцидентности ребра 3.       Начертите граф, содержащий шесть висячих и две изолированные вершины. Определите степень вершин и длину пути  графа, перечислите инцидентные ребра и вершины
Вариант 3 1.       Понятие графа, виды графов (полный, нуль, связный, орграф, граф дополнение )с примерами. 2.       Понятие цикл графа, маршрут, степень вершины, инцидентности ребра 3.       Начертите граф, содержащий 4 висячих и две изолированные вершины. Определите степень вершин,  длину пути  графа , перечислите инцидентные ребра и вершины	Вариант 4 1.       Понятие графа, мост, степень вершин и ребер, изоморфный граф.  Виды графов с примерами. 2.       Понятие маршрут оргграфа, степень вершины, инцидентности ребра 3.      Начертите граф, содержащий шесть висячих и две изолированные вершины. Определите степень вершин и длину пути  графа, перечислите инцидентные ребра и вершины

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №5-6, Индивидуальная контрольная работа: «нахождение минимальных маршрутов»

задание: Найти минимальный маршрут по заданию преподавателя.

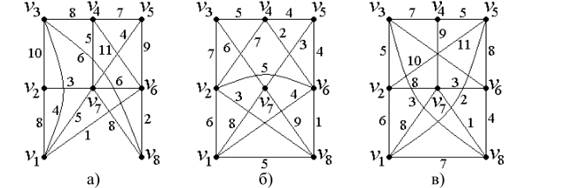
Практическое занятие № 5

Решение задач в программе Delphi по теме «Компоненты связности. Непересекающиеся цепи и  разделяющие множества» Алгоритм Краскала

1.      Задача №1. Найти остов минимального веса с помощью алгоритма Краскала., проверить программой Grafoanalizator1.3.3.

 

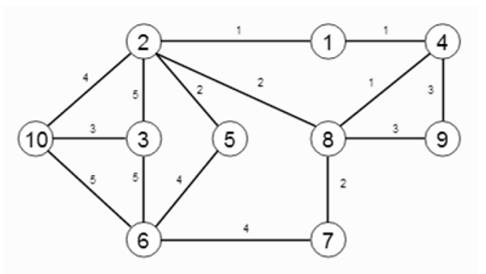
2.      Задача №2 Найти минимальное остовное дерево в неориентированном нагруженном графе. Результат проверить программным обеспечением.

 

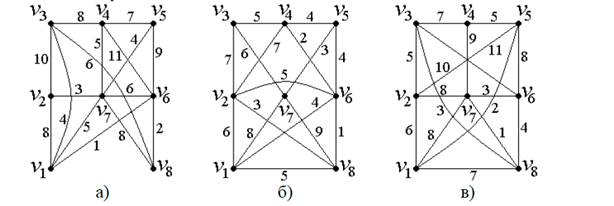
3.      Выполните в тетради упражнение №2.12 (2-5) стр.103 из учебника [1] по вариантам. Вариант  определяет преподаватель.

 

Практическое занятие № 6

Решение задач в программе Delphi по теме «Потоки в сетях»

Раздел 4 Математическая логика

Тема 4.1 Алгебра логики

Устный опрос

-        Алгоритмы обхода графов. Поиск в ширину и глубину.

-        Транспортные сети: основные понятия и определения. Применение алгоритмов на графах в коммуникационных сетях.

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №7

Самостоятельное изучение материалов по темам:

1. Решение задач на представление логических функций в виде совершенной дизъюнктивной и совершенной конъюнктивной нормальной формы»

2. Построение таблицы истинности для формулы логики.

3. Построение таблицы истинности для ДНФ упрощенным методом.

4. Упрощение формул логики с помощью равносильных преобразований.

Практическое занятие № 7

Решение задач на представление логических функций в виде совершенной дизъюнктивной и совершенной конъюнктивной нормальной формы»

1        Выполните  задания упражнения № 4.1 стр.199 учебника для своего варианта. Доказательство эквивалентности выполните, построив таблицы истинности для каждой функции.

2        Постройте  СДНФ и  СКНФ по заданной таблице истинности:

а) x1 x2 x3 F 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1

б) x1 x2 x3 F 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0

x1 x2 x3 F 0 0 0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 в)

 

Тема 4.2 Законы логики Равносильные преобразования

Проверочная работа

«Упрощение логических функций»

1 вариант

 

1. Упростите выражение:

а)

б)

в)

г) (

2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)

2 вариант

 

1. Упростите выражение:

а)

б)

в)

г)

2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)

3 вариант

 

1. Упростите выражение:

а)

б)

в)

г)

2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)

4 вариант

 

 

1. Упростите выражения:

а)

б)

в)

г)

2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №8-9, Решение задач по теме: «Выполнение операций в алгебре вычетов»

Практическое занятие № 8

Решение задач по теме: «Упрощение формул логики с помощью равносильных преобразований»

1. Проверить равносильности двумя способами: построив таблицу истинности и упростив левую и правую части.
2. Упростить логические формулы.

Примечание. Все задания выполняются в соответствии с номером варианта.

Вариант 1

1. ;
2. ;

Вариант 2

1. ;
2. .

Вариант 3

1. 
2. .

Вариант 4

1. .
2. 

Вариант 5

1. ;
2. .

Вариант 6

1.      ;

2.      .

Вариант 7

1.      ;

2.      .

Практическое занятие №9

Решение задач по теме: «Упрощение формул логики с помощью равносильных преобразований»

1. Используя таблицы истинности, докажите следующие эквивалентности:

Таблица 1 – Задание № 1

№ варианта	Исходные данные

2. Упростите высказывания и сравните таблицы истинности условия и ответа. Сделайте вывод об истинности:

Таблица 2 – Задание № 2

№ варианта	Исходные данные

3. Записать формулы в приведенном виде (содержащим только операции    над простыми переменными).

Таблица 3 – Задание № 3

№ варианта	Исходные данные

Требования к отчету: Отчет должен содержать:

- название практической работы;

- формулировку цели работы;

- краткие теоретические сведения по теме работы в виде таблиц, графиков, диаграмм, схем, рисунков и формул;

- результаты решения заданий;

- выводы по работе;

- краткие письменные ответы на контрольные вопросы.

 

Раздел 5 Булевы функции

Тема 5.1 Функции алгебры логики

Устный опрос

-        Равносильные формулы. Законы логики.

-        Методика упрощения формул логики с помощью равносильных преобразований.

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №10-12, Индивидуальное дифференцированное домашнее задание: «представление булевой функции (N≤3) в виде минимальной ДНФ графическим методом»

Практическое занятие № 10

Представление булевой функции в виде совершенной ДНФ

Выполнение работы

1.      По заданной функции постройте таблицу истинности,  СДНФ, приведите функцию к минимальной ДНФ. Постройте соответствующий логический элемент.

а) F(x₁,x₂,x₃) = 

б) F(x₁,x₂,x₃) =

в) F(x₁,x₂,x₃) =

г) F(x₁,x₂,x₃) =

д) F(x₁,x₂,x₃) =

е) F(x₁,x₂,x₃) =

2.      Выполните задание №4.2 стр199 учебника по вариантам.

 

Практическое занятие № 11

Представление булевой функции в виде совершенной КНФ

Задание №1 Определить истинность или ложность высказываний:

1.«2 2=5» и «2 2=4»

2.«2 2=5» или «2 2=4»

3.«2 2=5» и «2 2=4» или «2 2=3»

4.«2 2=5» или «2 2=4» или «2 2=3»

5.«2 2=5» или «2 2=4» и не «2 2=3»

6.«2 2=4» и не «2 2=3» и не «2 2=5»

Задание №2 Построить таблицу истинности:

1.q r p r q ;

2.r p r p .

Таблица 1 - Варианты значения функции

 

 Продолжение таблицы 1

Задание №3 Построить конъюнктивную нормальную форму (КНФ) для функции своего варианта (варианты представлены в таблице15), который определяется по номеру в журнале.

Задание №4 Построить минимальную конъюнктивную (МКНФ) формы функции с использованием методаКарно-Вейчадля функции своего варианта (варианты представлены в таблице), который определяется по номеру в журнале.

Практическое занятие № 12

Представление булевой функции в виде минимальной ДНФ

3.      Минимизируйте булеву функцию с помощью диаграмм Вейча:

а)     

б)     

в)     

4.      Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.

 

 

Вариант 1 а) X1 X2 X3 F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0	X1 X2 X3 F 0 0 0 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 Вариант 2 а)	X1 X2 X3 F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 Вариант 3 а)
б)   X1 X2 X3 F 0 0 0 1 0 0 1 0 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 1	б) X1 X2 X3 F 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0	б) X1 X2 X3 F 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 1

 

Тема 5.2 Операция двоичного сложения. Многочлен Жегалкина

Устный опрос

-        Понятие булева вектора (двоичного вектора). Соседние векторы. Противоположные векторы. Единичный N-мерный куб.

-        Понятие булевой функции (функции алгебры логики). Способы задания булевой функции. Проблема представления булевой функции в виде формулы логики.

-        Понятие совершенной ДНФ. Методика представления булевой функции в виде совершенной ДНФ.Понятие совершенной КНФ. Методика представления булевой функции в виде совершенной КНФ Понятие минимальной ДНФ. Соответствие между гранями единичного N-мерного куба и элементарными произведениями. Методика представления булевой функции (N £ 3) в виде минимальной ДНФ графическим методом.

Самостоятельная (внеаудиторная) работа

Презентация по теме «многочлены И. И. Жегалкина и их применение», составление опорного конспекта по данной теме.

Тема 5.3 Полнота множества функций. Важнейшие замкнутые классы. Теорема Поста

Устный опрос

-        Операция двоичного сложения и ее свойства. Многочлен Жегалкина. Методика представления булевой функции в виде многочлена Жегалкина.

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №13, Реферат по теме «Штрих Шеффера и стрелка Пирса»

Практическое занятие № 13

Проверка булевой функции на принадлежность к классам Т0, Т1, S, L, M; проверка множества булевых функций на полноту.

1. Исследовать на полноту системы булевых функций:

1) {, ∨, 0}

2) {,  , 0}

3) {,  , ↔}

2. К каким функционально замкнутым классам принадлежит булева функция:

1)           f = 11000101

2)           f = 11110100

3)           f = 01001010

6.  Задание:  [1] гл.2 §10-11

 

Тема 5.4 Метод математической индукции

Устный опрос

-        Понятие выражения одних булевых функций через другие. Проблема возможности выражения одних булевых функций через другие. Полнота множества функций. Замыкание множества функций..

-        Понятие замкнутого класса функций. Важнейшие замкнутые классы: Т0 (класс функций, сохраняющих константу 0), Т1 (класс функций, сохраняющих константу 1), S (класс самодвойственных функций), L (класс линейных функций), M (класс монотонных функций).

-        Теорема Поста. Шефферовские функции. Функция Шеффера и функция Пирса как простейшие шефферовские функции.

 

Раздел 6 Предикаты. Бинарные отношения

Тема 6.1 Предикаты

Устный опрос

-        Принцип метода математической индукции. Некоторые разновидности (модификации) метода математической индукции.

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №14-15, Презентации по темам «Предикаты, логические и кванторные операции над ними», «Решение примеров на формализацию предложений с помощью логики предикатов»

Практическое занятие № 14

Решение упражнений по теме: «Определение логического значения для высказываний типов "x P(x), $x P(x), "x $y P(x, y), $x "y P(x, y)»

Задание 1. Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы .

Задание 2. Пусть Р(х) – предикат «х – четное число», определенный на множестве М. Дать словесную формулировку высказыванию , определить его истинность.

Задание 3. Пусть N(х) – предикат «х – натуральное число». Рассмотреть варианты навешивания кванторов. Проинтерпретировать полученные высказывания и определить их истинность.

Задание 4. Записать предикатной формулой предложение «Любой человек имеет отца».

Задание 5. Пусть предикат Р(х, у) описывает отношение «х любит у» на множестве людей. Рассмотреть все варианты навешивания кванторов на обе переменные. Дать словесную интерпретацию полученных высказываний.

а)  ЛЮБИТ (х,у)

   

б)  ЛЮБИТ (х,у)

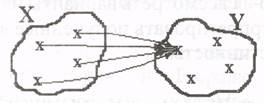
в)  ЛЮБИТ (х,у)

г)  ЛЮБИТ (х,у)

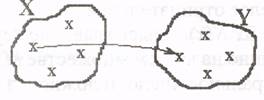
д)  ЛЮБИТ (х,у)

е)  ЛЮБИТ (х,у)

 

Практическое занятие № 15

Решение упражнений по теме «Построение отрицаний к предикатам; формализация предложений с помощью логики предикатов»

Решите следующие задания:

Выразить области истинности предиката через области истинности предикатов  и , если:

1. ;      

2.  ;

3.   ;

          Найти отрицание следующих формул:

1. ;         

2. ;

3. ;                 

4. ;

5. ;

6..

 

6.  Задание:  [1] гл.4 §18-20

 

Тема 6.2 Бинарные отношения

Устный опрос

-         Понятие предиката. Область определения и область истинности предиката. Обычные логические операции над предикатами. Кванторные операции над предикатами. Понятие предикатной формулы; свободные и связанные переменные. Построение отрицаний к предикатам, содержащим кванторные операции. Формализация предложений с помощью логики предикатов. 

Самостоятельная (внеаудиторная) работа

Отчет по изученным темам: 1. Запись области истинности предиката.

2. Определение логического значения для высказываний типов "x P(x), $x P(x), "x $yP(x, y), $x"yP(x, y).

3. Построение отрицаний к предикатам, содержащим кванторные операции.

 

Раздел 7 Элементы теории автоматов

Тема 7.1 Введение в теорию автоматов

Устный опрос

-        Понятие бинарного отношения; примеры бинарных отношений. Диаграмма бинарного отношения. Рефлексивные бинарные отношения.

-        Симметричные бинарные отношения. Транзитивные бинарные отношения. Отношение эквивалентности; теорема о разбиении множества на классы эквивалентности.

Самостоятельная (внеаудиторная) работа

Построение автоматов, распознающих заданные свойства слова.

 

Тема 7.2 Логические конечные автоматы. Схемы алгоритмов и потоков

Устный опрос

-        Базовые множества для автомата: входной алфавит, выходной алфавит, множество состояний. Таблица автомата. Принцип работы автомата. Диаграмма автомата. Словарная функция автомата. Финальная функция автомата. Правильный автомат (автомат Мура). Упрощённый вид диаграммы для правильных автоматов. Автомат, распознающий свойство слова, и его построение.

Самостоятельная (внеаудиторная) работа

отчёт по практическому  занятию №16, Построение схем алгоритмов и потоков данных

 

Практическое занятие № 16

Работа в группе, решение задач: «Разрешимые и неразрешимые проблемы. Схемы алгоритмов. Схемы потоков данных»

Задание

 

4.2Промежуточная аттестация

 

Вопросы к экзамену по дисциплине «ОП.08 Дискретная математика»

для студентов специальности 09.02.01 Компьютерные системы и  комплексы, 2 курс

Вопросы теоретической части:

1. Понятие множеств. Язык теории множеств.
2. Изображение множеств. Подмножества, универсальные множества, мощность множества.
3. Способы задания множеств.
4. Операции над множествами: объединение множеств, пересечение множеств, разность множеств.
5. Универсальные множества. Дополнение множества. Разбиения множества. Диаграммы Эйлера-Венна
6. Кортеж. Прямое произведение множеств.  Декартово произведение множеств
7. Определение соответствий. Обратное соответствие. Композиция соответствий.
8. Определение графов и основные понятия (вершины, ребра, степень вершины, виды вершин).
9. Виды графов (полный, ориентированный, связный, с висячими вершинами, изоморфный, циклический, нуль-граф).
10. Операции над графами
11. Деревья. Лес. Разрезы
12. Эйлеровы и Гамильтоновы графы
13. Транспортные сети: основные понятия и определения.
14. Булевы функции двух переменных, их три категории.
15. Определение значения логических функций.
16. Составление таблиц истинности сложных функций.
17. Формулы алгебры логики, позволяющие производить тождественные преобразования логических выражений.
18. Формы представления логических функций.
19. Построение совершенной нормальной формы логической функции по таблице истинности или ее нормальной форме
20. Упрощение логических функций с помощью законов алгебры логики.
21. Метод минимизации логических функции с помощью карт Карно или диаграмм Вейча.
22. Свойства сложения по модулю два (М2 или строгой дизъюнкции)
23. Понятие предиката. Область определения и область истинности предиката.
24. Операции над предикатами.
25. Понятие предикатной формулы; свободные и связанные переменные.
26. Построение отрицаний к предикатам, содержащим кванторные операции.
27. Формализация предложений с помощью логики предикатов. 
28. Диаграмма бинарного отношения. Рефлексивные бинарные отношения
29. Отношение эквивалентности; теорема о разбиении множества на классы эквивалентности.
30. Базовые множества для автомата: входной алфавит, выходной алфавит, множество состояний
31. Таблица автомата. Принцип работы автомата. Диаграмма автомата.
32.  Словарная функция автомата. Финальная функция автомата.

ПРИМЕРНЫЕ задания  практической части:

1        Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующее множество и изобразите его кругами Эйлера:

2        Выполните действия и определите мощность полученного множества

3        По заданной функции постройте таблицу истинности, приведите функцию к минимальной ДНФ:
 

4        Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y ≡ Z) и F2 = (X → Y) ≡ (X → Z)

5        Используя законы алгебры логики доказать справедливость Закона склеивания относительно дизъюнкции и конъюнкции:    и     .

6        Проверьте, являются ли булевы функции F₁ и F₂  эквивалентными, если  и .

7        Построить таблицу истинности для следующей формулы: A & (B Ú Þ )

8        Упростите функцию, приведя ее к минимальной ДНФ: F(x₁,x₂,x₃) =

9        Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:

X1 X2 X3 F 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1

10    Минимизируйте булеву функцию с помощью карт Карно:

11    Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.

X1	X2	X3		F
0	0	0		1
0	0	1		1
0	1	0		1
0	1	1		0
1	0	0		0
1	0	1		1
1	1	0		1
1	1		1	0

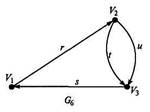
12    Определите по рисунку слева вид графа и постройте таблицы инцидентности и смежности

Преподаватель

___________________  М. В.Алексеева

 

 

 

 

 

 

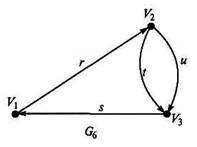
Экзаменационный билет № 1

1. Изображение множеств. Подмножества, универсальные множества, мощность множества
2. Упрощение логических функций с помощью законов алгебры логики
3. Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующее множество и изобразите его кругами Эйлера:

Экзаменационный билет № 2

1. Изображение множеств. Подмножества, универсальные множества, мощность множества
2. Свойства сложения по модулю два (М2 или строгой дизъюнкции)
3. Проверьте, являются ли булевы функции F1 и F2 эквивалентными:

F1 = X → (Y ≡ Z) и F2 = (X → Y) ≡ (X → Z)

Экзаменационный билет № 3

1. Понятие множеств. Язык теории множеств
2. Метод минимизации логических функции с помощью карт Карно или диаграмм Вейча
3. Определите по рисунку справа вид графа, степени его вершин. Имеет ли граф висячие вершины?

 

 

 

 

 

 

Экзаменационный билет № 4

1. Способы задания множеств
2. Определение графов и основные понятия (вершины, ребра, степень вершины, виды вершин).
3. Проверьте, являются ли булевы функции F1 и F2 эквивалентными:

F1 = X ∙ (Y ≡ Z) и F2 = (XY) ≡ (XZ)

Экзаменационный билет № 5

1. Операции над графами
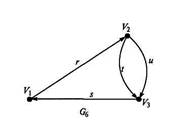2. Составление таблиц истинности сложных функций
3. Определите по рисунку слева вид графа и постройте таблицы инцидентности и смежности

Экзаменационный билет № 6

1. Определение графов и основные понятия (вершины, ребра, степень вершины, виды вершин).
2. Упрощение логических функций с помощью законов алгебры логики
3. Даны отрезки А = [-7; 3], B = [1; 5], C = [4; 10]. Найдите следующие множества и изобразите их кругами Эйлера:

Экзаменационный билет № 7

1. Универсальные множества. Дополнение множества. Разбиения множества. Диаграммы Эйлера-Венна
2. Упрощение логических функций с помощью законов алгебры логики
3. Постройте совершенную ДНФ по таблице истинности:

X1	X2	F
0	0	1
0	1	0
1	0	0
1	1	1

Экзаменационный билет № 8

1.      Логические конечные автоматы с памятью

2.      Операции над графами

3.      Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y Ú Z) и F2 = (X → Y) Ú (X → Z);

Экзаменационный билет № 9

1. Виды графов (полный, ориентированный, связный, с висячими вершинами, изоморфный, циклический, нуль-граф)
2. Упрощение логических функций с помощью законов алгебры логики
3. Выполните действия и определите мощность полученного множества

Экзаменационный билет № 10

1. Построение совершенной нормальной формы логической функции по таблице истинности или ее нормальной форме
2. Виды графов (полный, ориентированный, связный, с висячими вершинами, изоморфный, циклический, нуль-граф)
3. Используя законы алгебры логики доказать справедливость Закона склеивания относительно дизъюнкции и конъюнкции:    и     .

Экзаменационный билет № 11

1.      Структуры данных различного типа. Записи. Работа со структурами.

2.      Простые типы данных в Ассемблере.

3.      Разработка, отладка и выполнение простой программы в Pascal.

Экзаменационный билет № 12

1. Транспортные сети: основные понятия и определения
2. Понятие предиката. Область определения и область истинности предиката

3        Проверьте, являются ли булевы функции F₁ и F₂  эквивалентными, если  и .

Экзаменационный билет № 13

1. Булевы функции двух переменных, их три категории
2. Словарная функция автомата. Финальная функция автомата
3. Проверьте, являются ли булевы функции F₁ и F₂  эквивалентными, если  и

Экзаменационный билет № 14

1. Определение значения логических функций
2. Формализация предложений с помощью логики предикатов

3.      Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ:

X1 X2 X3 F 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1

Экзаменационный билет № 15

1. Булевы функции двух переменных, их три категории
2. Таблица автомата. Принцип работы автомата. Диаграмма автомата
3. Минимизируйте булеву функцию с помощью карт Карно или диаграмм Вейча:

Экзаменационный билет № 16

1. Сравнение логических функций и определение их тождественности
2. Понятие предикатной формулы; свободные и связанные переменные

3.      Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:

X1 X2 X3 F 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0

Экзаменационный билет № 17

1. Виды графов(полный, ориентированный, связный, с висячими вершинами, изоморфный, циклический, нуль-граф).
2. Булевы функции двух переменных, их три категории
3. Докажите или опровергните:

Экзаменационный билет № 18

1. Операции над множествами: объединение множеств, пересечение множеств, разность множеств
2. Виды графов(полный, ориентированный, связный, с висячими вершинами, изоморфный, циклический, нуль-граф).
3. Построить таблицы истинности алгебраически для следующей формулы: A Ú (B Ú Þ)

Экзаменационный билет № 19

1. Транспортные сети: основные понятия и определения
2. Изображение множеств. Подмножества, универсальные множества, мощность множества
3. Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.

Экзаменационный билет № 20

1. Понятие множеств. Язык теории множеств
2. Операции над графами
3. Вычислите значение функции F(x₁, x₂, x₃) при заданных значениях аргументов x₁ = 0, x₂ =0, x₃ = 1 и при x₁ = 0, x₂ = 1, x₃ = 1: F(x₁,x₂,x₃) =

Экзаменационный билет № 21

1.      Полный и неполный условный оператор. Операторные скобки.

2.      Сегменты памяти и сегментные регистры в Assemblere.

3. Разработка, отладка и выполнение программы с использованием линейных алгоритмов.

Экзаменационный билет № 22

1. Виды графов
2. Построение совершенной нормальной формы логической функции по таблице истинности или ее нормальной форме

3.      Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:

Экзаменационный билет № 23

1. Базовые множества для автомата: входной алфавит, выходной алфавит, множество состояний
2. Составление таблиц истинности сложных функций

3.      Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y ≡ Z) и F2 = (X → Y) ≡ (X → Z)

Экзаменационный билет № 24

1. Определите по рисунку слева вид графа и постройте таблицы инцидентности и смежности
2. Операции над множествами: объединение множеств, пересечение множеств, разность множеств.
3. Базовые множества для автомата: входной алфавит, выходной алфавит, множество состояний

 

 

 

 

Экзаменационный билет № 25

1. Составление таблиц истинности сложных функций.
2. Упрощение логических функций с помощью законов алгебры логики.
3. Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.

Экзаменационный билет № 26

1. Универсальные множества. Дополнение множества. Разбиения множества. Диаграммы Эйлера-Венна
2. Таблица автомата. Принцип работы автомата. Диаграмма автомата
3. Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующее множество и изобразите его кругами Эйлера:

Экзаменационный билет № 27

1. Понятие предиката. Область определения и область истинности предиката
2. Определение графов и основные понятия (вершины, ребра, степень вершины, виды вершин).
3. Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.

 

5. Критерии оценки индивидуальных образовательных достижений по результатам текущего и  промежуточного  контроля

 

5.1.Оценка индивидуальных образовательных достижений обучающихся по результатам текущего контроля и промежуточной аттестации производится в соответствии с системой  оценки устного опроса, решения задач, контрольных работ, письменных работ, тестирования, заполнения таблиц, диктантов, ответов на вопросы билетов промежуточной аттестации, выполнения заданий билетов промежуточной аттестации и т.д.:

без ошибок – отлично;

не более 2х неточностей/ошибок – хорошо;

3-4 ошибки – удовлетворительно;

более 4х ошибок, нераскрытие темы, невыполнение задания - неудовлетворительно.

 

 

6. Рекомендуемая литература для разработки оценочных средств и подготовке обучающихся к аттестации

1.      Баврин  И. И. Дискретная математика. Учебник и задачник : для СПО / И. И. Баврин. — М. : Издательство Юрайт, 2017. — 209 с. — (Серия : Профессиональное образование). — ISBN 978-5-534-01595-9.https://www.biblio-online.ru/book/46422B2A-1497-4FFD-8A53-143190428418

2.      Дискретная математик: учебник и практикум для академического бакалавра/С.Б.Гашков, А.Б.Фролов- 2-е.изд.испр. и доп.-М.:Издательство Юрайт, 2017.-448-(Серия:Бакалавр. Академический выпуск).  https://www.biblio-online.ru/book/D7F91C17-137D-4B22-8B74-EA7E8114E31E.

Дополнительная:

3.     Соболева Т.С., Чечкин А.В. Дискретная математика: Учебник для студ. высшего. проф. образования –М.: Издательский центр «Академия», 2015. – 256 с.

Информационные ресурсы

4.     http://rain.ifmo.ru/cat/view.php - Дискретная математика:алгоритмы

5.     https://testserver.pro/run/test/4303/4872 - тест по дискретной математике

http://math.nsc.ru/LBRT/k3/- Лаборатория дискретного анализа

Авторы-составители:

преподаватели

Алексеева М.В.

 

Скачано с www.znanio.ru