
2 КЛАССИФИКАЦИЯ МЕТОДОВ ОПТИМИЗАЦИИ
Методы оптимизации классифицируют в соответствии с задачами оптимизации:
Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции этот экстремум единственен и будет глобальным максимумом/минимумом.
Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.
Существующие в настоящее время методы поиска можно разбить на три большие группы:
1) детерминированные;
2) случайные (стохастические);
3) комбинированные.
По критерию размерности допустимого множества методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
По виду целевой функции и допустимого множества задачи оптимизации и методы их решения можно разделить на следующие классы:
Задачи оптимизации, в которых целевая функция ![]() и
ограничения
и
ограничения ![]() являются линейными функциями,
разрешаются так называемыми методами линейного программирования.
являются линейными функциями,
разрешаются так называемыми методами линейного программирования.
В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
если ![]() и
и ![]() –
выпуклые функции, то такую задачу называют задачей выпуклого
программирования;
–
выпуклые функции, то такую задачу называют задачей выпуклого
программирования;
если ![]() , то имеют дело с задачей целочисленного
(дискретного) программирования.
, то имеют дело с задачей целочисленного
(дискретного) программирования.
По требованиям к гладкости и наличию у целевой функции частных производных их также можно разделить на:
прямые методы, требующие только вычислений целевой функции в точках приближений;
методы первого порядка: требуют вычисления первых частных производных функции;
методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.
Помимо того, оптимизационные методы делятся на следующие группы:
аналитические методы (например, метод множителей Лагранжа и условия Каруша – Куна – Таккера);
численные методы;
графические методы.
В зависимости от природы множества X задачи математического программирования классифицируются как:
задачи дискретного программирования (или комбинаторной оптимизации) – если X конечно;
задачи целочисленного программирования – если X является подмножеством множества целых чисел;
задачи нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
Если же все ограничения и целевая функция содержат лишь линейные функции, то это – задача линейного программирования.
Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.
3 МЕТОДЫ ПОИСКА МИНИМУМА ОДНОМЕРНЫХ УНИМОДАЛЬНЫХ ФУНКЦИЙ
Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:
f(x) → min ,
x принадлежит [a;b].
Максимизация целевой функции эквивалента минимизации f(x) → max эквивалентна минимизации противоположной величины (–f(x) → min), поэтому можно рассматривать только задачи минимизации.
К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того, необходимость в минимизации функций одной переменной возникает при реализации некоторых методов решения более сложных задач оптимизации.
Для решения задачи минимизации функции f(x) на отрезке [a;b] на практике, как правило, применяют приближенные методы. Они позволяют найти решения этой задачи с необходимой точностью в результате определения конечного числа значений функции f(x) и ее производных в некоторых точках отрезка [a;b]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.
Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, – это возможность определения значений f(x) в заданных точках.
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке [a;b].
Функция f(x) называется унимодальной на отрезке [a;b], если она непрерывна на [a;b] и существуют числа α и β, a ≤ α ≤ β ≤ b, такие, что:
1) если a < α,
то f(x) монотонно убывает при ![]()
2) если ![]() , то f(x)=
f* =
, то f(x)=
f* =![]()
3) если β < b, то f(x)
монотонно возрастает при ![]()
Множество унимодальных на отрезке [a;b] функций будем обозначать через Q[a;b].
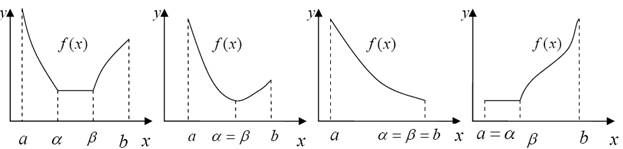 Отметим, что возможно вырождение в
точку одного или двух отрезков из [a;α],
[α;β] и [β;b].
Некоторые варианты расположения и вырождения в точку отрезков монотонности и
постоянства унимодальной функции показаны на рисунке 3.1.
Отметим, что возможно вырождение в
точку одного или двух отрезков из [a;α],
[α;β] и [β;b].
Некоторые варианты расположения и вырождения в точку отрезков монотонности и
постоянства унимодальной функции показаны на рисунке 3.1.
Рис. 3.1. Графики унимодальных функций
Основные свойства унимодальных функций:
1 Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимума на отрезке [a;b].
2 Функция унимодальная на отрезке [a;b] является
унимодальной на любом меньшем отрезке ![]() .
.
3 Пусть f(x)
![]() Q[a;b] и а ≤ х1
< х2 ≤ b.
Тогда
Q[a;b] и а ≤ х1
< х2 ≤ b.
Тогда
если f(x1)
≤ f(x2),
то х*![]() [a; x2];
[a; x2];
если f(x1)
> f(x2),
то х*![]() [ x1;b],
[ x1;b],
где х* – одна из точек минимума f(x) на отрезке [a;b].
Рассмотрение функций как унимодальных во всей области определения в общем случае невозможно. Однако включение в процесс минимизации предварительного этапа, на котором отрезок минимизации разделяют на несколько отрезков, на каждом из которых минимизируемая функция унимодальна, позволяет избежать ошибок, связанных с нахождением локальных минимумов.
При решении практических задач оптимизации классический метод имеет
ограниченное применение. Это объясняется тем, что, во-первых, во многих случаях
значения целевой функции f(x) находятся из измерений или
экспериментов, а измерение производной ![]() затруднительно
или невозможно и, во-вторых, даже когда производная
затруднительно
или невозможно и, во-вторых, даже когда производная ![]() задана
аналитически или поддается измерению, решение уравнения
задана
аналитически или поддается измерению, решение уравнения ![]() =
0 зачастую вызывает затруднения.
=
0 зачастую вызывает затруднения.
3.1 Метод перебора
Метод перебора или равномерного поиска является простейшим из прямых методов минимизации и состоит в следующем.
Разобьем отрезок [a;b] на n равных частей точками деления:
![]() , i = 0,...n.
, i = 0,...n.
Вычислив значения f(x) в точках xi, путем сравнения найдем точку xm, где m – это число от 0 до n, такую, что
f(xm) = min f(xi) для всех i от 0 до n. (3.1)
Далее положим x* ≈ xm, f* ≈ f(xm).
Замечание:
1 Погрешность определения точки минимума x* функции f(x) методом перебора не превосходит величины ![]() .
.
Предположим, что xm из (3.1) является внутренней точкой разбиения отрезка [a;b], т.е. 1 ≤ m ≤ n – 1 (случаи m = 0 и m = n рассматриваются аналогично). Тогда из соотношения (2.1) с учетом свойства унимодальных функций следует, что:
а) f(xm-1)
≥ f(xm),
т.е. х*![]() [xm-1;b];
[xm-1;b];
б) f(xm)
≤ f(xm+1),
т.е. х*![]() [а;xm+1].
[а;xm+1].
Отсюда получаем, что х*![]() [xm-1;b]
[xm-1;b] ![]() [а;xm+1] = [xm-1;xm+1]. Длина последнего
отрезка равна
[а;xm+1] = [xm-1;xm+1]. Длина последнего
отрезка равна ![]() .
.
Таким образом, чтобы обеспечить требуемую точность ε
определения точки х*, число отрезков разбиения n необходимо выбрать из условия ![]() ≤ ε, т.е. n ≥
≤ ε, т.е. n ≥ ![]() .
.
2 Пусть реализация метода перебора потребовала N вычислений функции f(x). Это означает, что отрезок [a;b] был
разбит на n = N –
1 частей и достигнутая точность определения х* составила ![]() .
.
Поэтому точность решения ε(N), которую обеспечивает метод перебора в результате N вычислений f(x), будет
![]() .
.
Пример. Решить задачу f(x) = x4 + e-x→min, x![]() [0;1] с точностью до ε
= 0,1.
[0;1] с точностью до ε
= 0,1.
Функция f(x) унимодальная на
отрезке [0;1]. Найдем число n отрезков разбиения
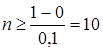 , т.е. можно взять n = 10. Вычислим значения f(x), где xi = 0,1 · i, i =
0,…,10 и запишем их в таблицу 1.
, т.е. можно взять n = 10. Вычислим значения f(x), где xi = 0,1 · i, i =
0,…,10 и запишем их в таблицу 1.
Таблица 1
|
xi |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
f(xi) |
1,00 |
0,90 |
0,82 |
0,75 |
0,70 |
0,67 |
0,68 |
0,74 |
0,86 |
1,06 |
1,37 |
Из таблицы видно, что x* = 0,5, f* = 0,67.
3.2 Метод поразрядного поиска
Рассмотрим возможности усовершенствования метода перебора с целью уменьшения количества значений f(x), которые необходимо находить в процессе минимизации.
Во-первых, если оказывается, что f(xi) ≤ f(xi+1), то отпадает необходимость вычислять f(x) в точках xi+2, xi+3 и т.д., так как х* ≤ xi+1 (см. п. 3.1).
Во-вторых, разумно было бы сначала определить отрезок, содержащий оптимальную точку x*, грубо, т.е. найти точку x* с небольшой точностью, а затем искать ее на этом отрезке с меньшим шагом дискретизации, повышая точность.
Эти возможности улучшения реализованы в методе поразрядного поиска. В этом методе перебор точек отрезка происходит сначала с шагом Δ = xi+1 – xi >ε до тех пор, пока не выполнится условие f(xi) < f(xi+1) или пока очередная из точек не совпадет с концом отрезка. После этого шаг уменьшается (обычно в 4 раза) и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения f(x) снова не перестанут уменьшаться или очередная точка не совпадет с другим концом отрезка и т.д. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг дискретизации не превосходит ε.
Алгоритм метода поразрядного поиска
Шаг 1. Выбрать
начальный шаг ![]() . Положить x0 =
a. Вычислить f(x0).
. Положить x0 =
a. Вычислить f(x0).
Шаг 2. Положить x1 = x0 + Δ. Вычислить f(x1).
Шаг 3. Сравнить f(x0) и f(x1). Если f(x0) > f(x1), то перейти к шагу 4, иначе к шагу 5.
Шаг 4. Положить x0 = x1 и f(x0) = f(x1). Проверить условие принадлежности x0 интервалу (a, b). Если a < x0 < b, то перейти к шагу 2, иначе к шагу 5.
Шаг 5. Проверка на окончание поиска: если |Δ| ≤ ε, то вычисления завершить, полагая x*= x0, f* = f(x0), иначе перейти к шагу 6.
Шаг 6. Изменить направление поиска:
положить x0 = x1, f(x0) = f(x1),
![]() . Перейти к шагу 2.
. Перейти к шагу 2.
Пример.
Решить задачу f(x)=x4+e-x→min, x![]() [0;1]
с точностью до ε = 0,1.
[0;1]
с точностью до ε = 0,1.
Начальный шаг Δ = ¼ = 0,25. Вычисляя последовательно значения f(x) в точках дискретизации с шагом 0,25, получим:
|
х |
0→0,25→0,50→0,75 |
|
f(x) |
1,000 > 0,783 > 0,669 > 0,789 |
Так как f(0,50) < f(0,75), причем |Δ| > ε, то поиск x* продолжаем из начальной точки x0 =0,75, изменив его направление и уменьшив шаг в 4 раза:
|
х |
0,4375←0,5000←0,5625←0,6250←0,6875←0,7500 |
|
f(x) |
0,682 < 0,669 < 0,670 < 0,688 < 0,726 < 0,789 |
Так как |Δ| = 0,0625 < ε, то поиск завершен и x* ≈ 0,5, f* ≈ 0,67.
3.3 Методы исключения отрезков
В методе перебора, рассмотренном выше все точки xi, в которых определяются значения f(x), выбираются заранее. Если же для выбора очередной точки вычисления f(x) использовать информацию, содержащуюся в уже найденных значениях f(x), то поиск точки минимума можно сделать более эффективным, т.е. сократить число определяемых для этого значений f(x), как, например, в методе поразрядного поиска.
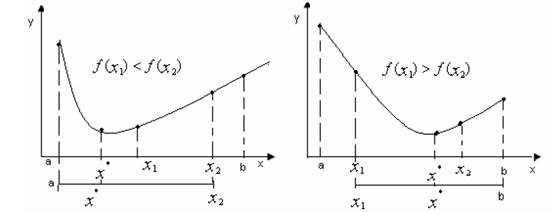 Один из путей такого
более эффективного поиска точки x* указывает свойство 3
унимодальных функций.
Один из путей такого
более эффективного поиска точки x* указывает свойство 3
унимодальных функций.
Рис. 3.2 Уменьшение отрезка поиска точки минимума методами исключения отрезков
Пусть ![]() . Сравнив значения f(x)
в пробных точках x1 и x2, можно сократить
отрезок поиска точки x*, перейдя к отрезку [a;x1],
если f(x1) ≤ f(x2),
или к отрезку [x1;b], если f(x1)
> f(x2) (рис. 3.2). Описанную процедуру можно
повторить необходимое число раз, последовательно уменьшая отрезок, содержащий
точку минимума.
. Сравнив значения f(x)
в пробных точках x1 и x2, можно сократить
отрезок поиска точки x*, перейдя к отрезку [a;x1],
если f(x1) ≤ f(x2),
или к отрезку [x1;b], если f(x1)
> f(x2) (рис. 3.2). Описанную процедуру можно
повторить необходимое число раз, последовательно уменьшая отрезок, содержащий
точку минимума.
Когда длина последнего из найденных отрезков станет достаточно малой,
следует положить х* ≈ ![]() ,
где
,
где ![]() – одна из точек этого отрезка,
например его середина. Методы минимизации, основанные на этом принципе,
называются методами исключения отрезков.
– одна из точек этого отрезка,
например его середина. Методы минимизации, основанные на этом принципе,
называются методами исключения отрезков.
Чтобы относительное уменьшение отрезка на каждой итерации не зависело от того, какая из его частей исключается из дальнейшего рассмотрения, пробные точки следует располагать симметрично относительно середины исходного отрезка. В зависимости от способа выбора пробных точек получаются различные методы исключения отрезков. На практике используются следующие:
Первый метод деления пополам (дихотомии). В этом методе точки х1 и х2 располагаются близко к середине отрезка [a;b], т.е.
![]() , (3.2)
, (3.2)
где ![]() > 0 – малое число. При этом
отношение длин нового и исходного отрезков
> 0 – малое число. При этом
отношение длин нового и исходного отрезков ![]() близко
к
близко
к ![]() , этим и объясняется название
метода.
, этим и объясняется название
метода.
Отметим,
что для любых точек х1 и х2 величина ![]() >
>![]() ,
поэтому указанный выбор пробных точек объясняется стремлением обеспечить
максимально возможное относительное уменьшение отрезка на каждой итерации
поиска х*.
,
поэтому указанный выбор пробных точек объясняется стремлением обеспечить
максимально возможное относительное уменьшение отрезка на каждой итерации
поиска х*.
В
конце вычислений по методу дихотомии в качестве приближенного значения х*
берут середину последнего из найденных отрезков [a;b], убедившись
предварительно, что достигнуто неравенство ![]() .
.
Алгоритм дихотомического поиска
Шаг 1. Определить х1 и х2 по формулам (3.2). Вычислить f(x1) и f(x2).
Шаг 2. Сравнить f(x1) и f(x2). Если f(x1) ≤ f(x2), то перейти к отрезку [a; x2], положив b = x2, иначе – к отрезку [x1;b], положив а = x1.
Шаг 3. Найти
достигнутую точность ![]() . Если εn > ε, то
перейти к следующей итерации, вернувшись к шагу 1. Если εn ≤ ε, то
завершить поиск х*, перейдя к шагу 4.
. Если εn > ε, то
перейти к следующей итерации, вернувшись к шагу 1. Если εn ≤ ε, то
завершить поиск х*, перейдя к шагу 4.
Шаг 4. Положить ![]()
Замечание:
1 Число ![]() из (3.2) выбирается на
интервале (0;2
из (3.2) выбирается на
интервале (0;2![]() ) с учетом следующих
соображений:
) с учетом следующих
соображений:
а) чем меньше ![]() , тем больше
относительное уменьшение длины отрезка на каждой итерации, т.е. при уменьшении
, тем больше
относительное уменьшение длины отрезка на каждой итерации, т.е. при уменьшении ![]() достигается более высокая скорость
сходимости метода дихотомии;
достигается более высокая скорость
сходимости метода дихотомии;
б) при чрезмерно малом ![]() сравнение
значений f(x) в точках х1 и х2,
отличающихся на величину
сравнение
значений f(x) в точках х1 и х2,
отличающихся на величину ![]() , становится
затруднительным. Поэтому выбор
, становится
затруднительным. Поэтому выбор ![]() должен быть
согласован с точностью определения f(x) и с количеством верных
десятичных знаков при задании аргумента х.
должен быть
согласован с точностью определения f(x) и с количеством верных
десятичных знаков при задании аргумента х.
2 Число n итераций метода дихотомии, необходимое для определения точки х* с точностью ε, определяется неравенством
![]() (3.3)
(3.3)
Обозначим длину исходного отрезка [a;b] через ![]() . Длина отрезка, полученного после
первой итерации, будет
. Длина отрезка, полученного после
первой итерации, будет ![]() после второй
итерации
после второй
итерации ![]() после третьей итерации
после третьей итерации ![]() и т.д.
и т.д.
При этом будет
достигнута точность определения точки минимума ![]() .
Находим n из условия
.
Находим n из условия
![]() (3.4)
(3.4)
Величина
![]() может быть выбрана достаточно
малой, поэтому, пренебрегая ею в (3.4), получаем
может быть выбрана достаточно
малой, поэтому, пренебрегая ею в (3.4), получаем ![]() На
каждой итерации метода дихотомии вычисляются два значения f(x).
Поэтому после n вычислений f(x)
производится
На
каждой итерации метода дихотомии вычисляются два значения f(x).
Поэтому после n вычислений f(x)
производится ![]() итераций и достигается
точность определения х*
итераций и достигается
точность определения х*
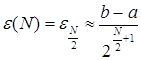 (3.5)
(3.5)
Пример.
Решить задачу f(x)
= x4+e-x→min, x![]() [0;1]
с точностью до ε = 0.1.
[0;1]
с точностью до ε = 0.1.
 Выберем
Выберем ![]() =
0,02.
=
0,02.
Результаты вычисления на остальных итерациях записаны в таблице 2.
Таблица 2
|
Номер итерации |
a |
b |
|
x1 |
x2 |
f(x1) |
f(x2) |
Сравнение f(x1) и f(x2) |
|
2 |
0,49 |
1 |
0,26 |
0,735 |
0,755 |
0,771 |
0,792 |
f(x1) > f(x2) |
|
3 |
0,49 |
0,755 |
0,13 |
0,613 |
0,633 |
0,683 |
0,691 |
f(x1) > f(x2) |
|
4 |
0,49 |
0,633 |
0,07 |
0,07 < 0,1 – точность достигнута |
||||
Таким образом ![]()
![]()
Метод «золотого сечения». Рассмотрим такое симметричное расположение точек х1 и х2 на отрезке [a;b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения f(x), так как другое значение уже найдено из одной из предыдущих итераций.
Найдем точки х1 и х2, обладающие указанным свойством.
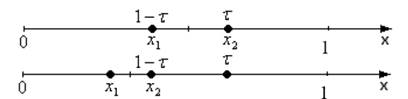 Рассмотрим сначала
отрезок [0;1] и для определенности предположим, что при его уменьшении
исключается правая часть этого отрезка. Пусть
Рассмотрим сначала
отрезок [0;1] и для определенности предположим, что при его уменьшении
исключается правая часть этого отрезка. Пусть ![]() ,
тогда симметрично расположенная точка
,
тогда симметрично расположенная точка ![]() (рис.
3.3).
(рис.
3.3).
Рис. 3.3 К определению пробных точек в методе «золотого сечения»
Пробная
точка х1 на отрезке [0;1] перейдет в пробную точку ![]() нового отрезка [0;
нового отрезка [0;![]() ]. Чтобы точки
]. Чтобы точки ![]() и
и ![]() делили
отрезки в одном и том же соотношении, должно выполняться равенство
делили
отрезки в одном и том же соотношении, должно выполняться равенство ![]() или
или ![]() ,
откуда находим положительное значение
,
откуда находим положительное значение ![]() Таким
образом,
Таким
образом, ![]()
Для произвольного отрезка выражения для пробных точек примут вид:
![]() (3.6)
(3.6)
Замечания:
1 Точки х1 и х2 из (3.6) обладают следующим свойством: каждая из них делит отрезок [a;b] на две части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей частей отрезка. Точки с таким свойством называются точками «золотого сечения» отрезка [a;b]. Это свойство объясняет название рассматриваемого метода.
2 На каждой итерации исключения отрезков с пробными точками (3.6) одна из
них ![]() переходит на следующий отрезок и
значение f(x) в этой точке вычислять не следует. Если новым
отрезком становится [a;х2], то на него переходит
пробная точка х = х1 исходного отрезка, становясь его
второй пробной точкой
переходит на следующий отрезок и
значение f(x) в этой точке вычислять не следует. Если новым
отрезком становится [a;х2], то на него переходит
пробная точка х = х1 исходного отрезка, становясь его
второй пробной точкой ![]() (рис. 3.3). В случае
перехода к отрезку [х1;b] пробная точка
(рис. 3.3). В случае
перехода к отрезку [х1;b] пробная точка ![]() = х2 исходного
отрезка становится первой пробной точкой отрезка [х1;b].
= х2 исходного
отрезка становится первой пробной точкой отрезка [х1;b].
3 Легко проверить, что x1 = a + b – x2 и x2 = a + b – x1. Поэтому на каждой итерации метода «золотого сечения» недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке с помощью сложения и вычитания, не используя формул (3.6).
4 В конце вычислений по методу «золотого сечения» в качестве
приближенного значения х* можно взять середину последнего из
последних полученных отрезков ![]()
На каждой итерации отрезок поиска точки минимума уменьшается в одном и
том же отношении ![]() , поэтому в результате n итераций его длина становится
, поэтому в результате n итераций его длина становится ![]() . Таким образом, точность
. Таким образом, точность ![]() определения точки х*
после n итераций находится из равенства
определения точки х*
после n итераций находится из равенства
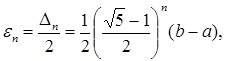 (3.7)
(3.7)
а условием
окончания поиска точки х* с точностью ![]() служит
неравенство
служит
неравенство ![]()
Алгоритм метода «золотого сечения»
Шаг 1. Найти х1 и х2 по формулам
(3.6). Вычислить f(x1) и f(x2).
Положить ![]() ,
, ![]()
Шаг 2. Проверка на окончание поиска: если ![]() ,
то перейти к шагу 3, иначе к шагу 4.
,
то перейти к шагу 3, иначе к шагу 4.
Шаг
3. Переход к новому отрезку и новым пробным точкам. Если f(x1)
≤ f(x2), то положить b
= x2, x2
= x1, f(x1)
= f(x2), ![]() и вычислить f(x1),
иначе положить a = x1,
x1 = x2,
f(x1) = f(x2),
и вычислить f(x1),
иначе положить a = x1,
x1 = x2,
f(x1) = f(x2), ![]() и вычислить f(x2).
Положить
и вычислить f(x2).
Положить ![]() и перейти к шагу 2.
и перейти к шагу 2.
Шаг 4. Окончание поиска: положить ![]() .
.
Пример.
Решить задачу f(x) = x4 + e-x→min, x![]() [0;1]
с точностью до ε = 0,1.
[0;1]
с точностью до ε = 0,1.
Шаг 1. Находим:
x1 = 0,382, x2 = 0,618, f(x1) = 0,704, f(x2) = 0,685, εn = 0,5.
Шаг 2. εn = 0,5 > ε = 0,1, поэтому переходим к шагу 3.
Шаг 3. f(x1) > f(x2), поэтому полагаем a = 0,382, x1 = 0,618, f(x1) = 0,685, x2 = 0,784, εn = 0,309 и вычисляем f(x2) = 0,807. Переходим к следующей итерации, начиная с шага 2.
Результаты вычислений на остальных итерациях представлены в таблице 3.
Таблица 3
|
Номер итерации |
a |
b |
εn |
x1 |
x2 |
f(x1) |
f(x2) |
Сравнение f(x1) и f(x2) |
|
2 |
0,382 |
1,000 |
0,309 |
0,764 |
0,764 |
0,685 |
0,807 |
f(x1) < f(x2) |
|
3 |
0,382 |
0,764 |
0,191 |
0,528 |
0,618 |
0,668 |
0,685 |
f(x1) < f(x2) |
|
4 |
0,382 |
0,618 |
0,118 |
0,472 |
0,528 |
0,673 |
0,668 |
f(x1) < f(x2) |
|
5 |
0,472 |
0,618 |
0,073 |
0,073 < 0,1 – точность достигнута |
||||
Таким образом, ![]() .
.
Замечание. Число
итераций, необходимое для достижения заданной точности ![]() ,
можно найти из условия
,
можно найти из условия ![]() с учетом соотношения
(3.7)
с учетом соотношения
(3.7) 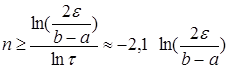 .
.
Так как N вычислений f(x) позволяют выполнить N – 1 итераций метода «золотого сечения», то достигнутая в результате этих вычислений точность определения х* составляет
![]() . (3.8)
. (3.8)
Второй метод деления отрезка пополам. Этот метод, использующий на каждой итерации три пробные точки, обеспечивает последовательное уменьшение длины отрезка, содержащего х*, ровно вдвое.
Рассмотрим способ исключения отрезков, применяемый в рассматриваемом методе.
Разделим
отрезок [a;b] на четыре равные части пробными точками ![]() i =
1, 2, 3. Сравним значения f(x1) и f(x2).
Если f(x1) ≤ f(x2), то
уменьшенный вдвое отрезок поиска точки х* найден – это [a;х2].
Если же f(x1) > f(x2),
то произведем еще одно сравнение значений f(x) при f(x2)
≤ f(x3) перейдем к отрезку [х2;b].
i =
1, 2, 3. Сравним значения f(x1) и f(x2).
Если f(x1) ≤ f(x2), то
уменьшенный вдвое отрезок поиска точки х* найден – это [a;х2].
Если же f(x1) > f(x2),
то произведем еще одно сравнение значений f(x) при f(x2)
≤ f(x3) перейдем к отрезку [х2;b].
Отметим, что каким бы ни оказался новый отрезок, одна из уже использованных пробных точек переходит на его середину, становясь новой точкой х2. Таким образом, для проведения следующей итерации на вновь полученном отрезке потребуется вычисление не более двух новых значений f(x) (либо в точке х1, либо в точке х3).
Алгоритм второго метода деления отрезка пополам
Шаг 1. ![]() . Вычислить значение f(x2),
перейти к шагу 2.
. Вычислить значение f(x2),
перейти к шагу 2.
Шаг 2. Положить ![]() . Вычислить значение f(x1)
и перейти к шагу 3.
. Вычислить значение f(x1)
и перейти к шагу 3.
Шаг 3. Сравнить f(x1) и f(x2).
Если f(x1) ≤ f(x2), то
продолжить поиск на отрезке [a;х2], положив b = x2, x2 = x1,
f(x1) = f(x2), и перейти к
шагу 5, иначе положить ![]() , вычислить
значение f(x3) перейти к шагу 4.
, вычислить
значение f(x3) перейти к шагу 4.
Шаг 4. Сравнить f(x2) и f(x3). Если f(x2) ≤ f(x3), то перейти к отрезку [х1;х3], положив a = x1, b = x3, иначе продолжить поиск на отрезке [х2;b], положив a = x2, x2 = x3, f(x2) = f(x3). Перейти к шагу 5.
Шаг 5. Проверка на окончание поиска. Вычислить ![]() и сравнить с ε. Если
и сравнить с ε. Если ![]() > ε то перейти к
следующей итерации, вернувшись к шагу 2, иначе завершить поиск, положив
> ε то перейти к
следующей итерации, вернувшись к шагу 2, иначе завершить поиск, положив ![]()
Пример.
Решить задачу f(x)=x4+e-x→min, x![]() [0;1]
с точностью до ε = 0.1.
[0;1]
с точностью до ε = 0.1.
Итерация 1
Шаг 1. Находим ![]() , f(x2)
= 0,669. Переходим к шагу 2.
, f(x2)
= 0,669. Переходим к шагу 2.
Шаг 2. Определяем ![]() , f(x1)
= 0,783. Переходим к шагу 3.
, f(x1)
= 0,783. Переходим к шагу 3.
Шаг 3. f(x1) > f(x2),
поэтому полагаем ![]() , вычисляем f(x3)
= 0,789 и переходим к шагу 4.
, вычисляем f(x3)
= 0,789 и переходим к шагу 4.
Шаг 4. f(x2) > f(x3), поэтому a=0,25, b=0,75 и переходим к шагу 5.
Шаг 5. Находим![]() т.е. переходим к
следующей итерации, начиная с шага 2.
т.е. переходим к
следующей итерации, начиная с шага 2.
Результаты вычислений представлены в таблице 4.
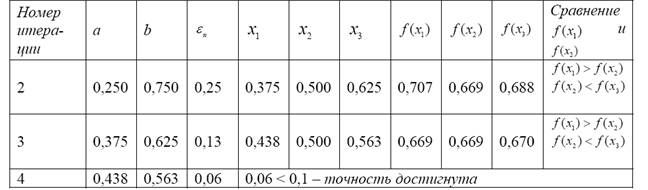 Таблица 4
Таблица 4
Таким образом, ![]()
3.4 Метод парабол
Поиск точки минимума методами исключения отрезков основан на сравнении значений функции в двух точках. При таком сравнении разности значений f(x) в этих точках не учитываются, важны только их знаки.
Учесть информацию, содержащуюся в относительных изменениях значений f(x) в пробных точках, позволяют методы полиномиальной аппроксимации, основная идея которых состоит в том, что для функции f(x) строится аппроксимирующий многочлен, и его точка минимума служит приближением к х*. Для эффективного использования этих методов на функцию f(x), кроме унимодальности, налагается дополнительное требование достаточной гладкости (по крайней мере непрерывности).
Обоснованием указанных методов является известная из математического анализа теорема Вейерштрасса об аппроксимации, согласно которой непрерывную на отрезке функцию можно с любой точностью приблизить на этом отрезке некоторым полиномом.
Для повышения точности аппроксимации можно, во-первых, увеличивать порядок полинома и, во-вторых, уменьшать длину отрезка аппроксимации. Первый путь приводит к быстрому усложнению вычислительных процедур, поэтому на практике используют аппроксимирующие полиномы не выше третьего порядка. В то же время уменьшение отрезка, содержащего точку минимума унимодальной функции, не представляет особого труда.
В простейшем методе полиномиальной аппроксимации – методе парабол – используются полиномы второго порядка. На каждой итерации этого метода строится квадратный трехчлен, график которого (парабола) проходит через три выбранные точки графика функции f(x) (рис. 3.4)
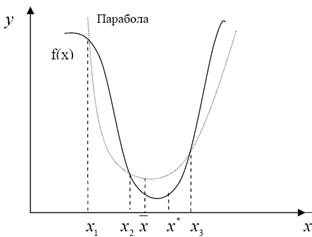 |
Рис. 3.4. Иллюстрация к методу парабол
Опишем метод парабол. Рассмотрим унимодальную функцию f(x) на отрезке [a;b], достигающую минимума во внутренней точке этого отрезка. Выберем три точки x1, x2 и x3 отрезка [a;b], для которых выполняются неравенства
x1 < x2 < x3, f(x1) ≥ f(x2) ≤ f(x3). (3.9)
Из унимодальности f(x) следует, что ![]() .
.
Построим квадратный трехчлен ![]() , график
которого проходит через точки (x1, f(x1)),
(x2, f(x2)), (x3, f(x3))
графика функции f(x). Будем считать, что хотя бы одно из
неравенств (3.9) для f(x1) является строгим (если f(x1)
= f(x2) = f(x3), то
поиск точки
, график
которого проходит через точки (x1, f(x1)),
(x2, f(x2)), (x3, f(x3))
графика функции f(x). Будем считать, что хотя бы одно из
неравенств (3.9) для f(x1) является строгим (если f(x1)
= f(x2) = f(x3), то
поиск точки ![]() на этом закончен, так как из
унимодальности функции f(x) следует, что она достигает минимума в
каждой точке отрезка
на этом закончен, так как из
унимодальности функции f(x) следует, что она достигает минимума в
каждой точке отрезка ![]() ). Тогда из (3.9)
следует, что ветви параболы направлены вверх, а точка минимума трехчлена
). Тогда из (3.9)
следует, что ветви параболы направлены вверх, а точка минимума трехчлена ![]() принадлежит отрезку
принадлежит отрезку ![]() .
.
Определяя коэффициенты ![]() из системы
уравнений
из системы
уравнений
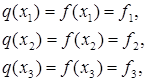
находим:
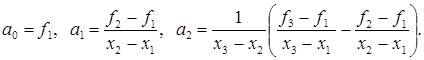
Точку
минимума ![]() квадратного трехчлена
квадратного трехчлена ![]() вычислим, приравняв его
производную к нулю. Получим
вычислим, приравняв его
производную к нулю. Получим
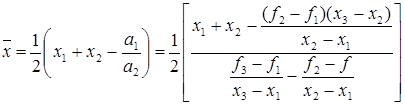 (3.10)
(3.10)
Число
![]() из (3.10) служит очередным
приближением метода парабол к х*. Далее описанная процедура
повторяется для новых точек х1, х2 и х3,
удовлетворяющих неравенству (3.9).
из (3.10) служит очередным
приближением метода парабол к х*. Далее описанная процедура
повторяется для новых точек х1, х2 и х3,
удовлетворяющих неравенству (3.9).
Выбрать
эти точки среди х1, х2, х3
и ![]() можно с помощью перехода от
исходного к новому отрезку
можно с помощью перехода от
исходного к новому отрезку ![]() , содержащему
точку х*, методом исключения отрезков. Для этого перехода
используются пробные точки х2 и
, содержащему
точку х*, методом исключения отрезков. Для этого перехода
используются пробные точки х2 и ![]() и
сравниваются значения f(x) в этих точках. Начало и конец нового
отрезка, а также пробная точка, попавшая в него, образуют тройку точек,
обладающих свойством (3.9).
и
сравниваются значения f(x) в этих точках. Начало и конец нового
отрезка, а также пробная точка, попавшая в него, образуют тройку точек,
обладающих свойством (3.9).
Заметим, что на каждой итерации метода парабол, кроме первой, определяется только одно новое значение f(x).
Условием
окончания поиска служит близость к нулю разности ![]() чисел
чисел
![]() , найденных на данной и предыдущей
итерациях, т.е. неравенство
, найденных на данной и предыдущей
итерациях, т.е. неравенство ![]() , где ε
– заданное число, характеризующее точность определения х*.
, где ε
– заданное число, характеризующее точность определения х*.
Алгоритм метода парабол
Шаг 1. Выбрать точки х1, х2 и х3, удовлетворяющие условиям (3.9). Перейти к шагу 2.
Шаг 2. Найти ![]() по формуле (3.10). На
первой итерации перейти к шагу 4, на остальных – к шагу 3.
по формуле (3.10). На
первой итерации перейти к шагу 4, на остальных – к шагу 3.
Шаг 3. Проверка на окончание поиска. Сравнить модуль разности значений ![]() на данной и предыдущей итерациях
на данной и предыдущей итерациях ![]() с числом
с числом ![]() .
Если
.
Если ![]() , то поиск завершить, полагая
, то поиск завершить, полагая ![]() , иначе перейти к шагу 4.
, иначе перейти к шагу 4.
Шаг 4. Вычислить значение ![]() . Перейти к шагу
5.
. Перейти к шагу
5.
Шаг 5. Определить новую тройку чисел х1, х2 и х3. Присвоить f(х1), f(х2) и f(х3) соответствующие значения f(х), найденные ранее. Перейти к шагу 2.
Пример.
Решить задачу f(x)
= x4 + e-x→min, x![]() [0;1]
с точностью до
[0;1]
с точностью до ![]() =0,0025.
=0,0025.
Итерация 1
Шаг 1. Выберем точки х1 = 0,25, х2 = 0,5 и х3 = 0,75. Функция принимает в этих точках значения соответственно f1 = 0,7817, f2 = 0,6690 и f3 = 0,7888, удовлетворяющие неравенствам (3.9). Переходим к шагу 2.
Шаг
2. По формуле (3.10) находим ![]() = 0,4968.
Переходим к шагу 3.
= 0,4968.
Переходим к шагу 3.
Шаг 3. Вычисляем ![]() = 0,6694. Переходим к
шагу 4.
= 0,6694. Переходим к
шагу 4.
Шаг 4. На данной итерации имеем х1 < ![]() < х2 < х3,
< х2 < х3,
![]() > f(х2),
следовательно,
> f(х2),
следовательно, ![]() . Поэтому полагаем х2
=
. Поэтому полагаем х2
= ![]() =
0,4968, f(х1)
=
=
0,4968, f(х1)
=![]() = 0,6694, а точки х2,
х3 и значения f(х) в
них не изменяются. Переходим к следующей итерации, начиная с шага 2.
= 0,6694, а точки х2,
х3 и значения f(х) в
них не изменяются. Переходим к следующей итерации, начиная с шага 2.
Итерация 2
Шаг
2. Находим ![]() = 0,5224. Переходим к шагу 3.
= 0,5224. Переходим к шагу 3.
Шаг 3. ![]() =
=![]() =
0,026 > 0,0025, поэтому переходим к шагу 4.
=
0,026 > 0,0025, поэтому переходим к шагу 4.
Шаг 4. Вычисляем ![]() =0.6676. Переходим к шагу
5.
=0.6676. Переходим к шагу
5.
Шаг 5. На этой итерации х1 < х2
<![]() < х3, f(х2) >
< х3, f(х2) >![]() ,
поэтому
,
поэтому ![]() , полагаем
, полагаем
х1 = х2 = 0,5, f(х1)
= f(х2)=0,6690, х2
= ![]() = 0,5524, f(х2)
=
= 0,5524, f(х2)
=![]() = 0,6676, а точка х3
и значения f(х3) остаются
прежними. Переходим к следующей итерации.
= 0,6676, а точка х3
и значения f(х3) остаются
прежними. Переходим к следующей итерации.
Итерация 3
Шаг
2. Находим ![]() = 0,5248. Переходим к шагу 3.
= 0,5248. Переходим к шагу 3.
Шаг 3. Определяем ![]() =
=![]() = 0,0024 < 0,0025, т.е.
требуемая точность достигнута. Поэтому полагаем
= 0,0024 < 0,0025, т.е.
требуемая точность достигнута. Поэтому полагаем ![]()
Отметим, что в результате пяти вычислений f(х)
в точке ![]() была найдена с весьма высокой
точностью (сравните с точным до четвертого знака значением
была найдена с весьма высокой
точностью (сравните с точным до четвертого знака значением ![]() = 0,5283).
= 0,5283).
3.5 Метод квадратичной аппроксимации
Метод квадратичной аппроксимации относится к семейству методов полиномиальной аппроксимации. Идея метода полиномиальной аппроксимации состоит в том, что в некоторой окрестности минимума функции f(х) она аппроксимируется полиномом достаточно высокого порядка и в качестве точки минимума функции f(х) (или в качестве очередного приближения к этой точке) принимается точка минимума аппроксимирующего полинома. В силу того, что аппроксимирующая функция является полиномом, этот минимум находится легко.
В качестве аппроксимирующих полиномов чаще всего используются полиномы второго и третьего порядков, т.е. квадратичная и кубическая аппроксимации.
Квадратичная аппроксимация
Рассмотрим квадратичную аппроксимацию (рис. 3.5). Пусть в процессе решения задачи поиска минимума функции f(х) тем или иным образом получены попарно не совпадающие точки х1, х2, х3, принадлежащие области допустимых значений D (не обязательно упорядоченные слева направо).
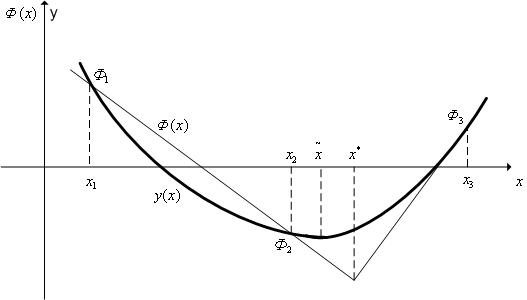
Рис. 3.5. Квадратичная аппроксимация
Построим квадратичную функцию
![]() , (3.11)
, (3.11)
проходящую через точки (хi,fi), где i = 1,2,3, fi = f(хi).
Коэффициенты ![]() функции (3.11)
удовлетворяют системе линейных алгебраических уравнений (СЛАУ)
функции (3.11)
удовлетворяют системе линейных алгебраических уравнений (СЛАУ)
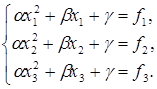 (3.12)
(3.12)
Определитель СЛАУ (3.12) является определителем Вандермонда, который отличен от нуля, если величины х1, х2, х3 попарно различны.
Таким образом, в сделанных предположениях СЛАУ (3.12) имеет решение, и притом единственное. Поскольку определитель СЛАУ (3.12) равен (х1 – х2)(х1 – х3)(х2 – х3), это решение имеет вид:
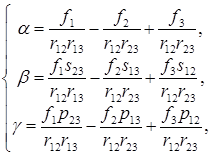
где rij = xi – xj, sij = xi + xj, pij = xi xj.
Подставим
найденные значения коэффициентов ![]() в необходимое
условие
в необходимое
условие ![]() = 0 минимума квадратичной функции
(3.11), получим стационарную точку этой функции
= 0 минимума квадратичной функции
(3.11), получим стационарную точку этой функции
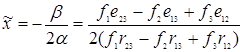 , (3.13)
, (3.13)
где ![]()
Метод квадратичной аппроксимации
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции f(х), определенной на отрезке [a;b]:
![]() (3.14)
(3.14)
Метод квадратичной аппроксимации относится к классу методов сокращения текущего интервала неопределенности (ТИН). Пусть при решении задачи (3.14) каким-либо методом получены три точки х1<х2<х3, принадлежащие области допустимых значений, такие, что f(х1)< f(х2)< f(х3).
Алгоритм метода квадратичной аппроксимации
Шаг 1. Выполняем присваивания ![]() ТИНr = [
ТИНr = [![]() ].
].
Шаг 2. Вычисляем значения ![]() функции f(x) в точках
функции f(x) в точках ![]() соответственно.
соответственно.
Шаг 3. По формуле (3.13) вычисляем величину ![]() и
находим значение функции f(x)
в этой точке
и
находим значение функции f(x)
в этой точке ![]()
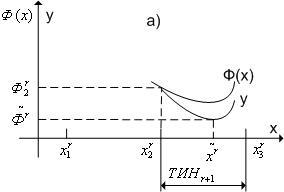
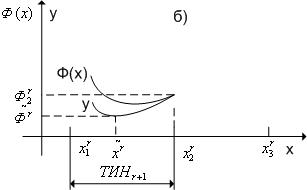
Шаг 4. Находим следующие три точки:
если ![]() , то
, то![]() (рис.
3.6 случай а);
(рис.
3.6 случай а);
если ![]() , то
, то![]() (рис.
3.6 случай б).
(рис.
3.6 случай б).
Шаг 5. В качестве следующего текущего интервала неопределенности
принимаем ТИНr+1 = [![]() ].
].
Шаг 6. Если ![]() , то заканчиваем
вычисления. Иначе выполняем присваивание r = r +
1 и переходим к шагу 2. Здесь
, то заканчиваем
вычисления. Иначе выполняем присваивание r = r +
1 и переходим к шагу 2. Здесь ![]() – требуемая
точность решения.
– требуемая
точность решения.
 |
 |
||
Рис. 3.6. К методу квадратичной аппроксимации
В качестве приближенного значения точки минимума х* с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Замечание
В силу условий ![]() точка
точка ![]() всегда принадлежит текущему
интервалу неопределенности ТИНr =
всегда принадлежит текущему
интервалу неопределенности ТИНr = ![]() .
.
3.6 Метод Паулла
Данный метод относится к классу методов квадратичной аппроксимации, которые, в свою очередь, относятся к семейству методов полиномиальной аппроксимации. В качестве аппроксимирующего полинома в этом случае используется квадратичный полином. Метод используется для решения одномерных задач безусловной оптимизации – задач поиска минимума одномерных унимодальных функций в области допустимых значений (– ∞,∞).
Рассмотрим следующую задачу безусловной оптимизации (если ограничения на вектор варьируемых переменных X отсутствуют, то детерминированная задача оптимизации называется задачей безусловной оптимизации): найти минимум одномерной унимодальной функции f(x), определенной в незамкнутой области допустимых значений D(–∞,∞),
![]() (3.15)
(3.15)
Алгоритм метода Паулла
Шаг 1. Полагаем r =
1 и задаем начальную точку ![]() .
.
Шаг 2. Находим точку ![]() , где Δ –
длина шага, которая должна быть величиной того же порядка, что и расстояние
точки
, где Δ –
длина шага, которая должна быть величиной того же порядка, что и расстояние
точки ![]() до точки минимума функции f(x) (оценка этого
расстояния является самостоятельной проблемой).
до точки минимума функции f(x) (оценка этого
расстояния является самостоятельной проблемой).
Шаг 3. Вычисляем значения ![]() , функции f(x) в точках
, функции f(x) в точках ![]() .
.
Шаг 4. Находим точку 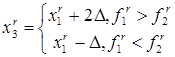 .
.
Шаг 5. Вычисляем значение ![]() функции f(x) в точке
функции f(x) в точке ![]() (рис. 3.7).
(рис. 3.7).
Шаг 6. По формуле (3.13) вычисляем величину ![]() и
находим значение функции f(x)
в этой точке
и
находим значение функции f(x)
в этой точке ![]() .
.
Шаг 7. Находим следующие три точки:
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]()
если ![]() , то
, то ![]() (рис.
3.8, случай в);
(рис.
3.8, случай в);
если ![]() , то
, то ![]() (рис.
3.8 случай г).
(рис.
3.8 случай г).
Шаг 8. В качестве следующего текущего интервала неопределенности
принимаем ТИНr+1 = ![]() .
.
Шаг 9. Если ![]() , то заканчиваем
вычисления. Иначе выполняем присваивание r = r +
1 и переходим к шагу 6. Здесь
, то заканчиваем
вычисления. Иначе выполняем присваивание r = r +
1 и переходим к шагу 6. Здесь ![]() – требуемая
точность решения.
– требуемая
точность решения.
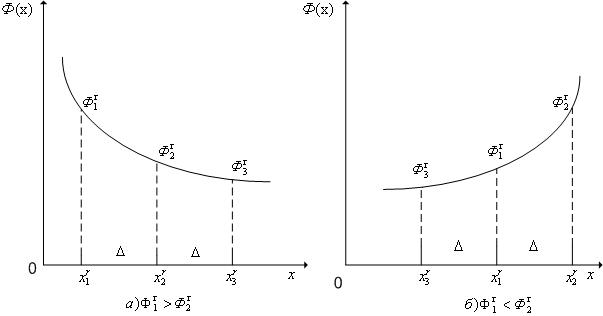
Рис. 3.7. К
определению точки ![]()
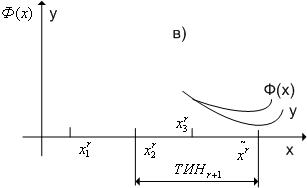
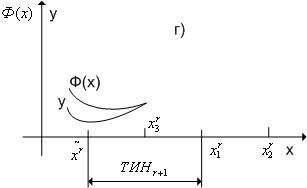
Рис. 3.8. Случаи ![]() и
и ![]()
В качестве приближенного значения точки минимума х* с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.