"Когда и как люди научились считать и записывать числа?"

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №8

города Красноармейска Саратовской области»

Как и когда люди научились считать и записывать числа?

Авторы работы: обучающиеся 6 «Б» класса

Костина Анна,

Пахомов Антон,

Зуев Антон,

Кудряшов Дмитрий.

Руководитель:

Борисова Антонина Владимировна-

учитель математики.

2009 год

город Красноармейск

Саратовская область

ОГЛАВЛЕНИЕ

1.     Введение……………………………………………………………...3

2.     Как люди научились считать………………………………………..4

3.     Как люди научились записывать цифры и числа………………….7

             3.1.Древний Египет……………………………………………………..7

             3.2.Древний  Вавилон…………………………………………………..9

             3.3.Индия………………………………………………………………..11

             3.4.Рим…………………………………………………………………..12

             3.5.Алфавитные системы  счисления…………………………………13

4.     Заключение…………………………………………………………..16

5.     Список используемой литературы…………………………………17

6.     Приложения………………………………………………………….18

1.     Введение

Сколько тебе лет? Сколько у тебя друзей? Сколько лап у кота? Чтобы все подсчитать, нужно знать цифры. А как считали древние люди, которые их не знали? А как считали и записывали цифры и числа люди, жившие в более позднее время в Древнем Египте, Вавилоне, Индии и в других странах? Эти вопросы и подвигли нас к тому, чтобы заняться исследовательской деятельностью и понять, связаны ли наши современные представления о числе и счете с теми знаниями, которыми обладали наши далекие предки.

2.     Как люди научились считать?

.Давным-давно, многие тысячи лет назад, наши далекие предки жили небольшими племенами. Они бродили по полям и лесам, по долинам рек и ручьев, разыскивая себе пищу. Питались листьями, плодами и корнями  различных растений. Иногда ловили рыбу, собирали ракушки или охотились. Одевались в шкуры убитых зверей. Жизнь первобытных людей мало чем отличалась от жизни животных. Да и сами люди отличались от животных только тем, что владели речью и умели пользоваться простейшими орудиями труда: палкой, камнем или камнем, привязанным к палке.

Первобытные люди, так же как и современные маленькие дети, не знали счета. Но теперь детей учат считать родители и учителя, старшие братья и сестры, товарищи. А первобытным людям не у кого было учиться. Их учителем была сама жизнь. Поэтому и обучение шло медленно.

Наблюдая окружающую природу, от которой полностью зависела его жизнь, наш далекий предок из множества различных предметов сначала научился выделять отдельные предметы. Из стаи волков - вожака стаи, из стада оленей - одного оленя, из выводка плавающих уток - одну птицу, из колоса с зернами - одно зерно.

Поначалу они определяли это соотношение как "один" и "много".

Частые наблюдения множеств, состоявших из пары предметов (глаза, уши, рога, крылья, руки), привели человека к представлению о числе. Наш далекий предок, рассказывая о том, что видел двух уток, сравнивал их с парой глаз. А если он видел их больше, то говорил: "Много". Лишь постепенно человек научился выделять три предмета, ну а затем четыре, пять, шесть и т. д.

Учиться считать требовала жизнь. Добывая пищу, людям приходилось охотиться на крупных зверей: лося, медведя, зубра. Охотились наши предки большими группами, иногда всем племенем. Чтобы охота была удачной, нужно было уметь окружить зверя. Обычно старший ставил двух охотников за берлогой медведя, четырех с рогатинами -- против берлоги, трех - с одной стороны и трех - с другой стороны берлоги. Для этого он должен был уметь считать, а так как названий чисел тогда еще не было, он показывал число на пальцах.  Пальцы сыграли немалую роль в истории счета, особенно когда люди начали обмениваться друг с другом предметами своего труда. Так, например, желая обменять сделанное им копье с каменным наконечником на пять шкурок для одежды, человек клал на землю свою руку и показывал, что против каждого пальца его руки нужно положить шкурку. Одна пятерня означала 5, две- 10. Когда рук не хватало, в ход шли и ноги. Две руки и одна нога - 15, две руки и две ноги - 20.

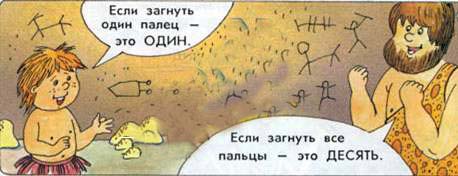
Следы счета на пальцах сохранились во многих странах. Так, в Китае и Японии предметы домашнего обихода (чашки, тарелки и др.) считают не дюжинами(по12 штук) и полудюжинами, а пятерками и десятками. Во Франции и в Англии и поныне в ходу счет двадцатками.

Специальные названия чисел имелись - поначалу только для одного и двух. Числа же больше двух называли с помощью сложения: 3 - это два и один, 4 - это два да два, 5 - это два, еще два и один.

Названия чисел - у многих народов указывают на  их происхождение.

Так, у индейцев два  -  глаза, у тибетцев - крылья, у других народов один - луна, пять - рука и т. д.  У тех народов, которые еще сохранили первобытный уклад жизни, такие названия чисел используются до сих пор. Например, у одного из австралийских племен счет ведется так:

1 - энэа,                             2 - петчевал,

3 - петчевал-энэа,             4 - петчевал-петчевал.

А в другом племени считали так:

1 - мал,        2 - булан,                 3 - гулиба,

                     4 - булан-булан,     5 - булан-гулиба,  

                                                      6 - гулиба-гулиба.

А на берегах реки Амазонки было обнаружено племя, которое знало только три числа- 1, 2 и 3, причем число 3 называлось "поэттаррароринкоароак". Вот как трудно было людям научиться считать!

3.Как люди научились записывать цифры и числа?

В разных странах и в разные времена это делалось по-разному. Когда люди не умели еще делать бумагу, записи появлялись в виде зарубок на палках и костях животных, в виде отложенных ракушек или камешков или в виде узелков, завязанных на ремне или веревке.

3.1.Древний Египет

В Древнем Египте числа первого десятка записывали соответствующим количеством палочек. А "десять" обозначалось скобочкой в виде подковы. Чтобы написать 15, надо было ставить 5 палочек и 1 подкову. И так до сотни. Для сотни придуман был крючок, для тысячи - значок вроде цветка. Десять тысяч обозначали рисунком пальца, сто тысяч - лягушкой, а миллион -  фигуркой с поднятыми руками. Не очень-то удобно было записывать таким способом большие числа и совсем неудобно было их складывать, вычитать, умножать, делить. Очень большая возня была с этими значками-иероглифами!

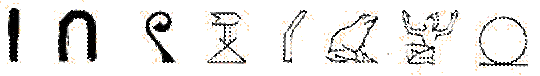
      Так, например, с помощью коллективных символов и повторений уже введенных символов число   6789 в иероглифических обозначениях можно было бы записать как

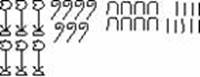
Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.)

 и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетской арифметике и геометрии.

3.2. Древний Вавилон.

Гораздо лучше придумали запись чисел в древнем Вавилоне.

Первой известной нам позиционной системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2500—2000 лет до н. э. Основанием ее служило число 60. Следовательно, в ней 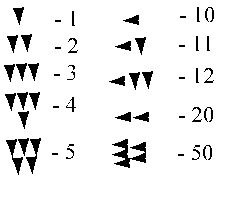должно было бы быть 60 цифр.

Вавилоняне поступали так: записывали все числа от 1 до 59 по десятичной системе, применяя принцип сложения. При этом они пользовались всегда двумя знаками: прямым клином  для обозначения 1 и лежачим клином  для 10. Число 32, например, писали так:

Эти знаки и служили цифрами в их системе. Число 60 снова обозначалось тем же знаком, что и 1, т. е. .Так же обозначались и числа 3600, 60³ и все другие степени 60. Например, число 92 записывали так:

 Она очень похожа на современную,  только мы считаем десятками, сотнями, тысячами и так далее, а жители древнего Вавилона объединяли единицы по 60, по 3600 (60x60=3600), а если надо, по 60x60x60=216000 и так далее. Писали в древнем Вавилоне на мягких глиняных табличках острыми палочками, а потом таблички обжигали, и они становились твердыми и прочными. При раскопках были найдены целые библиотеки и архивы из таких табличек.

Квадрат с диагоналями. Древневавилонский    клинописный текст. (Из коллекции Йельского 

 университета)

Шестидесятеричная система вавилонян сыграла большую роль в развитии математики и астрономии. Следы ее сохранились до наших дней. Так, мы до сих пор делим час на 60 минут, а минуту на 60 секунд. Точно так же, следуя примеру вавилонян, окружность мы делим на 360 равных частей (градусов).

3.3. Индия

А вот система нумерации и вычислений, которая сложилась в Индии примерно к VI веку нашей эры, оказалась такой удобной и удачной, что ею сейчас пользуются во всем мире. Европейцы познакомились с ней в X - XIII веках через арабов, которые первыми оценили достоинства этого способа записи чисел, усвоили и перенесли в Европу, поэтому новые цифры в Европе стали называть арабскими. Произошло это еще и потому, что простейший счетный прибор, работающий в десятичной системе счисления, был всегда у человека под рукой - это его 10 пальцев.

Вначале индийских цифр было всего 9:1,2,3, 4, 5, 6, 7, 8 и 9. Цифра 0 появилась заметно позже, - скорее всего, около 500 года нашей эры. А поначалу, если оказывалось, что в каком-то разряде нет единиц, то между соседними разрядами оставляли пробел. Например, число 209 писали так: 2 9. Понятно, что при подсчете таких пробелов очень легко ошибиться. Чтобы избавиться от этих неприятностей, сначала вместо пустого разряда стали ставить точку, а потом - маленький кружочек, который постепенно превратился в цифру 0.

Форма индийских цифр претерпевала многообразные изменения. Та форма, в которой мы их пишем, установилась в 16 веке.

Вот, оказывается, какая длинная история у этих знакомых значков!

Значительно позднее цифры стали изображать иначе.

Из арабского языка заимствовано и слово «цифра» (по-арабски «сыфр»), означающее буквально «пустое место» (перевод санскритского слова «сунья», имеющего тот же смысл).

3.4.Рим.

 Вот посмотрите Римскую нумерацию: I - один, II - два, III - три. На руке человека пять пальцев. Чтобы не писать пять палочек, стали изображать руку.

Однако рисунок руки делали очень простым. Вместо того чтобы рисовать всю руку, ее изображали знаком V, и этот значок стал обозначать цифру 5. Потом к пяти прибавляли один и получали шесть. Вот так: шесть - VI, семь - VII. А сколько записано здесь: VIII? Правильно, восемь. Ну а как короче записать четыре? Четыре палочки долго пересчитывать, поэтому от пяти отнимали один и записывали так: IV - это пять без одного.

А как записать десять?

Вы знаете, что десять состоит из двух пятерок, поэтому в римской нумерации цифру "десять" изображали двумя пятерками: одна пятерка стоит как обычно, а другая перевернута вниз - X. Иначе десять можно записать двумя пересекающимися палочками. Если рядом с X написать одну палочку справа - XI, то будет одиннадцать, а если слева - IX - девять.

Запомните особенность римской записи: меньшая цифра, стоящая справа от большей, прибавляется к ней, стоящая слева - отнимается. Поэтому знак VI означает 5+1, то есть 6, а знак IV -5-1, то есть 4. Научиться читать числа, записанные в римской нумерации, нетрудно, и мы советуем это сделать обязательно. Позднее появились значки и для обозначения других чисел. Так 100 стали обозначать буквой С (первая буква соответствующего латинского слова - centum), число 1000 - буквой М (mille - тысяча), число 500 - буквой D, буквой L - число 50.

Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 века, а в других странах Западной Европы—до 16 века.

    Мы пользуемся ею для обозначения юбилейных дат, для наименования съездов и   конференций, для нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т. д.

3.5. Алфавитные системы счисления

Когда возникла письменность, многие народы начали для обозначения чисел использовать алфавит.

Алфавитная система счисления была распространена у древних армян, грузин, греков (ионическая система счисления), арабов, евреев, славян и других народов.

Для того, чтобы отличать числа от слов, над буквами, изображающими числа, ставили специальный значок: греки - просто черточку, а славяне - волну, которая называлась "титло".

Алфавитная система была принята и в древней Руси.

Удобны ли алфавитные системы?

Запишем в славянской нумерации число 444:

Мы видим, что запись получилась не длиннее нашей. Это объясняется тем, что в алфавитных нумерациях имелось 27 цифр, тогда как в египетской, например, для обозначения всех чисел до 1000 было всего лишь три цифры.

Но алфавитные нумерации имели и крупный недостаток: с их помощью нельзя обозначать сколь угодно большие числа. Они были удобны только для записи чисел до 1000.

Правда, славяне, как и греки, умели записывать и большие числа, но для этого к алфавитной системе добавляли новые обозначения. Числа 1000, 2000 и т. д. они записывали теми же буквами, что 1, 2 и т. д., только слева внизу ставился специальный знак  , например 1000 обозначали . Аналогично:

 
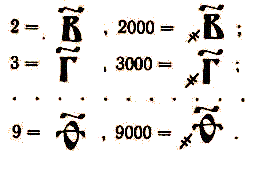
Число 10000 опять обозначалось той же буквой, что и 1, только без титла, но его уже обводили кружком:

10000= . Называлось это число "тьмой". Отсюда, между прочим, произошло выражение "тьма народу".

Итак, для обозначения тем первые 9 цифр обводились кружками:

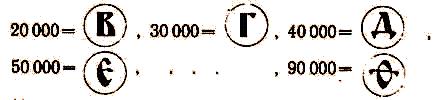
10 тем, или 100000, было единицей высшего разряда. Ее называли "легион". В записи вокруг первых

9 цифр ставился кружок из точек:

100000=  , 200000=  и т. д.

10 легионов составляли новую единицу, которая называлась "леодр". Для обозначения леодров соответствующие числа заключали в кружок из черточек:

1000000= , 2000000=  и т. д.

Эти обозначения можно рассматривать как зачатки позиционной системы, так как в ней для обозначения единиц разных разрядов применялись одни и те же символы, к которым добавлялись знаки для определения разряда. Такая система называлась малым числом. В ней обозначения не шли дальше миллионов.

Но наряду с этим имелось и "большое", или "великое", число, в котором словом "тьма" обозначался уже миллион. Тьма тем (т. е. 10¹²) называлась легионом, легион легионов (т. е. 10²⁴) — леодром, леодр леодров (т. е. 10⁴⁸) — "вороном", и, наконец, число 10⁴⁹ называлось "колодой". В рукописи XVII в. говорится: "И более сего несть человеческому уму разумевати", т. е. для больших чисел уже нет названий. Для обозначения воронов буквы ставили в кружок из крестиков: 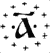, а колоду обозначали так: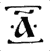 

Алфавитные нумерации, как мы говорили, были мало пригодны для оперирования с большими числами, встречавшимися уже в древности (например, при астрономических расчетах). В ходе развития человеческого общества эти системы уступили место позиционным. Но остатки алфавитных нумераций сохранились в нашем обиходе и по сей день. Так, мы часто нумеруем пункты при помощи букв алфавита. Правда, буквы служат только для обозначения последовательного порядка, а не количества. Никаких арифметических операций над такими буквами мы уже не производим.

Славянская система счисления сохранилась в богослужебных книгах.

4.     Заключение

1)    Рассмотрев различные системы счисления, существовавшие в древности, мы пришли к выводу, что все знания в этой области оставили свой отпечаток на современных представлениях о формах записи чисел и о числе вообще. Но нам кажется, что наиболее близкой и понятной школьникам является десятичная система счисления, прообразом которой является  древнеиндийская система нумерации и вычислений.

2)    Мы выявили, что современные люди пользуются десятичной системой счёта, потому что у человека на руках 10 пальцев.

3)    Система счета, которую мы используем сегодня, была изобретена в           Индии тысячу лет назад. Арабские купцы распространили ее по всей Европе к 900 году. В этой системе использовались цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0. Это десятичная система, построенная на основе десятки.

4)     Полученные знания мы будем использовать в дальнейшем на уроках математики и информатики. А также будем дальше стараться «открыть» еще какие-либо «секреты», которые связаны с числами.

5.     Литература и источники.

    Депман И.Я.,  Виленкин Н.Я. За страницами учебника матема-    тики. – М.: Просвещение, 1989.

    Крейг А. и  Росни К. Наука. Энциклопедия. – М.: «Росмэн», 1994.

    Математика: Учебник-собеседник для 5-6 классов средней школы /     Шаврин Л.Н.,  Гейн А.Г.,  Коряков И.О., М.В. Волков М.В.М.: 

    Просвещение, 1989.

    Ризванова Х.Я. Книга для внеклассного чтения по математике.  – Уфа: Китап, 1998.

    Шпорер З. Ох, эта математика! – М.: Педагогика, 1985.

    Энциклопедический словарь юного математика / Сост. Савин А.П. – М.: Педагогика, 1989.

     История развития математики.

     http://evolutsia.com/content/view/730/41/

    Олехник С.Н., Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи.- М.: АО «Столетие», 1994.

    Глейзер Г.И. История математики в школе.- М.:Просвещение,1981.

    Депман И.Я., Виленкин Н.Я. За страницами учебника математики.- М.: Просвещение, 1989.

    Занимательные рассказы о математике: Сост.: Смирнов Ю.И.-СПб.: ИКФ «МиМ-Экспресс»,1995.

    Легдон Н., Снейт Ч. С математикой в путь.- М.: Педагогика, 1987.

Скачано с www.znanio.ru