КОЛЛЕКТИВНАЯ УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ УМЕЕМ ЛИ?

РЕГИОНАЛЬНЫЙ МАСТЕР-КЛАСС ПЕДАГОГИЧЕСКИХ РАБОТНИКОВ

«АКТИВНЫЕ МЕТОДЫ ОБУЧЕНИЯ И ВОСПИТАНИЯ КАК СПОСОБ ПОВЫШЕНИЯ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ СТУДЕНТОВ

В СИСТЕМЕ СПО»

ТЕМА РАБОТЫ Коллективная учебная деятельность

Шкурина Надежда Анатольевна, преподаватель

КГБПОУ «Техникум горных разработок имени В. П. Астафьева»

КОЛЛЕКТИВНАЯ УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ УМЕЕМ ЛИ?

УМЕЕМ ЛИ?

Во что зачастую превращается совместное творчество группы взрослых людей? Кто не знает ответа на этот вопрос — пусть включит телевизор. И что же он увидит? А увидит он: неумение слушать и слышать; неумение спорить тактично; агрессивную реакцию на критику...

Что же мешает? Да ведь люди просто не умеют работать коллективно! Ну, не учили их, не было принято... И учить поздновато. А мы давайте сделаем то, что можем, — научим детей коллективному сотворчеству, решению задач сообща.

ФАКТОР УСПЕХА

Что больше всего влияет на успеваемость? Квалификация педагога? Затраты на обучение? Уровень развития обучающихся? Или, скажем, количество книг в библиотеке техникума? Как бы ответили на этот вопрос вы?

Результаты грандиозного исследования американского социолога Коумена Джеймса оказались однозначными. Все важно: и квалификация педагога, и оборудование кабинетов... Но больше всего — группа! Развитие товарищей в группе, их успеваемость и жизненные планы по большому счету важнее, чем затраты средств на одного обучающегося, число обучающихся в группе, количество книг в библиотеке и даже квалификация педагога.

В умело организованном коллективе каждый работает на каждого. Дело педагога за "малым" — помочь обучающимся умело организоваться на своих уроках. Наверное, в этом и кроется секрет лучших педагогов, умеющих СОЗДАТЬ КЛАСС.

СТАРОЕ СТАНОВИТСЯ НОВЫМ

Многие уже знакомые нам гаммы педагогической партитуры звучат иначе при переходе от соло к ансамблю. Речь идет о работе в группах. Группа может быть от 2 до 12 обучающихся. Впрочем, верхняя граница весьма условна. Но для большинства форм предлагаемой групповой работы оптимальна группа из 4 обучающихся.

ОРГАНИЗАЦИЯ РАБОТЫ В ГРУППАХ

СХЕМА 1

ФОРМУЛА: группы получают одно и то же задание.

В зависимости от типа задания результат работы группы может быть или представлен на проверку преподавателю, или спикер одной из групп раскрывает результаты работы, а другие обучающиеся его дополняют или опровергают.

Пример. Ученики еще не знают, что речь идет о понятии из физики "плотность". Группам раздаются куски пластилина с указанием измерить массу и объем как можно точнее. У каждой группы — свой кусок, отличающийся величиной. По мере выполнения работы группы заносят результат в таблицу. Всегда находятся группы, допустившие ошибки. Поэтому таблица выглядит примерно так:

Преподаватель: — Вот общая таблица результатов. Посмотрите на нее внимательно. Какие можно сделать выводы? Можно ли, не перепроверяя все измерения, определить, кто ошибся?

В обсуждение включаются все. Через некоторое время озарение: у всех первая цифра больше второй, а у третьей группы меньше! А нельзя ли найти более точное соотношение между цифрами? Группы работают: прибавляют, отнимают, делят... Наконец, возникает смутная догадка: масса, деленная на объем, дает число, примерно одинаковое почти у всех групп. Проверка показывает, что это соотношение отличается сильно только у третьей и седьмой групп. Эти группы проделывают опыт повторно и убеждаются, что и их пластилин подчиняется тому же соотношению. Вот теперь обучающиеся догадываются о понятии "плотность".

СХЕМА 2

ФОРМУЛА: группы получают разные задания.

Тогда группы (или их спикеры) отчитываются перед классом. Или, поочередно меняясь, спикеры по кругу обходят все группы и работают с каждой.

Пример. Одна группа готовит опорный сигнал с докладом по теме повторения. Другая делает разбор нескольких задач по этой же теме. Третья и четвертая заняты подобным же образом, но по другой теме. По завершении работы спикеры каждой группы обходят по очереди остальные группы с докладами. Таким образом, на одном занятии повторяется несколько тем разными способами.

СХЕМА 3

ФОРМУЛА: группы получают разные, но работающие на общий результат задания.

Пример. Каждая группа определяет плотность какого-либо минерала, после чего результаты сводятся на доске в единую таблицу. Психологический сверхэффект: обучающиеся очень гордятся, когда результат их работы оказывается нужным всему классу. А преподаватель использует это и не раз еще обратится к полученной таблице.

ЛОВИ ОШИБКУ!

ФОРМУЛА: ребята ищут ошибку группой, спорят, совещаются... Придя к определенному мнению, группа выбирает спикера. Спикер передает результаты преподавателю или оглашает задание и результат его решения перед всем классом.

Чтобы обсуждение не затянулось, заранее определите для него время.

Пример. Преподаватель дает серию формул или формулировок, среди которых есть как правильные, так и неправильные. Задача группы — найти неправильные, доказать их неверность и заменить правильными. Вот неправильное определение: "Прибор, позволяющий установить поверхность горизонтально, называют уровнем". В результате работы ребята заменяют его на такое: "Прибор, позволяющий установить горизонтальность поверхности, называют уровнем".

Конечно, данные примеры не исчерпывают всех вариантов применения приема. Группы могут получать разборы задач или примеров со смысловыми ошибками, тексты с ошибками, чертежи или рисунки с ошибками... Есть где развернуться фантазии преподавателя.

ОТКРЫТАЯ ПРОБЛЕМА: к сожалению, практически нет готового дидактического материала к этому приему. Нет сомнений, что со временем найдутся авторы и такой материал по разным предметам будет создан. Может быть, вы и займетесь разработкой?

ПРЕСС - КОНФЕРЕНЦИЯ И ВОПРОС К ТЕКСТУ

ФОРМУЛА: обучающиеся составляют списки вопросов, разбившись по группам.

Группы могут работать над одним и тем же текстом (или частью лекции), но одни из них — над репродуктивными вопросами, другие — над расширяющими или развивающими. Можно иначе: группы работают над разными частями текста или лекции.

СВОЯ ОПОРА

ФОРМУЛА 1: группа составляет опорный конспект урока или темы на листе большого формата.

ФОРМУЛА 2: несколько сильных обучающихся заранее получают творческое д/з: составить опорные конспекты по различным когда-то пройденным темам. На одном из занятия они становятся тренерами. Группа разбивается на подгруппы, с каждой из них работает такой тренер по своему опорному конспекту.

После работы в отведенное время над определенной темой тренеры меняют группы, и процесс повторяется. Важно: группы должны получать от тренеров какое - то задание. Например, составить список вопросов по повторяемому конспекту, или найти ошибку, которая заранее специально внесена в конспект, или...

Мастер – класс по теме: «Показательная функция».

Цели мастер – класса

Обучающая: Сформировать понятие показательной функции, рассмотреть ее свойства и график, рассмотреть задачи по данной теме; предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.

Развивающая: способствовать развитию памяти, внимания, навыков самооценки и самоконтроля; формированию таких ключевых компетенций, как сравнение, сопоставление, классификация объектов, определение адекватных способов решения учебной задачи на основе заданных алгоритмов, способность самостоятельно действовать в ситуации неопределённости, контролировать и оценивать свою деятельность, находить и устранять причины возникших трудностей.

Воспитательная: развивать у обучающихся коммуникативные компетенции (культуру общения, умение работать в парах); способствовать воспитанию воли и упорства для достижения конечных результатов.

Технологии: индивидуально–дифференцированного обучения, ИКТ.

Методы обучения: словесный, наглядный, практический, проблемный.

Формы работы: индивидуальная, фронтальная, в парах.

Оборудование и материалы для урока: проектор, экран, ПК для каждого ученика, видеолекция (Приложение №1),презентация (Приложение №2),индивидуально – дифференцированные карточки для самостоятельной работы в парах (Приложение №3) , индивидуально-дифференцированное  домашнее задание (Приложение №4), интерактивный тест (Приложение №5).

Данный мастер – класс проводится с целью подготовки к итоговой аттестации по теме «Корни, степени и логарифмы» и  применение его при решении экзаменационных задач.

Продолжительность мастер – класса – 30 мин.

Структура мастер - класса

         I. Организационный момент.

II. Сообщение темы, цели мастер - класса, мотивация учебной деятельности.

III. Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач.

IV. Проверка  индивидуального задания. Тестирование. Анализ результатов тестирования.

V. Защита индивидуального задания.

VI. Индивидуально – дифференцированное домашнее задание.

VII. Оценки за урок.

VIII. Рефлексия.

Ход  мастер - класса

I. Организационный момент.

II. Сообщение темы, целей мастер - класса, мотивация учебной деятельности.

Тема нашего мастер-класса «Показательная функция».

Мы познакомимся с понятием показательной функции, рассмотрим ее свойства и график, задачи по данной теме, проверим знания при самостоятельном решении задач. В конце занятия мы вернёмся к цели нашего мастер-класса и выясним, достигли ли её?

Применим теоретические знания для решения практических задач.

Актуализация знаний

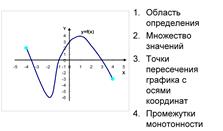Функция – основной математический инструмент для изучения связей, зависимостей между различными величинами. Чем большим запасом функций мы располагаем, тем шире и богаче наши возможности математического описания окружающего мира.

• Какие функции вам известны?

Линейная функция, описывает, например, равномерное прямолинейное движение;

Квадратичная функция – описывает движение с ускорением;

Обратная пропорциональность – описывает, например, зависимость объема, занимаемого газом, от его плотности.

• Какие свойства функций вам известны?

1. Область определения
2. Множество значений
3. Точки пересечения графика с осями координат
4. Промежутки монотонности

 Изучение новой темы

Ученые-биологи, изучая жизнь бактерий, установили, что рост числа бактерий происходит по формуле N=5^t, где N-число колоний бактерий в момент времени t, t- время размножения

Вычислите, как изменится число колоний бактерий за 2 секунды? (увеличится до 25). За 3 секунды? (увеличится до 125). Т.е. каждому моменту времени соответствует свое определенное число бактерий.

 Зависимость такого типа между двумя переменными была замечена не только в процессе роста числа микроорганизмов, но и, например, в спорте – зависимость длины прыжка спортсмена с трамплина от начальной скорости полета, в медицине – способность почек выводить из крови радиоактивные изотопы, в предвыборных кампаниях.

В рамках предвыборной кампании каждый кандидат выбирает себе в помощники двух доверенных лиц. Каждый из доверенных лиц в течение следующего дня, проводя агитационную работу, привлекает в команду этого кандидата еще по одному человеку. На следующий день агитационная работа проводится уже командой в 4 человека. Что произойдет с командой кандидата, если эту работу продолжить по той же схеме? Команда кандидата будет очень быстро расти.

Для зависимостей данного вида составлена следующая математическая модель: y = a^x.

Я предлагаю вам сегодня на уроке исследовать эту математическую модель.

• Что значит “изучить функцию”?

Изучить функцию, значит, дать ее определение, рассмотреть свойства и построить график. Это и есть цели нашего сегодняшнего мастер-класса.

III. Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач.

Займите компьютеры. Обучающиеся получают тестовое задание. Изучают материал презентации или видеоурока отвечают на вопросы. Результаты исследований записывают в тетрадь.

IV. Проверка  индивидуального задания.

Тестирование. Анализ результатов тестирования.

- Кто испытывал трудность при тестировании?

 - Кто не допустил ошибок?

V. Защита индивидуального задания.

Обучающимся задаются вопросы по тесту.

VI. Индивидуально – дифференцированное домашнее задание.

Решить  задания по вариантам.

VII. Оценки за урок

VIII. Рефлексия.

- Подведем итог. Какова была цель мастер-класса? Как вы считаете, достигнута ли  она?

- Какая функция называется показательной?

- Назовите свойства показательной функции для а > 1 и 0 < a < 1.

- Какие свойства функции являются общими для этих двух случаев?

Посмотрите на доску и одним предложением, выбирая начало фразы, продолжите предложение, которое вам больше всего подходит. Я почувствовал…

Я  научился…

У меня получилось …

Я смог…

              Я попробую …

              Меня удивило, что …

              Мне захотелось…

А закончить мастер-класс я хотела бы словами итальянского философа Фомы Аквинского «Знание – столь  драгоценная вещь, что его не зазорно добывать из любого источника».

Список источников:

1. А. Гин. Приемы педагогической техники, - пособия для учителя, 15-изд. Издательство «Вита», Москва, 2018.