
A.K.Yusupova. A.A.Abdumanonovh
![]()
![]() KOMBINATORIKA
KOMBINATORIKA![]()
GRAFIAR NAZARIYASI

O'ZBEKISTON RESPUBLIKASI OLIY VA ORTA TA'LIM VAZIRLIGI
O'ZBEKISTON RESPUBLIKASI SOG'LIQNI SAQLASII VAZIRLIGI
FARG'ONA JAMOAT SALOMATLIGI TIBBIYOT
INSTITUTI![]()
A.K.Yusupova, A.A.Abdumanonov
GRAFLAR NAZARIYASI
O ':bekiston Respublikasi Oliy va o 'Ha ta Tim vazirligi tomonida Biotibbiyot muhandis/igi bakalavriat ta 'lun yo "nalishi talaba/ari uchun
darslik sifatida Íavsiya etilgan
UOS K: 68ya73
KBK:![]()
Y 91
Kombinatorika va graglar nazariyasi / darslik:
![]() T,: "Classic" , 2022-yil, —300 bet,
T,: "Classic" , 2022-yil, —300 bet,
Mazkur darslik kombinatorika va graglar nazariyasi
TAQRIZCHILAR:
FJSTI o'quv ishlari bo'yicha prorektor PhD
M.T.Botirov
TATUFF Axbrott trxnologiyalari
kafedrasi professori, fizika matematika fanlari nomzodi![]()
D.A.Xali10v![]()
Ta'lijn 60711800 — Biotibbjyoer mnhandisligl.
O'zbekiston Respub/ikasi Oliy va o 'rta maxsus ta'/im vazir/igining
2022
yil "17" mart dagi "106" — sonli buyrag![]()
ISBN: 978-9943-8247-1-3
© ![]() 2022
2022
C' "Classic" nashiryoti, 2022
scyz
BOSHI![]()
Matematik fanlar zamonaviy madaniyatning tarkibiy qismi bo'lgani va tibbiyot yo'nalishlari uchun kerakli fan bo•łgani uchun, tibbiyot yo•nalishlari o'quv rejasiga ham matematika fani kiritilgan.
Hozirgi vaqtda matematik usullarining
barcha sohalarga kirib borishi har bir kasb egasidan matematika asoslarini
yaxshi bilishni talab etmoqdaKombinatorika va graflar nazariyasi matematikaning
bir qismi bo'lib ![]() ushbu fan doirasida ko'plab amaliy
masalalar o'rganiladi. Fan doirasida o'rganilgan bilimlar tadqiqot ishlarida,
amaliy va nazariy tibbiyotning turli jabhalarida, shuningdek, ta'lim tizimida
qo'llanilishi mumkin.
ushbu fan doirasida ko'plab amaliy
masalalar o'rganiladi. Fan doirasida o'rganilgan bilimlar tadqiqot ishlarida,
amaliy va nazariy tibbiyotning turli jabhalarida, shuningdek, ta'lim tizimida
qo'llanilishi mumkin.
Ushbu darslik tibbiyot institutlari biotibbiyot muhandisligi bakalavr yo•nalishlari talabalariga mo'ljallangan bo'lib, darslik "Kombinatorika va graflar nazariyasi” namunaviy dasturiga asoslanib yozilgan,
Darslikdan talabalar, magistrantlar va shu sohaga qiziqqanlar foydalanishlari mumkin,
ı BOB. "KOMBİNATORIKA VA GRAFLAR NAZARIYASI”
FANINING MAZMUNI, PREDMETI VA METODİ
1.1-ŞMatematikaning zanıonaviy dunyoda jahon madaniyati va tarixida, jıımladan tibbiyot sohasida tutgan o'rni
Zamonaviy shifokor kompyuter
texnologiyalarini juda yaxshi bilishi zarur, U bemorga tashxis qo'yar ckan,
bunda laboratoriya va kompyutcr ![]() texnologiyalari natijalarini tahlil
qilishi, ya'ni son ko'rsatkichlari va sifat ko'rsatkichlari orasidagi
bog'lanishni juda katta aniqlikda topishi talab eliladi. Shifokor inson
organizmida kechayolgan kimyoviy va fizik jarajonlarni kuzala olishi, ya'ni bu
jarayonlar qaysi tomonga qarab borayotganligini, qanday sur'atlarda
borayotganligini his qilishi lozimBu jarayonlarni tadqiq qilish esa
matematikasiz mumkin emas. Bunda malamalik lalTakkurning, malamalik maniiqning,
matematik indüksiya, dedüksiya va silil kabilarning o'rni bcqiyos,
texnologiyalari natijalarini tahlil
qilishi, ya'ni son ko'rsatkichlari va sifat ko'rsatkichlari orasidagi
bog'lanishni juda katta aniqlikda topishi talab eliladi. Shifokor inson
organizmida kechayolgan kimyoviy va fizik jarajonlarni kuzala olishi, ya'ni bu
jarayonlar qaysi tomonga qarab borayotganligini, qanday sur'atlarda
borayotganligini his qilishi lozimBu jarayonlarni tadqiq qilish esa
matematikasiz mumkin emas. Bunda malamalik lalTakkurning, malamalik maniiqning,
matematik indüksiya, dedüksiya va silil kabilarning o'rni bcqiyos,
Bu o'rinda Abu Ali ibn Sino bulun
dunyo tan Olgan daho tabib bo'lishi bilan birga matematikani falsafiy
asoslarini, matematikani juda yaxshi bilganliklarini la'kidlab o'tmoqchimiz.
İbn Sino matematika sohasida ko'plab İzlanishlar olib borgan, Ular
qatoriga Evklidning "Negizlar" ( 13 kitobdan iborat) aşarini
qayta ishlab, unga Sharh va to'ldirishlar kiritganligini fa,xr bilan tilga
olamiz, Buyruk daho geometrik o'lchamlarga arifmetik
terminologiyalarni qo'llagan. Shuningdek alloma "son" tushunchasi
doirasini "natural son" dan ancha kcngaytirdi. "Aqsom al-ulum ![]() ilimlar
tasnifi") asarida nazariy ilmlar haqiqatni bilishga, amaliy ilmiar yaxshi
ishlarni bajarishga qaralilganligini e'tirof etik), bu asarda ham matematika
(geometriya, arifmctika; astronomiya, musiqa ) ning ahamiyati haqida juda
yaxshi
ilimlar
tasnifi") asarida nazariy ilmlar haqiqatni bilishga, amaliy ilmiar yaxshi
ishlarni bajarishga qaralilganligini e'tirof etik), bu asarda ham matematika
(geometriya, arifmctika; astronomiya, musiqa ) ning ahamiyati haqida juda
yaxshi ![]() fikrlarini bayon etgan. Yevropada va butun
dunyoda bir necha asrlar davomida bizning buyuk vatandoshimizning tibbiyotga
oid kitoblari darslik bo'lib kelganligi hech kimga sir emas. Shuningdek olimning
falsafaga oid eng yirik va muhim asari ”Kitob ash-shifo” ning uchinehi qismi
matematikaga bag'ishlanganligi bejis emas,
fikrlarini bayon etgan. Yevropada va butun
dunyoda bir necha asrlar davomida bizning buyuk vatandoshimizning tibbiyotga
oid kitoblari darslik bo'lib kelganligi hech kimga sir emas. Shuningdek olimning
falsafaga oid eng yirik va muhim asari ”Kitob ash-shifo” ning uchinehi qismi
matematikaga bag'ishlanganligi bejis emas,
Bu darslikdan foydalanuvchi talabalarga ham bo'lg'usi shifokorlik faoliyatlarida alloma Abu Ali ibn Sinodan taqlid qilishlarini, osz kasbiy faoliyatlarida matematik bilimlardan foydalanishlarini tilab qolamiz,
Matematika va matematik modellashtirish tibbiyot fanlardagi turli nazariy va amaliy masalalarni yechishda muvaffaqiyat bilan qo'llanib
![]() Matematik modellashtirish usłubi
masalani xarakterlaydigan u yoki bu kattalikni miqdor jihatdan ifodalash,
so•ngra bog'liqdigini o'rganish imkoniyatini beradi. Usłub asosida
matematik model tushunchasi yotadi,
Matematik modellashtirish usłubi
masalani xarakterlaydigan u yoki bu kattalikni miqdor jihatdan ifodalash,
so•ngra bog'liqdigini o'rganish imkoniyatini beradi. Usłub asosida
matematik model tushunchasi yotadi,
Matematik model deb o'rganilayotgan obyektni matematik formuła yoki algoritm ko•rinishida ifodalangan xarakteristikalari orasidagi funksional bog'lanishga aytiladi.
Komp'yuter ixtiro etilganidan so'ng matematik modellashning ahamiyati keskin oshdi. Murakkab tibbiy tizimlarni yaratish, so sngra ulami Komp'yuterlar yordamida tatbiq etishning haqiqiy imkoniyatlari paydo bo'ldi, Endilikda ob'ekt, yłť ni haqiqiy tizim ustida emas, balki uni almashtiruvchi matematik model ustida tajriba o'tkazila boshlandi,
Qon aylanish tizimi, murakkab nery,
limfa tugunlari, yurak va boshqalar bilan bog'liq bo'lgan ulkan
hisoblashlarning Komp'yuterda bajarilishi matematik modellash usłubining
samaradorligini tasdiqlaydi.![]()
Odatda, matematik model ustida hisoblash tajribasini o'tkazish
haqiqiy obyektni Iajribada tadqiq etish mumkin bo'lmagan yoki iqtisodiy
jixaldan ![]() maqsadga muvofiq bo'lmagan hollarda
o'tkaziladi, Bunday hisoblash tajribasining natijalari haqiqiy obyekt ustida
olib boriladigan tajribaga qaraganda juda aniq emasligini ham hisobga olish
kerak. Lekin shunday misollarni kellirish mumkinki* Komp'yuterda o'lkazilgan
hisoblash tajribasi o'rganilayotgan jarayon yoki hodisa haqidagi ishonchli
axborotning yagona manbai bo'lib xizmat qiladi. Masalan, faqat
maqsadga muvofiq bo'lmagan hollarda
o'tkaziladi, Bunday hisoblash tajribasining natijalari haqiqiy obyekt ustida
olib boriladigan tajribaga qaraganda juda aniq emasligini ham hisobga olish
kerak. Lekin shunday misollarni kellirish mumkinki* Komp'yuterda o'lkazilgan
hisoblash tajribasi o'rganilayotgan jarayon yoki hodisa haqidagi ishonchli
axborotning yagona manbai bo'lib xizmat qiladi. Masalan, faqat ![]() matematik
modellashtirish va Komp'yuterda hisoblash tajribasini o'tkazish yo'li bilan
korona virusning tarqalishi , uning insonga la' şiri oqibatlarini oldindan
aytib berisil mumkin, Komp'yutcr ko'rinmas virusli qurolsiz urushda mutloq
g'olib bo'lmasligini ko'rsatadi. Kompyuterli tajriba yer yuzida bunday urush
oqibatida ekologik ogzgarishlar, ya' ni haroralning keskin
o'zgarishi, atmosferaning changlanishi, qutblardagi muzliklarning crishi ro'y
berishi, xatto yer o'z o'qidan chiqib ketishi mumkinligini ko'rsatadi
matematik
modellashtirish va Komp'yuterda hisoblash tajribasini o'tkazish yo'li bilan
korona virusning tarqalishi , uning insonga la' şiri oqibatlarini oldindan
aytib berisil mumkin, Komp'yutcr ko'rinmas virusli qurolsiz urushda mutloq
g'olib bo'lmasligini ko'rsatadi. Kompyuterli tajriba yer yuzida bunday urush
oqibatida ekologik ogzgarishlar, ya' ni haroralning keskin
o'zgarishi, atmosferaning changlanishi, qutblardagi muzliklarning crishi ro'y
berishi, xatto yer o'z o'qidan chiqib ketishi mumkinligini ko'rsatadi![]()
Matematik modellashda berilgan inson
organizmidagi fizik jarayonlarning matematik ifodalari modellashtiriladi.
Matematik model ![]() tashqi dunyoning matematik belgilar bilan
ifodalangan qandaydir
tashqi dunyoning matematik belgilar bilan
ifodalangan qandaydir ![]() hodisalari sinfining taqribiy tavsifidir.
Matematik model tashqi dunyoni
hodisalari sinfining taqribiy tavsifidir.
Matematik model tashqi dunyoni ![]() jumladan insonni bilişil,
shuningdek, oldindan aytib berisil va boshqarishning kuchli uslubi hisoblanadi.
Matematik modelni tahlil qilish
jumladan insonni bilişil,
shuningdek, oldindan aytib berisil va boshqarishning kuchli uslubi hisoblanadi.
Matematik modelni tahlil qilish ![]() o'rganilayotgan hodisaning mohiyatiga
singish imkoniyatini beradi, Hodisalarni matematik model yordamida o'rganish
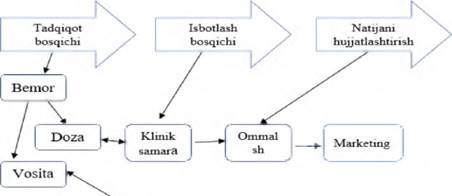
to'rt bosqichda amalga oshiriladi:
o'rganilayotgan hodisaning mohiyatiga
singish imkoniyatini beradi, Hodisalarni matematik model yordamida o'rganish
to'rt bosqichda amalga oshiriladi:
Birinchi bosqich - modelning asosiy ob'ekllarini bog'lovchi qonunlarni ifodalash,
Ikkinchi bosqich - modeldagi matematik masalalarni tekshirish.
Uchinchi hosqich - modelning qabul qilingan amaliyot mezonlarini qanoatlantirishini aniqlash Boshqacha aytganda, modeldan olingan nazariy natijalar bilan olingan ob'ektni kuzatish natijalari mos kelishi masalasini aniqlash.
To "rtinchi bosqich - o'rganilayotgan hodisa haqidagi ma'lumotlarni jamlash orqali modelning navbatdagi tahlilini o'tkazish va uni rivojlantirisll, aniqlashtirish. Shunday qilib, modellashtirishning asosiy mazmunini ob'ektni dastlabki o'rganish asosida modelni tajriba orqali va (yoki) namriy tahlil qilish, natijalarni 0b 'ekt haqidagi ma' lumotlar bilan taqqoslash, modelni tuzatish
(takomillashtirish) va shu kabilar tashkil etadi. Matematik![]()
 bosqlchi
bosqlchi
|
Tadqiq |
|
Model |
|
|
Muhim
|
|
 MODELLASHTIRISH
MODELLASHTIRISH
I-rasm, Modellashtirish sxemasi.
model tuzish uchun, dastlab masala rasmiylashtiriladi. Masala mazmuniga mos holda zarur belgilar kiritiladi. So'ngra kattaliklar orasida formuła yoki algoritm ko•rinishida yozilgan funksional bog'lanish hosil qilinadi, Aytib o'tilganlarni aniq sxemada ko'rib chiqamiz,
1.2-Š. Matematik induksiya va deduksiya
Induksiya yordamida diagnostika. Tibbiy tafakkurning barcha turlariga kasallik belgilaridagi o'xshashlik va farqlarni aniqlash uchun induktiv qobiliyatga ega bo'lishni taqozo etadi. Alomatning ta'rifi kasallikning mavjudligini va uning sababini ko'rsatmaydi,
I -Tashxisni to'g'ri tuzish va shakllantirish bu xulosalar, mulohazalar va tushunchalarning murakkab jarayoni.
2. Tibbiy hisobotlarning muvaffaqiyati, to'g•riligi va ishonchliligi xulosalar isbotlanganda, ular chuqur o'ylangan, tahlil qilingan va amalga oshirilganda paydo bo'ladi.
Induksiya tushunchasiga o stishdan avval o•xshatish tushunchasini tahlil etamiz. (Yxshatish belgisi qadimgi yunonlarda boshlanishida sonlar proporsiyasi shaklida ifodalangan, Masalan, 50 : 5 —70 : 7, Keyinchalik o'xshatish so'zi shakllarga va boshqa narsalarga ham tatbiq etila boshlandi.
Hozirgi paytda o'xshatish barcha fanlarda xizmat qiladi. Kimyo, biologiya fizika va geologiya fanlarida o'xshatishdan keng foydalaniladi„
Matematikada shunday masalalar mavjudki, ba'zi farazlar yakuniy natijalarga ko'ra, noto'g'ri bo'lib chiqadi. Shunday masalalardan biri
1640 yilda tug'ilgan P.Fermaning o'ziga tegishli hisoblanadi:
![]()
ko'rinishidagi natural sonlarning barchasi tub son deb faraz qilgan va faqat
lar uchun tekshirgan. Lekin 1732 yili Leonard Eyler Pyer Fermaning farazini inkor etdi, Uning xatoligi shunda ediki,
![]()
bir nechta xususiy qiymatlar uchun hisoblab (bu xususiy tasdiq),
![]()
ning qiymati ixtiyoriy n natural son uchun tub son degan umumiy xulosaga kelgan. L.Eyler sodda induksiya xatolikka olib kelishi haqidagi haqiqatni aytgan,
Matematikada cheksiz to'plam haqida mulolwa bildirilganda, chekli to'plamni tekshirish isbotlashni almashtira olmaydi,
Shunday qilib, ikkita tushunchani farqlash lozinv
l) Xususiy tasdiq;2)Umimiy tasdiq.
Umumiy tasdiqdan xususiy tasdiqga o'tish deduksiya deyiladi.
Masalan, quyidagi tasdiqlardan qaysi bir xususiy, qaysi biri umumiy:
l) O raqami bilan tugallanuvchi son 5 ga qoldiqsiz bo'linadi;
2) 60 soni 5 ga qoldiqsiz bo'linadi,
Xususiy tasdiqdan umumiy tasdiqga o'tish induksiya deyiladi.
Induksiya ham to'g'ri, ba'zida noto'g'ri natijaga olib kelishi murnkin. Induksiya metodi matematikada keng qo'llaniladi, lekin undan to'g'ri foydalanish lozim.
Xulosa:
I) Barcha nol raqami bilan tugallanuvchi sonlar 5 ga qoldiqsiz bo'linadi ( to'g'ri )
2) Barcha uch xonali sonlar 5 ga qoldiqsiz bo'linadi (noto'g'ri).
Bu usul hozirgi kunda matematik induksiya metodi deyiladi. Ushbu metoddan ba'zi qadimgi grek olimlari ham foydalanishgan, Dastalab bu metod 1321 yilda Gersonid tomonidan foydalanilgan. XIX asrning ikkinchi yarmigacha bu metod asosiy isbotlash metodi hisoblangan. Maiemalik induksiya — matematik induksiya prinsipiga asoslangan matematik tasdiqni isbotlovchi metod:
Agar A tasdiq n=l da o'rinli
ekanligi isbotlangan bo'lsa, x natural parametrga bo'g'liq va ixtiyoriy n
natural son uchun A (n) to'g'ri deb faraz qilinsa va n+l uchun.'Í (11+1)
to'g'riligi isbotlanadi va A(n) tasdiq ![]() illtiyoriy n da isbotlangan deb
hisoblanadi tasdiqning isbotlani shi induksiyaning birinchi qadarni
hisoblanadi, A(n) uchun to•g'ri degan farazdan A(n+l) ning isbotlanishi
induksiyali o'tish deyiladi. Bunda n induksiya parametri deyiladi, A (n+l) ni
isbotlashda A(n) ni faraz qilish
illtiyoriy n da isbotlangan deb
hisoblanadi tasdiqning isbotlani shi induksiyaning birinchi qadarni
hisoblanadi, A(n) uchun to•g'ri degan farazdan A(n+l) ning isbotlanishi
induksiyali o'tish deyiladi. Bunda n induksiya parametri deyiladi, A (n+l) ni
isbotlashda A(n) ni faraz qilish ![]() induktivli faraz deyiladi.
induktivli faraz deyiladi.
Matematik induksiya metodining mohiyati quyidagicha:
Agar tasdiqlash ketma-ketligi
mavjud bo'lsa, birinchi tasdiq to'g'ri ![]() va har bir to'g'ri tasdiqan so'ng to'g'ri
tasdiq mayiud bo'lsa, ketmaketlikdagi barcha tasdiqlar to'g'ri hisoblanadi.
va har bir to'g'ri tasdiqan so'ng to'g'ri
tasdiq mayiud bo'lsa, ketmaketlikdagi barcha tasdiqlar to'g'ri hisoblanadi.
Shunday qilib, matematik induksiya metodi yordamida isbotlash ikkita teoremadan iborac
1-teorema. n uchun tasdiq to'g'ri![]()
2-teorema. lxtiyoriy uchun tasdiq to'g'ri deb faraz qilinsa va navbatdagi nyk+l natural son uchun tasdiq to'g•riligi isbotlanadi.
Agar ikkala ushbu teoremalar
isbotlangan bo'lsa, matematik ![]() induksiya tamoyiliga asoslangan holda,
tasdiq ixtiyoriy n natural son uchun to'g'ri deb xulosa qilinadi.
induksiya tamoyiliga asoslangan holda,
tasdiq ixtiyoriy n natural son uchun to'g'ri deb xulosa qilinadi.
Matematik induksiya metodi yordamida quyidagi ayniyatlar isbotlang.
I-masala
![]() 2 (1)
2 (1)
ni isbotlang.
Yechish:
Sn=l+ ![]() belgilash kiritamiz. l)
n—lda Si—lga ega bo'lamiz. ni (l) tenglikning o'ng tomoniga qo'yamiz:
belgilash kiritamiz. l)
n—lda Si—lga ega bo'lamiz. ni (l) tenglikning o'ng tomoniga qo'yamiz:
![]()
2 n=l da (l) tenlikning o'ng va chap tomoni I ga teng ekanligini hosil qildik.
![]()
2
(l) tenglik n=k+l uchun o'rinli ekanligini isbotlash lozim:
![]()
2
Haqiqatdan ham: Sk_ 1 +2 + + k
Sk+l = 1 + 2 + + k + (k + 1)![]()
2
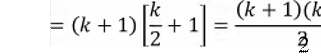
Tenglik isbotlandi.
2-masala. Tengl ikni ixtiyoriy n natural son uchun to'g'riligini isbotlang
![]()
A K, Yusupova, AYA„Abdumanonov
GRAFLAR NAZARIYASI
Texnik muharrir: R.Axmedov![]()
Badiiy muharrir: DTursunaliyeva
Sahifalovchi: S. Rahimova
Bosishga ruxsat etildi: 2022 Nashriyot bosma tabog'i: 18,75, Shanli bosma tabog'i: 9,375, Bichimi: 84x108 1/16.Adadi: 100 "Poligraf Super Servis” MCHJ
Manzil: 150100, Farg'ona viloyati, Farg'ona shahri„ Aviasozlar ko'chasi„ 2-uy
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.