МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОРЕНБУРГСКОЙ ОБЛАСТИ

Государственное автономное профессиональное образовательное

учреждение «Бузулукский строительный колледж»

г.Бузулука Оренбургской области

 

 

РАССМОТРЕНО И ОДОБРЕНО  на заседании ПЦК               Протокол №___  от «___»______20__г Руководитель ПЦК __________/_Е.Ю. Корочкина

УТВЕРЖДАЮ                        Зам. директора по УР                                  ________Е.Н. Индерейкина                                «___» ________     20__   г.

 

 

 

 

 

 

 

 

 

 

КОМПЛЕКТ

КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ 

 

по дисциплине ЕН. 01 «Математика»

 

 специальности 21.02.01 « Разработка и эксплуатация нефтяных и газовых месторождений»

 

 

 

 

 

 

Разработчик: преподаватель

 Болдырева Марина Анатольевна

 

 

 

 

 

 

 

Бузулук, 2019

 1. Общие положения

 

Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины Математика.

КОС включают контрольные материалы для проведения текущего контроля и промежуточной аттестации в форме экзамена.

КОС разработаны в соответствии с:

программой подготовки специалистов среднего звена по специальности  21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений;

программой учебной дисциплины Математика.

 

2. Результаты освоения дисциплины, подлежащие проверке

 

Результаты обучения[1] (освоенные умения, усвоенные знания)	Код контролируемой компетенции или ее части	Основные показатели оценки результатов
У1 решать прикладные задачи в профессиональной деятельности;	ОК 1-5, ОК-7-9    ПК 1.1  ПК 1.2  ПК 1.3  ПК 1.4  ПК 2.1  ПК 2.5  ПК 3.1  ПК 3.3	-дает определение основным математическим  понятиям (методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятности и математической статистики), выявляет взаимосвязи между ними; -применяет  терминологию и знания по общим вопросам  теории математики  для решения конкретных  практических задач
З 1 значение математики в профессиональной деятельности и при освоении ППССЗ;	ОК 1-5, ОК-7-9 ПК 1.1  ПК 1.2  ПК 1.3  ПК 1.4  ПК 2.1  ПК 2.5  ПК 3.1  ПК 3.3	-называет и анализирует  содержание и назначение математики; -определяет значение математики в профессиональной деятельности; -выделяет ключевые темы при освоении ППССЗ
З 2 основные математические методы решения прикладных задач в области профессиональной деятельности;	ОК 1-5,   ОК-7-9  ПК 1.1  ПК 1.2  ПК 1.3  ПК 1.4  ПК 2.1  ПК 2.5  ПК 3.1  ПК 3.3	-перечисляет основные математические методы, дает им характеристику; -называет алгоритм решения каждого метода; -перечисляет и характеризует основные методы решения прикладных задач в области профессиональной деятельности
З 3  основные понятия и методы математического анализа	ОК 1-5,   ОК-7-9   ПК-1.1   ПК-1.2   ПК3.1	-формулирует понятие функции, перечисляет способы задания, строит графики элементарных функций; - дает определение предела функции и вычисляет предел; -знает определение, таблицу и правило вычисления производных, геометрических и механических смысл; -знает как использовать приложение производной к исследованию функции; -называют основные формулы интегрирования; - знает как использовать приложение определенного интеграла к вычислению различных величин; -знает алгоритм решения прикладных задач на составление дифференциального уравнения.
З 4  основные понятия и методы линейной алгебры	ОК 1-5,   ОК-7-9   ПК-2.1	-дает определение матрицы, знает правила элементарных операций над ними; -владеет алгоритмом вычисления определителей первого, второго и третьего  порядков; -знает алгоритм решения систем линейных уравнений;
З 5  основные понятия и методы теории комплексных чисел;	ОК 1-5,   ОК-7-9   ПК-1.3	-дает определение множества рациональных чисел; -имеет понятие о мнимых и комплексных числах; -имеет представление о записи комплексного числа в различных формах; -знает правило выполнения действий над комплексными  числами, записанных  в различных формах.
З 6  основные понятия и методы  теории вероятности и математической статистики;	ОК 1-5,   ОК-7-9   ПК-1.1   ПК-1.2   ПК2.1   ПК2.5   ПК3.1   ПК3.3	-дает классическое  определение вероятности; -формулирует основные теоремы сложения и умножения вероятностей; -формулирует закон распределения случайной величины; -знает основные понятия математической статистики, группирует статистические данные.
З.7 основы интегрального и дифференциального исчисления.	ОК 1-5,  ОК-7-9  ПК 1.1  ПК 1.2  ПК 2.1	- освоил знания вычисления  интегралов по формулам прямоугольников, трапеций и формуле Симпсона и оценке погрешностей, умений вычислять интегралы численными методами; - перечисляет и характеризует формулы приближенного дифференцирования.

 

 

 

3. Распределение оценивания результатов обучения по видам контроля

 

 

 

4. Структура контрольных заданий

4.1. Задания текущего контроля

 

Наименование раздела: 1. Элементы математического анализа

 

Перечень объектов контроля и оценки

 

 

Тексты заданий

 

№1 Тест 1 Тест по теме1.1  Основы дифференциального исчисления.

 

Вариант 1

1.      Производная функции y = 5x² – 7x +1 равна

А) 10x – 7 +1       B) 10x – 7        C) 3x

2.      Производная функция y = 10x⁷ (x – 2) равна

А) 70x⁶                  B) 80x⁷              C) 80x⁷ – 140x

3.      Точка х₀ называется стационарной, если производная в точке х₀

А) больше 0        В) меньше 0     С) равна 0

4.      Если производная функции  меньше 0 на некотором промежутке, то функция на этом промежутке

А) возрастает      В) убывает       С) постоянна

5.      Функция  принимает  свое  наименьшее  значение

А) в точке минимума или на конце промежутка

В) в точке минимума

С) на конце промежутка

6.        Производная от скорости по времени равна

А) ускорению     В) скорости      С) производному  пути

7.        Производная функция  y = 3^4x равна

А) 4∙3^4x                       В) 4ln 3∙3^4x       C) 12∙3^4x

8.                  Угловой коэффициент касательной к графику функции y = 5x² – 1   в точке  х₀ = 1 равен

А) 9                     В) 5                     С) 10

9.   Функция F(x), производная которой равна f(x), называется…

А) первообразной для f(x);

В) интегралом от f(x);

С) производной от f(x).

10.   Функция F(x), производная которой равна f(x), называется…

А) первообразной для f(x);

В) интегралом от f(x);

С) производной от f(x).

2 вариант

1. Производная функция y = sin 8x +5 равна

А) 8 cos 8x           B) cos 8x+5      C) 8 sin 8x +5

2.Функция возрастает на некотором промежутке, если ее производная

А) больше 0        В) меньше 0     С) равна 0

3Если при переходе через точку х₀ производная меняет знак с «+» на  «- », то эта точка будет точкой

А) минимума        В) наибольшего значения       С) максимума

3.Производная функции в точке х₀  равна

А) наименьшему значению функции в точке х₀

В) угловому коэффициенту касательной к данной функции в точке х_0.

С) наибольшему значению функции в точке х_0.

4.  Производная от пути по времени равна

А) ускорению     В) скорости      С) производному  пути

5.  Производная функция y =  равна

А) 2                 В) 2+5          С) +5

6.  Производная  от  заряда  есть

А) сила тока       В) напряжение      С) сопротивление

7.   Про производную функции f(x) можно сказать, что это…

А) предел отношения приращения функции к приращению аргумента;

В) главная, линейная часть приращения y функции;

С) совокупность первообразных функций F(x)+С.

8.   Про производную функции f(x) можно сказать, что это…

А) предел отношения приращения функции к приращению аргумента;

В) главная, линейная часть приращения y функции;

С) совокупность первообразных функций F(x)+С.

9.   Для функции y = f(x) величина, вычисляемая по формуле f (x+) – f(x),  называется …

А) дифференциалом функции dy;

В) приращением функции y;

С) производной f^/(x).

   10.   Значение  производной функции в точке x₀…

     А) показывает ускорение изменение функции;

     В) всегда равна 0;

     С) показывает  скорость изменения функции.

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	9-10
«Хорошо»	7-8
«Удовлетворительно»	5-6
«Неудовлетворительно»	Менее 5

 

№ Верно ли выполнено задание:

Пример 1. Вычислить пределы функций 

Решение.

     Используя теоремы о пределах и формулы  (2)-(5) получим  /да/

Пример 2. Вычислить пределы функций 

Решение.

       Для того, чтобы вычислить предел функции в точке подставим значение аргумента функции в этой точке, т.е. вместо х подставим единицу:  /да/

 

Пример 3. Вычислить пределы функций 

Решение.

      Имеем неопределённость вида. Используя  правило раскрытия неопределённостей (а) воспользуемся формулами сокращённого умножения: .    /да/

 

Пример 4. Вычислить пределы функций    

Решение.

        Имеем неопределённость вида. Используя  правило раскрытия неопределённостей, разделим каждое слагаемое почленно на :      /да/

 

Пример 5 Вычислить пределы функций 

Решение.

      Неопределённость вида. Решим уравнения числителя и знаменателя и разложим трёхчлены на множители: = 

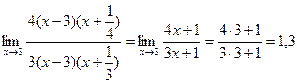
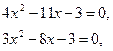
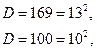
             /нет/

 

Пример 6.  Вычислить пределы функций   

Решение

     Неопределённость вида. Домножим и числитель, и знаменатель на сопряжённый множитель: /да/

 

Пример 7  Вычислить пределы функций 

Решение

      Имеем неопределённость вида. Произведём деление многочленов столбиков на (х-2):

 =

       x³ - 5x² + 8x – 4    x –2                                             x³ – 3x² + 4      x – 2

       x³ – 2x²               x² – 3x +3(2)                                    x³ – 2x²         x² – x –4 (2)

      -3x² +8x                      ошибка                                        - x² + 4              ошибка

      -3x² +6x                                                                          - x² + 2x

                2x – 4                                                                       -2x +4

                2x – 4                                                                       -2x +4

                        0                                                                                0

    Пример 8.  Вычислить пределы функций   

Решение.

      Имеем неопределённость вида. Применим первый замечательный предел,

формулы (9), (10) получим: 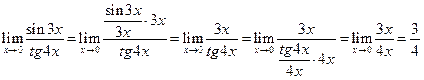 /да/

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	нашли 3 ошибки
«Хорошо»	нашли 2 ошибки
«Удовлетворительно»	нашли 1 ошибку
«Неудовлетворительно»	не нашли ошибок

  №2  Письменный опрос

Вариант.

1.Найти производные элементарных функций

 

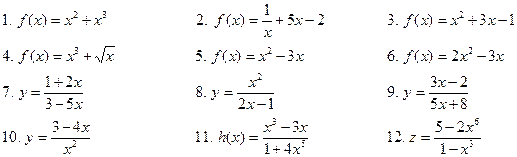
Вариант 2.

Найти производные элементарных функций

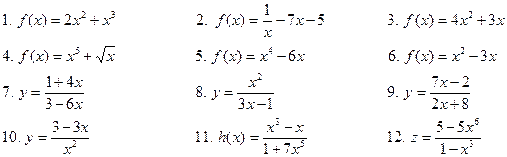
Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	11-12
«Хорошо»	9-10
«Удовлетворительно»	6-8
«Неудовлетворительно»	Менее 6

 

№3  Письменный опрос

Вариант 1.

1.Исследовать функцию на экстремум, найти точки перегиба, асимптоты и построить график

             функции y = f(x), если:

                        а)                                б)

2.Зависимость пути от времени при прямолинейном движении задана уравнением S = S(t).

             Найти максимальную скорость движения тела и момент времени, когда она будет

             достигнута, если:

  (м)

Вариант 2.

 

1.Зависимость пути от времени при  прямолинейном движении задана уравнением S = S(t).   

   Найти максимальную скорость движения тела и момент времени, когда она будет 

             достигнута, если:

  (м)

2. Найти наибольшее и наименьшее значения функции y = f(x) на отрезке , если:

                                       

 

Критерии оценки

 

Оценка	Количество правильных примеров
«Отлично»	3
«Хорошо»	2
«Удовлетворительно»	1
«Неудовлетворительно»	Менее 1

 

 

Тест по теме1.2  Основы интегрального исчисления.

1 вариант      

1.  Среди заданных функций определить ту, производная которой  равна 9x²

     А) y = x³ + 1                 B) y = 3x³ – 1                C) y = x²

2.    Заряд – это интеграл     от…

А) силы                       В) силы тока                 С) плотности

3.    Для какой  функции F(x) = 1 + sin x  является первообразной

А)  x + sin x                  B) x + cos x                    C) cos x   

4.   Какому свойству удовлетворяет функция y(x), если  её  производная   равна нулю…

А) возрастает             В) постоянна                   С) убывает.

5.   Назвать верную пару «функция – график производной этой функции»

А)  y = 2 и парабола   В) y = 2x и ось ОХ    С) y = x² и возрастающая

                                                                                                          прямая.

6.   Если функция  при переходе через точку меняет свой знак с «-» на «+», то это точка…

А)  минимума             В) максимума                   С) возрастания

 

7.   Найти первообразную  функции 2x +1

A)  x(x +1) + C            B)  x² + 1 + C                      C)  x² - 2x + C.

 

8.   Для какой функции  5sin 3x – 7 будет первообразной?

А)  15cos 3x                B)  5cos 3x – 7x                   C)  -5cos 3x

9.   Какой закон движения у свободно падающего со скоростью V = gt  тела?

А) S = g                       B)  S =                        C)  S = 2gt

10.   Вычислите

А)  х                             В)  в – а                                   С) 0

 

2 вариант

  1. Путь – это интеграл          от…

      А) силы                       В) скорости                   С) ускорения

2.     Масса – это интеграл    от…

А) скорости                В) силы                          С) плотности.

3.    Функция F(x) является первообразной для f(x), если …

  А) f^′′  (x) = F(x)            B)  F(x) = f(x)                  C)  F^/ (x) = f(x).

 

4.   Скорость – это производная от…

А)  ускорения             В) пути                             С) силы.

5.   Какое из следующих свойств имеется у производной функции,  если оно  есть у  функции?

А)  четность                В) монотонность             С) периодичность.    

^{6.   Найти первообразную  функции 2x +1}

A)  x(x +1) + C            B)  x² + 1 + C                      C)  x² - 2x + C.

7.   Найти функцию, производная которой y^/ =

A)                   B)                          C) cos x

8.   Найти уравнение кривой, если угловой коэффициент касательной   равен к = 2х

А) y = 2                      B) y = 2x² +C                           C) y = x² +C.

9.   Найти первообразную  функции 2x² +х

A)  2/3x²(x +1) + C            B) 2/3 x³ + x² + C                      C)  2/3x³ - 2 x²+ C

10.   Чему равен определенный интеграл

А)  F(b) – F(a)             B) f(x)                                    C)  F(x) + C

 

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	9-10
«Хорошо»	7-8
«Удовлетворительно»	5-6
«Неудовлетворительно»	Менее 5

 

№2.Письменный опрос

Вариант 1

Найти неопределенный интеграл:

1)

2)

3)

4)                      5)

5) Вычислить определенный интеграл:

а) 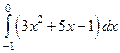;            б)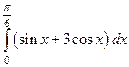

6) Скорость движения тела задана уравнением  (м/с). Найти путь, пройденный телом за вторую секунду движения.

Вариант 2

Найти неопределенный интеграл:

1)

2)

3)

4)                      5)

5) Вычислить определенный интеграл:

а) 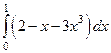;               б)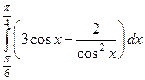

6) Найти путь, пройденный телом от начала движения до остановки, если его скорость задана уравнением ((м/с).

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	8
«Хорошо»	7
«Удовлетворительно»	5-6
«Неудовлетворительно»	Менее 5

 

 

Тема 1.3  Дифференциальное уравнение .

№1 математический диктант

1. Дайте определение дифференциального уравнения первого порядка.

2. Что называется порядком   дифференциального уравнения?                                    

3. Что называется решением   дифференциального уравнения?       

4. Как называется условие y(x₀)=y₀ ?

5. Какое дифференциальное уравнение называется обыкновенным?

6. Верно ли составлен алгоритм решения прикладных задач на составление дифференциального уравнения?

Алгоритм решения прикладных задач:

1.Из переменных величин выделить функцию и аргумент, установить физический смысл функции, производной от неё.

2. На основании известных сведений из физики, механики, электротехники и других дисциплин установить зависимость между функцией, её производной и аргументом т.е. составить дифференциальное уравнение.

3.Определить, к какому типу относится составленное дифференциальное уравнение.

4.Решить дифференциальное уравнение, найти его общее решение.

5.Если в задаче даны начальные условия, получить частное решение.

6. Какое дифференциальное уравнение называется обыкновенным?

 

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	6 (но в 6 задании есть 2 недочета)
«Хорошо»	5 (если верно выполнено 6 задание)
«Удовлетворительно»	4
«Неудовлетворительно»	Менее 4

 

 

Наименование раздела: 2.Основные понятия линейной алгебры

 

Перечень объектов контроля и оценки

                                  

  Тексты заданий

 

Задание по теме 2.1 Матрицы. Операции над матрицами.

№1 Математический диктант

1. Равны ли матрицы?

а) А = , В = (2 0)

б) Составьте матрицы А и В, чтобы А = В и А  В

2. Найти сумму матриц

 

 

а) А = ,  В =

б) Составьте 2 матрицы одинаковых (4х4) размеров и найдите их сумму.

3. Найдите произведение матриц.

 

а) А =  на число 2

б) придумайте матрицу (2х3) и умножьте на  - 2.

 

4. Даны матрицы  А = , В =

а) Найти разность: В – А  и  А - В

 

б) Найдите 2А – 3В

 

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	7-8
«Хорошо»	5-6
«Удовлетворительно»	4
«Неудовлетворительно»	Менее 4

 

 

Задание по теме 2.2Определители.

 

Письменный  опрос

1 вариант

1.Вычислить определители:

 

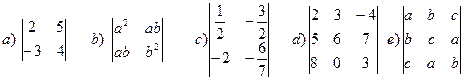
2 вариант

1.Вычислить определители:

 

 

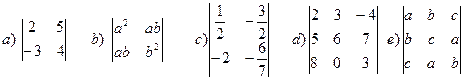
Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	5
«Хорошо»	4
«Удовлетворительно»	3
«Неудовлетворительно»	Менее 3

 

Задание по теме 2.3 Методы решения систем линейных уравнений.

 

Письменный  опрос

1вариант-четные задания, 2 вариант -  нечетные.

Решите систему уравнений:

                            

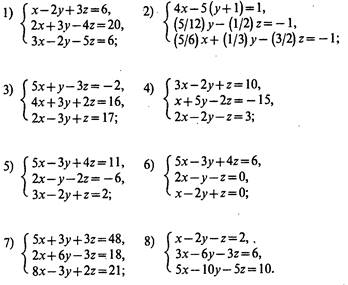
Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	4
«Хорошо»	3
«Удовлетворительно»	2
«Неудовлетворительно»	Менее 2

 

 

 

Наименование раздела: 3. Основные понятия теории комплексных чисел.

 

Перечень объектов контроля и оценки

                                 

                                                 Тексты заданий

 

Задание по теме 3.1 Понятие комплексного числа.

 

Письменный опрос. Математический диктант.

Запишите:

1. Определение комплексного числа.

2.Запишите  комплексное число в алгебраической  форме.

3.Дайте определение модуль и аргумента  комплексного числа.

4.  Приведите примеры

 5.Какие действия над комплексными числами в алгебраической форме вы умеете выполнять?

 6.Запишите правила.

  7. 1 вар. Выполнить действия в алгебраической форме записи:

а)      б)     в)

  7. 2вар. Выполнить действия в алгебраической форме записи:

а) ;        б) ;        в)

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	9
«Хорошо»	7-8
«Удовлетворительно»	6
«Неудовлетворительно»	Менее 6

 

Задание по теме 3.2 Формы комплексных чисел.

№1 Письменный опрос

Вариант 1

1)      Выполнить действия в алгебраической форме записи:

а) ;         б) ;       в)

2)      Записать комплексные числа в тригонометрической форме и выполнить действия:

а) ;        б) ;            в)

3)      Выполнить действия над комплексными числами в показательной форме:

а) ;        б) ;            в)

4)      Выполнить действия в показательной форме. Ответ записать в алгебраической форме

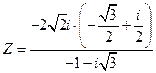
Вариант2

1)      Выполнить действия в алгебраической форме записи:

а) ;         б) ;       в)

2)      Записать комплексные числа в тригонометрической форме и выполнить действия:

а) ;        б) ;            в)

3)      Выполнить действия над комплексными числами в показательной форме:

а) ;        б) ;            в)

4)      Выполнить действия в показательной форме. Ответ записать в алгебраической форме

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	13-14
«Хорошо»	11-12
«Удовлетворительно»	8-10
«Неудовлетворительно»	Менее8

 

№2 тест

 

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	10
«Хорошо»	8-9
«Удовлетворительно»	6-7
«Неудовлетворительно»	Менее6

 

 

Терминологический диктант по разделу «Формы комплексных чисел»

1 вариант – тригонометрическая форма комплексного числа, мнимая единица, вычитание и деление комплексных чисел (алгебраическая форма), модуль комплексного числа, аргумент комплексного числа, алгебраическая форма комплексного числа, формула Муавра, показательная форма комплексного числа, формула Эйлера.

2 вариант – алгебраическая  форма комплексного числа, действительные числа, сложение и умножение комплексных чисел (алгебраическая форма), геометрическая интерпретация комплексного числа, аргумент комплексного числа, тригонометрическая  форма комплексного числа, извлечение корня из комплексного числа, показательная форма комплексного числа, приложение комплексных чисел.

Критерии оценки

-    оценка «отлично» выставляется обучающемуся, если всем предложенным терминам дана правильная расшифровка;

-    оценка «хорошо»  - если один термин не расшифрован или к двум терминам дана не точная формулировка;

-    оценка «удовлетворительно»  - если допущена ошибка в формулировки двух-трех терминов, или на дана расшифровка двух терминов;

-    оценка «неудовлетворительно» - если половина терминов не расшифрованы или сделаны практически во всех формулировка ошибки.

 

 

Наименование раздела: 4. Основные понятия теории вероятностей и мататической статистики

 

Перечень объектов контроля и оценки

Тексты заданий

 

№1 Задание по теме 4.1 Элементы теории вероятностей.

Письменный опрос.

1.В бригаде 12 человек нужно выбрать бригадира, инженера, механика. Сколькими способами это можно сделать?

 

2.Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книги окажутся поставленными рядом (событие С).

 

3.Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу 5 билетов, один выигрышный.

 

4.Из колоды карт (52 карты) наудачу извлекают 3 карты. Найти вероятность того, что это тройка, семерка, туз.

 

5.Ребенок играет с пятью буквами разрезной азбуки А, К, Р, Ш, Ы. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «Крыша».

 

6.В ящике находятся 6 белых и 4 красных шара. Наудачу берут два шара. Какова вероятность того, что они окажутся одного цвета?

 

7.В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	7
«Хорошо»	6
«Удовлетворительно»	5
«Неудовлетворительно»	Менее 5

 

 

Задание по теме 4.2 Случайная величина и функция ее распределения.

№1 Письменный опрос.

1.Составить закон распределения числа попаданий в цель при шести выстрелах, если вероятность попадания при одном выстреле равна 0,4.

 

2.Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,3. Составить закон распределения числа библиотек, которые он посетит, если в городе четыре библиотеки.

 

3.Охотник стреляет по дичи до первого попадания, но успевает делать не более четырех выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

 

4.Найти математическое ожидание случайной величины X, если закон ее распределения задан таблицей:

 

Х	1	2	3	4
р	0,3	0,1	0,2	0,4

 

5.На заводе работают четыре автоматические линии. Вероятность того, что в течении рабочей смены первая линия не потребует регулировки, равна 0,9, вторая – 0,8, третья – 0,75, четвертая – 0,7. найти математическое ожидание числа линий, которые в течение рабочей смены не потребуют регулировки.

6.Найти дисперсию случайной величины Х, зная закон ее распределения:

 

Х	0	1	2	3	4
р	0,2	0,4	0,3	0,08	0,02

 

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	6
«Хорошо»	5
«Удовлетворительно»	4
«Неудовлетворительно»	Менее 4

 

№2 Тест

Задание 1.

Событием в теории вероятностей называется

A. Kомплекс условий, необходимых для проведения эксперимента.

B. Pезультат испытаний.

C. Запланированный эксперимент.

D. Комплекс условий, которые могут выполняться в эксперименте, но могут и не выполняться.

Задание 2.

Абсолютная частота случайного события – это

A. отношение числа опытов, благоприятствующих данному испытанию, к общему числу испытаний;

B. число опытов, благоприятствующих данному событию;

C. предел, к которому стремится относительная частота события при числе опытов, стремящихся к бесконечности;

D. отношение общего числа опытов к числу опытов, благоприятствующих данному испытанию;

E. общее число испытаний.

Задание 3.

Относительная частота события – это

A. число опытов, благоприятствующих испытанию;

B. отношение количества опытов, благоприятствующих испытанию, к общему числу испытаний;

C. отношение общего числа опытов к числу испытаний, которые благоприятствуют наступлению интересующего события

D. предел отношения общего числа испытаний к числу благоприятных событий.

Задание 4.

Случайным называется событие,

A. которое может произойти только при большом количестве опытов;

B. которое может произойти, но может и не произойти в результате данного опыта;

C. которое может произойти только в том случае, если произойдет событие, с ним связанное;

D. вероятность которого равна 1.

E. которое не входит в полную группу событий

Задание 5.

Достоверным называется событие,

A. которое входит в полную систему событий;

B. которое является противоположным случайному событию;

C. которое обязательно наступит в результате испытания.

D. вероятность которого меньше 1.

E. которое может произойти, но может и не произойти в результате испытаний.

Задание 6.

Какое значение вероятности соответствует достоверному событию?

A.. От 0,7 до 1;

B. 1;

C. От 0 до 1.

D. От 0,3 до 0,7.

E. От 0 до 0,3.

Задание 7.

Какое значение вероятности соответствует невозможному событию?

A. От -1 до 1.

B. От 0 до 0,3

C. Равное 0.

D. От 0 до 1.

E. От 0,7 до 1.

Задание 8.

Невозможным называется событие, которое

A. противоположно случайному.

B. не входит в полную группу событий.

C. никогда не может произойти в результате данного опыта.

D. никогда не может произойти, если произошло событие А.

E. никогда не происходит, если число испытаний невелико.

Задание 9.

Совместными называются события

A. которые наступают одновременно и образуют полную группу событий.

B. которые могут наступать одновременно в результате данного испытания.

C. которые образуют полную группу событий.

D. А и В, при этом событие А наступает, если произошло событие В.

E. которые равновероятны и образуют полную группу событий.

Задание 10.

Несовместные называются события,

A. которые имеют неодинаковые вероятности появления.

B. вероятность которых равна нулю.

C. которые никогда не могут наступать одновременно в результате данного опыта.

D. для которых вероятность события А не изменяется при появлении события В.

E. которые никогда не могут произойти.

Задание 11.

Зависимыми называются события А и В, если

A. Они имеют неодинаковые вероятности появления.

B. Вероятность наступления события В изменяется в зависимости от того, произошло ли событие А.

C. Они никогда не могут наступать одновременно в результате данного опыта.

D. Они могут наступать одновременно в результате данного испытания.

E. Они противоположны друг другу.

Задание 12.

Независимыми называются события А и В, если

A. они противоположны друг другу;

B. они никогда не могут наступать одновременно в результате данного опыта;

C. вероятность наступления события В не изменяется в зависимости от того, произошло ли событие А.

D. вероятность их одновременного наступления равна нулю.

E. событие А не наступает в том случае, когда первым произошло событие В.

Задание 13.

Чему равна сумма вероятностей противоположных событий?

A. 1

B. 0

C. 0,5

D. 0,7

E. 0,3

Задание 14.

Теорема полной вероятности применяется в тех случаях, когда необходимо рассчитать

A. вероятность гипотезы при условии, что событие уже произошло;

B. вероятность события, которое может произойти с одной из гипотез, образующих полную систему;

C. вероятность одной их гипотез, входящих в полную группу событий.

D. вероятность события при условии, что одна из гипотез уже реализовалась.

Задание 15.

Полную группу несовместных событий образуют события А₁, А₂,…,А_n

A. которые наступили в результате проведения испытаний.

B. которые являются совместными и равновозможными.

C. которые несовместны и в результате каждого испытания появляется только одно из этих событий.

D. вероятность которых одинакова.

E. которые являются зависимыми и достоверными.

Критерии оценки

Оценка	Количество правильных ответов
«Отлично»	14-15
«Хорошо»	12-13
«Удовлетворительно»	8-11
«Неудовлетворительно»	Менее 8

 

 

 

 

Наименование раздела: 5.Основы интегрального и дифференциального исчисления

 

Перечень объектов контроля и оценки

                                 

                                          Тексты заданий

 

Задание по теме 5.1 Численное интегрирование.

№1 Проверочная работа

1 вариант

1.Найдите приближенные значения степеней:

а) (9,06)² ; б) (9,95)³; в) (0,975)⁴.

2.Найдите приближенные значения корней:

а) ³√1,012;    б)√24,84;   в)√99,5; 

3.Вычислите:

А)sin=42^/;    б)tg1⁰12^/

   2 вариант

1.Найдите приближенные значения степеней:

а) (1,012)³;    б) (1,005)¹⁰;     в) (9,06)²

2.Найдите приближенные значения корней:

а) √25,16;    б)√101;   в)¹⁰√1,03; 

3.Вычислите:

А)sin=2⁰06^/;       б)tg3⁰18^/

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	8
«Хорошо»	6-7
«Удовлетворительно»	4-4
«Неудовлетворительно»	Менее 4

 

№2 Терминологический диктант по разделу «Основы интегрального и дифференциального исчисления»

1 вариант – интеграл, неопределенный интеграл, формула Ньютона – Лейбница, криволинейная трапеция, приближенное интегрирование, формулы прямоугольников, формула трапеций, формула Симпсона, погрешность приближения, относительная погрешность.

2 вариант - интеграл, определенный интеграл, пределы интегрирования, площадь криволинейной трапеции, пределы  интегрирования, формулы прямоугольников, формула трапеций, формула Симпсона, подынтегральная функция, абсолютная погрешность.

Критерии оценки

-    оценка «отлично» выставляется обучающемуся, если всем предложенным терминам дана правильная расшифровка;

-    оценка «хорошо»  - если один термин не расшифрован или к двум терминам дана не точная формулировка;

-    оценка «удовлетворительно»  - если допущена ошибка в формулировки двух-трех терминов, или на дана расшифровка двух терминов;

-    оценка «неудовлетворительно» - если половина терминов не расшифрованы или сделаны практически во всех формулировка ошибки.

 

№3Диагностический тест

1.     В виде какого числового ряда можно представить интеграл  

a)     ;

b)    ;

c)     

2.     Чему равен первый член разложения в ряд Маклорена подынтегральной

функции интеграла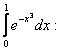 

a)     - 1;

b)      1;

c)       е.

3.    Какого вида получим квадратурные формулы, если заменить подынтегральную функцию каким-либо интерполяционным многочленом:

a)     ;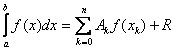

b)    ;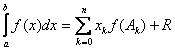

c)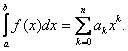      

4.     Какая из формул называется формулой Симпсона:

a)     ;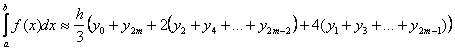

b)    ;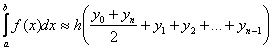

c)     .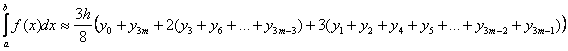

5.    Какая из формул называется формулой трапеций:

a);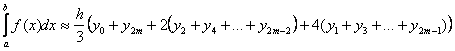

b);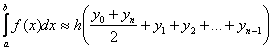

c).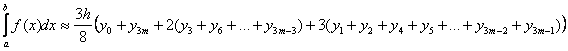

 6.      Какая из формул называется формулой Ньютона:

a);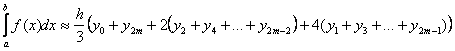

b);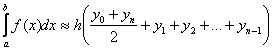

c).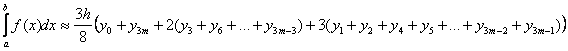

Критерии оценки

 

Оценка	Количество правильных ответов
«Отлично»	6
«Хорошо»	5
«Удовлетворительно»	4
«Неудовлетворительно»	Менее 4

 

 

4.2. Задания промежуточной аттестации

4.2.1. Перечень вопросов к экзамену

 

1.Значение математики в профессиональной деятельности и при освоении ППССЗ Основные математические методы решения прикладных задач в области профессиональной деятельности.  Основные понятия  и методы математического анализа.

2.Определение функции. Свойства функций.

3. Графики функций. Способы задания функций. Элементарные функции

4. Предел функций. Бесконечно малые и бесконечно большие функции.

5. Основные теоремы о пределах функций. Замечательные пределы.

6. Непрерывность функций. Точки разрыва.

7. Производная функции. Таблица основных формул дифференцирования

8. Производная функции. Ее геометрический и механический смысл Таблица основных формул дифференцирования

9.Производная сложной функции. Производная:   решение прикладных задач в области профессиональной деятельности

10. Таблица основных формул дифференцирования

11. Дифференциал функции и его приложение к решению задач

12.  Признаки возрастания и убывания функции

13. Экстремумы функции

14. Выпуклость графика функции. Точки перегиба

15. Асимптоты кривой

16. Схема исследования функции

17. Первообразная. Неопределенный интеграл.

18. Таблица интегралов. Методы интегрирования.

19. Приложение определенного интеграла.

20. Определенный интеграл и его геометрический смысл.

21. Основные понятия линейной алгебры. Матрицы.

21. Вычисление площадей плоских фигур с помощью определенного интеграла.

22.Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения (виды, способы решения). Основные понятия

23. Дифференциальные уравнения первого порядка с разделяющимися переменными

24. Линейное дифференциальное уравнение II порядка с постоянными коэффициентами. Теорема Коши.

25. Основные понятия линейной алгебры. Решение систем линейных уравнений. Прикладные задачи в области профессиональной деятельности

26. Матрицы.Операции над матрицами.  Невырожденная матрица.

 27. Основные понятия линейной алгебры. Матрицы. Обратная матрица. Ранг   матрицы.

 28. Определитель n-го порядка. Свойства определителей. Алгебраические  миноры. Вычисление определителей.

29. Методы решения систем линейных уравнений. Метод Крамера.

30.  Методы решения систем линейных уравнений. Метод Гаусса

31. Методы решения систем линейных уравнений. Матричный метод.

32.  Понятие числа. Натуральные, целые и рациональные числа. Вещественные числа.

33. Основные понятия теории комплексных чисел. Понятие комплексного числа. Алгебраическая форма комплексного числа.

34. Действия над комплексными числами, записанных в тригонометрической форме.

35. Решение квадратных уравнений с действительными коэффициентами.

36.  Модуль и аргумент комплексного числа.

37. Тригонометрическая форма комплексного числа. Действия над комплексными числами.

38.  Действия над комплексными числами, заданными в тригонометрической форме. Формула Муавра

39.  Формула Эйлера. Показательная форма комплексного числа.

40. Показательная форма комплексного числа. Действия над комплексными числами.

41.  Основные понятия теории вероятностей. Понятие события и вероятности события

42.  События. Виды событий. Классическое определение вероятности

43.  Теорема сложение и умножения вероятностей

44.  Случайные величины. Числовые характеристики случайных величин

45. Случайная величина.

46. Дискретная случайная величина

47. Закон распределения случайной величины

48. Математическое ожидание и дисперсия случайной величины

49. Основные понятия математической статистики. Выборка. Представление данных.

50. Основные понятия математической статистики. Основные показатели вариации.

51. Основы интегрального исчисления. Формулы прямоугольников.

52. Основы интегрального исчисления. Метод трапеций

53. Основы интегрального исчисления. Формулы Симпсона.

54.Основы интегрального исчисления. Абсолютная погрешность при численном интегрировании 

55. Основы дифференциального исчисления. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. Погрешность в  определении производной.

56. Основы дифференциального исчисления. Погрешность в  определении

 

4.2.2. Перечень практических заданий к экзамену

 

1.Два генератора, которые дают  (при стандартной частоте) соответственно напряжение u₁=220sin(wt+60⁰) и u₁=127sin(wt-90⁰), соединены  последовательно. Определить напряжение на зажимах цепи, т.е. суммарное напряжение.

2.Исследовать функцию на монотонность и экстремумы 

3. Вычислить определители:

 .

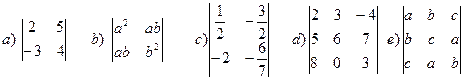4. В бригаде  из 30  рабочих нужно выбрать заместителя бригадира,  физорга, профорга. Сколькими способами это  можно сделать, если каждый рабочий член профсоюза и спортсмен.

5. Решите уравнение

6. Найти: 1) математическое ожидание М(Х); 2) дисперсию D(X)

 

Х	52	54	57	51
р	0,1	0,4	0,3	0,2

 

 

7. Точка движется по координатной прямой по закону s(t) = -t²+10t-7. Найдите v_мнг(3).

8. Из группы руководителей , состоящей из 10 юношей и 8 девушек, выбирают по жребию 4 специалистов. Какова вероятность того, что в числе избранных окажутся двое юношей и две девушки?

9.Найти значение определенных интегралов      .

10. Найти значение неопределенного интеграла.

11. Найти: 1) математическое ожидание М(Х); 2) дисперсию D(X)

 

12. Вычислить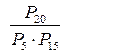

13.Двое рабочих получили за зарплату 765тыс рублей. Первый работал 10 дней. А второй 9 дней. Сколько получал в день каждый из них, если известно, что первый рабочий за 5 дней получил на 45 тыс рублей больше, чем второй за три дня? Решите задачу  методом Крамера

14. Найти площадь нефтяного объекта, ограниченного линиями 

15. . Оцените погрешность работы нефтяного насоса по формуле прямоугольников, используя определенный интеграл .

 

.16.Вычислить пределы

 17. Решите уравнение

18.Найти производную функции, заданной таблично в точке .

х	y
30	1,4771
35	1,5441
40	1,6021
45	1,6532
50	1,6990

 

 

 

 

 

 

 

 

 

 

 

19. Исследовать функцию на экстремумы и монотонность  

20. Вычислите определители:

.

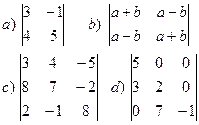
21. .   Найти сумму  и  произведение матриц:

а) А = ,  В =

 

22. Вращающейся в жидкости диск замедляет свою угловую скорость за счет трения. Известно, что трение пропорционально угловой скорости. Определить с какой скоростью будет вращаться диск в момент  t=4мин, если при t=0 он делает 120 об/мин, а при t=1 мин его скорость стала80 об/мин.

23. Найдите уравнение касательной к графику функции f(x)=-x² -4x+2 в точке с абсциссой x₀=-1.

24. Экономист, интересующийся тарифным разрядом рабочих некоторого подразделения  нефтяного завода,  выбрал документы 20 рабочих и выписал из них последовательность разрядов:1,2,5,6,6,6,2,3,5,4,6,3,4,4,6,6,5,1,3,5.Сгруппируйте ряд данных, постройте в системе координат полигон относительных частот и гистограмму.

25. Найти значение определенных интегралов    .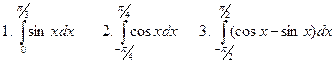

26.  В ящике имеется 12 деталей, из которых 5 деталей нестандартные.  Сборщик наудачу извлекает из ящика 4 детали. Какова вероятность того, что две будут нестандартными?

27. .    Выполнить действия в алгебраической форме записи:

а) ;         б) ;        в)

28. Найти значение определенных интегралов     

 

 

 

 

Критерии оценки:

Оценка за ответ на теоретический вопрос:

Отметкой «5»

-       Студент полно раскрыл содержание материала в объеме, предусмотренном программой;

-       изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

-       правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

-       показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;

-       продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при отработке умений и навыков;

-       отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые студент  легко исправил по замечанию преподавателя.

 

Отметка «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

-       в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

-       допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию преподавателя;

-       допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию преподавателя.

 

Отметка «3» ставится в следующих случаях:

-       неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала;

-       имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя;

-       студент не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

-       при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков

Отметка «2» ставится в следующих случаях:

-       не раскрыто основное содержание учебного материала;

-       обнаружено незнание или непонимание студентом большей или наиболее важной части учебного материала;

-       допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов преподавателя.

 

Оценка за ответ на практический вопрос:

Отметка «5» ставится, если:

-       задание  выполнено полностью;

-       в логических  рассуждениях и обосновании решения нет пробелов и ошибок; 

-       в решении нет математических ошибок

           Отметка «4» ставится, если:

-       задание выполнено полностью, но обоснования шагов решения недостаточны

-       допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках

          Отметка «3» ставится, если:

-       допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но студент  владеет обязательными умениями

           Отметка «2» ставится, если:

-       допущены существенные ошибки, показавшие, что студент не владеет обязательными умениями .

 

5. Перечень используемых материалов, оборудования и информационных источников

 

Основные источники:

Для обучающихся

1. Богомолов Н.В. Практические занятия по математике. - М.: Высш. шк., 2017. - 495 с.

2. Валуцэ И.И. Математика для техникумов. - М.: Наука. Гл. ред. Физ.-мат. Лит., 2017 - 576 с.

3. Пехлецкий И.Д. Математика. Учебник – 2-е изд., стереотип.- М.: Издательский центр «Академия»; Мастерство, 2016.-304 с.

Информационные ресурсы

1.      http://mathem.hl/ru/

2.      http://math.child.ru/

3.      http://zadachi.mccme.ru/

4.      http://mschool.kubsu.ru/

5.      http://sumik.open-edu.ru/SUMIK/e-SUMIK-Matematika.index.HTM  и др.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru

---