Министерство образования и науки Челябинской области

государственное бюджетное профессиональное образовательное         учреждение

«Каслинский промышленно - гуманитарный техникум»

Верхнеуфалейский филиал

 

 

 

 

КОМПЛЕКТ КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ

 

 

по учебной дисциплине

ЕН.01. «Математика »

По специальности 15.02.08 «Технология машиностроения»

 

 

 

 

Форма обучения: очная

Курс обучения: 2 курс (3 семестр)

 

 

 

 

 

 

 

 

2019год

 

СОГЛАСОВАНО  на заседании предметно-цикловой комиссии Протокол № ____ от «___» ___________ 2019  г. Председатель ПЦК: _________

УТВЕРЖДАЮ: Зам.директора по учебной работе  ГБПОУ «КПГТ» _____________ Н.Н. Ефанова

 

Организация – разработчик: Государственное бюджетное профессиональное образовательное учреждение «Каслинский промышленно-гуманитарный техникум» Верхнеуфалейский филиал

 

 

Разработчик: Хусаинов В.Г., преподаватель ГБПОУ «Каслинский промышленно-гуманитарный техникум» Верхнеуфалейский филиал

 

 

 

СОДЕРЖАНИЕ

 

1	Паспорт комплекта контрольно-оценочных средств	4
2	Результаты освоения учебной дисциплины	4
3	Оценка освоения учебной дисциплины	5
3.1	Формы контроля и оценивания элементов учебной дисциплины	7
3.2	Типовые задания для оценки освоения учебной дисциплины	10
3.2.1	Входной контроль	10
3.2.2	Задания для промежуточного тематического контроля (контрольные работы).	15
3.2.3	Задания для итогового контроля (экзамен).	40
4	Критерии оценивания.	43
5	Учебно-методическое и информационное обеспечение дисциплины	47

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.Паспорт комплекта контрольно – оценочных срезов

 

Контрольно-оценочные средства предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины   ЕН.01 «Математика»

Косы включают контрольные материалы для проведения  промежуточного контроля и итоговой аттестации в форме экзамена.

Косы разработаны на основании:

основной профессиональной образовательной программы по направлению подготовки по специальности 15.02.08 «Технология машиностроения»

программы учебной дисциплины Математика.

2.Результаты освоения учебной дисциплины

 

В результате освоения учебной дисциплины обучающийся должен обладать общими компетенциями, включающими в себя способность(для данной профессии или специальности)

 ОК 1. Понимать сущность и социальную значимость своей будущей профессии,

проявлять к ней устойчивый интерес.

ОК 2. Организовывать собственную деятельность, определять методы и способы

выполнения профессиональных задач, оценивать их эффективность и

качество. 
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных

ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для

постановки и решения профессиональных задач, профессионального и

личностного развития.

ОК 5. Использовать информационно-коммуникационные технологии для

совершенствования профессиональной деятельности.

ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно

общаться с коллегами, руководством, клиентами.

ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и

контролировать их работу с принятием на себя ответственности за результат

выполнения заданий.

ОК 8. Самостоятельно определять задачи профессионального и личностного

развития, заниматься самообразованием, осознанно планировать

повышение квалификации.

ОК 9. Быть готовым к смене технологий в профессиональной деятельности. 
ОК 10. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей).

 

3.Оценка освоения учебной дисциплины

Результатом освоения дисциплины является получение (освоение) знаний и умений

Результаты обучения

(освоенные умения, усвоенные знания)

Показатели оценки результата

Умения:

решать линейные и квадратные уравнения и уравнения, сводящиеся к ним;

получение корней линейных и квадратных уравнений и уравнений, сводящихся к ним, обоснование выбора формул для решения квадратных уравнений и неполных квадратных уравнений;

выполнять действия с действительными числами, пользоваться калькулятором для вычислений, находить приближённые вычисления;

выполнение действий с действительными числами, демонстрация умений использования калькулятора для вычислений и нахождения приближённых вычислений;

решать линейные и квадратные неравенства, системы неравенства;

изложение основных этапов решения линейных и квадратных неравенств и их систем;

производить действия с векторами;

формулирование правил сложения и вычитания векторов, демонстрация умений выполнения действий над векторами;

использовать свойства элементарных функций при решении задач и упражнений;

изложение свойств функций и демонстрация понимания их использования при решении задач и упражнений;

выполнять тождественные преобразования со степенными, логарифмическими и тригонометрическими выражениями;

применение тождественных преобразований над степенными, логарифмическими и тригонометрическими выражениями; обоснование выбора формулы или свойства функций для преобразования;

строить графики показательных, логарифмических и тригонометрических функций, выполнять их преобразования;

создание графиков показательных, логарифмических и тригонометрических функций, демонстрация умений выполнения преобразований графиков таких функций;

вычислять производные и первообразные, определённые интегралы, применять определённый интеграл для нахождения площади криволинейной трапеции;

получение производных и первообразных некоторых функций, построение криволинейной трапеции, нахождение её площади с помощью определённого интеграла;

применять свойства прямых и плоскостей в пространстве при решении задач;

обоснование свойств прямых и плоскостей в пространстве при решении задач;

изображать геометрические тела на плоскости и в пространстве, строить их сечения плоскостью;

демонстрация умений построения геометрических тел и их сечений на плоскости и в пространстве;

решать задачи на вычисление площадей поверхностей и объёмов геометрических тел;

определение формулы для вычисления площадей и объёмов геометрических тел, применение их для решения задач;

уметь применять основные положения теории вероятностей и математической статистики в профессиональной деятельности.

выделение основных элементов теории вероятностей и математической статистики, решение практических задач.

Знания:

 

основные функции, их графики и свойства;

перечисление основных функций, формулирование их свойств, описание процесса построения графиков;

основы дифференциального и интегрального исчислений;

формулирование правил и формул дифференциального и интегрального исчислений;

алгоритмы решения тригонометрических, показательных, логарифмических уравнений и неравенств;

изложение алгоритмов решения тригонометрических, показательных и логарифмических уравнений и неравенств;

основные свойства элементарных функций;

определение основных свойств элементарных функций;

основные понятия векторной алгебры;

формулирование определений и выделение основных понятий векторной алгебры;

основы линейной алгебры;

обоснование основных понятий линейной алгебры;

основные понятия и определения стереометрии;

узнавание геометрических тел, формулирование основных понятий и определений стереометрии;

свойства геометрических тел и поверхностей;

перечисление свойств геометрических тел и их поверхностей;

формулы площадей поверхностей и объёмов;

выделение формул площадей поверхностей и объёмов;

основные понятия комбинаторики; статистики, теории вероятностей.

изложение основных понятий комбинаторики, статистики и теории вероятностей.

 

 

 

3.1.Формы контроля и оценивания элементов учебной дисциплины

Типы заданий для текущего контроля и критерии оценки

 

Контроль  за результатами обучения осуществляется через проведение специальных уроков оценки знаний, практических занятий, использование в практической деятельности критериев оценки интеллектуальных особенностей обучающихся. Применяются следующие виды контроля: вводный, текущий, тематический, итоговый, первичной проверки знаний, обучающий. Формы контроля: устный опрос; устный фронтальный опрос; составление опорного конспекта; работа с карточками; диктант; кроссворд;  самостоятельное решение упражнений с последующей самопроверкой по готовым ответам и указаниям к решению; самостоятельная работа; тест; домашняя практическая работа; контрольный тест; контрольная работа.

Формы и методы текущего контроля, промежуточной аттестации по учебной дисциплине доводятся до сведения обучающихся в начале обучения. Для текущего контроля по программе создан фонд контрольно-оценочных средств (ФКОС).

ФКОС включают в себя педагогические контрольно-измерительные материалы, предназначенные для определения соответствия (или несоответствия) индивидуальных образовательных достижений основным показателям результатов подготовки.

Контроль и оценка результатов содержит 20 контрольных точек, обеспечивающих текущий контроль.

Промежуточная аттестация проводится в конце 2 семестра в форме экзамена.  Оценка результатов освоения программы происходит с использованием пятибалльной системы оценивания знаний. Используются следующие критерии оценки:

Оценка	Критерий
«5»	Работа выполнена в заданное время, самостоятельно, с соблюдением определенных требований, качественно и творчески
«4»	Работа выполнена в заданное время, самостоятельно, с соблюдением определенных требований, при выполнении отдельных алгоритмов действий допущены небольшие отклонения, общий вид объекта достаточно аккуратный
«3»	Работа выполнена в заданное время, самостоятельно, с нарушением заданной последовательности, отдельные алгоритмы действия выполнены с отклонением от образца, объект оформлен небрежно или не в заданный срок
«2»	Обучаемый самостоятельно не справился с работой, последовательность нарушена, при выполнении алгоритмов действия допущены большие отклонения, объект оформлен небрежно и имеет незавершенный вид

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

·                 работа выполнена полностью;

·                 в логических рассуждениях и обосновании решения нет пробелов и ошибок;

·                 в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

·                  работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

·                  допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

·                  допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

 Отметка «2» ставится, если:

·  допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

·  работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Преподаватель  может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Ответ оценивается отметкой «5», если ученик:

·                 полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

·                 изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

·                 правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

·                 показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

·                 продемонстрировал знание теории ранее изученных сопутствующих тем,  сформированность и устойчивость используемых при ответе умений и навыков;

·                 отвечал самостоятельно, без наводящих вопросов преподавателя;

·                 возможны одна – две  неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания преподавателя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

·                  в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

·                  допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания преподавателя;

·                  допущены ошибка или более двух недочетов  при освещении второстепенных вопросов или в выкладках,  легко исправленные после замечания преподавателя.

Отметка «3» ставится в следующих случаях:

·                 неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

·                 имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя;

·                 студент не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

·                 при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

 Отметка «2» ставится в следующих случаях:

·  не раскрыто основное содержание учебного материала;

·  обнаружено незнание учеником большей или наиболее важной части учебного материала;

·  допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

 

3. Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

·                     незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов  

обозначений величин, единиц их измерения;

·                     незнание наименований единиц измерения;

·                     неумение выделить в ответе главное;

·                     неумение применять знания, алгоритмы для решения задач;

·                     неумение делать выводы и обобщения;

·                     неумение читать и строить графики;

·                     неумение пользоваться первоисточниками, учебником и справочниками;

·                     потеря корня или сохранение постороннего корня;

·                     отбрасывание без объяснений одного из них;

·                     равнозначные им ошибки;

·                     вычислительные ошибки, если они не являются опиской;

·                      логические ошибки.

  К негрубым ошибкам следует отнести:

·                     неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

·                     неточность графика;

·                     нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

·                     нерациональные методы работы со справочной и другой литературой;

·                     неумение решать задачи, выполнять задания в общем виде.

  Недочетами являются:

·                     нерациональные приемы вычислений и преобразований;

·                     небрежное выполнение записей, чертежей, схем, графиков.

 

 

3.2.

ВХОДНОЙ КОНТРОЛЬ        Выполните тестовое задание. Общие рекомендации по выполнению теста: 1. Внимательно прочитайте задание, выберите правильные варианты ответа. 2. Задание выполняется в аудитории и сдается для проверки отчет теста.   1. Если матрица , то матрица 4A имеет вид: А) ; б) ; в) ; г) ; д) .   2. Если матрицы  и, то матрица 3A – 2B имеет вид: А) ; б) ; в) ; г) ; д) .   3. Указать те преобразования строк (столбцов) матрицы, которые являются элементарными: а) умножение строки (столбца) на ненулевое число; б) замена элементов строки (столбца) произвольными числами; в) замена строки (столбца) суммой этой строки (столбца) и другой строки (столбца), предварительно умноженной на некоторое число; г) поменять местами две строки (два столбца); д) замена строки (столбца) нулевой строкой (столбцом); е) транспонирование матрицы.   4. При умножении матрицы A на матрицу B справа должно соблюдаться условие:  а) число строк матрицы A равно числу строк матрицы B;    б) число строк матрицы A равно числу столбцов матрицы B;    в) число столбцов матрицы A равно числу столбцов матрицы B;    г) если матрицы не квадратные, то они должны быть одинакового размера;    д) верный ответ отсутствует.   5. Квадратная матрица называется диагональной, если а) элементы, лежащие на побочной диагонали, равны нулю;   б) элементы, лежащие на главной диагонали, равны нулю;   в) элементы, не лежащие на главной диагонали, равны нулю;    г) элементы, лежащие ниже главной диагонали, равны нулю;   д) элементы, лежащие на главной диагонали, обязательно равны.   6. Установить соответствие между парой матрицей A и B и их произведением A · B:   Матрицы А и В А) , Б) В) Г) ,     7. Если матрицы и,  то определитель матрицы A·B равен: а) 0; б) -16;  в) 32;  г) 2;   д) -32.       8. Распределите матрицы в порядке увеличения их определителей:     9. Если матрица системы n уравнений квадратная и ее определитель не равен нулю, то система  а) не имеет решений;    б) имеет единственное решение;    в) имеет не более n решений;    г) имеет ровно n решений;    д) имеет бесконечно много решений.   10. При решении системы по правилу Крамера используют формулы а) ; б) ; в) ; г) ; д) . 11. Найти значение b, при котором система совместна     12. При решении системы  по правилу Крамера: а) ;   б) ;   в) ;   г) ;   д) .       Эталон ответов для теста №1: Номер задания 1 2 3 4 5 6 7 8 9 10 11 12 Вариант ответа в д а, в, г в в А Б  В  Г 3 5  1   2 д 4; 1; 3; 5; 2 б в 3 б

 

 

 

 

 

 

 

3.2.2 Задания для промежуточного тематического контроля

(контрольные работы).                                                                                               

 

 

Раздел 1. Контрольная работа №1 « Решение системы уравнений различными методами»

 

Вариант   №1

 
 1. Вычислить линейную комбинацию матриц А и В:

Дано: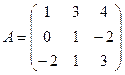, 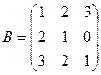. Найти: 3А – 2В.

2. Вычислить произведение матриц:

а).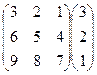

б) .

3. Найти матрицу, обратную данной: A=.

4. Вычислить определитель .

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

 .

7. Методом Гаусса исследовать совместность и найти общее решение
системы:

а)

;

б)

;

в)

ВАРИАНТ № 2

 

1. Вычислить линейную комбинацию матриц А и В.

Дано:, . Найти: 3А – 2В.

2. Вычислить произведение матриц: .

3. Найти матрицу, обратную данной: A=.

4. Вычислить определитель, используя подходящее разложение по строке или столбцу

.

5. Вычислить ранг матрицы .

6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:

.

 

 

 Решения

Задача 1.Вычислить линейную комбинацию матриц А и В.

Дано:, .

Найти: 3А – 2В.

Решение

1. Найдем 3А и 2В - произведения матриц на число, умножая каждый элемент матриц на соответствующее число:

;

.

2. Вычислим поэлементно искомую разность полученных матриц:

.

Ответ: .

Задача 2. Вычислить произведение матриц:

а).

Решение

1. Определим размер матрицы-произведения: .

2. Найдем элементы с_ij матрицы-произведения как сумму произведений элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В:

 

 

 

.

Ответ:.

б) .

Решение

1. Определим размер матрицы-произведения: .

2. Найдем элементы с_ij матрицы-произведения С:

 

.

 

Ответ: .

Задача 3. Найти матрицу, обратную данной: A=.

Решение

Для нахождения обратной матрицы воспользуемся формулой:

 

, (1)

 

где

­ detA - определитель матрицы А;

­ - присоединенная матрица, составленная из алгебраических дополнений элементов матрицы А;

­ * - символ транспонирования матрицы.

1. Вычислим определитель матрицы:

Определитель матрицы , следовательно, матрица А – невырожденная и обратная матрица существует.

2. Составим присоединенную матрицу

,

где - алгебраические дополнения, - миноры элементов матрицы А, связь между которыми выражается формулой:

. (2)

Минор элемента определяется как определитель, получающийся из исходной матрицы вычеркиванием строки и столбца, на пересечении которых находится элемент.

3. Транспонируем матрицу , т.е. поменяем местами строки и столбцы матрицы:

.

4. Вычислим обратную матрицу по формуле (1):

.

5. Сделаем проверку. Согласно определению обратной матрицы

, (3)

где Е – единичная матрица.

Вычислим произведение :

.

Аналогично можно показать, что выполняется равенство .

Ответ: .

Задача 4. Вычислить определитель .

Решение

Для вычисления определителя четвертого порядка используем теорему о разложении определителя, согласно которой определитель n –го порядка Δ равен сумме произведений элементов какой-либо строки или какого либо столбца на их алгебраические дополнения, т.е.:

, ; (4)

или

,  (5)

где - алгебраические дополнения элементов; i – номер строки, j – номер столбца определителя Δ.

Разложим исходный определитель четвертого порядка (n = 4) по элементам второго столбца (j = 2), тогда формула (5) для вычисления определителя принимает вид:

. (6)

Пользуясь свойствами определителей, упростим вычисление определителя по формуле (6), обратив в нули все элементы второго столбца, кроме элемента . Чтобы получить нули во втором столбце определителя, прибавим элементы первой строки (умноженные на 1) к соответствующим элементам второй и четвертой строк и вычтем из соответствующих элементов третьей строки:

 

.

 

Вычисляя полученный преобразованный определитель по формуле (6), получим:

Таким образом, вычисление определителя четвертого порядка свелось к вычислению одного определителя третьего порядка, который можно вычислить, например, методом треугольников, а можно опять понизить порядок определителя, используя теорему разложения.

Применим второй способ, предварительно преобразовав определитель третьего порядка. Обратим в нули все элементы третьего столбца определителя, кроме элемента . Для этого сначала умножим все элементы первой строки на 3 и сложим их с соответствующими элементами второй строки, затем все элементы первой строки сложим с соответствующими элементами третьей строки.

.

Раскладывая определитель по элементам третьего столбца, и вынося общие множители, получим:

.

Ответ:16.

Задача 5. Вычислить ранг матрицы .

Решение

1. Определим интервал, в котором находятся значения ранга данной матрицы. Известно, что для ранга матрицы А размера mxn справедливо соотношение:

, (7)

в соответствии с которым ранг исходной матрицы размера 3х4 лежит в интервале:или .

2. Для вычисления ранга матрицы воспользуемся методом элементарных преобразований, в соответствии с которым исходная матрица приводится к трапециевидной (ступенчатой) форме.

Приведем исходную матрицу к трапециевидной форме. Для этого на первом этапе получим нули в первом столбце матрицы, умножая элементы первой строки сначала на (-2), затем на (-5) и складывая их с соответствующими элементами второй и третьей строки:

®.

На втором этапе получим нули во втором столбце матрицы. Сначала для удобства дальнейших преобразований умножим элементы второй и третьей строки на (-1), а затем умножим элементы второй строки на (-2) и прибавим к соответствующим элементам третьей строки:

.

Ранг полученной трапециевидной матрицы равен числу главных диагональных элементов (в данном случае – единиц), отличных от нуля, т.е. rang(A) = 2.

Ответ: 2.

Задача 6. Решить систему с помощью формул Крамера

.

Решение

Формулы Крамера имеют вид:

, (D ≠ 0; j = 1,2,…,n) (8)

где

­ - неизвестные, n – число неизвестных;

­ D – главный определитель системы, составленный из коэффициентов при неизвестных,

­ D_j- вспомогательный определитель, получающийся из главного определителя D заменой j –го столбца на столбец свободных членов.

1. Вычислим определители (например, методом треугольников):

- главный определитель;

вспомогательные определители

, , .

2. Так как главный определитель системы отличен от нуля (D ≠ 0), то система имеет единственное решение, которое может быть найдено по формулам Крамера (8):

,

,

.

Целесообразно сделать проверку полученного решения. Подставим найденные значения неизвестных в исходную систему:

.

При подстановке найденных значений неизвестных в исходную систему каждое уравнение системы обратилось в тождество, следовательно, найденная последовательность чисел является решением системы.

Ответ: .

Задача 7.Решить методом Гаусса систему

а)

.

Решение

1. Определим число неизвестных системы n = 4 и число уравнений m = 4.

Выпишем матрицу коэффициентов системы 
и матрицу-столбец свободных членов .

Составим расширенную матрицу системы - матрицу коэффициентов, дополненную столбцом свободных членов

= .

2. Приведем расширенную матрицу системы к трапециевидной форме (прямой ход метода Гаусса). Для этого, умножая элементы первой строки на числа (-2),(-3),(-4) и прибавляя их к соответствующим элементам второй, третьей, четвертой строки соответственно, получим нули в первом столбце матрицы. Затем, подбирая соответствующие множители ко второй и третьей строкам, получим нули во втором и третьем столбцах матрицы:

=®

®®®

3. [1]Определим ранги матриц:

rang = rang= 4 – ранг расширенной матрицы;

rang== 4 ранг матрицы коэффициентов системы.

rang= rang = r = 4.

Ранг матрицы коэффициентов системы равен рангу расширенной матрицы и равен числу неизвестных системы (r = n =4). В этом случае, согласно теореме Кронекера-Капелли, система имеет единственное решение.

4. Найдем решение системы (обратный ход метода Гаусса):

Запишем укороченную систему, соответствующую полученной трапециевидной матрице:

. 

Найдем неизвестные, последовательно исключая переменные

из уравнения (4′) x₄ = 1,

из уравнения (3′) x₃ = 0+x₄ = 0 + 1 = 1,

из уравнения (2′) x₂=10 – 2x₃ – 7x₄ = 10 – 2 – 7 = 1,

из уравнения (1′) x₁ = 11 – 2x₂ – 3x₃ – 4x₄ = 11 – 2 – 3 – 4 = 2.

Ответ: система совместна, определена,
имеет единственное решение .

б)

.

Решение

m = 3; n = 3.

1. Приведем расширенную матрицу системы к трапециевидной форме (прямой ход метода Гаусса):

.

В процессе преобразований на первом шаге поменяли местами первый и третий столбцы матрицы; на втором и третьем шагах получили нули в первом и втором столбцах соответственно.

Исходя их вида полученной трапециевидной матрицы, можно сделать вывод о том, что система несовместна (т.е. не имеет решений), так как последняя строка матрицы содержит ненулевой свободный член и соответствует противоречивому уравнению, которое привело к неверному равенству 0 = 1.

Заметим, что в данном случае ранг расширенной матрицы не равен рангу матрицы коэффициентов системы rang≠ rang и, в соответствии с теоремой Кронекера-Капелли, такая система несовместна.

Ответ: система несовместна.

в)

Решение

m = 3; n = 4.

Заметим, что в данном случае число уравнений меньше числа неизвестных (m < n), и такая система не может быть определена, т.е. не может иметь единственное решение.

1. Приведем расширенную матрицу системы к трапециевидной форме (прямой ход метода Гаусса):

.

2.Ранг полученной трапециевидной матрицы r, равный числу единиц, стоящих на главной диагонали, равен рангу матрицы коэффициентов системы, т. е. в этом случае

rang = rang= r = 2

и система совместна.

Так как r < n (ранг меньше числа неизвестных), система не определена, т.е. имеет бесконечное множество решений.

Так как r = 2, то две переменные х₁ и х₂, входящие в базисный минор, являются базисными, остальные (n – r) переменные – свободные.

Пусть свободные переменные х₃ и х₄ принимают произвольные числовые значения С₁ и С₂ , т.е. положим:

 .

3. Обратный ход метода Гаусса. Запишем укороченную систему, соответствующую полученной трапециевидной матрице:

Оставим базисные переменные х₁ и х₂ в левой части уравнений, а свободные переменные х₃ и х₄ перенесем в правую часть:

,

где ; ,

откуда

,

.

Запишем общее решение системы в виде вектор-функции от свободных переменных С₁ и С₂

.

Ответ: .

 

 

 

 

 

 

 

 Контрольная работа №2 по теме «Основы дифференциального интегрального исчисления»

Вариант № 1

 

Задание1. Даны функция z=z(x,y), точка A(x0;y0) и вектор a(ax;ay). Найти: 1) grad z в точке А. 2) производную в точке А по направлению вектора a.

 

 

Решение:

 

1)

;

 

2) Производная по направлению:

 

Задание 2. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (a>0).

 

 

Решение:

Преобразуем формулу в полярные координаты:

 

 

Задание 3. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями.

 

Тело, объем которого мы находим ограничено сверху z=, а снизу z=0,

х и y изменяются от 0 до 4.

 

 

Задание 4. Исследовать сходимость числового ряда

 

 

По признаку Даламбера:

, значит ряд расходится.

 

Задание 5. Найти интервал сходимости степенного ряда

 

 

Решение:

 

 

Интервал сходимости:

(-1< x < 1)

Вариант№2

Задание 1. Вычислить определенный интеграл с точностью до 0.001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировать его почленно.

 

 

Разложим подынтегральную функцию применяя таблицу простейших разложений:

 

Проинтегрируем ряд почленно:

 

Задание 2. Разложить данную функцию f(x) в ряд Фурье

 

 

Решение:

 

 

Задание 3. Найти общее решение дифференциального уравнения

 

 

Решение:

 

;

1.

 интегрируем обе части

интегрируем обе части

Искомая функция:

 

Задание 4. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям

 

 

Это линейное неоднородное дифференциальное уравнение II порядка. Составим характеристическое уравнение:

 

 

Т.к. корни действительные и одинаковые, то общее решение соответствующего однородного уравнения запишем в виде

 

интеграл функция дифференциальное уравнение

Правая часть уравнение может быть представлена в виде:

 

, где

 

Является корнем характеристического уравнения кратности 2.

Частное решение исходного уравнения будем искать в виде

Найдем первую и вторую производные частного решения, подставим их в исходное дифференциальное уравнение и приравняем коэффициенты при одинаковых степенях переменной х.

 

; А=5

Следовательно общее решение исходного (неоднородного) уравнения запишем в виде:

 

Найдем частное решение:

Частное решение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.2.3

ЗАДАНИЯ ДЛЯ ИТОГОВОГО КОНТРОЛЯ (ЭКЗАМЕН).

 

Вариант 1

Тема 1. Решение систем линейных уравнений:

Тема 2. Векторы и координаты

Найдите  скалярное произведение векторов   а и в, если =3, =1, =45

Тема 3. Функции, пределы, последовательности

Найдите предел последовательности  

+6n

           n                    (2n+1)*(8n+1)

Тема 4. Техника дифференцирования.

Найдите производную функции  y = 2^x - arctg x

 

 Тема 5. Применение  дифференциального исчисления для исследования функции

Найдите наибольшее и наименьшее значение функции f(x) = x⁴-8x²-9  на отрезке

 

Тема 6. Неопределенный интеграл и его свойства

Для функции f(x) = cos²x  найти  ту  первообразную, график которой проходит через точку

М (/2; /4)

 

Тема 7. Определенный интеграл

 Вычислить определенный интеграл

⁴ x dx

 

Тема 8. Применение интеграла к вычислению площадей

Найдите площадь фигуры, ограниченной линиями  x=0,   x=/2,  f₁(x) = sin x, f₂(x) = cos x

 

Тема 9. Основные теоремы теории вероятностей

Найдите член  разложения  (x+ ₄)¹⁰,   не содержащий х (т.е. содержащий х в нулевой степени)

 

Тема 10. Случайные величины и их законы распределения

Найдите вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.

Вариант 2

Тема 1. Решение систем линейных уравнений

Тема 2.  Векторы и координаты

Найдите  угол  между векторами

a     и    в =

Тема 3. Функции, пределы, последовательности

Найдите предел последовательности  

             

 

Тема 4. Техника дифференцирования

 Вычислите:

f^/ (, если f(x) = 5 arcsin x - 3 arсcos x 

 

 Тема 5. Применение  дифференциального исчисления для исследования функции

Найдите наибольшее и наименьшее значение функции y =  4

на интервале 

 

Тема 6. Неопределенный интеграл и его свойства

 Найдите все первообразные функции  y = x+2,  касающиеся  кривой  y = x²

Тема 7. Определенный интеграл:

 Вычислить  интеграл

 

Тема 8. Применение интеграла к вычислению площадей

Найдите площадь фигуры, ограниченной линиями   y=² ,  y=0

 

Тема 9. Основные теоремы теории вероятностей

Найдите шестой член  разложения  (y^1/2+ x^1/3)ⁿ,    если биноминальный коэффициент третьего от конца члена равен 45

 

Тема 10. Случайные величины и их законы распределения

Найдите вероятность того, что на удачу взятое двузначное число окажется   кратным либо 3, либо 5, либо тому и другому одновременно.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РАЗДЕЛ 4.  Критерии оценивания.

 

 

Промежуточная аттестация проводится в конце 2 семестра в форме экзамена.  Оценка результатов освоения программы происходит с использованием пятибалльной системы оценивания знаний. Используются следующие критерии оценки:

Оценка	Критерий
«5»	Работа выполнена в заданное время, самостоятельно, с соблюдением определенных требований, качественно и творчески
«4»	Работа выполнена в заданное время, самостоятельно, с соблюдением определенных требований, при выполнении отдельных алгоритмов действий допущены небольшие отклонения, общий вид объекта достаточно аккуратный
«3»	Работа выполнена в заданное время, самостоятельно, с нарушением заданной последовательности, отдельные алгоритмы действия выполнены с отклонением от образца, объект оформлен небрежно или не в заданный срок
«2»	Обучаемый самостоятельно не справился с работой, последовательность нарушена, при выполнении алгоритмов действия допущены большие отклонения, объект оформлен небрежно и имеет незавершенный вид

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

·                     работа выполнена полностью;

·                     в логических рассуждениях и обосновании решения нет пробелов и ошибок;

·                     в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

·                     работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

·                     допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

·                      допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

 Отметка «2» ставится, если:

·                     допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

·                     работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Преподаватель  может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Ответ оценивается отметкой «5», если ученик:

·                     полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

·                     изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

·                     правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

·                     показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

·                     продемонстрировал знание теории ранее изученных сопутствующих тем,  сформированность и устойчивость используемых при ответе умений и навыков;

·                     отвечал самостоятельно, без наводящих вопросов преподавателя;

·                     возможны одна – две  неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания преподавателя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

·                     в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

·                     допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания преподавателя;

·                     допущены ошибка или более двух недочетов  при освещении второстепенных вопросов или в выкладках,  легко исправленные после замечания преподавателя.

Отметка «3» ставится в следующих случаях:

·                     неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

·                     имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя;

·                     студент не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

·                     при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

 Отметка «2» ставится в следующих случаях:

·                     не раскрыто основное содержание учебного материала;

·                     обнаружено незнание учеником большей или наиболее важной части учебного материала;

·                     допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

 

3. Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

-незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов  

обозначений величин, единиц их измерения;

-незнание наименований единиц измерения;

-неумение выделить в ответе главное;

-неумение применять знания, алгоритмы для решения задач;

-неумение делать выводы и обобщения;

-неумение читать и строить графики;

-неумение пользоваться первоисточниками, учебником и справочниками;

-потеря корня или сохранение постороннего корня;

-отбрасывание без объяснений одного из них;

-равнозначные им ошибки;

-вычислительные ошибки, если они не являются опиской;

- логические ошибки.

  К негрубым ошибкам следует отнести:

-неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

-неточность графика;

-нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

-нерациональные методы работы со справочной и другой литературой;

-неумение решать задачи, выполнять задания в общем виде.

  Недочетами являются:

-нерациональные приемы вычислений и преобразований;

-небрежное выполнение записей, чертежей, схем, графиков.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ            

 

 

Основные источники:

1.     В. П. Григорьев, Ю. А. Дубинский. Элементы высшей математики – М., 2016 г.

2.     С. Г. Григорьев, С. В. Задулина. Математика – М., 2017 г.

Дополнительные источники:

1        Яковлев Г.Н. Алгебра и начала анализа (Математика для техникумов) [Электронный учебник] /Г.Н Яковлев. - Режим доступа: http://lib.mexmat.ru/books/78472/.

2        Калашникова В.А. Методическое пособие: «Конспекты лекций по математике» [Электронный ресурс] /В.А. Калашникова. - Режим доступа: http://www.exponenta.ru/educat/systemat/kalashnikova/inde/.

3        Курош А.Г. Курс высшей алгебры [Электронный учебник] /А.Г. Курош. - Режим доступа: http://www.gaudeamus.omskcity.com/PDF_library_natural-science_8.html/

4        Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия [Электронный учебник] /А.И. Кострикин. - Режим доступа: http://www.gaudeamus.omskcity.com/PDF_library_natural-science_8.html/

 

 

 

 

 

 

 

Скачано с www.znanio.ru