
Министерство образования Саратовской области
Новобурасский филиал
Государственное автономное профессиональное образовательное учреждение
Саратовской области
«БАЗАРНОКАРАБУЛАКСКИЙ ТЕХНИКУМ АГРОБИЗНЕСА»
|
УТВЕРЖДАЮ Зав. филиалом ГАПОУ СО «БТА» _____________ /Бочкарёва Т.П../ «___»________________20____г.
|
Комплект
контрольно–оценочных средств
по учебной дисциплине
ОУД.04 Математика
по программе подготовки квалифицированных рабочих, служащих для профессии
35. 01. 13 «Тракторист – машинист с/х производства»
на базе основного общего образования с получением среднего общего образования
2019
Комплект контрольно-оценочных средств разработан на основе Федерального государственного образовательного стандарта среднего профессионального образования по профессии 35. 01. 13 «Тракторист – машинист с/х производства» по учебной дисциплине ОУД.04 Математика
Уровень подготовки базовый
Организация-разработчик: Новобурасский филиал Государственное автономное профессиональное образовательное учреждение Саратовской области «Базарнокарабулакский техникум агробизнеса»
Разработчик Захарова Н.М.- преподаватель ГАПОУ СО «БТА»
|
Одобрено на заседании комиссии общеобразовательных дисциплин Протокол № ___от «____ » _________20___ г. Председатель ___________ / Шалакова О.В./
|
|
Одобрено методическим советом Протокол № ___ от «____»____________20___ г. Председатель ___________ /Шалакова О.В./
|
СОДЕРЖАНИЕ
1. Паспорт комплекта контрольно-оценочных средств
2. Результаты освоения учебной дисциплины, подлежащие проверке
3. Оценка освоения учебной дисциплины
3.1. Формы и методы оценивания
3.2. Типовые задания для оценки освоения учебной дисциплины
4. Контрольно-оценочные материалы для промежуточной аттестации
1. Паспорт комплекта контрольно-оценочных средств
В результате освоения учебной дисциплины ОУД.04.Математика
обучающийся должен обладать предусмотренными ФГОС по профессии
35. 01. 13 «Тракторист – машинист с/х производства»
базового уровня подготовки следующими умениями, знаниями, которые
формируют профессиональную компетенцию, и общими компетенциями:
![]() выполнять
арифметические действия над числами, сочетая устные и письменные приемы;
находить приближенные значения величин и погрешности вычислений; сравнивать
числовые выражения; применять теорию при
решении задач на действия с векторами
выполнять
арифметические действия над числами, сочетая устные и письменные приемы;
находить приближенные значения величин и погрешности вычислений; сравнивать
числовые выражения; применять теорию при
решении задач на действия с векторами
![]() находить
значения корня, степени, логарифма, тригонометрических выражений на основе
определения, используя при необходимости инструментальные средства;
пользоваться приближенной оценкой при практических расчетах;
находить
значения корня, степени, логарифма, тригонометрических выражений на основе
определения, используя при необходимости инструментальные средства;
пользоваться приближенной оценкой при практических расчетах;
![]() выполнять
преобразования выражений, применяя формулы, связанные со свойствами степеней,
логарифмов, тригонометрических функций;
выполнять
преобразования выражений, применяя формулы, связанные со свойствами степеней,
логарифмов, тригонометрических функций;
![]() вычислять
значение функции по заданному значению аргумента при различных способах задания
функции; строить графики функций, иллюстрировать по графику свойства
элементарных функций;
вычислять
значение функции по заданному значению аргумента при различных способах задания
функции; строить графики функций, иллюстрировать по графику свойства
элементарных функций;
![]() находить
производные элементарных функций;
находить
производные элементарных функций;
![]() использовать
производную для изучения свойств функций и построения графиков;
использовать
производную для изучения свойств функций и построения графиков;
![]() применять
производную для проведения приближенных вычислений, решать задачи прикладного
характера на нахождение наибольшего и наименьшего значения;
применять
производную для проведения приближенных вычислений, решать задачи прикладного
характера на нахождение наибольшего и наименьшего значения;
![]() вычислять
в простейших случаях площади и объемы с использованием определенного интеграла;
вычислять
в простейших случаях площади и объемы с использованием определенного интеграла;
![]() решать
рациональные, показательные, логарифмические, тригонометрические уравнения,
сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;
использовать графический метод решения уравнений и неравенств;
решать
рациональные, показательные, логарифмические, тригонометрические уравнения,
сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;
использовать графический метод решения уравнений и неравенств;
![]() составлять
и решать уравнения и неравенства, связывающие неизвестные величины в текстовых
(в том числе прикладных) задачах.
составлять
и решать уравнения и неравенства, связывающие неизвестные величины в текстовых
(в том числе прикладных) задачах.
![]() решать
простейшие комбинаторные задачи методом перебора, а также с использованием
известных формул;
решать
простейшие комбинаторные задачи методом перебора, а также с использованием
известных формул;
![]() вычислять
в простейших случаях вероятности событий;
вычислять
в простейших случаях вероятности событий;
![]() распознавать
на чертежах и моделях пространственные формы; соотносить трехмерные объекты с
их описаниями, изображениями;
распознавать
на чертежах и моделях пространственные формы; соотносить трехмерные объекты с
их описаниями, изображениями;
![]() описывать
взаимное расположение прямых и плоскостей в пространстве, аргументировать свои
суждения об этом расположении; анализировать в простейших случаях взаимное
расположение объектов в пространстве;
описывать
взаимное расположение прямых и плоскостей в пространстве, аргументировать свои
суждения об этом расположении; анализировать в простейших случаях взаимное
расположение объектов в пространстве;
![]() изображать
основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
изображать
основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
![]() решать
планиметрические и простейшие стереометрические задачи на нахождение
геометрических величин (длин, углов, площадей, объемов);
решать
планиметрические и простейшие стереометрические задачи на нахождение
геометрических величин (длин, углов, площадей, объемов);
![]() Основные математические термины, определения, аксиомы
и следствия из них, теоремы, формулы; свойства корней, степеней и логарифмов;
Основные математические термины, определения, аксиомы
и следствия из них, теоремы, формулы; свойства корней, степеней и логарифмов;
![]() Способы решений
рациональных, показательных, логарифмических, тригонометрических
уравнений и неравенств и их систем;
Способы решений
рациональных, показательных, логарифмических, тригонометрических
уравнений и неравенств и их систем;
![]() Элементарные функции и способы задания функций, свойства функций; построение и
преобразования графиков функций;
Элементарные функции и способы задания функций, свойства функций; построение и
преобразования графиков функций;
![]() Геометрический
и механический смысл производной;
Геометрический
и механический смысл производной;![]() равила
дифференцирования функций;
равила
дифференцирования функций;
![]() построение
графиков функций с помощью производной;
построение
графиков функций с помощью производной;
![]() Правило
нахождения наибольшего и наименьшего значений функции на отрезке; п
Правило
нахождения наибольшего и наименьшего значений функции на отрезке; п![]() производной
для решения прикладных задач;
производной
для решения прикладных задач;
![]() Свойства
и способы вычисления неопределённого и определённого интегралов;
Свойства
и способы вычисления неопределённого и определённого интегралов;![]() правила
интегрирования функций;
правила
интегрирования функций;
![]() определённого
интеграла для решения прикладных задач;
определённого
интеграла для решения прикладных задач;
![]() действия
над векторами;
действия
над векторами;![]() векторов
для решения прикладных задач;
векторов
для решения прикладных задач;
![]() Взаимное
расположение прямых, прямой и плоскости, двух плоскостей в пространстве;
Взаимное
расположение прямых, прямой и плоскости, двух плоскостей в пространстве;
![]() Элементы комбинаторики.
Элементы комбинаторики.
![]() Элементы теории вероятности и
математической статистики
Элементы теории вероятности и
математической статистики
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, исходя из цели и способов ее достижения, определенных руководителем.
ОК 3 Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.
ОК 4 Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач.
ОК5 Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6 Работать в команде, эффективно общаться с коллегами, руководством, клиентами.
ОК 7 Организовать собственную деятельность с соблюдением требований охраны труда и экологической безопасности.
ОК 8 Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей)
Формой аттестации по учебной дисциплине является экзамен
2. Результаты освоения учебной дисциплины, подлежащие проверке
2.1. В результате аттестации по учебной дисциплине осуществляется
комплексная проверка следующих умений и знаний, а также динамика
формирования общих компетенций:
Таблица 1.1
|
Результаты обучения: умения, знания и общие компетенции |
Показатели оценки результата |
Форма контроля и оценивания |
|
Уметь: |
|
|
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное выполнение арифметических действий над числами, нахождение приближенных значений величин и погрешности вычислений; сравнение числовых выражений; выполнение действий с векторами |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное нахождение значений корня, степени, логарифма, тригонометрических выражений; использование приближенной оценки при практических расчетах |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
|
верное выполнение преобразо-ваний выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное вычисление значений функции по заданному значению аргумента при различных способах задания функции; построение графиков функций, иллюстрирование по графику свойств элементарных функций; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4.
|
верное нахождение производных элементарных функций |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное использование производной для изучения свойств функций и построения графиков; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное применение производной для проведения приближенных вычислений, решение задач прикладного характера на нахождение наибольшего и наименьшего значения |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное вычисление в простейших случаях площади и объема с использованием определенного интеграла; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное решение рациональных, показательных, логарифмических, тригонометрических уравнений, сводящиеся к линейным и квадратным, а также аналогичных неравенств и систем; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное решение простейших комбинаторных задач методом перебора, а также с использованием известных формул; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное вычисление в простейших случаях вероятности событий
|
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное распознавание на чертежах и моделях пространственных форм; соотнесение трехмерных объектов с их описаниями, изображениями; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное описывание взаимного расположения прямых и плоскостей в пространстве, аргументирование своих суждений об этом расположении; анализ в простейших случаях взаимного расположения объектов в пространстве; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное изображение основных многогранников и круглых тел; выполнение чертежей по условиям задач; построение простейших сечений куба, призмы, пирамиды; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
верное решение планиметрических и простейших стереометрических задач на нахождение геометрических величин (длин, углов, площадей, объемов); |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
Знать: |
|
|
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание основных математических терминов, определений, аксиом и следствий из них, теорем, формул; свойств корней, степеней и логарифмов; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание способов решений рациональных, показательных, логарифмических, тригонометрических уравнений и неравенств и их систем; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание элементарных функций и способов задания функций, свойств функций; построение и преобразова-ния графиков функций |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание геометрического и
механического смысла производной; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание методики исследования функции и построения графиков функций с помощью производной |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание правил нахождения наибольшего
и наименьшего значений функции на отрезке; п |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание свойств и способов вычисления неопределённого и определённого интегралов; правил интегрирования функций |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание правил применения определённого интеграла для решения прикладных задач;
|
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
Знание правил действий над
векторами;
|
устный опрос, тестирование, самостоятельная работа, экзамен |
|
ОК 1, ОК 2, ОК 3, ОК 4. |
знание взаимного расположения прямых, прямой и плоскости, двух плоскостей в пространстве; |
устный опрос, тестирование, самостоятельная работа, экзамен |
|
|
Знание элементов комбинаторики |
устный опрос, тестирование, самостоятельная работа |
|
|
Знание элементов теории вероятности и математической статистики |
устный опрос, тестирование, самостоятельная работа |
3. Оценка освоения учебной дисциплины:
3.1. Формы и методы оценивания
Предметом оценки служат умения и знания, предусмотренные ФГОС по дисциплине ОУД.04 Математика, направленные на формирование общих и профессиональных компетенций.
|
Контроль и оценка освоения учебной дисциплины по темам (разделам) Таблица 2.2 |
||||||
|
Элемент учебной дисциплины
|
Формы и методы контроля |
|||||
|
Текущий контроль |
Рубежный контроль |
Промежуточная аттестация |
||||
|
Форма контроля |
Проверяемые ОК, У, З |
Форма контроля |
Проверяемые ОК, У, З |
Форма контроля |
Проверяемые ОК, У, З |
|
|
Раздел 1 |
|
|
Контрольная работа № 1 |
|
экзамен |
ОК 4. |
|
Тема 1.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 1.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 2 |
|
|
Контрольная работа № 2 |
ОК3, ОК 4. |
экзамен |
|
|
Тема 2.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 2.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 3 |
|
|
Контрольные работы № 3, № 4 |
|
экзамен |
|
|
Тема 3.1 |
Устный опрос Самостоятельная работа Тестирование |
|
|
|
|
|
|
Тема 3.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 3.3 |
Устный опрос Самостоятельная работа Тестирование |
|
|
|
|
|
|
Раздел 4 |
|
|
Контрольная работа № 5 |
|
экзамен |
|
|
Тема 4.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 4.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 5 |
|
|
Контрольная работа № 6 |
|
экзамен |
|
|
Тема 5.1 |
Устный опрос Самостоятельная работа Тестирование |
|
|
|
|
|
|
Тема 5.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 5.3 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 6 |
|
|
Контрольная работа № 7 |
|
экзамен |
|
|
Тема 6.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 6.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 6.3 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 7 |
|
|
Контрольная работа № 8 |
ОК 4. |
экзамен |
|
|
Тема 7.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 7.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 8 |
|
|
Контрольная работа № 9 |
|
экзамен |
|
|
Тема 8.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 8.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 8.3 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 8.4 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 9 |
|
|
Контрольная работа № 10 |
|
экзамен |
|
|
Тема 9.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 9.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 9.3 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 10 |
|
|
Контрольная работа № 11 |
|
экзамен |
|
|
Тема 10.1 |
Устный опрос Самостоятельная работа Тестирование |
|
|
|
|
|
|
Раздел 11 |
|
|
Самостоятельная работа Контрольная работа № 12 |
|
экзамен |
|
|
Тема 11.1 |
Устный опрос Самостоятельная работа Тестирование |
|
|
|
|
|
|
Тема 11.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Раздел 12 |
|
|
Контрольная работа № 13 |
ОК3, ОК 4. |
экзамен |
|
|
Тема 12.1 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.2 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.3 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.4 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.5 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.6 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.7 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
|
Тема 12.8 |
Устный опрос Самостоятельная работа |
|
|
|
|
|
3.2. Типовые задания для оценки освоения учебной дисциплины
3.2.1. Текущий контроль по теме «Развитие понятия о числе»
Типовые задания для оценки знаний ![]() , умений
, умений ![]()
Контрольная работа № 1
Вариант 1.
1.Обратите
обыкновенную дробь ![]() в десятичную периодическую.
в десятичную периодическую.
2. Найдите абсолютную погрешность округления до единиц числа 0,8.
3.Выполните сложение комплексных чисел:
![]() =
- 3 +5i ,
=
- 3 +5i , ![]() =
4 -7i
=
4 -7i
4.Найдите разность комплексных чисел:
![]() =
2 - 4i ,
=
2 - 4i , ![]() =
5 + 6i
=
5 + 6i
5.Выполните умножение комплексных чисел:
![]() =
- 1 - 3i ,
=
- 1 - 3i , ![]() =
3 - i
=
3 - i
Вариант 2.
1.Обратите
обыкновенную дробь ![]() в десятичную периодическую.
в десятичную периодическую.
2.Найдите абсолютную погрешность округления до единиц числа 7,6.
3.Выполните сложение комплексных чисел:
![]() =
- 2 +3i ,
=
- 2 +3i , ![]() =
8 -i
=
8 -i
4.Найдите разность комплексных чисел:
![]() =
1 - 2i ,
=
1 - 2i , ![]() =
-3 + 4i
=
-3 + 4i
5.Выполните умножение комплексных чисел:
![]() =
-4 - 8i ,
=
-4 - 8i , ![]() =
2 +5 i
=
2 +5 i
3.2.2. Текущий контроль по теме «Корни, степени, логарифмы»
Типовые задания для оценки знаний ![]() , умений
, умений ![]()
Контрольная работа № 2
Вариант 1.
1.Запишите
в виде степени числа 2 следующие числа: ![]()
2.Замените степени с дробными показателями корнями.
![]()
![]()
![]()
![]()
![]()
3.Замените корни степенями с дробными показателями.
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
4. Вычислите.
![]()
5. Расположить в порядке возрастания:
![]() ,
, ![]()
![]() ,
, ![]() .
.
Вариант 2.
1.Запишите
в виде степени числа 3 следующие числа: ![]()
2.Замените степени с дробными показателями корнями.
![]()
![]()
![]()
![]()
![]()
3.Замените корни степенями с дробными показателями.
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
4. Вычислите.
![]()
5.Расположить в порядке возрастания:
![]()
![]()
![]() ,
, ![]()
Тест
Вариант I
|
№ задания |
задание |
варианты ответов |
||
|
А |
В |
С |
||
|
1 |
Вычислить
|
-4 |
-3 |
-2 |
|
2 |
Вычислить
|
-1 |
-2 |
-3 |
|
3 |
Вычислить
|
-9 |
-4 |
-2 |
|
4 |
Вычислить
|
-4 |
-3 |
-2 |
|
5 |
Вычислить
|
-4 |
-3 |
-2 |
Ключ к тесту: С А С А В
Вариант II
|
№ задания |
задание |
варианты ответов |
||
|
А |
В |
С |
||
|
1 |
Вычислить
|
-4 |
-3 |
-2 |
|
2 |
Вычислить
|
-4 |
-2 |
-1 |
|
3 |
Вычислить
|
-9 |
-4 |
-2 |
|
4 |
Вычислить
|
-4 |
-3 |
-2 |
|
5 |
Вычислить
|
-4 |
-3 |
-2 |
Ключ к тесту: В С С В А
3.2.3. Текущий контроль по теме «Показательные уравнения и неравенства»
Типовые задания для оценки знаний ![]()
![]() ,
умений
,
умений ![]()
Контрольная работа № 3
1 вариант
1.Решить показательные уравнения:
1)
![]()
2)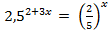
3)
![]()
2. Решить показательные неравенства:
1)
![]()
![]()
2)
![]()
2 вариант
1.Решить показательные уравнения:
1)
![]()
2)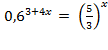
3)
![]()
2. Решить показательные неравенства:
1)
![]() 0,8
0,8
2)
![]()
3.2.4. Текущий контроль по теме «Логарифмические уравнения и неравенства»
Типовые задания для оценки знаний ![]()
![]() , умений
, умений ![]()
Контрольная работа № 4
1 вариант
1.Решить логарифмические уравнения:
![]()
2)![]()
![]() (3x - 1) = - 3
(3x - 1) = - 3
2.Решить логарифмические неравенства:
![]()
![]()
2 вариант
1.Решить логарифмические уравнения:
1)
![]()
2) ![]()
![]() (2x – 1) = - 2
(2x – 1) = - 2
2.Решить логарифмические неравенства:
1)
![]()
![]()
Тест
Вариант I
|
№ задания |
задание |
варианты ответов |
||
|
А |
В |
С |
||
|
1 |
Решить уравнение
|
0 |
1 |
2 |
|
2 |
Решить уравнение
|
6 |
7 |
8 |
|
3 |
Решить уравнение
|
6 |
7 |
8 |
|
4 |
Решить уравнение
|
0 |
1 |
2 |
|
5 |
Решить уравнение
|
3
|
2 |
1 |
Ключ к тесту: А В С С А
Вариант 2
|
№ задания |
задание |
варианты ответов |
||
|
А |
В |
С |
||
|
1 |
Решить уравнение
|
1 |
2 |
3 |
|
2 |
Решить уравнение
|
4 |
5 |
6 |
|
3 |
Решить уравнение
|
9 |
10 |
11 |
|
4 |
Решить уравнение
|
6 |
7 |
8 |
|
5 |
Решить уравнение
|
1
|
2 |
3 |
Ключ к тесту: С С В А В
3.2.5. Текущий контроль по теме «Прямые и плоскости в пространстве»
Типовые задания для оценки знаний![]()
![]() умений
умений
![]()
Контрольная работа № 5
Вариант 1
1. Треугольники АВС и АВД не лежат в одной плоскости. Докажите, что любая прямая, параллельная отрезку СД, пересекает плоскости данных треугольников.
2. Точка С лежит на отрезке АВ, причём АВ : ВС = 4 : 3. Отрезок СД, равный 12 см, параллелен плоскости α , проходящей через точку В. Докажите , что прямая АД пересекает плоскость α в некоторой точке М. Найдите отрезок ВМ.
3.
Изобразите параллелепипед АВСД![]() и
постройте его сечение плоскостью, проходящей через точки
и
постройте его сечение плоскостью, проходящей через точки![]() и
середину ребра СД .
и
середину ребра СД .
4.Отрезок АД перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ = АС = 5 см, ВС = 6 см, АД = 12 см.Найдите расстояния от концов отрезка АД до прямой ВС.
5. Ребро СД тетраэдра АВСД перпендикулярно к плоскости АВС,
АВ
= ВС = АС = 6 см. ВД = 3![]() ДАСВ,
ВДСА.
ДАСВ,
ВДСА.
Вариант 2
1.Точки А и В лежат в плоскости α , а точка С не лежит в этой плоскости. Докажите, что прямая , проходящая через середины отрезков АС и ВС, параллельна плоскости α.
2.В трапеции АВСД основание ВС = 12 см. Точка М не лежит в плоскости трапеции, а точка К – середина отрезка ВМ. Докажите, что плоскость АДК пересекает отрезок МС в некоторой точке Р. Найдите отрезок КР.
3.
Изобразите параллелепипед АВСД![]() и постройте его сечение плоскостью ВКМ, где точка К – середина ребра А
и постройте его сечение плоскостью ВКМ, где точка К – середина ребра А![]() .
.
4.Через вершину А прямоугольника АВСД проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что КД = 6 см, КВ = 7 см, КС = 9 см. Найдите расстояние от точки К до плоскости прямоугольника АВСД, площадь прямоугольника АВСД.
5. Ребро СД тетраэдра АВСД перпендикулярно к плоскости АВС,
АВ
= ВС = АС = 6 см. ВД = 3![]() ДАВС.
ДАВС.
3.2.6. Текущий контроль по теме «Основы тригонометрии »
Типовые задания для оценки знаний ![]() умений
умений
![]() ,
, ![]()
Контрольная работа № 6
Вариант 1
1.Найти множество значений функции: y = 3 sin x+ 2
2.
Найти tg x,
если sin x
= - ![]() ,
, ![]() .
.
3. Решить уравнения:
1)
4 cos ( 2x + ![]() ) + 2 = 0
) + 2 = 0
2)
2 sin ( 3x - ![]() ) –
) – ![]()
3) 3![]() - 2 = 0
- 2 = 0
Вариант 2
1.Найти множество значений функции: y = 2 cos x - 3
2.
Найти tg x,
если cos x
= - ![]() ,
, ![]() .
.
3. Решить уравнения:
1)
2 cos ( 3x + ![]() ) –
) – ![]() 0
0
2)
2 sin ( 2x + ![]() ) + 1
) + 1 ![]()
3) ![]() - 3 = 0
- 3 = 0
3.2.7. Текущий контроль по теме «Многогранники»
Типовые задания для оценки знаний ![]()
![]() умений
умений
![]()
Контрольная работа № 7
Вариант 1
1. Периметр основания прямоугольного параллелепипеда=16см. Длина на 2см больше ширины, а высота равна разности длины и ширины. Найти объём параллелепипеда.
2. Основание пирамиды- ромб, сторона которого равна 5 см, а одна из диагоналей = 8 см. Найдите боковые рёбра пирамиды, если высота пирамиды проходит через точку пересечения диагоналей и равна 7 см.
3. Основанием прямого параллелепипеда является ромб с диагоналями 10 см
и 24 см, а высота параллелепипеда равна 10 см. Найдите большую диагональ
параллелепипеда.
4. Основанием пирамиды является квадрат, одно из
боковых рёбер перпендикулярно к плоскости основания. Плоскость боковой грани,
не проходящей через высоту пирамиды, наклонена к плоскости основания под
углом ![]() . Наибольшее боковое ребро равно 12 см.Найдите высоту
пирамиды.
. Наибольшее боковое ребро равно 12 см.Найдите высоту
пирамиды.
5. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Вариант 2
1. Площадь основания прямоугольного параллелепипеда =20 см2. Длина на 1см больше ширины, а высота равна сумме длины и ширины. Найти объём параллелепипеда.
2. Диагональ правильной четырёхугольной призмы наклонена
к плоскости основания под углом ![]() .найдите площадь сечения, проходящего через сторону
нижнего основания и противолежащую сторону верхнего основания, если диагональ
основания равна 4
.найдите площадь сечения, проходящего через сторону
нижнего основания и противолежащую сторону верхнего основания, если диагональ
основания равна 4![]() см.
см.
3. Основание пирамиды – квадрат площадью 25 см2. Высота проходит через точку пересечения диагоналей и равна 5 см. Найдите боковое ребро пирамиды.
4. Через два противолежащих ребра куба проведено сечение,
площадь которого равна 64![]()
![]() . Найдите ребро куба и его диагональ.
. Найдите ребро куба и его диагональ.
5. Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведённая из вершины пирамиды, равна 41 см. Найдите площадь основания пирамиды, если его периметр равен 42 см.
3.2.8. Текущий контроль по теме «Координаты и векторы»
Типовые задания для оценки знаний![]()
![]() умений
умений
![]()
Контрольная работа № 8
Вариант 1
1. Найдите координаты вектора АВ, если: А(3;-1;2), В(2;-1;4)
2. Определите вид треугольника АВС, если А(9;3;-5), В(2;10;-5), С(2;3;2).
3. Даны векторы а{3;-2;1} и b{-2;3;1. Найдите |a+b|
4. Вычислите угол между прямыми AB и CD, если A(3;-2;4), B(4;-1;2), C(6;-3;2),
D(7;-3;1).
5. Вычислите косинус угла между прямыми AB и CD, если даны координаты точек
A(7;-8;15), B(8;-7;13), C(2;-3;5), D(-1;0;4).
Вариант 2
1. Найдите координаты вектора АВ, если: А(-2;6;-2), В(3;-1;0)
2. Определите вид треугольника АВС, если А(3;7;-4), В(5;-3;2), С(1;3;-10).
3. Даны векторы а{3;-2;1} и b{-2;3;1}. Найдите |a| + |b|
4. Вычислите угол между прямыми AB и CD, если A(5;-8;-1), B(6;-8;-2), C(7;-5;-11),
D(7;-7;-9).
5. Вычислите косинус угла между прямыми AB и CD, если даны координаты точек
A(8;-2;3), B(3;-1;4), C(5;-2;0), D(7;0;-2).
3.2.9. Текущий контроль по теме «Начала анализа»
Типовые задания для оценки знаний ![]()
![]()
![]()
![]() умений
умений ![]()
Контрольная работа № 9
Вариант 1
1).Найти производную функции в данной точке:
f(х)
= 3 х + ![]() ,
, ![]()
2).Написать уравнение касательной, проведённой к графику данной функции
в
данной точке: f( х ) = ![]() + 7х – 16,
+ 7х – 16, ![]()
3). Найти точки экстремума
функции: f( х ) = ![]() + 4
+ 4
4).Найти первообразную функции, проходящую через точку М:
f( х
) = ![]() + 5, М ( 3; 28
)
+ 5, М ( 3; 28
)
5).Вычислить площадь фигуры, ограниченной осями координат, параболой и прямой:
f( х
) = ![]() - 6х + 9, х
- 6х + 9, х ![]()
Вариант 2
1).Найти производную функции в данной точке:
f(х) = 4sin х – cos х, ![]()
2).Написать уравнение касательной, проведённой к графику данной функции
в
данной точке: f( х ) = ![]() + 3х – 2,
+ 3х – 2, ![]()
3). Найти точки экстремума
функции: f( х ) = ![]()
4).Найти первообразную функции, проходящую через точку М:
f( х
) = 6 ![]() + 2, М ( 2 ; 25 )
+ 2, М ( 2 ; 25 )
5).Вычислить площадь фигуры, ограниченной осями координат, параболой и прямой:
f( х
) = ![]() + 8х + 16, х
+ 8х + 16, х ![]()
3.2.10. Текущий контроль по теме «Тела и поверхности тел вращения»
Типовые задания для оценки знаний ![]() умений
умений
![]()
Контрольная работа № 10
Вариант 1
1. Найдите диагональ осевого сечения цилиндра. Если его радиус равен 1,5 м. а высота равна 4 м.
2. Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см. Найдите высоту и площадь основания цилиндра.
3. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3 см.
4.
Найдите высоту конуса, если
площадь его осевого сечения равна 6![]() . а площадь основания равна 8
. а площадь основания равна 8![]() .
.
5. Найдите площадь сферы, радиус которой равен ![]() м.
м.
Вариант 2
1. Диагональ осевого сечения цилиндра равна 48 см. Угол
между этой диагональю и образующей цилиндра равен ![]()
2. Высота цилиндра равна 10 дм. Площадь сечения цилиндра
плоскостью, параллельной оси цилиндра и удалённой на 9 дм от неё, равна 240![]()
![]()
3. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.
4. Найдите угол при вершине осевого сечения конуса, если
развёрткой его боковой поверхности является сектор с дугой, равной ![]()
5. Найдите площадь сферы, радиус которой равен ![]() м.
м.
3.2.11. Текущий контроль по теме «Измерения в геометрии»
Типовые задания для оценки знаний ![]() , умений
, умений ![]()
Контрольная работа № 11
Вариант 1
1. Объём конуса =48π см3.Радиус основания=4 см. Найти высоту конуса.
2. Радиус шара = 4 см. Найдите объём шара и площадь его поверхности.
3. Объём цилиндра = 8 π см3, а высота равна радиусу. Найдите высоту цилиндра.
4. Периметр основания прямоугольного параллелепипеда=16см. Длина на 2см больше ширины, а высота равна разности длины и ширины. Найти объём
5. Основание пирамиды- ромб, сторона которого равна 5 см, а одна из диагоналей = 8 см. Найдите боковые рёбра пирамиды, если высота пирамиды проходит через точку пересечения диагоналей и равна 7 см.
Вариант 2
1. Найти объём конуса, если его высота =3 см, а радиус основания =1,5 см.
2. Площадь поверхности шара = 64 π см2.Найдите радиус и объём шара.
3. Объём цилиндра = 120 π см3. , а высота равна 3,6 см. Найдите радиус цилиндра.
4. Площадь основания прямоугольного параллелепипеда =20 см2. Длина на 1см больше ширины, а высота равна сумме длины и ширины. Найти объём параллелепипеда.
5. Основание пирамиды – квадрат площадью 25 см2. Высота проходит через точку пересечения диагоналей и равна 5 см. Найдите боковое ребро пирамиды.
3.2.12. Текущий контроль по теме «Элементы комбинаторики»
Типовые задания для оценки знаний ![]() , умений
, умений ![]()
Самостоятельная работа
Вариант 1
1. Сколькими способами можно рассадить за столом 6 человек?
2. Сколькими способами можно украсить костюм, пришив четырехцветные
полоски из лент, имея 7 лент различных цветов?
3. Сколькими способами можно составить набор из двух бракованных деталей и трёх качественных, если есть 20 деталей, из которых 8 бракованных?
4. Сколькими способами можно взять 2 чёрных и 3 белых шара, если есть 12
белых и 10 чёрных шаров?
5. Сколькими способами можно разложить 8 разных открыток в 8 разных конвертов, если в каждый конверт кладётся только одна открытка?
Вариант 2
1. Сколькими способами можно расставить на одной полке 5 книг?
2. Сколькими способами можно выбрать четырёх лиц на 4 различные должности из 9 кандидатов?
3. Сколькими способами можно составить дозор из трёх солдат и одного офицера , если есть 50 солдат и 3 офицера ?
4. Сколькими способами можно взять 3 чёрных и 2 белых шара , если есть
8 белых и 12 чёрных шаров?
5. Каким числом способов можно разложить 4 разные монеты в 4 кармана так, чтобы в каждом кармане оказалась ровно одна монета?
3.2.13. Текущий контроль по теме «Элементы теории вероятности »
Типовые задания для оценки знаний ![]() ,
, ![]() , умений
, умений ![]()
Контрольная работа № 12
Вариант 1
1. В магазин привезли 28 телевизоров, среди которых 5 телевизоров имеют скрытые дефекты. Какова вероятность того, что первые два покупателя купят телевизоры купят телевизоры без дефектов?
2. В коробке находятся 20 белых и 15 чёрных шаров. Наудачу вынимают один шар и он оказывается белым. Какова вероятность того, что следующий шар тоже окажется белым?
3. В партии из 20 деталей 8 бракованных. Контролёр берёт 5 деталей. Какова вероятность того, что хотя бы одна из них окажется бракованной?
4. В коробке 5 белых и 7 чёрных шаров. Какова вероятность, что два наудачу вынутых шара окажутся белыми?
5. Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо 4 и 5 одновременно?
Вариант 2
1. В магазин привезли 30 телевизоров, среди которых 6 телевизоров имеют скрытые дефекты. Какова вероятность того, что первые два покупателя купят телевизоры без дефектов?
2. В коробке находятся 18 белых и 12 чёрных шаров. Наудачу вынимают один шар и он оказывается белым. Какова вероятность того, что следующий шар окажется чёрным?
3. В партии из 24 деталей 7 бракованных. Контролёр берёт 5 деталей. Какова вероятность того, что хотя бы одна из них окажется бракованной?
4. В коробке 8 белых и 10 чёрных шаров. Какова вероятность, что два наудачу вынутых шара окажутся чёрными?
5. Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 3, либо 5, либо 3 и 5 одновременно?
3.2.14. Текущий контроль по теме «Уравнения и неравенства»
Типовые задания для оценки знаний ![]()
![]() умений
умений
![]()
Контрольная работа № 13
Вариант 1
1. Решите уравнения:
1) ![]() +
+
![]()
2) ![]() =
= ![]()
3) ![]()
2. Решите неравенства:
![]()
2) ![]()
![]()
Вариант 2
1. Решите уравнения:
1)
![]() +
+
![]()
2) ![]() = 2
= 2![]()
3) ![]() =
= ![]()
2. Решите неравенства:
![]()
2) ![]()
![]()
4. Контрольно-оценочные материалы для промежуточной аттестации по учебной дисциплине
Назначение:
КИМ предназначен для контроля и оценки результатов освоения учебной
дисциплины ОУД.04 Математика по профессии 35. 01. 13 «Тракторист – машинист с/х производства»
Умения
![]() выполнять арифметические действия над числами, сочетая
устные и письменные приемы; находить приближенные значения величин и
погрешности вычислений; сравнивать числовые выражения; применять теорию при решении задач на действия с векторами
выполнять арифметические действия над числами, сочетая
устные и письменные приемы; находить приближенные значения величин и
погрешности вычислений; сравнивать числовые выражения; применять теорию при решении задач на действия с векторами
![]() находить значения корня, степени, логарифма,
тригонометрических выражений на основе определения, используя при необходимости
инструментальные средства; пользоваться приближенной оценкой при практических
расчетах;
находить значения корня, степени, логарифма,
тригонометрических выражений на основе определения, используя при необходимости
инструментальные средства; пользоваться приближенной оценкой при практических
расчетах;
![]() выполнять преобразования выражений, применяя формулы,
связанные со свойствами степеней, логарифмов, тригонометрических функций;
выполнять преобразования выражений, применяя формулы,
связанные со свойствами степеней, логарифмов, тригонометрических функций;
![]() вычислять значение функции по заданному значению
аргумента при различных способах задания функции; строить графики функций,
иллюстрировать по графику свойства элементарных функций;
вычислять значение функции по заданному значению
аргумента при различных способах задания функции; строить графики функций,
иллюстрировать по графику свойства элементарных функций;
![]() находить производные элементарных функций;
находить производные элементарных функций;
![]() использовать производную для изучения свойств функций и
построения графиков;
использовать производную для изучения свойств функций и
построения графиков;
![]() применять производную для проведения приближенных
вычислений, решать задачи прикладного характера на нахождение наибольшего и
наименьшего значения;
применять производную для проведения приближенных
вычислений, решать задачи прикладного характера на нахождение наибольшего и
наименьшего значения;
![]() вычислять в простейших случаях площади и объемы с
использованием определенного интеграла;
вычислять в простейших случаях площади и объемы с
использованием определенного интеграла;
![]() решать рациональные, показательные, логарифмические,
тригонометрические уравнения, сводящиеся к линейным и квадратным, а также
аналогичные неравенства и системы; использовать графический метод решения
уравнений и неравенств;
решать рациональные, показательные, логарифмические,
тригонометрические уравнения, сводящиеся к линейным и квадратным, а также
аналогичные неравенства и системы; использовать графический метод решения
уравнений и неравенств;
![]() составлять и решать уравнения и неравенства, связывающие
неизвестные величины в текстовых (в том числе прикладных) задачах.
составлять и решать уравнения и неравенства, связывающие
неизвестные величины в текстовых (в том числе прикладных) задачах.
![]() решать простейшие комбинаторные задачи методом перебора,
а также с использованием известных формул;
решать простейшие комбинаторные задачи методом перебора,
а также с использованием известных формул;
![]() вычислять в простейших случаях вероятности событий;
вычислять в простейших случаях вероятности событий;
![]() распознавать на чертежах и моделях пространственные
формы; соотносить трехмерные объекты с их описаниями, изображениями;
распознавать на чертежах и моделях пространственные
формы; соотносить трехмерные объекты с их описаниями, изображениями;
![]() описывать взаимное расположение прямых и плоскостей в
пространстве, аргументировать свои суждения об этом расположении; анализировать
в простейших случаях взаимное расположение объектов в пространстве;
описывать взаимное расположение прямых и плоскостей в
пространстве, аргументировать свои суждения об этом расположении; анализировать
в простейших случаях взаимное расположение объектов в пространстве;
![]() изображать основные многогранники и круглые тела;
выполнять чертежи по условиям задач; строить простейшие сечения куба, призмы,
пирамиды;
изображать основные многогранники и круглые тела;
выполнять чертежи по условиям задач; строить простейшие сечения куба, призмы,
пирамиды;
![]() решать планиметрические и простейшие стереометрические
задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
решать планиметрические и простейшие стереометрические
задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
Знания
![]() Основные математические термины, определения, аксиомы
и следствия из них, теоремы, формулы; свойства корней, степеней и логарифмов;
Основные математические термины, определения, аксиомы
и следствия из них, теоремы, формулы; свойства корней, степеней и логарифмов;
![]() Способы решений
рациональных, показательных, логарифмических, тригонометрических
уравнений и неравенств и их систем;
Способы решений
рациональных, показательных, логарифмических, тригонометрических
уравнений и неравенств и их систем;
![]() Элементарные функции и способы задания функций, свойства функций; построение и
преобразования графиков функций;
Элементарные функции и способы задания функций, свойства функций; построение и
преобразования графиков функций;
![]() Геометрический
и механический смысл производной;
Геометрический
и механический смысл производной;![]() равила
дифференцирования функций;
равила
дифференцирования функций;
![]() построение
графиков функций с помощью производной;
построение
графиков функций с помощью производной;
![]() Правило
нахождения наибольшего и наименьшего значений функции на отрезке; п
Правило
нахождения наибольшего и наименьшего значений функции на отрезке; п![]() производной
для решения прикладных задач;
производной
для решения прикладных задач;
![]() Свойства
и способы вычисления неопределённого и определённого интегралов;
Свойства
и способы вычисления неопределённого и определённого интегралов;![]() правила
интегрирования функций;
правила
интегрирования функций;
![]() определённого
интеграла для решения прикладных задач;
определённого
интеграла для решения прикладных задач;
![]() действия
над векторами;
действия
над векторами;![]() векторов
для решения прикладных задач;
векторов
для решения прикладных задач;
![]() Взаимное
расположение прямых, прямой и плоскости, двух плоскостей в пространстве;
Взаимное
расположение прямых, прямой и плоскости, двух плоскостей в пространстве;
![]() Элементы комбинаторики.
Элементы комбинаторики.
![]() Элементы теории вероятности и
математической статистики
Элементы теории вероятности и
математической статистики
Содержание и структура экзаменационной работы
Для проведения письменного экзамена по математике подготовлен комплект экзаменационных материалов в виде текста контрольных работ.
Контрольная работа состоит из шести заданий: показательные уравнения или неравенства, логарифмические уравнения или неравенства, тригонометрические уравнения или дробные рациональные неравенства, задача на применение производной, задача на применение первообразной, геометрическая задача на нахождение объёмов многогранников.
Краткая инструкция по выполнению экзаменационной работы
1.На экзамен обучающиеся приходят за 20 мин до начала экзамена.
2. На выполнение письменной экзаменационной работы по математике: алгебре и началам математического анализа отводится 6 астрономических часов (360 минут).
3. Работа выполняется на листах, в чистовик вносятся личные данные под руководством преподавателя. Сначала рекомендуется выполнить задание на листах для черновика.
4 Во время проведения экзаменов запрещается иметь при себе и использовать средства связи и электронно-вычислительную технику, за исключением случаев, установленных нормативно-правовыми актами РФ.
5. Чертежи следует выполнять карандашом с применением чертёжных инструментов.
6. Во время экзамена обучающиеся не вправе общаться друг с
другом, свободно перемещаться по кабинету, пользоваться справочными
материалами, иметь при себе и использовать средства связи и
электронно-вычислительной техники.
Учащиеся могут выходить из кабинета в случае необходимости, предварительно сдав
листы с работой.
7. После выполнения экзаменационная работа сдается для проверки вместе с черновиком.
Текст экзаменационной работы
Текст 1
Вариант 1
1. Решить неравенство: ![]()
2. Решить систему уравнений: ![]()
3. Решить уравнение ![]()
4. Найти интервалы убывания функции y = 2![]() – 6x
– 6x
5. Найти площадь фигуры, ограниченной
линиями ![]() ,
, ![]()
6. Высота правильной
четырёхугольной пирамиды равна 3 см. Площадь боковой поверхности равна 80 ![]() . Найти объём пирамиды.
. Найти объём пирамиды.
Вариант 2
1. Решить неравенство: ![]()
2. Решить систему уравнений ![]()
3. Решить уравнение ![]()
4. Найти интервалы возрастания функции y = 3x - ![]()
5. Найти площадь фигуры, ограниченной
линиями ![]() ,
, ![]()
6. Сторона основания правильной четырёхугольной пирамиды равна 6 см. Площадь боковой поверхности в 2 раза больше площади основания. Найти объём пирамиды.
Текст 2
Вариант 1
1. Решите уравнение ![]()
2. Решите неравенство ![]()
3. Решите уравнение sin х + sin ( π- х) – cos (![]() – х ) = - 1
– х ) = - 1
4. Дана функция f( х ) = ![]() – 12 х + 1. Найдите координаты точки
её графика, в которой угловой коэффициент касательной к нему равен 8.
– 12 х + 1. Найдите координаты точки
её графика, в которой угловой коэффициент касательной к нему равен 8.
5. Найдите площадь фигуры, ограниченной графиком функции
f( х ) = ![]() - 6х + 8, прямыми х
- 6х + 8, прямыми х ![]() , х
, х ![]() и осью абсцисс.
и осью абсцисс.
6. Диагональ меньшей боковой грани прямоугольного параллелепипеда равна большему ребру основания. Высота параллелепипеда равна 2 см, диагональ основания равна 14 см. Найдите объём параллелепипеда.
Вариант 2
1.
Решите
уравнение ![]()
2.
Решите
неравенство ![]()
3.
Решите
уравнение cos х + cos ( π + х) – sin (![]() – х ) = 0
– х ) = 0
4.
К графику
функции f( х ) = ![]() проведена касательная с угловым
коэффициентом = - 9. Найдите координаты точки касания.
проведена касательная с угловым
коэффициентом = - 9. Найдите координаты точки касания.
5. Найдите площадь фигуры, ограниченной осями координат, графиком функции
f( х
) = ![]() + 8х + 16 и прямой х
+ 8х + 16 и прямой х ![]()
6. Основание прямой призмы - прямоугольный треугольник с гипотенузой 10 см и катетом 6 см. Больший катет треугольника в основании призмы равен диагонали меньшей из боковых граней. Найдите объём призмы.
Текст 3
Вариант 1
1. Решите уравнение ![]()
2.
Решите
неравенство ![]()
3.
Вычислите sin 2х , если cos x = - ![]() , π
, π ![]()
4.
Найдите
координаты точек графика функции f(![]() ) =
) =![]() ,в которых касательная, проведённая
к графику функции, параллельна оси абсцисс.
,в которых касательная, проведённая
к графику функции, параллельна оси абсцисс.
5.
Найти площадь
фигуры, ограниченной линиями ![]() ,
, ![]()
6. Периметр боковой грани правильной четырёхугольной призмы равен 12 см.
При какой длине стороны основания призмы её объём будет наибольшим?
Вариант 2
1. Решите уравнение ![]()
2. Решите неравенство ![]()
3. Вычислите cos 2x, если sin x = - ![]() , π
, π ![]()
4. Найдите координаты точек графика
функции f(![]() ) =
) =![]() ,в которых касательная, проведённая
к графику функции, параллельна оси абсцисс.
,в которых касательная, проведённая
к графику функции, параллельна оси абсцисс.
5. Найдите площадь фигуры, ограниченной линиями
![]() ,
,![]()
6. Сумма длин стороны основания и высоты правильной четырёхугольной пирамиды равна 12 см. При какой длине стороны основания пирамиды её объём будет наибольшим?
Критерии оценки экзаменационной работы
На экзамене учащиеся должны показать: владение соответствующими математическими методами и приемами решения задач; четкое знание основных формул учебных разделов дисциплины; умение четко проводить математические рассуждения в письменном изложении; уверенное владение основными умениями и навыками, предусмотренными программой, умение применять их при решении задач.
Результаты контроля признаются положительными в случае, если обучающийся при сдаче работы получил отметку не ниже удовлетворительной.
При оценке в первую очередь учитываются показанные учащимися знания и умения.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Оценка ответа учащегося проводится по пятибалльной системе.
Критерии ошибок
|
Вид ошибки |
Имеющиеся недочеты |
|
Грубая ошибка |
Незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебных разделах дисциплины, а также вычислительные ошибки, если они не являются опиской |
|
Негрубая ошибка |
Потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им |
|
Недочет |
Нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях |
Оценка письменной работы
|
Оценка уровня подготовки |
Имеющийся результат |
|
|
Балл (отметка) |
Вербальный аналог |
|
|
5 |
Отлично |
Работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала) |
|
4 |
Хорошо |
Работа выполнена на 80-90 % или обоснования шагов решения недостаточны; допустима одна-две негрубые ошибки или два-три недочета |
|
3 |
Удовлетворительно |
Работа выполнена на 60-70 % или допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках. |
|
2 |
Неудовлетворительно |
Допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по учебной дисциплине в полной мере; работа показала полное отсутствие у учащегося обязательных знаний и умений или значительная часть работы выполнена не самостоятельно. |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.