
МКОУ «Сюгютская средняя общеобразовательная школа им.М.Митарова»
Конечные и бесконечные десятичные дроби
9 класс
Выполнила: учител математики
Сеферова М.М.
Конечные и бесконечные десятичные дроби.
Цели: Закреплять навыки замены десятичных дробей обыкновенными. Формировать умение преобразовывать обыкновенные дроби в десятичные. Познакомиться с понятием «конечные и бесконечные десятичные дроби». Научиться по знаменателю обыкновенных дробей определять такие, которые можно выразить конечной десятичной дробью. Формировать навыки работы на калькуляторе. Развивать умение выделять главное, существенное в изучаемом материале, стремление самостоятельно добывать знания. Воспитать настойчивость, познавательный интерес. Продолжить работу над речевой регуляцией действий.
I. Организационный момент.
«На сегодняшнем уроке вы продолжите знакомиться с увлекательным миром чисел. Углубите знания о десятичных дробях, научитесь по знаменателю обыкновенной дроби определять такие, которые можно выразить тем или иным видом десятичной дроби.
А задумывались ли вы над тем, всегда ли люди умели считать, всегда ли числа назывались так, как сейчас?»
II. Упражнения, связанные с развитием логического мышления.
1. Представьте себя на минутку первобытными людьми или древними пастухами, которые не умеют ни считать, ни писать, тем не менее они знали, не пропала ли хоть одна овца из их огромного стада. Как они могли это знать, не умея считать?
- (ответы учащихся)
2. У некоторых племен еще недавно не было других числительных, кроме «один» и «два». Все, что шло после двух, называлось «много». Но потом понадобилось назвать и другие числа. Ведь и собак и скота и стрел у охотника было больше, чем две.
Числа стали называть, повторяя несколько раз названия для единиц и двоек.
Например, у некоторых папуасских племен числительное «один» и сейчас звучит как «урапун», а числительное «два» как «окоза».
Число 3 они называли «окоза-урапун». 4 - ? 5 - ? 6 - ? А дальше число называли «много».
III. Проверка домашнего задания.
Сейчас достаточно много чисел имеют свои названия.
1. Назовите самое маленькое и самое большое число.
 2. Прочтите числа.
2. Прочтите числа.
Эти числа можно разделить на две группы.
3. Дополните схему.
![]()
![]() Числа
Числа
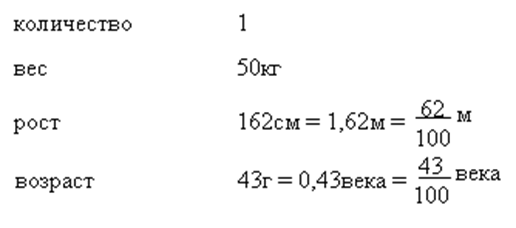
![]() В качестве примера используйте данные моих параметров.
В качестве примера используйте данные моих параметров.
а) Какое преобразование необходимо выполнить, чтобы записать десятичную дробь в виде обыкновенной?
(Записать со знаменателем и/или можно сократить)
б) Можно ли обыкновенную дробь записать в виде десятичной?
Назовите правило.
Сравните дроби:
3,56 … 5,9 1/2 < 0,625 => 0,5 < 0,625
0,16 … 0,9 2/5 … 3/4 => 0,4 < 0.75
IV. Объяснение нового материала.
Всегда ли можно до конца поделить числитель на знаменатель?
Об этом вы узнаете из упражнение № 586 на странице 104.
Ответить на вопросы.
1. Назовите два вида десятичных дробей.
2. Какая десятичная дробь называется конечной?
3. Какая десятичная дробь называется бесконечной?
V. Закрепление:
а) Запишите в виде десятичных дробей.
1/9 = 0,111 5/7 = 0,7142 3/15 = 0,2
б) С помощью калькулятора запишите десятичной дробью.
1/2 = 0,5 2/5 = 0,4 9/10 = 0,9 3/20 = 0,15 18/32 = 0,5625
3/4 = 0,75 5/6 = 8,33…8/11 = 0,72 6/25 = 0,24 1/40 = 0,025
2/3 = 0,666 3/8 = 0,375 4/16 = 0,25 7/24 = 0,29 17/50 = 0,34
40/64 = 0,625 8/65 = 0,123… 7/80 = 0,0875
Назовите знаменатели обыкновенных дробей, которые можно выразить конечной десятичной дробью.
В тетрадь:
Знаменатели обыкновенных дробей, которые можно выразить конечными десятичными дробями:
2, 4 , 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100, 200, 250, 500, 1000.
стр. 105 № 589 (комментировать письмо).
Выпишите обыкновенные дроби, которые можно заменить конечными десятичными дробями.
3/25; 6/1000; 4/9; 9/200; 7/16; 8/19; 11/500; 7/12; 4/27; 1/32; 2/5.
Самостоятельно:
Записать знаменатели обыкновенных дробей, чтобы при выражении их десятичной, дробь получалась конечной.
2/ ; 4/ ; 7/ ; 16/ ;
Задача: с. 96 № 545.

Ответ: Переработали 300 кг картофеля.
VI. Итоги урока.
1. Что нового вы узнали на уроке?
2. С Какими видами десятичных дробей вы познакомились?
3. Можно ли определить по знаменателю обыкновенной дроби вид десятичной дроби?
VII. Дома: стр. 106 № 593 (4 примера)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.