На
данном уроке рассматривается понятие алгебраической дроби. С дробями человек
встречается в самых простых жизненных ситуациях: когда необходимо разделить
некий объект на несколько частей, например, разрезать торт поровну на десять
человек. Очевидно, что каждому достанется по
части
торта. В указанном случае мы сталкиваемся с понятием числовой дроби, однако
возможна ситуация, когда объект делится на неизвестное количество частей,
например, на x. В таком случае возникает понятие дробного выражения. С
целыми выражениями (не содержащими деление на выражения с переменными) и их
свойствами вы уже познакомились в 7 классе. Далее мы рассмотрим понятие
рациональной дроби, а также допустимых значений переменных.
Определение и примеры алгебраических дробей
Рациональные выражения делятся на целые и дробные выражения.
Определение. Рациональная
дробь – дробное выражение вида 
,
где 
–
многочлены. 
–
числитель, 
–
знаменатель.
Примеры рациональных
выражений: 
– дробные
выражения; 
–
целые выражения. В первом выражении, к примеру, в роли числителя выступает 
,
а знаменателя – 
.
Значение алгебраической
дроби, как и любого алгебраического выражения, зависит
от численного значения тех переменных, которые в него входят. В частности,
в первом примере значение дроби зависит от значений переменных 
и 
,
а во втором только от значения переменной 
.
Вычисление значения алгебраической дроби и две основные задачи на дроби
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример
1. Вычислить значение дроби 
при
а) 
,
б) 
,
в) 
Решение. Подставим
значения переменных в указанную дробь: а) 
,
б) 
,
в) 
–
не существует (т. к. на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных – значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения.
Допустимые (ОДЗ) и недопустимые значения переменных в дробях с одной переменной
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример
2. Установить, при каких значениях переменной не имеет смысла
дробь 
.
Решение. Чтобы
данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель
дроби не равнялся нулю. Таким образом, недопустимыми будут только те
значения переменной, при которых знаменатель будет равняться нулю.
Знаменатель дроби 
,
поэтому решим линейное уравнение:
.
Следовательно,
при значении переменной 
дробь
не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных – знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример
3. Установить, при каких значениях переменной не
имеет смысла дробь
.
Решение. 
.
Ответ. 
.
Пример
4. Установить, при каких значениях переменной не имеет смысла
дробь 
.
Решение.
.
Встречаются
и другие формулировки данной задачи – найти область определения или область
допустимых значений выражения (ОДЗ). Это означает – найти все допустимые
значения переменных. В нашем примере – это все значения, кроме 
.
Область определения удобно изображать на числовой оси.
Для
этого на ней выколем точку 
,
как это указано на рисунке:
Рис. 1
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ.
.
Пример
5. Установить, при каких значениях переменной не
имеет смысла дробь 
.
Решение.
.
Изобразим полученное решение на числовой оси:
Рис. 2
Ответ.
.
Графическое представление области допустимых (ОДЗ) и недопустимых значений переменных в дробях
Пример
6. Установить, при каких значениях переменных не
имеет смысла дробь 
.
Решение.
. Мы получили
равенство двух переменных, приведем числовые примеры: 
или 
и
т. д.
Изобразим это решение на графике в декартовой системе координат:
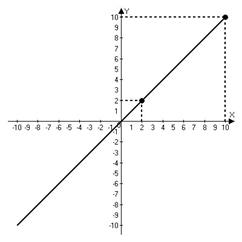
Рис. 3. График функции 
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. 
.
Случай типа "деление на ноль"
В
рассмотренных примерах мы сталкивались с ситуацией, когда возникало
деление на ноль. Теперь рассмотрим случай, когда возникает более интересная
ситуация с делением типа 
.
Пример
7. Установить, при каких значениях переменных не
имеет смысла дробь 
.
Решение.
.
Получается,
что дробь не имеет смысла при 
.
Но можно возразить, что это не так, потому что: 
.
Может
показаться, что если конечное выражение равно 8 при 
,
то и исходное тоже возможно вычислить, а, следовательно, имеет смысл
при 
.
Однако, если подставить 
в
исходное выражение, то получим 
–
не имеет смысла.
Ответ.
.
Чтобы
подробнее разобраться с этим примером, решим следующую задачу: при
каких значениях 
указанная
дробь равна нулю?
(дробь
равна нулю, когда ее числитель равен нулю) 
.
Но необходимо решить исходное уравнение с дробью, а она не имеет смысла
при 
,
т. к. при этом значении переменной знаменатель равен нулю. Значит, данное
уравнение имеет только один корень 
.
Правило нахождения ОДЗ
Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.
Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.
Разные задачи и выводы
Пример
8. Докажите, что при любых значениях переменной
дробь 
.
Доказательство. Числитель
– число положительное. 
.
В итоге, и числитель, и знаменатель – положительные числа, следовательно,
и дробь является положительным числом.
Доказано.
Пример
9. Известно, что 
,
найти 
.
Решение. Поделим
дробь почленно 
.
Сокращать на 
мы
имеем право, с учетом того, что 
является
недопустимым значением переменной для данной дроби.
Ответ.
.
На данном уроке мы рассмотрели основные понятия, связанные с дробями. На следующем уроке мы рассмотрим основное свойство дроби.
Скачано с www.znanio.ru
На данном уроке рассматривается понятие алгебраической дроби
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных
Решение. . Ответ. . Пример 4
Рис. 3. График функции Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби
Правило нахождения ОДЗ Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби : для нахождения
© ООО «Знанио»
С вами с 2009 года.
