Конспект открытого урока на тему:: «Сложение и вычитание десятичных дробей»

План-конспект  урока по ФГОС

Класс: 5

Предмет: математика.

Учебник: Математика, 5 класс,  Н.Я. Виленкин

Тема урока: «Сложение и вычитание десятичных дробей»

Тип урока: урок изучения и первичного закрепления новых знаний и способов деятельности.

Цель: организовать деятельность учащихся по восприятию, осмыслению и первичному закреплению новых знаний и приёмов сложения и вычитания десятичных дробей.

Методы: репродуктивный, проблемный, частично-поисковый.

Принципы обучения: научность, доступность, наглядность, сознательность, системность.

Оборудование: интерактивная доска, ноутбук, мультимедийный проектор, экран, слайды презентации, раздаточный материал - карточки с заданиями, учебник.

Временной режим: 45 минут.

Этап 2. Игра «Заполни пропуски»

Сравни числа

3,78 … 4,78               5,15 … 5,51

0,7 … 0,699               4,23 … 4,230

Запиши десятичную дробь в виде дроби или смешанного числа

6,1=                           0,003=

76,07=                       2,0002=       

Заполни пробел…

Озеро Байкал – самое глубокое место на земном шаре. Его глубина достигает 1622 м. или  км

Сибирский осётр – одна из крупных рыб. Длина его достигает 3 м, (км) вес более 100 кг (т).

Самое длинное животное - ленточный червь – был найден в прибрежных водах Южного моря. Его длина равнялась 54 м90 см . ( м)

Этап 3.

Учитель: Для всех учащихся предлагается задание, где надо провести соответствие ответа с буквой. В результате ваших действий должно получиться слово (СТЕВИН) - имя нидерландского ученого математика, открывшего десятичные дроби в Европе.

Задание. Приём «классификация задач по способу их решения». Задания проецируются через проектор на интерактивную доску, после выполнения задания ответы появляются на доске для сравнения с образцом.

 1) 
2) 
3) 
4) 
5) 9
6) 
7) 9-
8) 
9) 

Т – 16,4; С – 16,7; В – 2,01; Е – 16,3; И – 1,7; Н – 2,4.

Учитель: Сможешь ли ты выполнить это задание?

Ученик: Смогу, т.к. знаю правило сложения смешанных чисел.

Ученик: Затрудняюсь, т.к. не всегда получаю правильный ответ.

Учитель: В чем именно трудность?

Ученик: В данных дробях разные знаменатели ,не могу сложить.

Учитель: Есть ли другие способы решения?

Ученик: Полученное слово «СТЕВИН». Оставшиеся три задания характеризуют проблему.

Учитель: Какие еще способы возможно применить?

Ученик: С помощью поискового анализа, получаем, что выражения  №2, 6, 9 можно решить другим способом, переводя данные смешанные числа в десятичные дроби.

Итог работы записывается в тетрадь и на доске. Таким образом, учащиеся определяют тему урока, ставят цели и задачи своей деятельности. Определяют степень трудности, проводят прогнозирование своих действий, работают со шкалой самооценки, делают прогноз на результат.

Учитель: Итак, тема: «Сложение и вычитание десятичных дробей».

Учитель предлагает учащимся задания. 

А) Найди пропущенные слова (приём «неполное задание»)

1. Любое число,… (знаменатель) … дробная часть которого выражается единицей с одним или несколькими нулями, можно представить в виде… (десятичной дроби)…

2. После запятой ... (числитель) …дробной части должен иметь столько же цифр, сколько… (нулей) … в знаменателе.

3. Если в конце десятичной дроби … (приписать нуль) … или … (отбросить нуль) ..., то получится дробь, равная данной.

Ученики прописывают пропущенные слова в тетради.\, слайд с ответами проецируется на интерактивной доске.

Учитель: Найди ошибку. 

Ученик: Ошибки нет.

Б)Прием «перехода ситуации затруднения к поставленной учебной задаче».

9,3 + 7,4 =

7,004 + 9,4 =

9,3 – 7,4 =

9 – 7,4 =

Учитель:

В) Работая в парах, найти сумму десятичных дробей, приводя каждую дробь в смешанное число.

Задания б) и в) позволяют выявить на осознанном уровне умения и навыки по теме «Смешанные числа».

Г) Найди сумму десятичных дробей, используя запись столбиком.

Возможные варианты ответов:

9,4
+
7,004

7,004
+
9,4      

Уровень выполнения – творческий.

Учитель: При сложении смешанных чисел получили:

= 16,404

У вас 16,008 и 7,098.

Дети сравнивают ответы сложения смешанных чисел и десятичных дробей, приходят к противоречию. Учащиеся самостоятельно ставят задачи на основе соотнесения  условий в новой ситуации, ищут новые способы решения.

Анализ своих действий позволяет выйти на алгоритм выполнения задания.

Ученик: Если записать числа строго «запятая под запятой», добавить нули, то получим 16,404.

Алгоритм решения

1) Уравнять в десятичных дробях количество знаков после запятой.

2) Записать их друг под другом так, чтобы, запятая была под запятой.

3) Выполнить сложение (вычитание) не обращая на  запятую.

4) Поставить в ответе запятую под запятой в данных дробях.

Учитель: Какой способ работы был самым успешным?

Ученик: Способ решения записи сложения десятичных дробей – «запятая под запятой».

Учитель: Данный алгоритм сверим с алгоритмом в учебнике (стр.197) и записываем в «Тетрадь открытий».

Этап 5. 

Игра «5*5» (пять примеров за пять минут на оценку 5).

Для учащихся с сильной математической подготовкой выдаются карточки с разно-уровневыми заданиями.

Карточка №1

1. Найти сумму (разность):

А) 24,37 + 65,83 =

Б) 0,04 + 102 =

В) 0,24 + 70,043 =

Г) 453,24 – 324 =

Д) 880 – 8,033 =

2. Замените * цифрой так, чтобы получилось верное равенство:

9,4 = 9,*9 + 0,2*

Карточка 2

1. Найти сумму (разность):

А) 673,02 - 6,7302 =

Б) 20,04 - (6,064 + 10,04) =

В) 8345 - 83,45 =

Г) 37,873 - 24,5061 + 431,2 =

Д) 8800 + 8,8-88 =

2. Какие одинаковые цифры можно поставить вместо *,чтобы получить верное равенство: 0,18 = 1,* - *,62

Для учащихся со слабой и средней подготовкой предоставляются опорные конспекты «Реши по образцу».

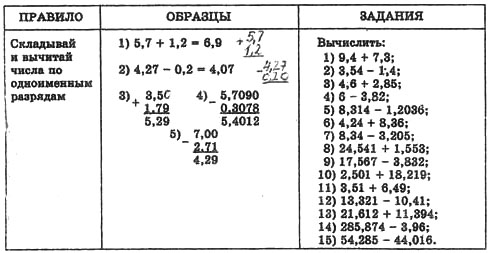
Проводится работа в группах по 2 человека. Ведется работа консультантов.

Методика «Способность детей ставить умные вопросы», «Обращение за помощью».