Конспект открытого урока по геометрии 8 класс «Трапеция. Средняя линия трапеции.»

Конспект открытого урока

 по геометрии 8 класс

 

«Трапеция. Средняя линия трапеции.»

 

Составила и провела :

Учитель математики Шамсудинова Тавус Жаватхановна.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тип урока: урок формирования новых понятий.

 

 

 

 

Цели урока :

 

-  образовательные :продолжить формировать понятия о многоугольниках; ввести понятия трапеции, ее элементов; рассмотреть виды трапеции и ее свойств ; применение полученных знаний к решению задач в стандартной ситуации и в измененных условиях.

 

 -воспитательные: формирование организованности ,дисциплинированности ,ответственности ,умение работать в коллективе.

 

-развивающие: формирование наблюдательности ,логического мышления ,внимательности , познавательного интереса ,развивать умение самоконтроля ,осознания темы ,постановки цели.

                                

                                           Ход урока

 

I Ученики работают с кроссвордом

 

                                   Тема «Многоугольники»

По  вертикали

1.Предложение ,истинность которого доказывается.

2.Фигура,состоящая  из 3-х точек , не лежащих на одной прямой и отрезков ,попарно их соединяющих.

3.Прямоугольник  с равными сторонами.

4.Сумма длин сторон многоугольника.

5.Геометрическая фигура ,являющаяся стороной многоугольника.

6.Точка пересечения медиан треугольника.

7.Отрезок ,соединяющий две не соседние вершины многоугольника.

8.Граница многоугольника.

 

Предложить учащимся найти ключевое слово.

 

 

 

 

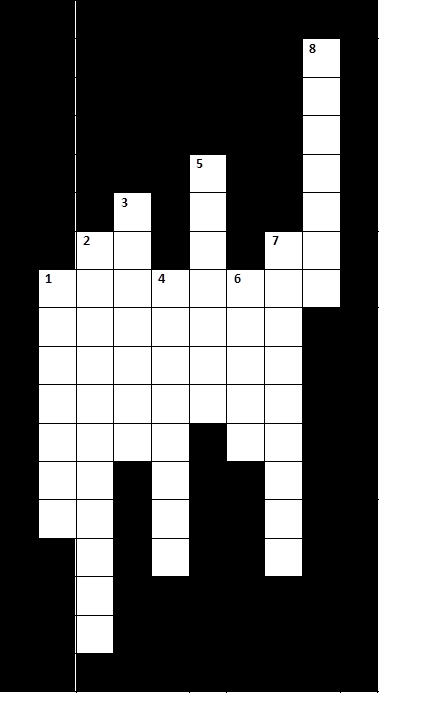
Если  ученик угадал правильно по всем вопросам ,то по горизонтали получается «Трапеция»

 

Кроссворд с ответами ниже.

Ⅱ  

 

 

 

 

 

 

 

 

 

 

 

II  Задачи из домашней работы(готовит ученик заранее)  

 Дано ∆  ABC: M AB

NBC; BN= NC

Доказать:

1)MNǀǀ AC

 

2)AM и  NC не параллельны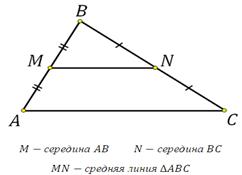

 

    

III Работа с классом.

 

 

На доске расположены пронумерованные многоугольники, разного цвета.

1,9,4,7- синие;  3,5,6,2 –зеленые ;8- розовый.

 

 

 

 

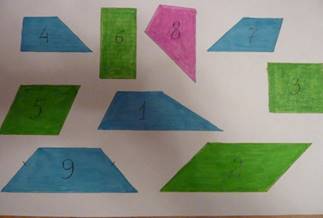
Ученик называет известные ему фигуры и дает определения.

Учитель предлагает рассмотреть оставшиеся фигуры (4,7,1,9) и просит учеников выделить общие свойства, которые их отличают от назвавших(Ответ: две стороны параллельны ,а две другие нет)

 Учитель дает название этим фигурам –трапеции.( подводит учеников к теме урока)

 

Итак ,записываем тему урока «Трапеция»

 

(обращаю внимание на кроссворд и домашнюю задачу-связь с темой урока)

  Еще раз учитель просит учащихся дать определение трапеции и вычерчивает на доске:

 

 

               

                                          B                            C                      ВС || АD

                                                                                                                          ABCD-трапеция

                                                                                                                          

                                                                                                  AB иCD не параллельны

               

                                   A                                           D         BC и  AD -основания

                                                                         AB и CD -боковые стороны

 

 

 

 

 

 

 

 

IV На доску поместить модели четырехугольников:

 

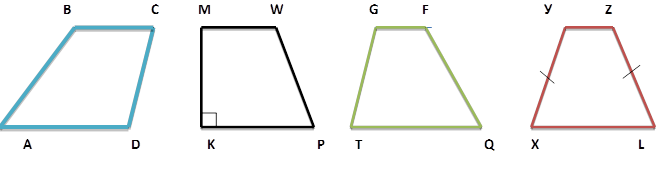
Учитель просит учащихся назвать трапеции, основания ,боковые стороны.

 

                                                    Виды трапеций

 

а)равнобедренная

б)прямоугольная

 

Попросить учеников дать определение равнобедренной и прямоугольной трапеций.

Итак, ученики повторяют определения трапеций ,их виды(сильный ученик ,средний и слабый)

Вопрос к учащимся :может ли равнобедренная трапеция быть прямоугольной ? (обсудить с учащимися)

 

 

 Задача (см.домашнюю задачу): верхушку стереть и получится трапеция.

I способ. AB и CD разделим пополам и соединим отрезком точки. Спросить ребят как называется отрезок?

 

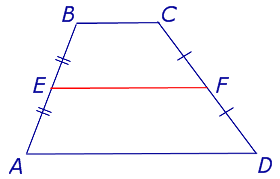
Читаем учебник п.59 стр.75

 

Дано:ABCD-трапеция

E AB ; AE=EB

EFǀǀ AD

 EF∩ CD=  F

 

Доказать :EF- средняя линия

 

  Доказательство:

1)    EF ǀǀ ADǀǀ BC

2)    Т.к. AE=EB (по условию ),то по теореме Фалеса  CF=FD=>F -середина  CD и по определению   EF- средняя линия трапеции.

 

(Отметки учитель ставит на заранее заготовленном листе со списком)

 

 

V Практическая работа

 

       Разделить класс на 4 –е группы

1)Ученики в тетрадях чертят произвольную трапецию

2)Измерить основания трапеции

3)Найти полусумму оснований

4)Начертить среднюю линию трапеции

5)Сравнить длину средней линии с полусуммой оснований

 

  Ребята выдвигают гипотезу  о свойствах средней линии и формулируют свои ответы (несколько человек)Читают учебник п.59 стр.75

 

VI Записываем в тетрадях «Средняя линия трапеции»

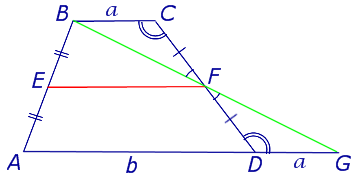
 Дано:

ABCD-трапеция

EF-средняя линия

 

Доказать :

1)EF ǀǀ AD

EF ǀǀ BC

3)    EF=1/2(AD+BC)

Доказательство(доказывает ученик ,который заранее его приготовил)

 

Учитель повторяет доказательство с учениками

1)BF∩ AD=G

2)∆FBC =∆FGD (по  стороне и двум прилежащим к ней углам)=>FB=FG;BC=DG

3)EF-средняя линия ∆ABG=>

a)EF ǀǀAG (EFǀǀ AD), но так как  BC ǀǀ AD ,то EFǀǀ BC(свойство  транзитивности)

б)EF= 1/2AG =1/2 (AD+DG)= ½(AD +BC),что тр.доказать

 

 

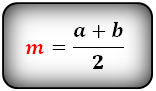где

а,в-длины оснований

m-длина средней линии

Доказательство повторяют по желанию несколько человек.

 

VII Решение задач по готовым чертежам ( устно)

1)Основания трапеции равны 7 см и 9 см.Чему равна средняя линия трапеции?

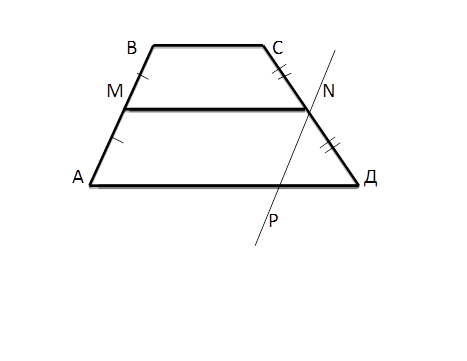
2)MN –средняя линия трапеции  ABCD(BCǀǀ AD).Через т.N проведена прямая ,параллельная стороне AB и пересекающая сторону AD в т.P. Доказать ,что  AMNP-параллелограмм.

 

3)В трапеции ABCD(BC ǀǀAD) известны стороны AB=4 cм,BC=5 см,

CD=6 см,AD=10 см.Чему равны стороны трапеции AMND,еслиMN-средняя линия трапеции ABCD

4)Участок ,занятый под фруктовый сад ,имеет форму трапеции.Деревья расположены параллельными между собой рядами,одинаково удаленными друг от друга.Во всех рядах расстояния между соседними деревьями одинаковые.В одном крайнем ряду 18 деревьев ,а в другом -26. Сколько деревьев в каждом из остальных рядов?

5) Средняя линия трапеции равна 8 см,а одно из оснований равно 6 см. Чему равно другое основание?

 

 

VIII Решение задач (письменно).Учащиеся записывают в тетрадь.

 

Средняя линия 8 см ,а одно из оснований   на 6 см больше другого.Найти основания(сделать чертеж и решить уравнением).Ответ: 5 см и 11 см.

 

IXДоклад (3 мин) (См. Глейзер « Из истории математики).

(откуда  произошло название «трапеция», история возникновения и развития понятия.)

 

XI Игра

«Внимательный геометр»

Спроецировать и ждать минуту ,потом попросить на доске написать название и сделать от руки чертежи ( в течение 3-х минут)

 

 

 

 

 

 

 

 

 

 

                  

 

 

 X Cвязь теории с практикой

 

Примеры из жизни (показать картинки):форму трапеции могут иметь скаты крыш,земельныеучаски,рюкзаки,одежда, гимнастические снаряды …

 

     

 

 

      

 

 

 

 

 

 

                                                                                                                             

 

XII Итог урока

 Что же мы узнали на уроке (трапеция ,средняя линия ,свойства средней линии)

Фронтальный опрос.Дополнительный вопрос:может ли диагональ трапеции

быть её высотой?

XIII Учитель объявляет отметки

 

XIV Задание на дом

(заготовить заранее на доске)

П.59 (в.17,18,19 )  повт.п.57 (в .15),упражнения№59,№69.

Для тех ,кто хочет знать больше  (доп.  задачи.)

 Задача №1. Доказать ,что отрезок, соединяющий середины оснований трапеции, делит среднюю линию пополам.

Задача№ 2 .Докажите способом от противного ,что средняя линия трапеции не проходит через точку пересечения диагоналей.

Задача№3.Как следует изменить длину оснований трапеции,чтобы средняя линия трапеции увеличилась в 2 раза?