Конспект урока

Тема урока: Свойства и график корня n-ой степени как функции обратной степени с натуральным показателем Цели урока: 

образовательные: рассмотреть свойства и график корня n-ой степени как функции

обратной степени с натуральным показателем; расширить и углубить знания о функциях; формировать умение распознавать данные функции по формуле и графику в зависимости от четности (нечетности) показателя, применять свойства функции при решении задач, строить графики.

развивающие: развивать внимание, логическое мышление; умение анализировать,

сравнивать и обобщать, делать выводы, развивать механизмы кратковременной и долговременной памяти.

 воспитательные: воспитывать графическую культуру, культуру устной и письменной

речи, аккуратность, дисциплинированность, ответственность. Побуждать учащихся к самоконтролю и саморефлексии своей деятельности

Средства: учебник, компьютер, проектор, интерактивная доска, презентация.

Тип урока: усвоения новых знаний

Ход урока: I. Организационный момент:  

Здравствуйте, студенты!

Мы сегодня с вами делаем новый виток в изучении функций, их графиков и свойств.  Эпиграфом к нашему уроку я предлагаю взять слова М. В. Ломоносова "Математику уже затем учить надо, что она ум в порядок приводит".

Поэтому, чтобы понимать, что мы будем делать на уроке, давайте сформулируем цели нашего урока:

-                     рассмотреть свойства и график корня n-ой степени как функции обратной степени с натуральным показателем;

-                     применять свойства функции при решении задач, строить графики. II. Актуализация знаний

Для изучения новой функции, необходимо вкратце вспомнить все, что мы с вами уже выучили по теме «Функции, их свойства и графики».  

Пройдите тестирование :

1.  Установите соответствие между понятиями и их определениями (каждый правильный ответ по 0,5 б)

2.  Выберите точку, принадлежащую графику функции y = (правильный ответ - 1 балл)

 a) (3; 9);         б) (16; 4);        в) (9; −3);       г) (16; −4). 

3. Найдите область определения функции у = √(х + 3)(х − 5) (правильный ответ - 1 балл)

a) [−3; 5];        б) (−∞; −3] U [5; +∞);          в) (3; −5);       г) (−∞;3) U (−5; +∞)

4.  Множеством значений функции y = 2 + 5 является промежуток (правильный ответ - 1 балл)

a) (0; ∞);      б) [0; ∞);      в) (5; ∞);      г) [5; ∞).  Выберите правильный ответ

5. Установите соответствие между графиками функций и формулами, которые их задают

(каждый правильный ответ по 0,5 б) 

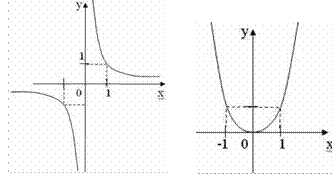
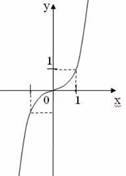
у = х^-5                                     у = х¹⁰                         у = х⁹ у = х^-6    у =                           

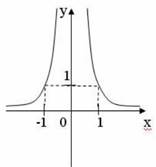
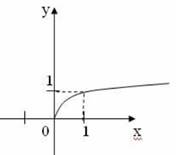
III. Изучение новой темы.

Вспомним основное определение корня:

Корнем n-ой степени из неотрицательного числа а при четном n называют такое неотрицательное число, которое при возведении в степень n дает в результате

число a. Записывается так: ^𝑛√a

Тогда как же выглядит график этой функции и, каковы ее свойства?

Из определения следует важный вывод:

На множестве значений 𝑥 ∈ [0; +∞) существует функция  при n=2,3,4, …, т. е. при любом натуральном n, не равном единице.

Записываем тему урока: Функции , их свойства и графики.

Вспомним степенную функцию с натуральным показателем y = xⁿ, где n – натуральный показатель и построим ее график. 

Рассмотрим случай, когда  n – четное натуральное число      и          n – нечетное натуральное число.

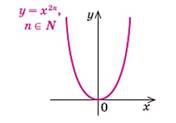
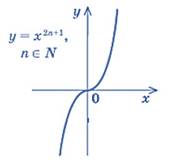
Область определения. Функция y = xⁿ (n – натуральное число) определена при всех x. Ее область определения – множество R. 

Нули функции. Функция обращается в нуль при x = 0. 

Знакопостоянство. 

Если n четно, то y ≥ 0 при всех x. 

Если n нечетное, то y < 0 при x < 0 и y > 0 при x > 0. 

Монотонность. 

Если n четно, то y убывает на промежутке (–∞; 0] и возрастает на промежутке [0; +∞). Если n нечетное, то y возрастает на всей числовой оси. 

Рассмотрим y = xⁿ, при x ∈ [0; ∞), она монотонна ⟹ функция обратима Найдем обратную функцию. Для этого  из равенства y = xⁿ выразим х:    

Выполним замену х →  у  получим y - обратная функция

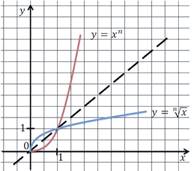
Построим график функции y = xⁿ при 𝑥 ≥ 0. 

График обратной функции y   симметричен графику функции y = xⁿ относительно прямой у = х

Рассмотрим свойства функции y    для четных и нечетных показателей корня. 

Функция y , где k ∊ N

1.    Область определения функции. 

По свойству арифметического корня D  [0; ∞). 

2.    Множество значений функции - E(y)  [0; +∞).

 Наибольшее  и  наименьшее значения функции. 

При x  0 функция принимает наименьшее значение y  0. 

Наибольшего значения у функции не существует. 

3.    Нули функции.  y  0 при x  0,  значение x  0 является единственным нулем функции. 

4.    Промежутки знакопостоянства функции.  y > 0 при всех x ∈ (0; +∞ ). 

5.    Промежутки монотонности функции. 

Функция возрастает на всей области определения. 

6.    Четность (нечетность) функции. 

Функция не является четной и не является нечетной, т.к. область определения функции не симметрична относительно начала координат.

7.    Ограниченность функции

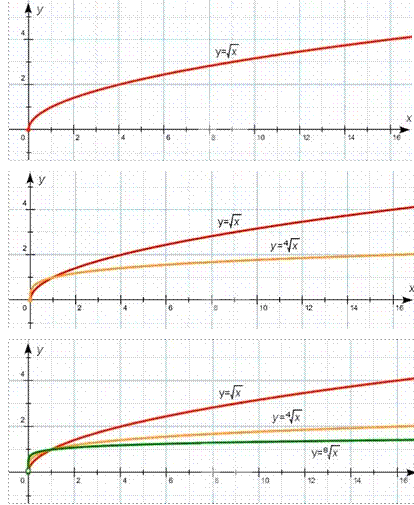
Функция ограничена снизу и не ограничена сверху 8.  График функции. 

Графики функций y xⁿ  при n  2, n  4, n  6 изображены на рисунке

Функция y = , где k ∊ N

1.  Область определения функции: D(у)  (−∞; ∞). 

2.  Множество значений функции: E(y)  (−∞; +∞). 

 Наибольшее  и  наименьшее значения функции: 

Наибольшего значения у функции не существует. 

3.  Нули функции: y  0 при x  0,  значение x  0 является единственным нулем функции. 

4.  Промежутки знакопостоянства функции: 

y > 0 при всех x ∈ (0; +∞ );              y < 0 при всех x ∈ (-∞; 0). 

5.  Промежутки монотонности функции: 

Функция возрастает на всей области определения. 

6.  Четность (нечетность) функции: функция является нечетной.  Её график симметричен относительно начала координат. 7. Ограниченность функции: Функция не ограничена 

8.   График функции. 

Графики функций y   при n  3, n  5 изображены на рисунке

IV.  Гимнастика для глаз

V.     Закрепление

№ 1. Найдите область определения функции:

Упражнения для самостоятельного решения: найдите область определения функции:

1). у = ;

2).  у =  2).    

№ 2. Найдите множество значений функции:

а) + 3;                   

б) f

Самостоятельная работа: 

1.Найдите множество значений функции:

а). у = ;

б).  у = ⁸√7х + 6 + 10 2.Найдите нули функции 

а)

б)у =  

3.Расположите числа   в порядке возрастания.

4.Расположите числа   в порядке убывания ³√5; √2;  ⁶√7 5. Постройте график функции:

а) f(х) =   + 2;                                  б) f(х) =

а) g 2;                                 б) g.

6. Какой (четной или нечетной) является функция:

а) f(х ) = ;               б) р(х ) = ;                        в) h(х ) = ⁵√|х|;                         г) g(х ) = . 

VI.        Итог урока. 

VII.     Домашнее задание.

VIII.  Рефлексия