Конспект урока по алгебре в 11 классе "Подготовка к ЕГЭ. Решение тригонометрических уравнений"

Тема урока: «Подготовка к ЕГЭ. Тригонометрические уравнения»

Цель урока: закрепить навыки решения тригонометрических уравнений различных типов в процессе подготовки к ЕГЭ.

Задачи урока.

·                    закрепление программных знаний и умений по решению тригонометрических уравнений;

·                        применение свойств тригонометрических функций;

·                    обобщение и систематизация материала;

·                    создание  условий для  контроля и самоконтроля  усвоения знаний и умений;

·                    исторические  сведения;

·                     воспитание навыков делового общения, активности;

·                    формирование интереса к математике и ее приложениям;

·                    формирование умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию;

·                    развитие познавательного интереса, математического кругозора, мышления и речи, внимания и памяти.

Ход урока

Мало иметь хороший ум, главное – хорошо его применять.

Рене Декарт.

1.                      Организационный этап

2.                      Устная работа

На слайде даны термины: тригонометрические функции, свойства и графики; основное тригонометрическое тождество; формулы приведения; формулы сложения; формулы двойного угла; формулы понижения степени (формулы половинного угла); тригонометрические выражения, тождества и уравнения.

Вопрос: как эти термины связаны между собой?

Действительно, сегодня у нас урок закрепления навыков решения тригонометрических уравнений различных типов в процессе подготовки к ЕГЭ. Мы повторим, обобщим и приведем в систему изученные виды, типы, методы и приемы решения тригонометрических уравнений. Надо сказать, что именно тригонометрические задания вызывают затруднения при сдаче экзаменов. 

Вопросы для обучающихся (учитель задает вопрос, обучающиеся отвечают и в подтверждение правильности ответа – слайд презентации):

1) Какие уравнения называют тригонометрическими?  (Уравнения, в которых переменная стоит под знаком тригонометрической функции, называются тригонометрическими).

2) Приведите примеры простейших тригонометрических уравнений?  (cos x = a; sin x = a;   tg x = a; ctg x = a)

3) Сколько корней может иметь тригонометрическое уравнение?  (Зависит от а: может не иметь корней, может иметь множество корней в силу периодичности тригонометрических функций).

4) Что значит решить тригонометрическое уравнение?  (Найти множество корней или убедиться, что корней нет)

5) В уравнениях cos x = a; sin x = a оцените число а?  (Если а<-1 и а>1, то нет корней).

6) Решите  простейшие тригонометрические уравнения

	при
	при

Напомните типы  тригонометрических уравнений и  методы их  решения

· Уравнения, сводящиеся к квадратным       a sin² x + b sin x + c = 0

· Однородные уравнения     а sin x +b cos x = 0                a sin² x + b cos²x +c  sin x cos x  = 0

· Уравнения, решаемые разложением левой части на множители   а(х) b(x) =0

· Уравнения вида        а sin x +b cos x = с

3.      Выполнение упражнений

Задание 1. Решите уравнение   8 cos⁴x +3 sin²x = 8

На столе – алгоритм решения уравнений

1.                      Определите тип уравнения

2.                      Наметьте план решения

3.                      Введите соответствующую замену переменной

4.                      Найдите область допустимых значений введенной переменной

5.                      Решите полученные простейшие уравнения

6.                      Запишите верно ответ

Учитывая, что из основного тригонометрического тождества sin²x = 1- cos²x, получим

8 cos⁴x +3 (1-сos²x)  = 8

8 cos⁴x -3 сos²x  - 5 = 0

Исходное уравнение свелось к  квадратному относительно     сos²x 

Пусть сos²x = t,   при условии  ,   тогда 8t²-3t-5=0,

откуда t₁=1,   t₂= -5/8-  не удовл.усл. t

cos² x =1,    cos x =,   x=,  

Ответ. x=,  

Задание 2. Решите уравнение   cos x – sin x=1.

Решение.

1 способ. Преобразование разности в произведение.           

cos x – sin x = 1

 

 

 

                               

 

                                  

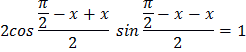
Ответ.    

2 способ.  Введение вспомогательного угла

              cos x – sin x=1,                      

Введем вспомогательный угол  такой, что         

Откуда       Значит,

Получим                               

   

 

Ответ.        

3 способ. Использование формул двойного угла.

      cos x – sin x=1

 

 

 

 

 

 

                                           

Ответ.      

 

4 способ.  С учетом множества значений функций

 

      cos x – sin x = 1                                                                                      

Разность косинуса и синуса одного угла может быть равна 1,  если

а)            и      б)                                                 

 

Откуда получим      

 

Задание 3. Решите уравнение   cos x + sin x = 7.

Решение.

Учитывая множество значений функций y=cos x   и  y=sin x, которыми являются отрезки  , сумма  не может быть равна 7. Поэтому, уравнение корней не имеет.

Ответ. Корней нет.

 

Тригонометрические выражения, уравнения и отбор корней присутствуют в заданиях ЕГЭ по математике базового и профильного уровней.

 

Задание 4.  (базовый уровень ЕГЭ)

Найдите значение выражения   

Решение.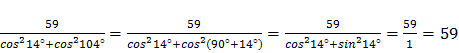   

Ответ. 59.

4.                      Тестирование (обучающиеся выполняют на бланках и сдают листы на проверку; после сдачи бланка на слайде появляются верные ответы)

№ п/п	Задание	Вариант ответа
		1	2	3	4
1	Вычислить cos 600				1
2	Вычислить sin 1200
3	Вычислить	0	1
4	Решить уравнение  cos x= -1	2Пп	П+2Пп	0
5	Решить уравнение  sin x = 1	2Пп	Пп
6	Решить уравнение  cos x=0		П	2П
7	Решить уравнение  tg x=1	600	900	450	1800
8	Упростите выражение
9	Упростите выражение
10	Упростите выражение

 

Исторический материал  (сообщение подготовлено 1 обучающимся заранее)

Обучающиеся, которые изучают свойства тригонометрических функций, решают уравнения, неравенства, пользуются функциями тригонометрии, должны помнить имя этого ученого.

Леонард Эйлер – крупнейший математик 18-го столетия. Родился в Швейцарии. Долгие годы жил и работал в России, член Петербургской академии.

Почему же мы должны знать и помнить имя этого ученого?

К началу 18 века тригонометрия была еще недостаточно разработана: не было условных обозначений, формулы записывались словами, усваивать их было трудно, неясным был и вопрос о знаках тригонометрических функций в разных четвертях круга, под аргументом тригонометрической функции понимали только углы или дуги. Только в трудах Эйлера тригонометрия получила современный вид. Именно он стал рассматривать тригонометрическую функцию числа, т.е. под аргументом стали понимать не только дуги или градусы, но и числа. Эйлер вывел все тригонометрические формулы из нескольких основных, упорядочил вопрос о знаках тригонометрической функции в разных четвертях круга. Для обозначения тригонометрических функций он ввел символику: sin x, cos x, tg x, ctg x.

На пороге 18-го века в развитии тригонометрии появилось новое направление – аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, то Эйлер рассматривал тригонометрию как науку о тригонометрических функциях. Первая часть: учение о функции – часть общего учения о функциях, которое изучается в математическом анализе. Вторая часть: решение треугольников – глава геометрии. Такие вот нововведения были сделаны Эйлером.

5. Выполнение упражнений

Задание 5. (профильный уровень ЕГЭ)

1) а) Решите уравнение    

    б) Найдите все корни этого уравнения, принадлежащие отрезку  

· Определите тип уравнения

· Наметьте план решения

· Выберите подходящий способ отбора корней тригонометрического уравнения:

- с помощью оси ОХ,

- с помощью единичной окружности,

- с помощью двойного неравенства,

- с помощью последовательного перебора целых значений n

Решение.

Решением данного уравнения является решение системы, состоящей из области определения логарифмической функции и решения тригонометрического уравнения.

1)    

Учитывая множество значений функций y= sin x   и  y=sin 2x, которыми являются отрезки     , сумма  может быть в промежутке (-2;2), а множество значений функции   заключено в промежутке (14; 18). Поэтому, неравенство        выполняется при любых значениях х. Значит, 

       

2)

                  

                           

                                 

Таким образом, получаем систему      

Значит, решением уравнения является      

б) Найдите все корни этого уравнения, принадлежащие отрезку  

 

x

              -4П                             -3П                      -2П                         - П                           0                         П          

Ответ. а)       

б)

Задание 6. При каких значениях а  уравнение   имеет корни. Найдите эти корни.

Решение   

Преобразуем правую часть уравнения 

          

Полученное уравнение имеет корни, если , откуда 

Таким образом, при         исходное уравнение имеет корни.

                                     

               

или           

     

Ответ. При       уравнение имеет корни        

6.Подведение итогов. Домашнее задание

Информация о домашнем задании и инструктаж о её выполнении.                                                                   1) по учебнику: №317(4) Решите систему уравнений, используя метод сложения 

2) ЕГЭ. Математика. Комплекс материалов для подготовки обучающихся, стр.79 

№5.1.14. а) Решите уравнение        

б) Найдите все корни этого уравнения, принадлежащие отрезку

3) подготовиться к тестовой работе по теме «Тригонометрия»

Итог урока.

Вывод:

- обобщили знания и отработали навыки решения тригонометрических уравнений различными способами, провели подготовку к ЕГЭ;

- развили чувство самостоятельности и ответственности за качество своих знаний;

- развили навыки самоконтроля, умений анализировать, составлять план или алгоритм учебных действий.