Конспект урока по математике для 10 класса "Действительные числа"

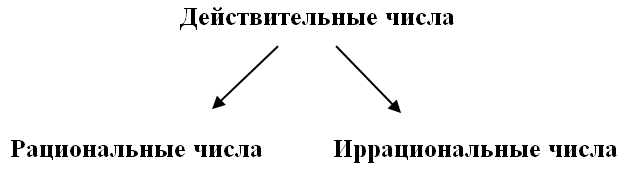
Действительные числа

Все числа, которые мы изучаем в школе, называются действительными числами. Они образуют множество действительных чисел, которые принято обозначать латинской буквой R.

В свою очередь все действительные числа можно разделить на 2 группы: рациональные числа и иррациональные числа.

Рациональные числа – это такие числа, которые можно записать в виде обыкновенной дроби , где m —целое число, n — натуральное число , обозначаются буквой Q.

Пример: -3; -0,5;  .

Иррациональные числа- это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.

Пример: π=3,141592…; 0, 113456... .

Рациональные числа, в свою очередь, можно разделить на 2 вида – это целые числа и дробные числа.

Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.

Целые же числа можно разделить еще на несколько групп: отрицательные целые числа, нуль и положительные (натуральные) целые числа.

На числовой оси (Ох) между целыми числами будут находиться дробные иррациональные числа. Все вместе они будут представлять собой множество действительных чисел, R.

Обратите внимание, что все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).

Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.

Числа 4; 4,2; 4,28 и т.д. являются последовательными приближениями значений суммы

 .

Пусть  это последовательные приближения действительного числа у с точностью до 1, до 0,1, до 0,01 и т.д. Тогда погрешность приближения  как угодно близко приближается к нулю.

 при  или 

Читается «модуль разности у и  стремится к нулю при n, стремящемся к бесконечности» или «предел модуля разности у и при n, стремящемся к бесконечности, равен нулю»

Т.е. если  при  или 

Модуль действительного числа у обозначается как |у| и определяется так же, как и модуль рационально числа:

.

А теперь давайте вспомним, что такое геометрическая прогрессия.

Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего (Рисунок 1).

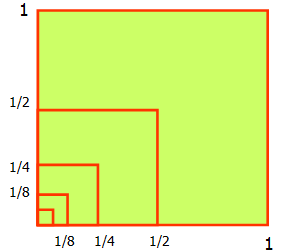
Рисунок 1

В результате, мы получили последовательность сторон квадратов  образующих геометрическую прогрессию со знаменателем .

И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,

n=15, ;

n=20, ;

n=21, .

Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.

Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников. (рисунок 2)

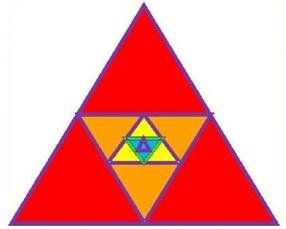
Рисунок 2

Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.

То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.

Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.

Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.

Определение:

Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.

Используя данное определение можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.

Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: (Рисунок 3)

Рисунок 3

Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1. 

Но в левой части этого равенства – сумма бесконечного числа слагаемых.

Рассмотрим сумму n первых слагаемых. 

По формуле суммы n первых членов геометрической прогрессии, она равна

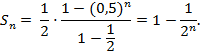
Если n неограниченно возрастает, то 

или . Поэтому , т.е. .

Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности 

Например, для прогрессии , где  ,

имеем 

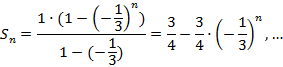
Так как то 

Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле

Примеры и разборы решений заданий тренировочного модуля

Пример 1: 

Воспользуемся калькулятором:

Найдем значение данного выражения с точностью до единиц.

Округлим полученные результаты до десятых:

Тогда получаем:

Найдем значение данного выражения с точностью до десятых.

Округлим полученные результаты до сотых:

3

Тогда получаем:

Найдем значение данного выражения с точностью до сотых.

Округлим полученные результаты до тысячных:

32

Тогда получаем:

 и т.д.

Пример 2.

Давайте выясним, является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:

а)  ; б) 

Решение:

. Найдем q.

;;

Следовательно, данная геометрическая прогрессия является бесконечно убывающей.

б)

Следовательно, данная последовательность не является бесконечно убывающей геометрической прогрессией.

Скачано с www.znanio.ru