Конспект урока по математике Единицы объема. Кубический метр и кубический дециметр

Единицы объема.
Кубический метр и кубический дециметр

Цели: познакомить с единицей объема «кубический метр»; учить выражать в кубических дециметрах кубические метры; формировать умение располагать данные объемы в порядке возрастания; решать задачи на определение объема.

Ход урока

I. Устный счет.

1. На чертеже найдите различные треугольники и квадраты. Сосчитайте, сколько всего квадратов на этом чертеже. Сколько здесь различных треугольников?

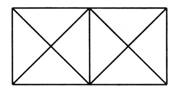
Ответ: квадратов – 3, треугольников – 26.

2. Прочитайте текст. Останкинская телевизионная башня в Москве состоит из железобетонной опоры высотой 384 м и металлической части, которая короче этой опоры на 229 м. Можно ли этот текст назвать задачей? (Нет.) Докажите. (Нет вопроса.) Подберите вопрос к данному условию. (Чему равна высота Останкинской башни?) Решите задачу.

3. Найдите правило нахождения числа, стоящего в средней клетке первой строки, и по этому правилу вставьте в пустую клетку пропущенное число:

II. Работа по учебнику.

Задание 6. Как можно назвать единицу объёма, которая равна объёму куба с ребром 1 м? (Кубический метр.)

Задание 7. Можно ли из 8 одинаковых кубиков составить куб? Покажите с помощью рисунка, как это сделать. Выразите в кубических метрах объём куба с ребром 2 м.

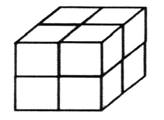
2 · 2 · 2 = 8 (куб. м)

Задание 8. На сколько отрезков длиной 1 дм можно разбить отрезок длиной 1 м? (На 10 отрезков.) На сколько квадратов со стороной 1 дм можно разбить квадрат со стороной 1 м? (На 100 квадратов.) На сколько кубов с ребром 1 дм можно разбить куб с ребром 1 м? (На 1000 кубов.)

– Объясните данное соотношение. 1 куб. м = 1000 куб. дм.

Задание 9. Во сколько раз нужно увеличить 1 дм, чтобы получить 1 м? (В 10 раз.) Во сколько раз нужно увеличить 1 кв. дм, чтобы получить 1 кв. м? (В 100 раз.) Во сколько раз нужно увеличить 1 куб. дм, чтобы получить 1 куб. м? (В 1000 раз.)

Задание 10. Выразите в кубических дециметрах.

5 куб. м = 5000 куб. дм               10 куб. м = 10 000 куб. дм

9 куб. м = 9000 куб. дм               45 куб. м = 45 000 куб. дм

3 куб. м = 3000 куб. дм

Задание 11. Выразите в кубических метрах.

2000 куб. дм = 2 куб. м

7000 куб. дм = 7 куб. м

10 000 куб. дм = 10 куб. м

Задание 12. Какую глубину имеет бассейн прямоугольной формы, если его длина 5 м, ширина 4 м, а воды в нем помещается 60 куб. м?

Решение: 60 : (5 · 4) = 60 : 20 = 3 (м).

Ответ: 3 м.

Задание 13. Учащиеся выполняют записи:

20 куб. дм · 5 = 100 куб. дм – объём 5 брусов.

20 куб. дм · 10 = 200 куб. дм – объём 10 брусов.

20 куб. дм · 50 = 1000 куб. дм – объём 50 брусов.

– Сколько брусов нужно взять, чтобы их общий объём составил 1 куб. м? (50 брусов.)

Задание 14. Учащиеся выполняют сложение и вычитание объёмов.

а) 2 куб. м 500 куб. дм + 3 куб. м 500 куб. дм = 6 куб. м;

б) 4 куб. м – 1 куб. м 300 куб. дм = 2 куб. м 700 куб. дм.

Задание 15. Расположите данные объёмы в порядке возрастания.

а) 5000 куб. дм;                           г) 5 куб. м 55 куб. дм;

б) 5 куб. м 5 куб. дм;                   д) 5 куб. м 500 куб. дм;

в) 5050 куб. дм;                          е) 5550 куб. дм.

Задание 16. Прочитайте задачу. Что известно? Что требуется узнать? Выполните схему и решите задачу.

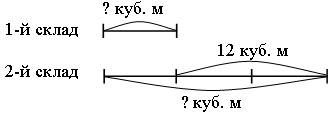
Решение: 1) 3 – 1 = 2 (ч.) – 12 куб. м;

2) 12 : 2 = 6 (куб. м) – на 1-м складе;

3) 6 · 3 = 18 (куб. м) – на 2-м складе.

О т в е т: 6 куб. м, 18 куб. м.

III. Итог урока.

– Назовите соотношение между кубическим метром и кубическим дециметром.

Скачано с www.znanio.ru