Конспект урока: Решение задач по теме «Теорема Пифагора»

Тема урока:Решение задач по теме «Теорема Пифагора» (8 класс)

Цель урока:направить деятельность учащихся на решение задач в использовании теоремы Пифагора в быту и применение теоремы Пифагора в нахождении площадей многоугольников

Задачи урока:

1) образовательная:углубление и систематизация теоретических знаний, отработка умений и навыков;

2)развивающая:  при работе на уроке учащихся познакомить с любопытными и историческими фактами из жизни с использованием теоремы Пифагора, развивая при этом познавательную активность ,логическое мышление, память, умение применять ранее полученные знания в навыке решении задач, повысить интерес к предмету;

3)воспитательная:умение работать в группе и индивидуально,воспитать умение контактировать с одноклассниками, воспитание чувство честности к себе и другим,чувство ответственности,взаимопомощи

Тип урока: урок-закрепление, совершенствование и развитие знаний,умений и навыков

Форма организации работы на уроке:групповая и индивидуальная работа

Методы обучения: частично-поисковый,фронтальный опрос,критическое мышление, объяснительно-иллюстративный

 

   План урока:

І.Организационный момент.Приветствие учащихся, проверка готовности к уроку,

    сообщение плана и целей урока

ІІ.Проверка домашнего задания. Актуализация знаний учащихся

ІІІ. Решение исторических задач

ІV. Решение задач на готовых чертежах с использованием теоремы

      Пифагора в нахождении площадей фигур

V. Подведение итога урока

VІ. Задание на дом

VІІ.Выставление и комментирование оценок

VІІІ.Рефлексия

 

 

Ход урока

І. Организационный момент.Приветствие учащихся, проверка готовности к уроку.

   Сообщение плана  урока.

-Сегодня мы постараемся ответить  на вопрос: Как теорема Пифагора применяется в жизни? В каких сферах деятельности применяется теорема Пифагора?

 

 ІІ. Проверка домашнего задания.

 

а)Актуализация знаний учащихся. Тест

 

 

            І вариант                                                           ІІ вариант

1.Выберите верное утверждение: А)площадь прямоугольника равна произведению двух его параллельных сторон; Б)площадь квадрата равна квадрату его сторон; В)площадь прямоугольника равна удвоенному произведению двух его соседних сторон	1.Выберите верное утверждение: А) площадь квадрата равна сумме  его сторон; Б) площадь прямоугольника равна произведению двух его противолежащих   сторон; В)площадь прямоугольника равна  произведению двух его соседних сторон
2.Закончите фразу:площадь ромба равна половине прозведению...... А)его сторон Б)его стороны и высоты,проведенной к этой стороне В)его диагоналей	2.Закончите фразу:  площадь параллелограмма  равна прозведению...... А)двух его соседних сторон Б)его стороны  на высоту,проведенную к этой стороне В)двух его противолежащих сторон
3.По формуле S=аha можно вычислить площадь: А)параллелограмма Б)треугольника В)прямоугольника	3.По формуле S=d1d2:2 можно вычислить площадь: А)параллелограмма Б)треугольника В)ромба
4.Площадь трапеции АВСД с основаниями АВ и СД и высотой ВН вычисляется по формуле: А) S=АВ:2∙СД∙ ВH; Б) S=(АВ+ВС):2∙ВH; В) S==(АВ+СД):2∙ВH	4.Площадь трапеции АВСД с основаниями  ВС и АД  и высотой СH вычисляется по формуле: А) S= СH∙(ВС+АД):2; Б) S=(АВ+ВС):2∙СH; В) S==(ВС+СД):2∙СH
5.Выберите верное утверждение: Площадь прямоугольного треугольника равна: а)половине произведения его стороны на какую-либо высоту; б) половине произведения его катетов; в) произведению его стороны на проведенную к ней высоту	5.Выберите верное утверждение: Площадь  треугольника равна: а)половине произведения его сторон; б) половине произведению его стороны на проведенную к ней высоту; в) половине произведения двух его сторон

Правильный ответ:

	1	2		3	4	5
І вариант	б	в	а		в	б
ІІ вариант	в	б	в		а	б

Проверка: взаимопроверка

Б)проверка домашней работы (ответы проговорить устно,а затем  решение задач показать на слаиде): №490(а,б),495(а),494-самопроверка, оценку в тетради ставят карандашом

№490(а,б)

А)                                      Дано:,АВ=ВС                         

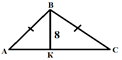            ВК=8 см, АС=12 см

                          Найти: АВ, S_АВС.

Решение: 1) ВК-высота и медиана в равнобедренном  АВС треугольнике.

Рассмотрим, АК=12/2=6 см

По теореме Пифагора  АВ²=ВК²+АК²=64+36=100, АВ АВ=10  (см)

І способ: 2) S_АВС=*ВК*АС=*8*12=48 (см² )                         Ответ: 10см, 48 см².

ІІ способ: 2) по формуле Герона р= 

==6*4*2=48 см².

 

Б)                               Дано:,АВ=ВС,∟В=90⁰

                                                ВК=7 см

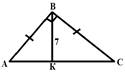        найти: АВ, S_АВС.

Шешуі: 1) ВК- высота,биссектриса и медиана в равнобедренном треугольнике:

Рассмотрим ,  ,  равнобедренный ,  АК=ВК= 7( см); АС=2*7=14 (см)

по теореме Пифагора   АВ²=ВК²+АК²=49+49=98, АВ АВ=7  (см)

І способ: 2) S_АВС=*ВК*АС=*7*14=49 (см² ) или S_АВС=*АВ*ВС=*7 *7  =49(см² )

                                                                                        Ответ : 7  см, 49 см².

ІІ способ: S_АВС=*АВ*ВС=*7*7=49 см².

№495(а)

                                    Дано:-трапеция

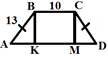                     ВС=10 см, АВ=ДС=13 см

                                             АД=20 см

                                  найти:  S_АВСД.

Решение: 1) ВК,СМ-высота, ВСМК-прямоугольник, КМ=ВС=10 (см)

АК=МД= (20-10)/2=5 ( см);

2) ,

По теореме Пифагора   ВК²=АВ²-АК²=13²-5²=8*18=144, ВК ВК=12  (см)

3) S_АВСД=*(ВС+ДА)*ВК=(10+20)*12=180 (см² )

Ответ: 180 см².

№494

                            Бер:-ромб

              АВ=10 см, ВД= 12 см

                            Т/к: АС, S_АВСД.

Шешуі: 1) АВ=ВС=АД=ДС=10 см,ВД┴АС, ∟О=90⁰, АО=ОС,ВО=ОД=6 (см),

2)

,

Из теоремы Пифагора  АО²=АВ²-ВО²=10²-6²=64, АО АО=8 (см),АС=2*8=16(см)

3) S_АВСД=*АС*ВД=*16*12=96 (см² )

Ответ : 16 см, 96 см².

 

ІІІ.Решение исторических задач:

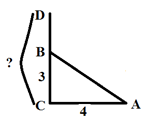
Задача №1индийского математика XII века Бхаскары

 

              На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в этом месте река

В четыре лишь фута была широка

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?

                                                    (1 фут 0,3 м) 

 

 

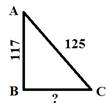
Задача №2 из учебника «Арифметика» Леонтия Магницкого

Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти нужно.

 

 

 

 

 

 

 

Задача №3 из китайской «Математики в девяти книгах»

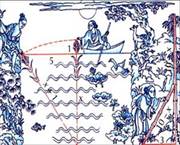Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?

 

 

 

 

 

        

 

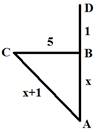
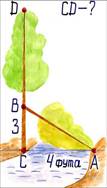
Задача №4 из древнего индийского учебника

 

 

 

 

 

 

 

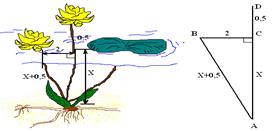
  На поверхности реки  на полфута от воды появился красивый цветок. Он был единственным на реке. В один ветреный день ветер унес его в сторону.Утром проснувший рыбак обнаружил цветок на расстоянии 2 фута от корня своего. Вопрос: какова глубина реки? (1 фут 0,3 м)

Решение:

Пусть глубина реки АС =Х , тогда AD = AB = Х + 0,5 .

Рассмотрим треугольник ACB, ∟С=90⁰

из теоремы Пифагора  AB² – AC² = BC²,

(Х + 0,5)² – Х² = 2² ,  Х² + Х + 0,25 – Х² = 4,      Х = 3,75.        3, 75 • 0,3 = 1,125 (м) 

Ответ : 3,75 фут или 1,125 м.

 

ІV. Решение задач на готовых чертежах с использованием теоремы Пифагора и нахождения площадей фигур

 

 

 

 

 

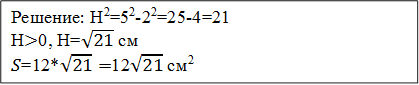
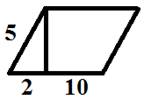
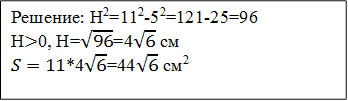
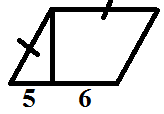
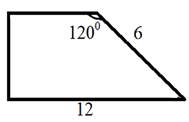
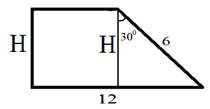
V. Подведение итога урока

Мы должна была ответить  на вопрос: Как теорема Пифагора применяется в жизни? В каких сферах деятельности применяется теорема Пифагора?

Таким образом, мы на уроке решили задачи из жизненного опыта.В настоящее время на рынке мобильной связи среди большая конкуренция среди операторов. Чем надежнее связь,чем больше зона покрытия, тем больше потребителей у операторов.При строительстве вышки(антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна,чтобы передача можно было принимать в определенном радиусе.

В строительстве красивых здании в виде пирамид и параллепипедов используется теорема Пифагора.

VІ. Задание на дом:№497,502,503

VІІ.Выставление и комментирование оценок

VІІІ.Рефлексия