Конспект урока "Серединный перпендикуляр" 7 класс

Задача 333

1 случай

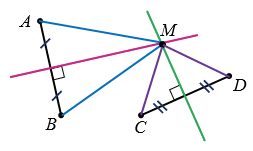
М - точка пересечения серединных перпендикуляров к отрезкам АВ и СD.

2 случай

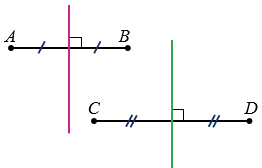
М - не существует.

3 случай

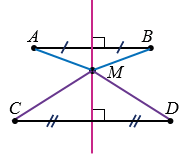
М - любая точка серединного перпендикуляра к отрезкам.

4 случай

М -  середина каждого отрезка и их точка пересечения.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Тогда возможны 4 случая расположения точки М в зависимости от расположения отрезков АВ и СD:

1 случай:

Если отрезки AB и CD не параллельны и не пересекаются (или пересекаются не в середине каждого из отрезков) то, чтобы построить точку М такую, что МА = МВ и МС = MD, нужно построить серединные перпендикуляры к каждому из данных отрезков и найти их точку пересечения, которая и будет искомой точкой.

2 случай:

Если отрезки AB и CD параллельны и середины этих отрезков не лежат на одной прямой, то такой точки М не существует, т.к. серединные перпендикуляры к отрезкам АВ и СD в таком случае не пересекутся (будут параллельны).

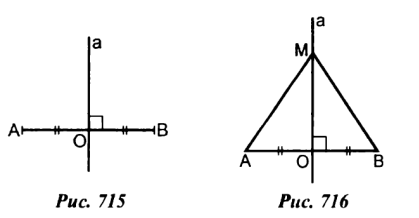
3 случай:

Если отрезки AB и CD параллельны и середины этих отрезков лежат на одной прямой, то за точку М можно взять любую точку серединного перпендикуляра, который является общим для двух данных отрезков.

4 случай:

Если отрезки AB и CD пересекаются в точке, которая является серединой каждого из них, то точка пересечения данных отрезков и будет искомой точкой М, т.к. серединные перпендикуляры к каждому из данных отрезков пересекутся в этой точке.

Задача 334

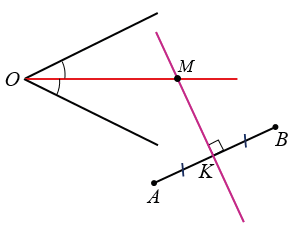
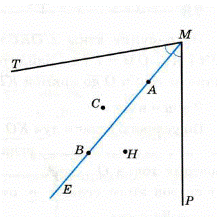
Искомая точка М - точка пересечения биссектрисы данного угла (ОМ) и серединного перпендикуляра к данному отрезку (КМ).

Пояснения:

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. А каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Следовательно, точкой равноудаленной от сторон угла и равноудаленной от концов отрезка, будет точка пересечения биссектрисы данного угла и серединного перпендикуляра к данному отрезку.

Задача 335