Конспект урока «Степенная и показательная функции, их свойства и графики»

БОУ ОО СПО «Орловский технический колледж»

Урок № ---

Тема: «Степенная и показательная функции, их свойства и графики»

Цели:

1.    научиться видеть графики степенной и показательной функций по формулам;

2.     определять по графику функцию;

3.     уметь анализировать графики;

4.     уметь сравнивать числа, решать неравенства с помощью графиков и свойств функций.

Воспитательные: Формировать умение работать самостоятельно.

Группа ___

Тип урока: Комбинированный.

План урока

I.                  Организационный момент.

II.                 Устный опрос.

1.    Какая функция называется показательной, а какая - степенной?

2.     От чего зависят графики и свойства степенной функции? Показательной функции?

3.     Через какую точку проходит график любой степенной функции?

III.          Из предложенных эскизов графиков выберите тот, который соответствует графику степенной (показательной) функции, у которой показатель

a.      Целое положительное чётное число

b.     Целое отрицательное нечётное число

IY. Опишите свойства функции

1). 2). 3). 4). 5). 6). 7). 8). 9).

Y.  Построить графики функции.

VI. Решить графически уравнение.

(x-1)-2/5=x2-3

Степенная функция. у = xn при n=2 – парабола

                                             при n=3 - гипербола

степенная функция - это функция вида у = х". Графики степенных функций n=1 и n=2 мы строили в 7 и 8 классе. При n=1 получаем функцию у=х, график - прямая. При n=2 получаем функцию у = х2, график которой - парабола. График функции n=3 - у = х3 называется параболой третьего порядка

VII . Выполнение тестовых работ:

Для  повторения и обобщения свойств показательной функции, обучающимся предлагается выполнить тест с последующей самопроверкой  и выставлением оценок. Ответы и критерии оценок на экране.

                                            Вариант 1

1.                  Упростите выражение 2^2x •2^-x +0,8⁰
А. 2^x+1.       Б. 2.     В. 2^-2x+0,8.    Г. 2^x +1

2.                  Показательная функция y=a^x убывает на R при …
А. a>1        Б.a  R    В. 0<a<1    Г.a>0

3.                  Какая функция является возрастающей?
А. y = 0,3^x   Б. y = 5^x В. . Г. y = 4^-x

4.                  График функции y = проходит через точку…
А.(1;1).       Б.(1;0).  В.(0;0).     Г. (0;1).

5.                  Область определения показательной функции.
А. (0; +∞). Б.  R.   В. [0; +∞). Г. (-∞;0).

6.                  Область значений показательной функции.
А.(- ∞;0).   Б. R.    В. (0;+∞). Г. (-∞;0).

7.                  Область определения функции
А.(1; +∞).   Б.(0; +∞).   В. (- ∞;1).  Г. [1; +∞).

8.                  Функция y = 3^x возрастает на множестве чисел…
А. (0;1).     Б. R.     В. (1; +∞ ).  Г. (-∞ ;1)

                               Вариант 2

1.                  Область значений степенной функции.
А. (-∞; 0).   Б. R.   В. (0; +∞).   Г. (-∞;0).

2.                  Область определения степенной функции.
А.(0;+).   Б. R.   В. [0; +∞).    Г. (-∞; 0).

3.                  Степенная функция y = х^а убывает на R при…
А. a > 1.  Б. a  R.    В. 0 < a < 1.   Г. a > 0.

4.                  Степенная функция y = х^а возрастает на R при...
А. a > 1.   Б. a  R.    В. 0 < a < 1.   Г. a < 1.

5.                  Упростите выражение х^5а •х^-5а.
А. 1.          Б. 0.           В. 7^x.              Г. 7^-25x.

6.                  Какая функция является убывающей на R?
А. y = 0,75^x.    Б. y = 3^x.       В. y = ()^x       Г. y = 1,5^x.

7.                  График функции y = х² проходит через точку…
А. (1; 1).           Б. (1; 0).     В. (0; 0).            Г. (0; 1).

8.                  Область определения функции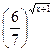  
А. [-1; 1].           Б. R.           В. [-1; +∞).       Г. [0; +∞).

        Критерии оценок:

8  правильных заданий - «5»

6-7 правильных заданий –«4»

4-5 правильных заданий – «3»

Вопросы:

№1. Какое уравнение называется показательным?

(Уравнение вида , где  и

Показательное уравнение - это уравнение, в котором переменная находится в показателем степени)

    №2. Теорема. Если  ,и , то

    №3. Назовите основные свойства степеней с       одинаковыми основаниями?

    №4.*С какими методами решения уравнений вы знакомы?

4. Разбор различных методов решения показательных уравнений.

Обучающимся предлагается рассмотреть предложенные степенные и  показательные уравнения, выбрать метод решения и решить уравнения.

1.

2.

3.

4.

5.

6.

Решения:

1. (Согласно теореме и свойству степеней с одинаковыми основаниями.) 

          х=3

Ответ: 3

 2.

 Ответ: 2;3

3. Приведение степеней к одному основанию

Ответ:

1.                         Вынесение Общего множителя за скобку (степени с наименьшим показателем)

Ответ: 1,5

2.                        Деление обеих частей уравнения на степень.

т.кто,

Ответ:3

3.                        Метод замены переменной

Замена: , у> 0, тогда

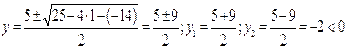
Обратная замена:

Ответ: 1

Итог урока:

Домашнее задание п. 35, № 447 б, 453

Преподаватель                                              Семиохина Л.А.

Скачано с www.znanio.ru