Конспект семинарского занятия по математике на тему "Интеграл и его приложения" (применение системного оператора и матричного метода)

Министерство образования и науки Челябинской области

Государственное бюджетное профессиональное образовательное учреждение

 «Южно-Уральский многопрофильный колледж»

Матричный метод в проведении семинарского занятия  по теме:

 «Интеграл и его приложения»

ДИСЦИПЛИНЫ «МАТЕМАТИКА»

Для специальностей, реализующихся на базе основного общего образования

г. Челябинск, 2017

Составитель: Е.А. Кондратьева, преподаватель математики

Рецензенты: М.А. Вуйлова, преподаватель математики, методист  ГБПОУ «Южно-Уральский многопрофильный колледж»

                        Л.И. Кундель, преподаватель математических дисциплин, методист ГБПОУ

                        «Челябинский техникум текстильной и легкой промышленности»

В конспекте представлены теоретическая часть матричного метода и его функции 4 видов проверки знаний и умений обучающихся. Рассматривается обоснование выбора матричного способа в проведении 5 видов семинара, как одной из активных форм обучения студентов и план занятия - семинар  «Интеграл и его приложения»: полный ход занятия с расшифровкой каждого этапа деятельности преподавателя и обучающихся. Часть времени занятия  отводится оценке обучающихся  через  балльно-рейтинговую  систему как инструмент  системы зачётных единиц.

Выделены упражнения и задачи для выполнения практических занятий через обязательные результаты обучения в соответствии с рабочей программой дисциплины «Математика». 

На занятии, вывод по теме, рассматривается через системный оператор. Конспект занятия  входит в КУМО дисциплины «Математика» для  студентов 2 курсов гуманитарных  направлений ССУЗов.

Введение

Матричный метод в проведении уроков по  математике – способ  использования комплекта  специальных  (тематических) заданий по математике, записанные в форме  матрицы (по строкам 1,2,3,… и столбцам А,В,С,…) предназначенный  для  формирования  умений  решать  упражнения  и  осуществлять контроль за  усвоением изученного

Матричный способ преподавания                                        математики

Каждая  матрица  содержит  более  5  заданий.  Структура  и  содержание  матриц  предусматривает постепенное  знакомство  с  темой,  усвоение  знаний,  формирование  навыков,  совершенствование  техники  оперирования  с  основными  контрольно-измерительными материалами,  усвоение  алгоритмов  решений  указанных  единиц  рабочей  программы.

Последовательность  расположения  заданий  матрицы  позволяет  варьировать  постановкой  упражнений,  что  ПОЗВОЛЯЕТ  ИСПОЛЬЗОВАТЬ  МАТРИЧНЫЙ  МЕТОД   на  всех  этапах  обучения  математике  ПРОГРАММЫ  «ШКОЛА-КОЛЛЕДЖ-ВУЗ»,  так  и  для  контроля  знаний и умений  студентов.

Задания  1  строки – самые  легкие,  задания  последующих   строк  постепенно  усложняются,  но  уровень  трудности  большинства  из  них  соответствует  стандартным  упражнениям  рабочей  программы.  В  столбцах   каждой   строки  имеет  место  задания  с  более  сложными  условиями,  а  небольшая  часть  из  них  относится  к  заданиям  повышенной  трудности.

Итак, от  уровня последовательности  решения  примеров  какого-либо   конкретного  столбца   позволяет   студентам  совершенствовать  необходимые  умения   и  навыки  и  доводить  их  до  самого  высокого. 

Матричный способ очень удобен в проведении семинаров разных видов:

1. Семинар-беседа – в форме развернутой беседы по плану семинара с кратким вступлением и заключением преподавателя, с применением матрицы упражнений по теме семинара – это позволяет вовлечь большинство студентов в активное обсуждение темы через заслушивания большого количества студентов по вопросам плана, дополнений других, рецензирования выступлений, постановки проблемных вопросов.

2. Семинар-заслушивание и обсуждение докладов, презентаций и рефератов  предполагает предварительное распределение вопросов между студентами и подготовку ими докладов, презентаций и рефератов. При этом выделяют 3 части:

v вступительную (тема, ее значимость);

v основную (излагается содержание темы);

v заключительную (обобщается тема, делаются выводы).

Особое внимание уделяется на доказательность и убедительность с привлечением матрицы – вопросов.

3. Семинар-диспут – коллективное обсуждение какой-либо проблемы с целью установления путей ее достоверного решения. Это предполагает:

v высокую умственную активность;

v прививает умение вести полемику, обсуждать информацию;

v защищать взгляды и убеждения;

v лаконично и ясно излагать свои мысли;

v составление матрицы -  заданий для работы на семинаре.

4. Смешанная форма занятия – это сочетание обсуждения докладов, свободных выступлений студентов, дискуссионное обсуждение с привлечением матрицы всех видов.

5. Семинар-практикум включает разрешение теоретических и практических вопросов через использование матрицы, упражнений по данной теме. Все это можно выразить в форме схемы:

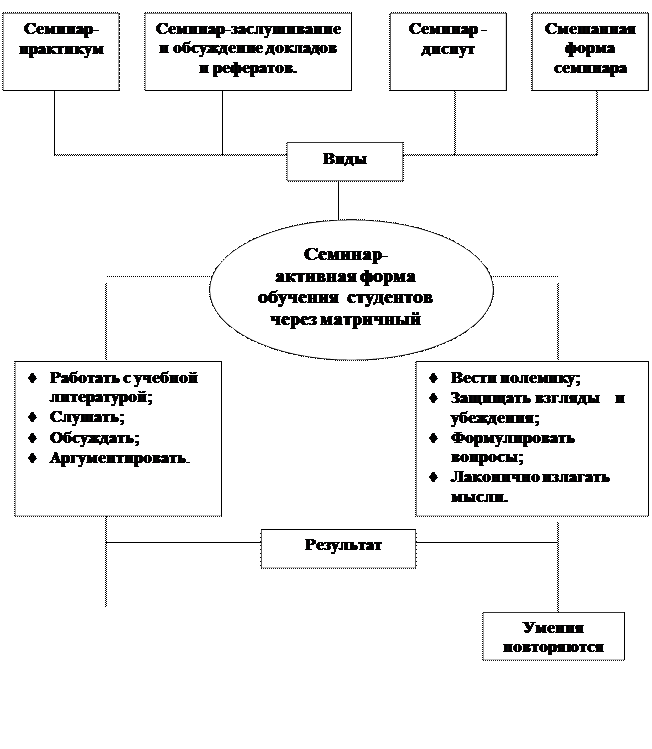
Семинар по теме  «Интеграл и его приложения» - это форма коллективной и самостоятельной работы студентов на уроке, которая способствует углубленному изучению учебного материала и формированию компетенций по теме.

За 2-4 недели до семинарского занятия студентам предлагаются вопросы для подготовки, литература для самообразовательной и самостоятельной работы, а отдельным студентам – творческие задания в форме небольших проектов, презентаций, сообщений, докладов, рефератов и т.д. В ходе подготовки к семинару, обучающие сами решают, в какой форме будут реализовывать  план; либо в форме устных ответов-сообщений, либо в форме презентаций, либо в форме тестов и т.д., но готовятся все и по всем вопросам.

В результате студенты совершенствуют творческие умения, учатся убедительно обосновывать и аргументировать свои выводы, опираясь на знания, полученные на уроке и в ходе подготовки к нему, а значит, и используют, и создают различные формы выражения информации по вопросам семинара, а также формируют компетенции.

       Урок, проведённый в такой форме и построенный на сочетании выполнения творческих заданий и дифференцированных практических работ, позволяет учитывать индивидуальные способности  и  интересы студентов. Такие занятия помогают лучше усваивать отдельные положения темы, а значит реализовывать и добиваться результатов в разрешении моей методической темы          «Практическая направленность преподавания  математики   через   самостоятельную деятельность  студентов и применение системного оператора – резерв повышения качества знаний»

ПЛАН  ОТКРЫТОГО ЗАНЯТИЯ

Учебная  дисциплина «Математика»

Преподаватель: Кондратьева Е.А.

НОМЕР ГРУППЫ: ПС-205

СПЕЦИАЛЬНОСТЬ:  40.02.01 «Право и организация социального обеспечения»

ТЕМА ПРОГРАММЫ: 1.7. Приложения определенного интеграла

ТЕМА ЗАНЯТИЯ: Интеграл и его  приложения.

ПЛАН: 1.История создания интеграла.

             2.Определения, свойства, виды, методы  вычисления интегралов.

             3. Практикум по вычислению  интеграла.

             4. Приложения интеграла.

ТИП ЗАНЯТИЯ: повторительно – обобщающий

Вид занятия: семинар

Уметь:

·        Выполнять вычисления интегралов разными методами.

Знать:

·        Определение интеграла. Виды интегралов. Свойства интегралов.

·         Основные способы  (методы)  вычисления  интегралов.

Цели занятия:

1)          Обучающая:

·                   Закрепить и систематизировать знания студентов  по определению, свойствам и методам вычисления интегралов элементарных функций.

·                   Формировать практические навыки.

2)           Развивающая:

·                   Развивать у обучающихся умения самостоятельно выполнять задания.

·                   Развивать умение находить связь между теоретическими знаниями и практическими умениями.

3)          Воспитательная:

·                   Воспитывать аккуратность, исполнительность и самостоятельность.

·                   Мотивировать необходимость воплощения теоретических знаний в практику.

Тип занятия: Закрепления и совершенствования знаний и умений.

Методы обучения:

а) словесно-наглядно, практический;

б) проектный;

в) интерактивный:

·                   педагог не дает готовых знаний, но побуждает студентов к  самостоятельному поиску через системный оператор;

·                   задача преподавателя: создание условий  для инициативы студентов и выполнение лишь роли помощника в работе одного из источников информации;

·                   постоянное взаимодействие педагога и студентов, но активность преподавателя  уступает (значительно)  активности студентов;

·                   коммуникация между студентом и преподавателем, самими студентами осуществляется через взаимодействия: «студент-студент», «студент-группа-студент» (работа в микрогруппах), «студент-аудитория», «группа студентов – аудитория» (презентация), «студент-ПК»;

·                   взаимодействие студентов друг с другом, консультирование друг друга и взаимообучение проводимое самими студентами.

 Вид занятия: Семинар.

Оснащение занятия:

1.Методические рекомендации для самостоятельной работы студентов в подготовке к семинарскому занятию на тему: «Интеграл и его приложения». Специальность 40.02.01 «Право и организация социального обеспечения».

2.Критерии оценивания (теоретической  и практической частей семинара и подведение итога). (Приложение С).

3.Электронное сопровождение занятия (презентации студентов). (Приложение В).

4.Дидактический материал к занятию (набор заданий по вариантам в форме матриц). (Приложение А).

5.Музыкальное сопровождение семинара (приложение D)

5.Схема «Интегральные и дифференциальные исчисления» (оформление кабинета).

6.Ноутбук с папкой «Семинар по теме «Интеграл и его приложения» (Приложения  А, В, С, D).

7.Портреты математиков: И.Ньютона, Г.Лейбница и др.

8.На экране слова «Напрасно думают, что она (фантазия) нужна только поэту. Это глупый предрассудок! Даже в математике она нужна, открытие дифференциального и интегрального исчисления невозможно было бы без фантазии».

9.Электронный курс учебной дисциплины «Математика» в АСУ ProCollege (ЮК ПСО) 0.40 ЕН. Занятие 16.

Литература и перечень рекомендуемых Интернет-ресурсов:

  Основная:

1.                 Богомолов Н.В.  Математика: учебник для  ССУЗов  /Н.В. Богомолов, П.И. Самойленко .- 3-е изд., стереотип.- М.: Дрофа, 2013.-395с.

2.   Богомолов Н.В. Практические занятия по математике: Учебное пособие для ССУЗов  / Н.В.Богомолов.-5-ое изд., стер.- М.: Высшая школа,  2012.- 495с.

Дополнительная:

1. Башмаков М.И. Алгебра и начала анализа: учебник  для 10-11 классов  средней  школы/ Башмаков М.И-3-е изд.-М.: Просвещение, 2011.-351с.

2. Высшая математика для экономистов: учебник для студентов ВУЗов/ под редакцией Н.Ш. Кремера.-3-е изд.- М.: ЮНИТИ - ДАНА, 2013.-479 с.- (Серия «Золотой фонд российских учебников»).

3.Комплект практических заданий для практических занятий дисциплины «Математика», часть 3 /под редакцией преподавателя ГБПОУ «ЮУМК»  Кондратьевой Е.А.-Ч.: ЮУМК, 2015 г. – 75с.

4. Математика для техникумов. Алгебра и начала анализа: учебник [Текст]. Ч.1/ М.И. Каченовский, Ю.М. Колягин, А.Д. Кутасов, Г.Л. Луканкин, и др.;  под ред. Г.Н. Яковлева. – 3-е изд. перераб. – М.: Наука, 2015. – 464с.

5. Пехлецкий И.Д. Математика: учебник для средних специальных учебных заведений/И.Д. Пехлецкий. -5 изд., стер.- М.: Академия, 2015г.-421с.

6. Опорный конспект по алгебре и началам анализа /под редакцией преподавателя ГБОУ  СПО (ССУЗ)  «ЮУМК» Кондратьевой Е.А.-Ч.: ЮУМК, 2013 г. – 56с.

7. Опорный конспект по геометрии /под редакцией преподавателя ГБОУ  СПО (ССУЗ)  «ЮУМК» Кондратьевой Е.А.-Ч.: ЮУМК, 2013 г. – 64с.

8. Яковлев Г.Н.Алгебра и начала анализа: учебник для ССУЗов/под редакцией Г.Н.Яковлева .- 3-е изд., перераб.- М.: Наука, 2009- 464с.

Перечень рекомендуемых Интернет-ресурсов:

1. Сайт Министерства образования РФ - www.mon.gov.ru

2. Образовательный математический сайт - www.exponenta.ru

3. Сайт всем кто учится-  http://www.alleng.ru

4.Сайт Южно-Уральского многопрофильного колледжа - http://www. suvc. ru/, /O:\Students_dfs\ForStudents\математика ЮК. ЮУМК

5.Сайт Южно-Уральского многопрофильного колледжа - http://www. suvc. ru/, учебный портал колледжа АСУ ProCollege,  электронный курс дисциплины «Математика» ЮК. ПСО (01- 03)

Междисциплинарные связи:  Приложения интеграла в физике, геометрии.

Формирование компетенций:

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.

Структура занятия:

1.     Организационный момент 2 мин.

2.     Сообщение темы и постановка целей 3 мин.

3.     Актуализация опорных знаний 12 мин.

4.     Вводный инструктаж 5 мин.

5.     Основная часть (теория, практика, итог) с инструктажем 60 мин.

6.     Подведение итогов занятия 5 мин.

7.     Домашнее задание 3 мин.

Ход занятия:

Элементы внешней структуы урока	Элементы внутренней (дидактической) структуры урока	Задачи этапа	Деятельность преподавателя	Деятельность обучающихся	Результат, формируемые общие компетенции (ОК)
1 Вводная часть	1.1. Организационный момент	Организовать обучающихся к работе	Приветствие, определение отсутствующих, проверка готовности обучающихся к уроку.	Приветствуют преподавателя, готовятся к уроку, получают на руки папки для практических занятий	Готовность группы к уроку ОК3
	1.2. Целевая установка и мотивация к уроку	Поставить четкие цели урока и наметить план их достижения. Мотивировать обучающихся к выполнению заданий семинарского занятия	Раскрывает цели занятия и план его проведения. Проводит мотивацию, опираясь на межпредметные связи и необходимость знания данного материала для изучения спецдисциплин. (Приложение B4)	Слушают, записывают тему и цель семинарского  занятия	Группа нацелена на выполнение заданий семинарского занятия. Обучающиеся мотивированы на учебно-познавательную деятельность.            ОК4
	1.3. Актуализация опорных знаний и опыта обучающихся	Выявление и устранение пробелов в знаниях.	Проводит фронтальный опрос (обзорно), слушает и комментирует ответы: 1)      Определение интеграла. 2)      Виды интегралов. 3)      Свойства интегралов. 4)      Методы вычисления интегралов. 5)      Приложения интегралов. 6)      История создания интегралов. Показ презентации Применение системного оператора. Интегралы. Виды. Свойства. Вычисления. Методы.	Отвечают на вопросы преподавателя, слушают комментарии к ответам и дополнения согруппников. Просмотр презентации.   (Приложение B3)	Пробелы  в знаниях выявлены, проведена работа по их устранению. ОК3,5
	1.4. Вводный инструктаж	Дать четкие указания по рассмотрению вопросов семинара	Доводит до обучающихся этапы ответов на вопроы семинара и критерии оценивания:  За каждый рассмотренный правильно и обоснованно вопрос с применением презентации 1 балл.  (Приложение C1).      Критерии оценки семинарского занятия: «5»-Работа должна быть выполнена правильно и в полном объёме , 90-100% выполнения. (1,8-2,0 балла) «4»-Работа выполнена правильно, но имеются недочеты,  процент выполнения 75-89%.(1,5-1,79 балла) «3»- Работа выполнена правильно, но имеются ошибки, процент выполнения 65-74%. (1,3-1,49 балла) Примечание: Под работой понимается устные и письменные ответы на занятии.	Слушают и оформляют работу  по семинарскому занятию.	Группа ознакомлена с критериями оценивания. Обучающиеся готовы к рассмотрению вопросов семинара и самостоятельному выполнению практической части в форме практической работы.
2. Основная часть	2.1. Систематизация  знаний                             2.2. Активизация теоретических знаний.                                                 2.3. Самостоятельное выполнение заданий.	Структурировать  полученные знания.                             Активизировать теоретические  знания.                                                 Самостоятельность получения результата, с последующем обоснованием выбранного способа в решении	Приступает к обсуждению   вопросов семинара. Вопрос №1. «История создания интеграла»       Вопрос № 2  «Определения, свойства, виды,  методы вычисления интегралов».             Активизирует знания по вопросу № 2 на основе: а) примера:    ==                                                           =lnx-=в) найти методы  интегрирования  в следующих примерах и обосновать свой выбор».         Работают самостоятельно по заданиям № 2, 7, 13, 16	Студентки (Яна Н, Елена Л.)  рассказывают историю вопроса  на основе презентаций,  делают выводы.  (Приложение B6, 7)   Студентки (Эльмира И., Наиля В., Женя П)  рассматривают вопрос  на основе своих презентаций и показывают важность изучаемых вопросов.  (Приложение B8, 10, 11)     Студенты раскрывают теоретические  понятия «неопределённого интеграла», «свойства неопределённого интеграла»; понятие   «определённого интеграла», «свойства определённого интеграла» на основе определений и формул.                   Работают  с помощью  матрицы -- примеров  интегралов  ((Приложение A4) приложение №17) с опорой на мультимедийный аппарат.   Используют «матрицу формул». Продолжают A17) учиться применять справочную литературу с опорой на мультимедийный аппарат.	Развито умение выполнять работу самостоятельно ОК4       Осуществлена связь между теоретическими знаниями и практическими умениями. ОК3                     Продолжается связь между теоретическими знаниями и практическими умениями. ОК5   Студенты показывают получение быстрого и правильного результата. ОК4-6
	2.4. Развитие усвоенных знаний	Работать над достижением  прочности знаний.	Вопрос № 3. Практикум по вычислению  интеграла. Организует  выполнение заданий на основе индивидуальной  и фронтальной работы. Контролирует правильность решений. Комментирует ответы, выставляет отметки.	Выполняют  задания индивидуально на доске 4 студента, группа выполняет те же задания. 1.Вычислить предел:                                                      2. Вычислить предел:  (1+5z) = ( (1+5z) ) =e=e=e 3.     ==                                                           =lnx-= 4.  Вычислить  путь, пройденный точкой за 2 с от начала движения, если скорость движения точки изменяется по закону v=(2t+3) м/с.     Решение:                        s=        Ответ:10.	Студенты показывают отличный результат и по пределам и по интегралам. ОК4,5
			Приступает к обсуждению   вопроса №4 семинара «Приложения интеграла»
		Выявить степень осознанности и глубины  знаний по теме. Проверить знания по теме на основе  теста.	Активизируют знания по вопросу № 4 на основе выполнения заданий по приложению 16. Задания в 4 вариантах.                 Приложения интеграла рассматривает по темам:  нахождение площадей фигур и решения задач физического содержания (в вычислении работы силы, пути пройденного точкой, силы давления жидкости и работы производимой при поднятии груза) рассматривается с помощью показа презентацией студентов.	Обсуждают и комментируют формулы в группах. Групповая работа. (Приложение A16)     Студенты (Сергей С., Елена Е.)  рассказывают приложения интеграла  на основе презентаций.  Согруппники делают выводы и рецензию по ходу защиты работ автором.  (Приложения B6,7)     Выполняют  задания в течение 10 минут. Проверяют  правильность решений  с опорой на мультимедийный экран. Самоконтроль.	Ответы: № 1 вариант A-1-3, 2-2, 3-3, 4-4, 5-1. № 4 вариант A-1-4, 2-2, 3-3, 4-4, 5-1. ОК6     Развито умение выполнять работу самостоятельно ОК4
			Проводит устную работу  с опорой на матрицу примеров по теме «Приложения интегралов» с  аргументацией решения (Приложение A5).   Проводит тест  по теме «Интегральное и дифференциальное исчисление» (4 варианта), (Приложение A16)     Музыкальная пауза «Трек-4» по ходу самостоятельной работы. (Приложение D)		Развито умение выполнять работу самостоятельно ОК4
3. Заключительная часть	3.1. Подведение итогов занятия	Дать качественную оценку выполнения семинарского занятия	Оценивает работу группы в целом, отмечая индивидуально наиболее активных студентов, собирает презентации, решения практических заданий для проверки.	Осмысливают свою деятельность на занятии. Сдают подготовленные материалы на проверку.	Подведен итог занятия.
	3.2 Выдача домашнего задания	Сообщить и разъяснить методику выполнения домашнего задания.	Сообщает и объясняет домашнее задание, комментирует задания: решить примеры; подготовиться к зачету (в форме контрольной работы).	Записывают домашнее задание: 1)подготовиться к зачету; 2)решить примеры: а)=? б) функция  в т. х=3 определена? в) S? y = х+12 и у = 16; г) у = arсtg(x-1), dy ?	Группа получила домашнее задание

Краткий самоанализ учебного занятия:

·       В результате занятия обучающиеся  имеют возможность повторить и закрепить изученную ранее тему. Повторение проходит в момент фронтального опроса, закрепление проходит при ответах на вопросы семинарского занятия.

·       Практическое задание выполняется обучающимися самостоятельно, что позволяет им получить опыт самостоятельной работы. Преподаватель консультирует обучающихся при возникновении затруднений.

·       В результате обучающиеся отработают навыки выполнения операций над интегралами и их приложениями.

Преподаватель:      ____________ /Кондратьева Евдокия Андреевна 

Приложения

                                                                 Приложение 4

Приложение 3

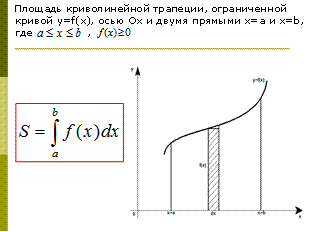
Приложение 6

Приложение 8

                                                             Приложение 9                                      Приложение 10

Приложение 11

Скачано с www.znanio.ru