Конспект урока и презентация на тему "Теорема Пифагора"(8 класс,геометрия)

Урок по геометрии в 8 классе.

Тема: Теорема Пифагора

Составитель:  Латыпова Г.В., учитель математики высшей категории МБОУ СОШ №1 с.Федоровка Федоровского района РБ

Аннотация  к уроку:

         Данный урок является уроком обобщения материала. На нем рассматривается доказательство теоремы Пифагора отличное от рассматриваемого в учебниках. Разбираются практические задачи, при решении которых применяется эта теорема. Рассматривается задача на определение высоты равностороннего треугольника и его площади, полученные формулы используются часто и в геометрических задачах ЕГЭ.

         В целях экономии времени решения задач оформлены на слайдах, но отображаются они частями, по мере их разбора и обоснования.  В конце уроке проводится тест на проверку знаний о площадях четырехугольников, результаты проверяются путем взаимопроверки учащимися работ соседа и выставляются оценки по отображаемой на слайде шкале. Подводится итог урока, и задается домашнее задание.

Цель: - обобщить и систематизировать знания учащихся по теме; познакомить ребят с доказательством Гарфилда теоремы Пифагора; способствовать формированию навыков применения теоремы Пифагора к решению различных задач; вывести формулы площади и высоты равностороннего треугольника; проверить усвоение формул площадей многоугольников и теоремы Пифагора.

- воспитывать интерес к изучению геометрии;

- развивать логическое мышление, память  и навыки устного счета.

Демонстрационный материал: презентация

Ход урока

1.     Орг. Момент

Знакомство с темой урока (Слайд 1).

Постановка целей урока для учащихся (Слайд 2)

2.     Изучение нового материала

- Мы с вами уже знакомы с одним из доказательств Теоремы Пифагора, но их существует более 500. Сегодня мы познакомимся еще с одним, которое предложил Джеймс Гарфилд, будучи преподавателем электического университета (1856-1859 гг), в последствии он стал 20-м президентом США.(Слайд 3) Следует отметить, что доказал он теорему до селе неизвестным способом. Опирался он на  знание формул площадей трапеции и треугольнтка (Слайд 4).

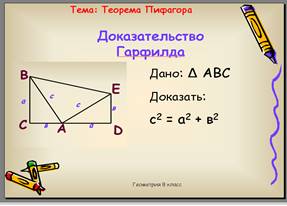
Доказательство предлагает ученик

3.     Решение задач

- Хорошо, а теперь мы переходим к реализации нашей 1 цели. Для этого рассмотрим задачу индийского математика XII в. Бхаскары:

На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота? (Слайд 5)

- составляем чертеж по условию задачи (Слайд 6)

Идет обсуждение решения задачи (фронтально) и записывается ее решение (Слайд 7)

- Переходим к следующей задаче: Вычислите высоту и площадь равностороннего треугольника со стороной а (Слайд 8)

Идет обсуждение решения задачи (фронтально) и записывается ее решение (Слайд 9)

Полученные формулы записываем в справочники.

4.     Проверочная работа – тест (Слайды 10-16) работа оформляется на листочках через копирку, один экземпляр сдается учителю, а другой передается соседу по парте.

1. Выберите верные утверждения:

a)     Площадь прямоугольника равна произведению двух его соседних сторон;

b)    Площадь квадрата равна квадрату его стороны;

c)     Площадь параллелограмма равна удвоенному произведению двух его соседних сторон.

2. Выберите верные утверждения:

a)     Площадь прямоугольника равна произведению двух его соседних сторон;

b)    Площадь квадрата равна квадрату его стороны;

c)     Площадь параллелограмма равна удвоенному произведению двух его соседних сторон.

3. По формуле                  можно

вычислить площадь:

a)     прямоугольника;

b)    параллелограмма;

c)     треугольника.

4. Выберите верное утверждение. Площадь прямоугольного треугольника равна:

a)     половине произведения его стороны на какую-либо высоту;

b)    половине произведения его катетов;

c)     половине произведения гипотенузы и катета.

5. По формуле                     можно

вычислить площадь:

a)     трапеции;

b)    параллелограмма;

c)     треугольника

6. Выберите верное утверждение. В прямоугольном треугольнике:

a)     квадрат гипотенузы равен квадрату суммы его катетов;

b)    квадрат катета равен разности квадратов его гипотенузы и другого катета;

c)     квадрат гипотенузы равен сумме квадратов его катетов.

7. Вычислите площадь самого большого треугольника :

a)     112 кв.ед.;

b)    56 кв.ед.;

c)     144 кв.ед.

Проводится взаимопроверка работ учащимися по ответам Слайд 17

Выставляется оценка учащимися и работа сдается учителю.

5.     Подведение итогов.

Итак мы возвращаемся к началу урока – к его целям.

1.      мы рассмотрели решение задач с применением теоремы Пифагора и вывели формулы для вычисления площади и высоты равностороннего треугольника (Слайд 18)

2.      мы проверили ваши знания

6.     Домашнее задание

Задается домашнее задание по уровням: 1 уровень для всех; 2 уровень для сильных и увлеченных.(Слайд 19)

Спасибо всем. Урок окончен.