Конспект урока на тему "Существование плоскости, проходящей через данную прямую и данную точку"

УРОК 2

Тема. Существование плоскости, проходящей через данную прямую и данную точку

Цель урока: изучение теоремы о существовании плоскости, проходящей через данную прямую и данную точку, которая не лежит на прямой.

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания

1. Фронтальная беседа по контрольным вопросам № 1, 2 §1 из учебника с использованием схемы “Аксиомы стереометрии”.

2. Математический диктант.

Дано изображение тетраэдра SABC (вариант 1 – рис. 8, вариант 2 – рис. 9).

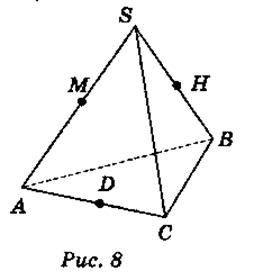
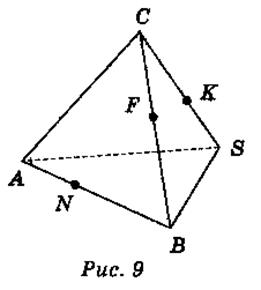
Пользуясь рисунком, запишите:

1) точки, которые принадлежат плоскости грани АВС; (2 балла)

2) точки, которые не лежат в плоскости грани АВС; (2 балла)

3) общие точки плоскостей граней АВС и ABS; (2 балла)

4) прямую пересечения плоскостей граней АВС и SBC; (2 балла)

5) плоскость, которая проходит через прямые АВ и ВС; (2 балла)

6) плоскость, которая не содержит ни одной из прямых АВ и ВС. (2 балла)

3. Решения задач № 1, 3 проверить по записям с пробелами сделанными на доске до начала урока.

Решение задачи № 1

Докажем методом от противного. Допустим, что АВ и СD ..., тогда по аксиоме ... через прямые АВ и CD можно провести ... Итак, точки А, В, С, D лежат в ... плоскости, что противоречит условию. Таким образом, прямые АВ и СD...

Решение задачи № 3

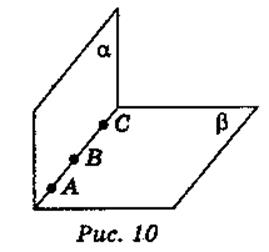
Пусть две различные плоскости α и β имеют общие точки: ... (рис.10). Согласно аксиоме ... плоскости пересекаются ... по ..., которая содержит точки А, В, С.

Следовательно, точки ... лежат на ... пересечения данных ..., то есть на ... прямой.

II. Восприятие и осознание нового материала

Теорема о существование плоскости, проходящей через данную прямую и данную точку

Один способ определения плоскости в пространстве известный (аксиома С3): две прямые, которые пересекаются, определяют в пространстве плоскость, и к тому же только одну.

Второй способ задания плоскости дает теорема:

Через прямую и точку, которая не принадлежит ей, можно провести плоскость, и к тому же только одну.

Пусть АВ – данная прямая и С – точка, которая ей не принадлежит (рис. 11).

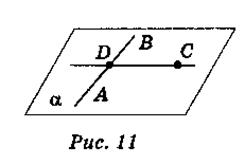
Доказательства (существование плоскости).

Доказательства (единство плоскости).

Докажем от противного. Предположим, что существует две плоскости α и β, которые проходят через прямую АВ и точку С. По аксиоме С2 плоскости α и β пересекаются по прямой, которой принадлежат А, В, С, что противоречит условию. Следовательно, плоскость, проходящая через прямую и точку, не принадлежащую прямой, единственная.

Задачи.

1. Укажите прямую и точку, с помощью которых можно задать плоскость основания куба (см. рис. 2), тетраэдра (см. рис. 3).

2. Дано изображение куба АВСDА1B1С1D1. Какой плоскости принадлежат:

а) прямая АВ и точка D; б) прямая ВВ1 и точка С1; в) прямая АС и точка С1 ?

III. Закрепление и осмысление знаний учащихся

Выполнение упражнений

1. Докажите, что через прямую и точку, лежащую на прямой, можно провести плоскость.

2. Задача № 7 из учебника (с. 9).

3. Прямая а лежит в плоскости α. Докажите, что через прямую а можно провести плоскость β, отличную от α.

4. Даны десять точек, которые не лежат в одной плоскости. Могут девять из них лежать на прямой? Ответ обоснуйте.

5. Можно ли через точку О пересечения двух данных прямых а и b провести третью прямую с, которая не лежит с прямыми а и b в одной плоскости. Ответ обоснуйте.

6. Задача № 4 из учебника (с. 9).

IV. Домашнее задание

§1, п. 2; контрольный вопрос № 3; задача № 6 (с. 9).

V. Подведение итога урока

Вопросы к классу

1) Сколько плоскостей можно провести через прямую а и точку В, которая не принадлежит прямой а?

2) Сколько плоскостей можно провести через прямую а и точку А, которая лежит на прямой а?

3) Через прямую а и точку В можно провести две различные плоскости. Как расположены пряная а и точка B?