Конспект урока по теме «Вычисление площадей криволинейных фигур» (11 класс)

Этапы урока

Деятельность учителя

Деятельность учащихся

Примечания

I. Организационный момент

- Здравствуйте. Сегодня мы с вами повторим материал, который  изучали на прошлых уроках, и познакомимся с новой темой.

На экране слайды

1 слайд. Тема урока

2 слайд. Цели и задачи урока

3 слайд. План урока.

II. Актуализация знаний

1.Устная фронтальная работа по вопросам

2. Устная работа по рисункам

3. Решение упражнений по рисункам на слайдах

4. Самостоятельная работа по вариантам.

III. Физкультминутка

IV. Изучение новой темы

1.Объяснение нового материала

2. Закрепление нового материала.

IV. Разноуровневая самостоятельная работа

V. Домашнее задание

VI. Подведение итогов урока

- Дайте определение первообразной.

- как ещё называется первообразная?

- какие правила  нахождения  первообразной вы знаете?

- Соотнесите строки левого столбца со строками из правого

-Дайте определение криволинейной трапеции

Какие из графиков, изображённых на рисунках,  являются криволинейными трапециями.

Назовите алгоритм нахождения  площади криволинейной трапеции

Вычислите площадь криволинейных фигур

А)

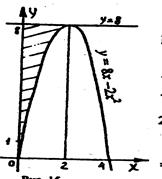
Б)

1 вариант

1)a=                                                                  

b =                                                                    

2)     F(x) =

3)     F(b)=                                 

F(a) =

 4) S = F(b) – F(a

 2 вариант

1)a=                                                                  

b =                                                                   

2)     F(x) =

3)     F(b)=                                 

F(a) =

 4) S = F(b) – F(a)

Нам пора передохнуть, потянуться и вздохнуть (глубокий вдох и выдох).

Для начала мы с тобой, крутим только головой (вращение головой).

Покрутили головой и усталость вся долой;

Прочь прогоним лень и скуку, разомнем сначала руки (выполняются волнообразные движения кистями рук);

Встали дружно. Наклонились

Раз –вперёд, а два – назад.

Потянулись. Распрямились.

Приседаем быстро, ловко-

Здесь видна уже сноровка.

Чтобы мышцы развивать,

Надо много приседать.

Мы на месте снова ходим,

Но от парты не отходим.

По местам пора садиться

И опять начать учиться.

- Отдохнув немного,  снова приступаем к работе.

- Для вычисления  площади криволинейной трапеции можно применить другую формулу

   S =

Сравнивая  формулы

S =                                              S = F(b) – F(a),

делаем вывод

  S=                 =    F(b) – F(a)

Эта формула была открыта одновременно сразу двумя учеными Исааком Ньютоном и Готфридом-Вильгельмом Лейбницем
Поэтому получила двойное название – формула Ньютона-Лейбница. Для удобства запись в правой части принято сокращённо обозначать 

 F(b) – F(a) = F(x) │

Вычислить следующие интегралы

1.       ;  ; 

        2. ;  

3.     

Применив новую формулу, вычислим..

1 группа работает самостоятельно в тетрадях

Задание. Вычислите, (предварительно сделав рисунок) площадь фигуры, ограниченную линиями

 у= х²  - 4х + 5,  у =5

y = 2cos x, y =1, x = -π\3, 

x = π\3

2 группа работает с учителем

1.Вычислите площадь  фигуры, ограниченную линиями y = x² , y = 4, x = -2, x = 2.

2. Вычислите площадь фигуры  у = sin ( x +π\2) 

1. Подготовить сообщение о Ньютоне и Лейбнице ( по желанию).
2. № 357, 358. (1)

 Итак: (рефлексия)

Подведем итоги нашей совместной работы – продолжите мое предложение

Сегодня я узнал новое…

На уроке мне пригодились знания…

Для меня было сложно…

На уроке мне понравилось….

Урок окончен. Спасибо за работу.  До свидания.

- Первообразной функции f(x) называется такая функция F(x), производная которой равна данной функции.

- Неопределённый интеграл

- Три правила.

Правило 1.Если F есть первообразная для f, а G – первообразная для g, то F +G есть первообразная для f + g.

Правило 2. Если F есть первообразная для f, а k – постоянная, то функция kF – первообразная для kf.

Правило 3. Если F(x) есть первообразная для f(x), а  k, b - постоянные, причём k ≠ 0, то    

 F(kx + b) есть первообразная для

F(kx + b).

Фигуру, ограниченную графиком функции, отрезком [а;в] оси Ох и прямыми х = а и х = в, называют криволинейной трапецией.

- а), в)

Алгоритм нахождения  площади криволинейной трапеции
1) Определить пределы интегрирования
       а =   
       b =
2) Найти первообразную функции, ограничивающую криволинейную трапецию
F(x)=
3)  Вычислить значение первообразной в  верхнем пределе F(b), а затем – в нижнем F(a).
4) Найти разность первообразных
S = F(b) – F(a).

К доске выходят 2-е учащихся. Решают задания. Остальные работают в тетрадях.

А) Решение.

1) а =

в =

2) F(x) = -cos x - x +C

3) F() = -cos  -  = =   -
F() = -cos  -  = = -  -
4) S = F(b) – F(a)=  -  - (-  -  =
Ответ.

Б) Решение.

Площадь данной фигуры равна разности площадей

прямоугольника со сторонами 2 и 8  и криволинейной трапеции, ограниченной графиком функции у = 8х – 2х² на отрезке [0;2]

S₂ = 16

S₁ = F(2) – F(0)

F(x) = 4x² -
S₁ = 16 -

S = S₂ – S₁ = 
Ответ.  

Задание выполняется на отдельных листах

Учащиеся выходят из-за парт и выполняют упражнения вместе с учителем.

К доске вызываются учащиеся и решают задания, остальные в тетрадях.

1 группа работает самостоятельно в тетрадях

Задание. Вычислите, (предварительно сделав рисунок) площадь фигуры, ограниченную линиями

 у= х²  - 4х + 5,  у =5

y = 2cos x, y =1, x = -π\3, 

x = π\3

Слайд с вопросами.

После ответов учащихся на вопрос появляется верный ответ.

Слайд с таблицей.

С помощью анимации проводятся стрелки от функций к их первообразным.

На слайде рисунки.

После ответов учащихся

Появляется слайд с верным алгоритмом.

Слайды с рисунками.

Решения и ответы проверяются на слайдах.

Задание выполняется на отдельных листах, проверяем с помощью слайдов.

Формулы появляются на слайдах.

На экране появляются портреты учёных

Работа сопровождается презентацией.