Конспект урока "Практическое применение подобия треугольников "

МКОУ «Рождественско -Хавская СОШ»

Открытый урок

по геометрии в 8-ом классе

«Практическое применение

подобия треугольников»

                                                                                          Подготовила и провела

                                                                                          учитель математики

                                                                                          Ярмонова Вера Васильевна

2016 г.

Тема урока «Практическое применение подобия треугольников»

Дидактическая задача: Формирование универсальный учебных действий  в условии решения практических задач

Цели урока:

Образовательные

·        закрепить признаки подобия треугольников;

·        рассмотреть случаи практического применения подобия треугольников;

Развивающие

·        повышать интерес учащихся к изучению геометрии;

·        активизировать познавательную деятельность учащихся;

·        формировать качества мышления, характерные для математической     деятельности и необходимые для продуктивной жизни в обществе;

·        учиться умению ясно, точно, грамотно излагать мысли, рассуждать, обосновывать способ решения проблемы творческого и поискового характера;

·        учиться слушать и вступать в диалог, участвовать в коллективном обсуждении проблем;

·        формирование коммуникативных навыков групповой деятельности;

Воспитательные

·        мотивировать интерес учащихся к предмету;

·        воспитание математической культуры: владения математическим языком и умений выразить грамотно свою мысль;

 .        воспитание настойчивости в достижении цели.

Тип урока: урок закрепления и применения знаний.

Формы работы учащихся: дискуссия, индивидуальная и фронтальная работа.

Методы обучения: словесные, наглядные, практические.

Оборудование: проектор, ноутбук, раздаточный материал, презентация.

План урока:

1. Организационный момент
2. Мотивация урока

3. Формулировка темы и целей урока
4. Актуализация знаний

5. Применение теоретических основ при решении практических задач
6. Физкультминутка 
7. Закрепление материала. Решение задач
8. Подведение итогов. Рефлексия
9.  Домашнее задание

Ход урока

1. Организационный момент

Добрый день! Добрый час!

Как я рада видеть вас.

Прозвенел уже звонок

Начинается урок.

Улыбнулись. Подровнялись.

Друг на друга поглядели

И тихонько дружно сели.

2. Мотивация урока.

Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:

- Что есть больше всего на свете? – Пространство.

- Что быстрее всего? – Ум.

- Что мудрее всего? – Время.

- Что приятнее всего? – Достичь желаемого.

- Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.

А начну я свой урок с комплимента.

Саша, ты сегодня бесподобен! Как вы думаете, что я имею в виду? Как вы понимаете мои слова? (подобных людей ему нет). А какие фигуры называются подобными?

Слайд

Итак, речь сегодня пойдет о подобии. Какую тему мы изучили? (подобие треугольников).

А применяется ли эта тема в нашей жизни?

Геометрические знания широко применяются в жизни - в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при изготовлении технических чертежей - выполнять геометрические построения; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными  теоремами.

Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.

Мы уже знаем свойства и признаки подобия треугольников. Где могут примениться полученные знания?

-На практике.

Как вы думаете, какова тема нашего урока?

Запишем тему урока: «Практическое применение подобия треугольников»

Давайте сформулируем цель урока.

Послушайте слова  баснописцаА.Н. Крылова

«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».

Итак, цель нашего урока: рассмотреть случаи практического применения подобия треугольников.

На протяжении урока вы будете заполнять индивидуальные карты, там есть таблица. Каждый столбец имеет своё название: что я знаю? что я хочу узнать?  что я узнал? 

3.Актуализация усвоенных знаний учащихся

Давайте ответим на вопрос :  что я знаю?

Ответы: 1) определение подобных треугольников;

              2)первый, второй, третий признак равенства треугольников;

              3)умеем находить подобные треугольники и их сходственные стороны;

              4)умеем составлять пропорции;

              5)решать задачи (устное решение задач по слайду)

Что еще вы хотите узнать на уроке?

-О практическом применении подобия треугольников

Какой вопрос возник в начале урока?

- Как определить высоту дерева, высоту столба?

 Подобные вопросы возникали у людей с давних времен.

 И они могли справиться с такими задачами. Как?

 Сегодня вы сможете ответить на эти вопросы.

.

4.Применение теоретических основ при решении практических задач

А)Задача№1: Определить высоту отдельно стоящего дерева.

С чего же мы начнем решение этой задачи?

Мы имеем отдельно стоящее дерево и солнечную погоду.

Дерево, как и любой предмет, при солнечной погоде отбрасывает тень.

Может кто-то догадался, как решить эту задачу?

Для определения высоты дерева нам понадобится веха (колышек), который мы      должны вбить в землю в вертикальном положении. Веха тоже отбрасывает тень.

В связи, с чем же предметы в солнечную погоду имеют тень? (солнечные лучи). Изобразим их на чертеже. Солнечные лучи можно считать параллельными потому, что расстояние от Земли до Солнца 150 млн. км, а угол между солнечными лучами очень мал.

Мысленно видим два треугольника ABC и MNK.

Что мы можем сказать об этих треугольниках? (Треугольники подобны по первому признаку подобия: <BCA = < NKM,  так как AC||MK и BC||NK, <BAC=<NMK=90^o. Из подобия треугольников следует, что ).

Можем ли мы измерить высоту вехи, длину тени вехи и дерева? (Да)

Тем самым мы можем найти АВ? (Да). Как мы это сделаем?

()

Давайте немного отдохнем. Закроем глаза и представим себе знак подобия. Проведем глазами по контуру этого знака. Повторим эти движения 4 раза.

Пусть высота вехи равна 1 метру, а ее тень 1,9 метра. Длина тени дерева составляет 21 метр. Найти высоту дерева.

Воспользовавшись только что полученной формулой

 определим высоту дерева

(  (м)).

Сейчас мы воспользовались самым легким и древним способом, которым еще греческий мудрец ФАЛЕС за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался её тенью.

 Физкультминутка

Б) Исторический материал

Послушайте внимательно увлекательную легенду.

                                            Легенда

Как это было, рассказывается в книге Я.И. Перельмана "Занимательная геометрия".Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени

ПРИТЧА:

« Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мановению руки распахнулись перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы,

хранители великих тайн природы.

- Кто ты? – спросил верховный жрец.

- Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

- Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на неё? – Жрецы согнулись от хохота.

- Будет хорошо, - насмешливо продолжал жрец, - если ты ошибёшься не более чем на 100 локтей.

- Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта.

- Хорошо, - сказал фараон. – Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».

—  На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.

—  Определение высоты пирамиды по длине ее тени.

— 

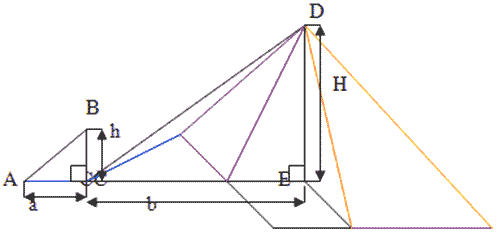
—  Рис. 2

—  ВС - длина палки, DE - высота пирамиды.

—   АВС подобен СDE (по двум углам):

—   ВСА=  СED=90°;

—   АВС=  СDЕ, т. к. соответственные при АВ || DС и секущей АС (солнечные лучи падают параллельно)

—  В подобных треугольниках сходственные стороны пропорциональны:

—  .

—  Таким образом, Фалес нашел высоту пирамиды.

Вот так выглядит модель решения этой задачи.( прокомментировать рисунок) .

Слайд

Но данное решение не всегда можно применить. Почему?

-Скажите, в современном мире есть необходимость измерить высоту большого объекта?

Отв:  Да

- Этими объектами могут быть телеграфные столбы, башни, здания. Способы измерения высоты таких объектов весьма разнообразны.

В) Работа по учебнику

Обратимся к нашему учебнику стр 149 прочитаем Определение  высоты предмета, делая карандашом пометки в тексте, чтобы потом более грамотно сформулировать свои мысли.

Задача№2: Определить высоту предмета в пасмурную погоду.

Работает ученик у доски

Определение высоты дерева по зеркалу  (разбор по слайду)

Также роль зеркала может  играть лужа, ход решения тот же.

Самостоятельная работа(по слайду)

- Я предлагаю решить задачу по готовому чертежу. (по слайду)

Физминутка.(для глаз музыку включить)

У:  сейчас вы решали задачу предложенную мной. Но в жизни часто приходится самостоятельно принимать решения, используя и те знания, которые  получили в школе.

Актуальность этого вопроса заключается в том, что такие задачи включены в практическую часть ОГЭ.

Подведение итогов. Рефлексия.

А теперь давайте закончим с вами предложения:

«Сегодня на уроке я повторил…»

«Сегодня на уроке я узнал…»

«Сегодня на уроке я научился…»

У: Начиная урок, мы поставили цель научиться применять теоретические знания в решении практических задач.

Достигли мы её?

Отв: да

Предлагаю вернуться к таблицам и заполнить её до конца.  Наш урок подходит к концу подведем итог, выразим свое отношение.

Уметь применить в жизни! Можете ли вы сказать: «Сегодня я знаю больше, чем вчера».Если да, то поставьте (+),если нет(!)

Класс! (Здорово!)

Закончили работу. Молодцы. Сдайте  индивидуальные карты. И запишем домашнее задание: П 64, стр 150. ,  №579, творческое задание: подготовить рисунки, макеты подобных фигур.

Оценки за урок

Спасибо за урок.