Конспект урока "Теорема, обратная теореме Пифагора"

В этом уроке мы вспомним теорему Пифагора и познакомимся с обратной ей теоремой. Отметим, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются «пифагоровыми треугольниками». А также поговорим о «египетском треугольнике», который представляет собой треугольник со сторонами 3, 4, 5. При этом, если пропорционально увеличивать стороны такого треугольника, то полученные треугольники, например, со сторонами 6, 8, 10 или 9, 12, 15 и так далее, также будут прямоугольными.

Конспект урока "Теорема, обратная теореме Пифагора"

На предыдущем уроке мы с вами познакомились с теоремой Пифагора, которая звучит следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На этом уроке мы сформулируем и докажем теорему, обратную теореме Пифагора.

Теорема. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный.

Доказательство.

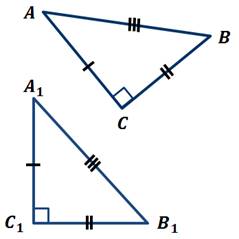
Пусть ABC – треугольник, для которого справедливо равенство: . ,

Докажем, что  – прямой.

 – прямоугольный.

 – прямой, ,.

,

.

Следовательно, ,то есть,.

 по третьему признаку.

Тогда .

Значит,  – прямоугольный.

Что и требовалось доказать.

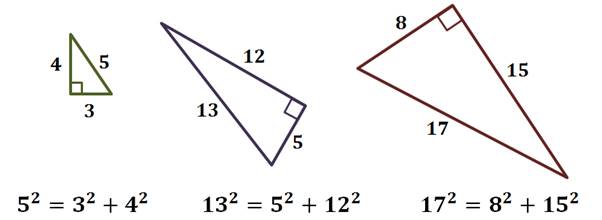
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками. Так каждый из приведённых треугольников является пифагоровым.

В Древнем Египте для построения прямого угла строили прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной три, четыре и пять единиц.

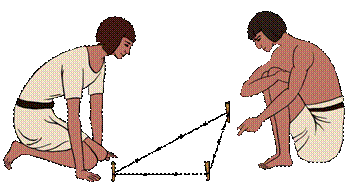
Тогда угол между сторонами, равными трём и четырём, получался прямым.

Задача. Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами: а) , , ; б) , , ; в) , , .

Решение.

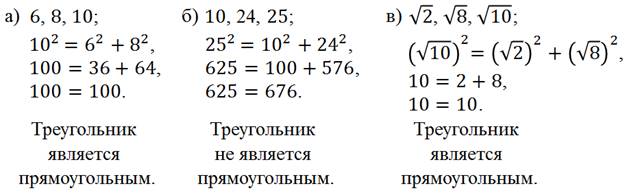
Задача. Найдите площадь треугольника, если его стороны равны  см,  см и  см.

Решение.

, тогда  – прямоугольный, .

,

 (см²).

Ответ:  см².

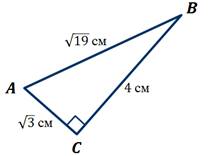
Задача. В равнобедренном треугольнике  длина боковой стороны  равна  см, а основание  –  см. Найдите .

Решение.

 см.

,следовательно,  – прямоугольный, .

Так как  – равнобедренный, то .

,тогда .

Ответ: .

Итак, на этом уроке мы вспомнили теорему Пифагора и познакомились с обратной ей: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный.

Отметили, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.

А также мы поговорили о египетском треугольнике, который представляет собой треугольник со сторонами три, четыре, пять. При этом если пропорционально увеличивать стороны такого треугольника, то полученные треугольники, например, со сторонами шесть, восемь, десять; девять, двенадцать, пятнадцать и так далее также будут прямоугольными.