Основные методические приёмы работы над задачей

Содержание

Введение.............................................................................................................. 3

1. Основные методические приёмы работы над задачей..................................... 4

2. Конкретизация приёмов на примере 1-2 составных задач............................... 6

3.Статьи из журнала "Начальная школа", в которых описан опыт применения различных методических приёмов при обучении решению задач в начальных классах 9

Заключение........................................................................................................ 15

Список использованной литературы................................................................. 16

Введение

Для выполнения каждого приема применяется определенный метод или способ действия, в зависимости от которого выделяют различные виды математических задач: на построение, доказательство, преобразование, комбинаторные, текстовые и т.д.

Текстовая задача - это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий.

Решить задачу – это значит объяснить (рассказать), какие действия нужно выполнить над данными в ней числами, чтобы после вычислений получить число, которое в ней нужно узнать.

Записать решение задачи – значит с помощью цифр и знаков действий показать, что нужно сделать, чтобы найти неизвестное число, выполнить вычисления и дать ответ на вопрос задачи.

Обучение решению задач – это специально организованное взаимодействие учителя и учащихся, цель которого – формирование у учащихся умения решать задачи.

Цель работы: охарактеризовать методические приёмы обучения решению задач в начальных классах.

Задачи:

-охарактеризовать основные методические приёмы работы над задачей.

-конкретизировать названные приёмы на примере 1-2 составных задач.

-подобрать статьи из журнала "Начальная школа", в которых описан опыт применения различных методических приёмов при обучении решению задач в начальных классах.

Структура работы: работа состоит из введения, двух глав, заключения и списка использованной литературы.

1. Основные методические приёмы работы над задачей

Любое умение – это качество человека, а именно: его готовность и возможность успешно осуществлять определенные действия. В методической литературе принято выделять два основных типа умения решать задачи:

Общее умение решать задачи (ОУРЗ) проявляется при решении человеком незнакомой задачи, т.е. задачи такого вида, способ решения которой неизвестен решающему. ОУРЗ складывается из:

· знаний о задачах, структуре задач, процессе решения и этапах решения, методах, способах и приемах решения;

· умений выполнять каждый из этапов решения любым из методов и способов решения, используя любой из приемов, помогающих решению.

Обучение общему умению решать задачи – это

· формирование знаний о задачах, методах и способах решения, приемах, помогающих решению, о процессе решения задачи, этапах этого процесса, назначении и содержании каждого этапа;

· выработка умения расчленять задачи на составные части, использовать различные методы решения, адекватно применять приемы, помогающие понять задачу, составить план решения, выполнить его, проверить решение, умения выполнять каждый из этапов решения [4,с.54].

Умение решать задачи определенных видов состоит из;

· знаний о видах задач, способах решения задач каждого вида;

· умения «узнать» задачу данного вида, выбрать соответствующий ей способ решения и реализовать его на «узнанной» задаче.

Обучение умению решать задачи определенных видов включает в себя усвоение детьми сведений о видах задач, способах решения задач каждого вида (данного вида) и выработку умения выделять задачи соответствующих видов, выбирать способы решения, адекватные виду задачи, применять эти способы к решению конкретных задач [2,с.112].

Этапы обучения младших школьников решению текстовых задач

1. Подготовительный период.

2. Знакомство с текстовой задачей и ее структурой.

3. Решение простых задач на сложение и вычитание.

4. Решение составных задач на сложение и вычитание.

5. Решение простых задач на умножение и деление.

6. Решение составных задач на сложение, вычитание, умножение и деление [1,с.65].

Виды простых задач:

Основа классификации – действие, при помощи которого решается задача: на сложение; на вычитание; на умножение; на деление.

Основа классификации – смысл арифметического действия:

1. Задачи, направленные на раскрытие смысла арифметических действий.

Каждая из этих задач вводится в то время, когда программой предусмотрено ознакомление с соответствующими действиями (сложение, вычитание, умножение, деление).

2. Задачи, раскрывающие различные отношения между числами.

В начальном курсе математики особенно много внимания уделяется работе над отношениями между числами, которые могут быть выражены словами «быть равными», «быть на столько-то больше (меньше), чем», «быть во столько-то раз больше (меньше)» [3,с.14].

Данные задачи могут быть представлены в прямой и косвенной формах:

· В задачах, выраженных в прямой форме, если содержится выражение «на (во) столько-то меньше», т.е. требуется узнать меньшее число, используется действие вычитание (деление); если содержится выражение «на (во) столько – то больше» – сложение (умножение).

· В задачах, выраженных в косвенной форме, при встрече с выражением «на (во) столько-то раз больше», используется действие вычитание (деление), если же содержится выражение «на (во) столько – то раз меньше» – сложение (умножение).

3. Задачи, раскрывающие связи между компонентами и результатами арифметических действий.

Это задачи на нахождение одного из компонентов действия, когда даны другой компонент и результат [2,с.54].

4. Задачи, связанные с понятиями доли, дроби числа.

5. Задачи, в которых раскрывается зависимость между величинами.

Связи между пропорциональными величинами раскрываются с помощью решения простых задач на нахождение одной из величин по данным, соответствующим значениям двух других величин.

Дополнительные задачи: задачи – вопросы, задачи – шутки, задачи на смекалку, задачи с недостающими данными или недостающим вопросом, задачи с лишними данными и т.д.

2. Конкретизация приёмов на примере 1-2 составных задач

Задача: В коробке лежало 3 простых карандаша, а цветных на 2 карандаша больше. Сколько всего карандашей лежало в коробке?

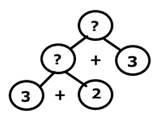
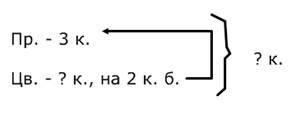
1) 3+2=5 (к.) - цветных карандашей

2) 5+3=8 (к.) - всего карандашей

Ответ: 8 карандашей лежало в коробке.

Задачи с величинами, связанными пропорциональной зависимостью

Это задачи, в которые входят тройки величин, связанных пропорциональной зависимостью (цена, количество, стоимость; скорость, время, расстояние и т.п.).

На нахождение четвертого пропорционального:

Рассматривая математическое содержание задачи на нахождение четвертого пропорционального, необходимо выяснить, какие значения из двух прямо пропорциональных величин даны, значение какой величины требуется найти.

Таблица 1

ВЕЛИЧИНЫ
	цена	количество	стоимость
1	постоянная	даны два значения	дано одно значение, а другое является искомым
2	постоянная	дано одно значение, а другое является искомым	даны два значения
3	даны два значения	постоянное	дано одно значение, а другое является искомым
4	дано одно значение, а другое является искомым	постоянное	даны два значения
5	даны два значения	дано одно значение, а другое является искомым	постоянная
6	дано одно значение, а другое является искомым	даны два значения	постоянная

Способы решения:

1) Способ приведения к единице: сначала узнают значение (цену) единицы одной из пропорциональных величин (товара, работы и пр.), затем значение (стоимость) указанного в условии количества. К единице приводят величину, для которой даны оба значения.

Например, задача: «На 6 одинаковых платьев израсходовали 30 м ткани. Сколько ткани потребуется на изготовление 3 таких платьев?» В задаче известны два значения количества и одно значение общего расхода. При решении способом прямого приведения к единице находим сначала расход на 1 платье: 30:6 =5(м). Затем определяем расход ткани на три одинаковых платья: 5•3=15(м).

2) Способ обратного приведения к единице сводится к нахождению соответствующего значения единицы той величины, для которой в условии указано лишь одно данное (одно значение).

Например, задача: «Для засолки 12 кг огурцов разложили в 6 одинаковых банок. Сколько потребуется таких банок, чтобы разложить 24 кг огурцов?» Учащиеся определяют, сколько раз по 12 кг содержится в 24 кг, т.е. во сколько раз 24 больше 12, значит, и банок получится во столько же раз больше: 6•(24:12)=12 (б.)

Чтобы обеспечить ученику осознанный доказательный выбор арифметического действия, необходимо, прежде всего, улучшить методику организации первичного восприятия и анализа задачи. На первоначальном этапе главное – понять задачу, уяснить, о чём она, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомым. Методика преподавания математики, реализуя цели исторического образования, выработанные государством и обществом и зафиксированные в ФГОС, помогает отобрать содержание образования (в том числе школьных учебников), приспособить это содержание к возрасту и познавательным возможностям учащихся, определить методы и приемы каждого конкретного урока в соответствии с его целями, реализовать задачу познавательного интереса, определить качество образования в процессе выявления результатов преподавания [6,с.54].

Современный урок необходимо рассматривать как звено продуманной системы работы учителя, где решаются задачи обучения, воспитания и развития учащихся.

Новые требования подразумевают, что школьники в процессе обучения должны овладеть УУД, которые формируют у учащихся способность самостоятельно усваивать новые умения и знания. Другими словами, образование по новым стандартам должно развивать самостоятельность у учащихся, формировать способность к самообучению не только по математике, но и по другим школьным предметам.

3. Статьи из журнала "Начальная школа", в которых описан опыт применения различных методических приёмов при обучении решению задач в начальных классах

Таблица 2

Журнал «Начальная школа плюс до и после»

Год	№	Стр.	ФИО	Название	Основные идеи
2013	10	43-47	А.К.Мендыгалиева	Методические приемы при обучении решению задач в начальной школе	В процессе обучения решению задач на уроках математики в начальной школе необходимо использовать специальные задания, включающие сочетания различных методических приемов с целью :научить детей доказывать свою точку зрения, мыслить и рассуждать при анализе условия задачи.
	9	13-16	А.К.Мендыгалиева	Проблемные задания на уроках математики в начальной и основной школе	Проблемные задания на уроках математики учат активно мыслить, самостоятельно формулировать стоящую учебную задачу, доказывать свое мнение. Важное методическое условие-целенаправленное и систематическое использование в ходе учебного процесса проблемных заданий. Выделены основные характеристики проблемных заданий.
	9	35-39	Ж.С.Палладиева	Проблемный урок математики в Образовательной системе «Школа 2100»(2-й класс)	Дается описание уроков по математике по системе «Школа 2100».К познавательной продукции урока относят сформированные представления и знания о математике; к творческой-формулировать определения, делать "открытия", к коммуникативной-умение общаться, в т.ч. и на математическом языке. Здесь же перечислены основные принципы личностно ориентированного обучения по математике.
	10	43-46	Т.В.Баракина	Обучение младших школьников решению составных задач с пропорциональными величинами	Решить задачу-это значит объяснить(рассказать),какие действия нужно выполнить с приведенными числами, чтобы после вычислений получить число, которое нужно узнать. Даны этапы решения составных задач, где в ходе диалога ученик-учитель-ученик обучающийся выходит на правильный результат. Учащийся в ходе диалога развивает свои коммуникативные компетенции, что позволяет ему полюбить предмет «Математика» и не бояться выступать.
2011	2	3-6	О.В.Чиндилова	Разноуровневые задания по освоению младшими школьниками коммуникативных универсальных учебных действий	Освоенные младшими школьниками коммуникативные действия должны быть направлены прежде всего на обеспечение успешной коммуникации. В статье приведен перечень коммуникативных УУД ,который ориентирован на решение задачи, заявленной в стандарте. Здесь же предлагается учителю памятка, с помощью которой он может оценить любое учебное задание и понять, обеспечивает ли оно освоение младшими школьниками коммуникативных учебных действий.
	7	30-33	Н.И.Гажук	Формирование элементов логической и алгоритмической грамотности	Слияние логической и алгоритмической грамотности позволяет создавать условия для формирования ключевых компетенций обучающихся. Алгоритмирование определяет строгую логическую последовательность, непрерывность мыслительной деятельности. Чтобы сформировать логические знания и умения нужно определить, знают ли обучающиеся смысловую характеристику математических терминов, умеют ли задавать вопросы, способны ли в словесной форме описывать таблицы, граф-схемы, блок-схемы. Развитие логического мышления связано с развитием речи, важно, чтобы учащиеся умели объяснять, что они сделали и какой результат получили.
	10	56-59	Е.Д.Сковыро	Применение парной и групповой форм работы на уроках в начальной школе	В статье речь идет о том, что нужно как можно больше выносить заданий на работу в парах, группах. Детей для такой работы нужно готовить. Цель этой работы-развитие мышления, что так необходимо на уроках математики(проверка правильности решения задачи, устного счета, таблицы сложения, умножения, проверка умения правильно задавать вопросы и точно на них отвечать).При работе в парах младшие школьники приучаются внимательно слушать ответ товарища, учатся говорить, отвечать ,доказывать. При работе в группах зажатые дети раскрепощаются, появляется уверенность в собственных силах.
	12	34-36	В.А.Сергеева	Проблемный диалог на уроках математики в начальной школе	В УМК «Школа2100» по математике для проектирования интересных уроков есть все возможности. Автор использует в нем проблемно-диагностическую технологию, которая позволяет преподавание математики превратить в творческий процесс. А творчество начинается с вопросов и поисков ответов на них .Любое продуктивное задание по математике сопровождается текстовой информацией, глубокое понимание которой подразумевает успешное его выполнение.
2010	3	45-47	М.А.Цыварева,Т.И.Назарьина	Формирование у младших школьников вычислительных навыков в условиях сотрудничества	Одной из важнейших задач начального обучения математике по-прежнему остается формирование младших школьников вычислительных навыков .Г.А.Цукерман утверждает, что при совместной деятельности возрастает объем усваиваемого материала, глубина его понимания, растет познавательная активность, творческая самостоятельность. Появляется возможность индивидуализировать обучение, учитывая формирование групп взаимные склонности детей, их уровень подготовки, темп работы и пр., что способствует успешности обучения. Приводится описание групповой работы учащихся на примере уроков, посвященных работе с таблицами с числом 7, где при таком способе сотрудничества процесс освоения материала идет успешнее.
2014	8	17-19	И.И Целищева,С.А.Зайцева	Как научить младшего школьника самостоятельному решению текстовых задач	Авторы статьи утверждают, что каждого школьника можно научить самостоятельно решать задачи. Главное на этапе первичного восприятия и анализа задачи понять задачу, для этого необходимо применять моделирование, при этом уметь пояснять каждое действие .Следует предлагать ученикам и обратные задания. Для формирования умения решать задачи используются: умение ставить вопросы к условию, составлять условие по вопросу, составлять задания по аналогии, составлять задачи по данному решению. При таком подходе у текстовая задача становится более понятной, обеспечивает качественный ее анализ, повышает активность и гибкость мыслительной деятельности учащихся.
Журнал «Начальная школа»
2013	5	56	Л.Н.Годунова	Проект «Создание задачника по математике»	Главным отличием метода проекта является то, что в результате групповой совместной деятельности учащиеся не только получают новые знания, но и создают учебный продукт. Метод позволяет учащимся развивать познавательную активность, творческое мышление, самостоятельно конструировать свои знания, ориентироваться в информационном пространстве.
2014	10	42-46	Е.А.Попова	Работа с таблицами при обучении младших школьников решению задач на процессы	Задачи на процессы считаются одними из самых сложных текстовых задач. Решение их связано с построением таблиц, которая отражает особенности рассматриваемого процесса и отношения между известными и искомыми величинами. Важно использовать различные способы работы с таблицей, направленные на формирование умения вести поиск решения задач на процессы. Авторы предлагают некоторые из них, по которым в результате диалога ученик-учитель-ученик происходит осознание решения данной задачи. Важно научить учащегося рассуждать, говорить, отстаивать свою точку зрения, выстраивать систему доказательства.
2015	10	33-38	А.А.Смирнова	Конструирование исследовательских задач по математике	На сегодняшний день компетентными оказываются те выпускники, которые умеют применять свои знания, умения и навыки в нестандартных ситуациях, гибко перестраивать привычные способы действия, учитывать точки зрения партнеров, конкурентов. Исходя из сути стандарта второго поколения, выпускник начальной школы должен научиться многим универсальным познавательным умениям. Все эти умения можно формировать на уроках математики при использовании метода варьирования текстовых задач.
2015	6	30-34	Н.Б.Истомина, Н.Б.Тихонова.	Развитие универсальных учебных действий у младших школьников в процессе решения логических задач	Решение логических задач на уроках математики создает дидактические условия для овладения младшими школьниками основами логического мышления, математической речи, умения работать с информацией, читать и заполнять таблицы, понимать и составлять высказывания, составлять план, отстаивать свою точку зрения, умение рассуждать.
2016	15	47-49	Л.Ю. Игнатова	Формирование метапредметных и предметных компетенций в ходе решения задач	В статье приводится конспект урока по математике по решению задач. В ходе решения формируются определенные универсальные учебные действия, одними из них являются коммуникативные компетенции: школьники учатся оформлять свою мысль в устной речи, слушать и понимать речь других, работать в команде.
2016	5	55-60	В.С.Овчинникова	Как обучать младших школьников чтению текстовой задачи	Реализация в данной статье методики обучения младших школьников чтению задачи как начальному этапу ее анализа возможна при использовании любых учебников по математике. Главное отличие чтения текстов художественных от математических составляют цель и характерные особенности чтения: рассуждение, умение задавать вопросы, удерживать логическую нить, формирование речевой культуры.
«Начальное образование»
2009	4	11-18	К.И.Щербакова, Л.И.Зайцева	Решение математических задач; опыт, творческие приобретения	В публикации описана экспериментальная методика эффективного обучения старших групп дошкольников решению арифметических задач на основе использования дидактических моделей. Решить задачу- значит раскрыть связи между данным и искомым, ставя правильные вопросы, раскрывая смысл задачи.
2016	5	19-25	Т.Ю.Студенова	Психолого-педагогические проблемы обучения детей решению задач в процессе текстового моделирования	Статья посвящена проблеме устранения психологических трудностей младших школьников при решении математических задач на основе текстового моделирования .Рассмотрен дифференцированный подход к тексту задачи, который помогает более четкому его пониманию в процессе перевода с разговорного языка через мктаязык на математический.

Заключение

Вопросы формирования умений решать текстовые задачи у младших школьников в процессе обучения исследовались в последние десятилетия многими крупнейшими психологами, дидактами, методистами (А. К. Маркова, Л. И. Божович).

Большие возможности для формирования умения у младших школьников создает умение решать задачи.

Сложность материала по математике постепенно возрастает, и в 3-4 классах дети встречаются уже с довольно сложными заданиями, при изучении которых особенно труден для учащихся процесс обучения.

Результаты многолетних теоретических исследований и экспериментов известных отечественных ученых обобщены и претворены в конкретные практические дела: созданы альтернативные программы, учебники и методики, дающие учителю возможность выбора той системы обучения математике, которая поможет ему добиться высокого уровня знаний своих учеников.

Систематическое наблюдение за работой учащихся свидетельствует о том, что текстовые задачи вызывают наибольшие трудности.

Навык решения у детей сформирован недостаточно. Учащиеся нередко не умеют выделить главное, установить связи между понятиями, составить решение., выполнить проверку полученного результата.

Одной из причин такого положения является то, что традиционная практика обучения учащихся решению задач, которая не способствует в должной мере осознанному формированию вычислительных умений у учащихся. Зачастую это сводится к показу образца и разучиванию способа решения. При этом основное внимание направлено на реализацию единственной цели – получению ответа на вопрос задания.

Список использованной литературы

1. Асмолов А.Г., Как проектировать универсальные учебные действия. От действия к мысли / А.Г. Асмолов. – М., 2008. Режим доступа: [http://www.twirpx.com/file/335335/].

2. Асмолов А.Г., Психология личности: культурно-историческое понимание развития человека / А.Г. Асмолов. – М., 2017.

3. Асмолов А.Г., Стратегия социокультурной модернизации образования: на пути к преодолению кризиса идентичности и построению гражданского общества/А.Г. Асмолов// Вопросы образования. – 2015. - № 3.

4. Байрамукова, П.У. Методика обучения математике в начальных классах [Текст]: курс лекций / П.У. Байрамукова, А.У. Уртенова. – Ростов-на-Дону : Феникс, 2012. – 299 с.

5. Белошистая, А.В. Методика обучения математике в начальной школе [Текст]: учеб. пособие для студентов вузов, обучающихся по спец. «Педагогика и методика начального образования» / А.В. Белошистая. – М. : Гуманитар. изд. центр ВЛАДОС, 2011. – 455 с.

6. Гурбатова, Е.Р. Роль допонятийных форм мышления в обучении детей математике [Текст] / Е.Р. Гурбатова // Педагогика. 2014. – № 6.

7. Демидова, Т.Е. Текстовые задачи и методы их решения [Текст] / Т.Е. Демидова, А.П. Тонких. – М.: Изд-во МГУ, 2015

8. Возрастно-психологический подход в консультировании детей и подростков. – М., 2017.

9. Выготский Л.С., Собр. соч. / Л.С. Выготский. – М., 2012. - Т. 4.

10. Гальперин П.Я. Методы обучения и умственное развитие ребенка / П.Я. Гальперин. – М., 2015.

11. Горленко Н.М. Структура универсальных учебных действий и условия их формирования // Народное образование. – 2012. – №4. Режим доступа: [balaxta.ru/biblioteka/gor_1.doc]

Скачано с www.znanio.ru

Содержание Введение ........