Поделиться
kontr._i_samost._rab._po_algebre_7kl._k_mordkovichu_popov_m.a_2011_-64s.pdf
|
|
|
о |
по новому образовательному стандарту УТЛ]
(второго поколения)
М.А. попов
Контрольные
и самостоятельные роботы по алгебре
К учебнику А.Г. МорДковича «Алгебра. 7 класс»
• Разноуровневые задания
•
38 самостоятельных
работ в двух 
вариантах
• 8 контрольных работ в четырех
вариантах
• Ответы
класс
класс
ЭКЗАМЕН
Учебно-методический комплект
М.А. попов Контрольные и самостоятельные работы по алгебре
К учебнику А.Г. Мордковича 
«Алгебра. 7 класс» (М.: Мнемозина)
класс
Рекомендовано 
Российской АкаДемией Образования
ИзДание пятое, переработанное и Дополненное 
Издательство
«ЭКЗАМЕН»
МОСКВА 2011
удк 372.8:512
ББК 74.262.21я72
[158
Имя автора и название шатируемого издания указаны на титульном листе данной ю-ити (ст. 1274 п. части четвертой Гражданского кодекса Российской Федерации).
Изобрджения учебных изданий «Алгебра.
7 о.: в двух частях. Ч 1: учебник для общеобразоват. учреждений / А.Г.
Мордкович. — М.: Мнемозина» и «Алгебра. 7 кл. Ч. 2: задачник для общеобразоват.
учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. 
М.: Мнемозина» приведены на обложке данного издания исключительно в качестве иллюстративного материала (ст. 1274 п. части четвертой Гражданского кодекса Российской Федерации).
попов, МА.
П58 Контрольные и самостоятельные работы по алгебре: 7 класс: к учебнику А.Г. Мордковича «Алгебра. 7 класс» / М.А. Попов. — 5-е изд., перераб. и доп. — М.: Издательство «Экзамен», 201 1. 62, [2] с. (Серия «Учебно-мегодический
комплект»)
ISBN 978-5-377-04163-4
Данное пособие полностью соответствует новому образовательному стандарту (второго поколения).
Пособие является необходимым дополнением к школьному учебнику А.Г. Мордковича «Алгебра. 7 масс», рекомендованному Министерством образования и науки Российской Федерации и ВКЛЮЧеННО• му в Федеральный перечень учебников.
Пособие включает материалы для контроля и оценки качества подготовки учащихся по алгебре и непосредственно должно быть использовано при работе с учебником А.Г. Мордковича «Алгебра. 7 класс».
Представлены 38 самостоятельных работ, каждая в двух вариантах, так что при необходимости можно проверить полноту знаний учащихся после любой пройденной темы; 8 контрольных работ приведены в четырех вариантах, что дает возможность максимально точно оценить знания каждого ученика.
Пособие адресовано учителям, будет полезно учащимся при подготовке к урокам, контрольным и самостоятельным работам.
Приказом 729 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных учреждениях.
удк 372.8:512
ББК 74.262.21я72
Подписано в печать с диапозитивов 17. I I .2010. Формат 84х108/32.
Гарнитура «Таймс». Бумага газетная. Уч.-изд. л. l,2l.
Усл. печ. л. 3,36. Тираж 150 000 (5-й завод — 8000) экз. Заказ № 10631(2)
њврч 978-5-377-04163-4 ©
попов м.А.,
© Издательство «ЭКЗАМЕН», 2011
ОГЛАВЛЕНИЕ
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
К главе 1. Математический язык. Математическая
модель..
Самостоятельная работа № 1. Числовые и
алгебраические выражения
Самостоятельная работа № 2.
Что такое математический язык.
Что такое математическая модель .
Самостоятельная работа № З.
Линейное уравнение с одной
переменной ...............................9 Саиостоятетьная работа № 4.
Координатная прямая 
К главе 2. Линейная функция 
Самостоятельная
работа № 5.
Координатная плоскость
Самостоятельная работа № б. Линейное уравнение с
двумя переменными и его график 
Самостоятельная работа № 7.
Линейная функция и ее график ....
Самостоятельная работа № 8.
Линейная функция и ее график.
.12 Самостоятельная работа № 9.
Линейная функция у = Ь.
Взаимное расположение графиков
линейных функций .
.13 К главе З. Системы двух линейных
уравнений с двумя переменными.
14 Самостоятельная работа № 10. Основные
понятия. Метод подстановки
Самостоятельная работа № 11.
Метод алгебраического сложения
15
Самостоятельная работа № 12. Системы двух линейных
уравнений с двумя переменными как математические модели реальных ситуаций.
16
К главе 4. Степень с натуральным показателем и ее
свойства .
. 17 Самостоятельная работа № 13.
Что такое степень с натуральным показателем
.17
Самостоятельная работа № 14.
Таблица основных степеней.................. . . ...
Самостоятельная работа № 15.
Свойства степени с натуральным показателем .
. 19
Самостоятельная работа № 16. Умножение и деление степеней с одинаковыми
показателями
20 Самостоятельная работа № 17
Степень с нулевым показателем
20
К главе 5. Одночлены. Арифметические операции над
одночленами
21 Саиостоятельная работа М М. Понятие одночлена. Стандартный вид
одночлена
21 Самостоятельная работа № 19.
Сложение и вычитание одночленов .......................................22
Самостоятельная работа № 20.
Умножение одночленов.
Возведение одночлена в натуральную степень
23 Самостоятельная работа № 21.
Деление одночлена на одночлен
23 К главе 6. Многочлены.
Арифметические операции над многочленами .............
.24 Самостоятельная работа № 22.
Основные понятия .
.24 Самостоятельная работа № 23.
Сложение и вычитание многочленов
...24
Самостоятельная работа № 24. Умножение многочлена на одночлен . . ... ...
..................25 Самостоятельная работа № 25.
Умножение многочлена на многочлен
.25
Самостоятельная работа № 26.
Формулы сокращенного умножения ............................ . .... .26 Самостоятельная работа № 27.
Формулы сокращенного умножения .
.26
Самостоятельная работа № 28.
Деление многочлена на одночлен
.27 К главе 7.
Разложение многочлена на множители
28
Самостоятельная работа № 29.
Что такое разложение многочлена на множители и зачем
оно нужно
.28
Самостоятельная работа № 30.
Вынесение общего множителя за скобки....
28
Самостоятельная работа ЛФ З 1. Способ группировки
29
Самостоятельная работа М 32.
Разложение многочленов на множители с помощью формул
сокращенного умножения
29 Самостоятельная работа № 33. Разложение
многочленов на множители с помощью комбинации различных приемов .
Самостоятельная работа М 34.
Сокращение алгебраических дробей .
Самостоятельная работа № 35.
Тождества
К главе 8. Функция у = х
32 
Самостоятельная работа № 36.
Функция у х2 и ее тафик
32 Самостоятельная работа М З 7.
Графическое решение уравнений
32
Самостоятельная работа № 38.
Что означает в математике запись у =Лх)
33
КОНТРОЛЬНЫЕ РАБОТЫ
34Контрольная работа № 1. Числовые и
алгебраические выражения. Что такое математический язык. Что такое
математическая модель. Линейное уравнение с одной переменной. Координатная
прямая
34
36Контрольная работа № 2. Координатная плоскость.
Линейное уравнение с двумя переменными и его график. Линейная функция и ее
график. Линейная функция у = Ь. Взаимное расположение графиков линейных функций
.
.36
К главе З
38
Контрольная работа № З. Основные понятия.
Метод подстановки.
Метод алгебраического сложения. Системы двух линейных уравнений с двумя
переменными как математические модели реальных ситуаций...38
К главе 4
Контрольная работа №
4. Что такое степень с натуральным показателем. Таблица основных степеней.
Свойства степени с натуральным показателем. Умножение и деление степеней с
одинаковыми показателями. Степень с нулевым показателем40 К главе 5
Контрольная работа № 5. Понятие одночлена.
Стандартный вид одночлена. Сложение и вычитание одночленов. Умножение
одночленов. Возведение одночлена в натуральную степень. Деление одночлена на
одночлен
.42
.44Контрольная работа № 6. Основные понятия. Сложение
и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена
. на многочлен. Формулы сокращенного умножения. Деление многочлена на одночлен
К главе 7 ...
46 Контрольная работа № 7. Что такое
разложение многочленов на множители и зачем оно нужно. Вынесение общего
множителя за скобки. Способ группировки. Разложение многочленов на множители с
помощью формул сокращенного умножения. Разложение многочленов на множители с
помощью комбинации различных приемов. Сокращение алгебраических дробей.
Тождества .
46 К главе 8....
.48
Контрольная работа № 8. Функция у =
х2 и ее график. Графическое решение уравнений. Что означает в
математике запись у =Лх)
.48 ОТВЕТЫ .
.50
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Самостоятельная работа № 2.
Что такое математический язык.
Что такое математическая модель
Вариант 1
1. Запишите на математическом языке:
а) сумму чисел х и у.
б) произведение числах и разности чисел 2у и z.
2. Перейдите к математической модели:
а) число а больше числа Ь на число с;
б) частное от деления
а на сумму чисел а и Ь в два раза больше произведения чисел а и Ь.
З. Составьте математическую модель следующей ситуации:
В первом мешке х кг картошки, а во втором — у кг. Если из первого мешка переложить во второй 2 кг картошки, то во втором мешке окажется в два раза больше килограммов картошки, чем в первом.
Вариант 2
1. Запишите на математическом языке:
а) разность чисел х и у.
б) частное от деления числа х на произведение чисел у и :
2. Перейдите к математической модели:
а) число а меньше числа Ь на число с;
б) произведение числа а на разность чисел Ь и с на 5 меньше суммы чисел Ь и с.
З. Составьте математическую модель следующей ситуации:
В первом доме проживает х человек, во втором — на 10 человек больше. Если переселить из первого дома во второй 20 человек, то в первом доме станет проживать в два раза меньше человек, чем во втором.
8
М З.
Линейное уравнение с одной переменной
Вариант 1
1. Решить
уравнение 3х—7 = 5 х +4 
2
2. Решить
уравнение
5 2
З. Пешеход проходит путь из города А в город В за 5 часов. Если бы он шел со скоростью на I км/ч быстрее, то он затратил бы на этот же путь 4 часа. Найдите скорость пешехода.
Вариант 2
4
1. Решить
уравнение 2х+4 = — х 3 
З
2z-l 32+3
2. Решить
уравнение
4 5
З. Автомобиль проезжает путь из города А в город В за 4 часа. Если бы он ехал со скоростью на 20 км/ч быстрее, то он затратил бы на этот же путь 3 часа. Найдите скорость автомобиля.
Самостоятельная работа № 4.
Координатная прямая
Вариант 1
1. Изобразите на координатной прямой точки В(—2,5); 44,5); Ц-О,5).
2, Изобразите на координатной прямой промежуток:
З. Сколько натуральных чисел принадлежкг промежутку [—124; 8)?
Вариант 2
1. Изобразите на координатной прямой точки АН); В(6,5); се,5)•,
2. Изобразите на координатной прямой промежуток:
З. Сколько натуральных чисел принадлежит промежутку (_214; 7]?
9
х К главе 2. Линейная функция
Самостоятельная работа № 5.
Координатная плоскость
Вариант 1
1. Ответьте без построения: в какой координатной четверти расположена точка
а) НО, -7); 
2. На координатной плоскости ХОУ постройте точки А(4; 8) и В(—З; —2) и соедините их прямой.
З. Постройте четырехугольник ABCD, если заданы координаты его вершин: А(—З; -6); В(—З; 4); С(—4; 5); D(6; 7).
Вариант 2
1. Ответьте без построения: в какой координатной четверти расположена точка
2. На координатной плоскости ХОУ постройте точки А(2; -3) и В(—4; 5) и соедините их прямой.
З. Постройте четырехугольник ABCD, если заданы координаты его вершин: А(—З; —5); В(4; —4); С(5; 6); D(—3; 2).
Самостоятельная работа № б,
Линейное уравнение с двумя переменными и его график
Вариант 1 1
1. Постройте график уравнения: 3х-у+2 = 0.
2. Найдите точку пересечения прямых: х+2у = 3 и х-4у = 5.
З. Постройте график уравнения: 2х+у—5 0 и найдите ординату точки с абсциссой 3.
Вариант 2
1. Постройте график уравнения: 2х—5у—3 = 0.
2. Найдите точку пересечения прямых: 2х—у = О и х—3у = 4
З. Постройте график уравнения: 3х+2у = 4 и найдите абсциссу точки с ординатой 5.
7.
Линейная
функция и ее график
1. Преобразуйте линейное уравнение с двумя переменными к виду линейной функции у = Ь+т и найдите К и т: 6) 2х+ЗН = О.
2. Найдите значение линейной функции при заданном значе-
б) у = —2х+4 при х = 2.
2
З. Постройте график линейной функции: у = .
З
1. Преобразуйте линейное уравнение с двумя переменными к виду линейной функции у Кх+т и найдите К и т: 6) 2х-0+8 = о.
2. Найдите значение линейной функции при заданном значе-
2— , б) у = 5—2х при х = 0,2.
З
З. Постройте график линейной функции: у = З— х .
х
8.
Линейная функция и ее график
Вариант 1
1. Найдите значение аргумента, при котором линейная функция у = 2,5—3х принимает значение:
а) -0,5; 6) -15,5.
2. Найдите точку пересечения графиков линейных функций: у = х-2 3-2х.
З. Найдите наименьшее и наибольшее
значения линейной функции У = -4х+3 на заданном промежутке [1 : З]
Вариант 2
1.
Найдите значение аргумента, при котором линейная функция у =
4—2,5х принимает значение: 
6) -8,5.
2. Найдите точку пересечения графиков линейных функций: у = 3—3х иу = х+7.
З. Найдите наименьшее и
наибольшее значения линейной функции у = —2х+1 на заданном промежутке [—1; 1]
1
9.
Линейная функция у = К.х.
Взаимное расположение
графиков линейных функций
Вариант 1
1. Постройте график прямой пропорциональности:
а) у = 2х; б) у = —4х.
2. Установите взаимное расположение графиков линейных функций, не выполняя построений:
а) у = —3х и у = —3х+ 14; б) у = 4х иу = Ах.
З. Найдите наименьшее и наибольшее значения линейной
2
функции у = ——х на промежутке [—330; +00) .
1.
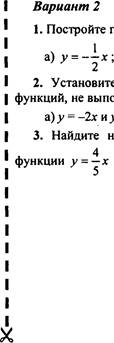Постройте график прямой пропорциональности:
б) у = бх.
2. Установите взаимное расположение графиков линейных функций, не выполняя построений:
а)
у = —2х и у = 2х+3; 
З. Найдите наименьшее и наибольшее значения линейной функции у =—х на
промежутке (—с, —550] 
К главе З. Системы двух линейных
уравнений с двумя переменными
Самостоятельная работа № 10.
Основные понятия. Метод подстановки
Вариант 
1. Является ли решением системы уравнений:
2Х+У = З,
пара чисел:
2.
 |
2х-У=З,
З. Решите систему уравнений:
x-y= l, х У 2х— у
Вариант [1]
1. Является ли решением системы уравнений:
пара чисел:
№ 11.
Метод алгебраического сложения
Вариант 1
1. Решите методом алгебраического сложения систему уравнений:
2x-3y=l, а)6)
У-4х=2.
2. Решите систему уравнений:
4х-9=8.
Вариант 2
1. Решите методом алгебраического сложения систему уравнений:
а)6)
2х+у =2•, -2хч-у=З.
2. Решите систему уравнений:
2х+Зу=5,
12.
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций
Вариант
1. Если к числителю дроби прибавить 1 , а к знаменателю 2, то дробь не изменится. Если же к числителю дроби прибавить 2, а из знаменателя вычесть 1, то дробь увеличится в 6 раз. Найдите эту дробь.
2. Сумма цифр двузначного числа равна 9. Если это число разделить на разность его цифр, то получится 54. Найдите исходное число.
Вариант 2
1. Если к числителю дроби прибавить 2, а к знаменателю дроби прибавить 3, то получится —. Числитель дроби в 3 раза мень-
ше знаменателя. Найдите исходную дробь.
2.
Разность цифр двузначного числа равна 6. Если это число разделить
на сумму его цифр, то получится 8,2. Найдите исход- 
ное число. 
К главе 4. Степень с натуральным
показателем
2-10631
14.
Таблица основных степеней
1
1. Вычислите:
а) (-l)7+l 3
б) (—l )2+0 3+1 5 .
2. Запишите число 312857 в виде суммы разрядных слагаемых.
З. Не производя вычислений, расположите в порядке возрастания числа:
Вариант 2
1. Вычислите:
а) (—l )4
+1 2
2. Запишите число 2237453 виде суммы разрядных слагаемых.
З. Не производя вычислений, расположите в порядке убывания числа:
(-l)5
•, (-3)2 •, (-2)2
15.
х
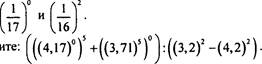16. Умножение и деление степеней с
одинаковыми показателями
1
1. Представьте выражение в виде произведения степеней:
а) (За)5 ; б) (5a2 bc 3 )3 .
2. Найдите
значение выражения 
2119 
(Х5 : Х89
З. Решите уравнение:
Вариант 2
1. Представьте выражение в виде степени произведения:
а) 498; 6) 125ab 6 12 с18
2. Найдите
значение выражения
2 8 . 13 l8
З. Решите уравнение: 
201 .
Самостоятельная работа № 17.
Степень с нулевым показателем
Вариант 1
1, Вычислите:
а) 2 2 +3 3.-5 0 •, 6) 3 0.2 2-4 3 .
2. Сравните значения выражений и результат запишите в виде
неравенства:
З. Вычислите:
Вариант 2
1. Вычислите:
а) 3 2 +42-1 80 б) 20• 3 2+43 .
2. Сравните значения выражений и результаты запишите в виде неравенства:
36 2
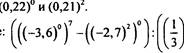З. Вычислите:1
7
К главе 5. ОДНОЧЛИЫ.
Арифметические операции над одночленами
Самостоятельная работа М 18.
Понятие одночлена. Стандартный вид одночлена
Вариант 1
1. Является ли данное выражение одночленом:
а) 2x2 +y7z9
6) за2 ьз
2. Найдите значение одночлена: —a2 b 3 при а = 2— , b = l.
З. Приведите одночлен 2, la 2 b 2 c 4 • —1— •(bc 3 d) к стандартному виду и укажите его коэффициент.
Вариант 2
1. Является ли данное выражение одночленом:
6) з,7аь8.
2. Найдите значение одночлена: 0,2a3 b4 при а = 5; Ь .
З. Приведите
одночлен 0,35abc
•(b 2 c3 d 4 )
к стан
Дартному виду и укажите его коэффициент.
|
а) ху |
2ху; |
|
3,7х уж, |
|
б) х4у5 |
—х5у4; |
—2х у |
3,5х у |
19.
Сложение и вычитание одночленов
1
1. Среди данных одночленов найдите подобные:
а) ху; 2ху; х2у2 ;
—— ху
б) х2уз ; —хзу2 ; 4х2уз , —0,75х2уЗ .
2. Выполните действия:
а) 2, 1х4-1 ,5x4 .
б) —ab3 +—ab 3 .
З. Упростите выражение:
2,5х2ухЗуЗ — I , 5х у4 — х4у5 + 2х4у5 + 4х5у4 .
Вариант 2
1. Среди данных одночленов найдите подобные:
2. Выполните действия:
б) —a 2 b 3 +—a 2 b3
З. Упростите выражение:
3,6хуху2хЗ—2,7х уЗхЗ +х5у —4ху—2х у2у.
х
№ 20,
Умножение одночленов.
Возведение одночлена в натуральную степень
Вариант 1
1. Выполните умножение:
а)
5c7b; 
2. Возведите одночлен —2a2 b3 c в шестую степень.
З. Упростите выражение: 2—a 2
b • ——abc • (—4ab2 )2 . 49
Вариант 2
1. Выполните умножение:
а) (—3а)•4Ь; 
2. Возведите одночлен —3abc в пятую степень. 2 2
2
З. Упростите выражение: 4—abc • ——ас • (-3Ь З с 2 ) 2 .
9
Самостоятельная работа № 21.
Деление одночлена на одночлен
Вариант 1
1. Выполните деление:
а) a21 :a 13 •
2. Какой одночлен необходимо поставить вместо знака , чтобы равенство было верным: = 3a4b2 c? (2a2 b 3 ) 4 • (—3ab) 2 З. Упростите выражение:
(6ab3
Вариант 2
1. Выполните
деление: 32 18. 
2.
Какой одночлен необходимо поставить вместо знака * , чтобы
равенство было верным: (—34а 7 Ь 4 с 19 ). = 2 а bc 
(3a 2 bc)
2 •(—4a3 b 2 ) 3 З. Упростите
выражение:
—8a5b3c
х
К главе 6. Многочлены. Арифметические операции над многочленами
Самостоятельная работа М 22. Основные понятия
Вариант 1
1.Приведите многочлен 3х4—5х 
к
стандартному виду.
2.Найдите значение многочлена, приведя его к
стандартному виду: 
при х = 2, у = —1 .
З. Приведите многочлен к стандартному виду и запишите его члены в порядке убывания степени переменной:
Вариант 2
1. Приведите многочлен 5у—6у2—7у +3y—2y2+y4+l ly3 к стандартному виду.
2.
Найдите значение многочлена, приведя его к стандартному виду: ху 
при
х = 2, у = 1.
З. Приведите многочлен к
стандартному виду и запишите его члены в порядке убывания степени переменной: 
17т+4пР—32+
14m.
Самостоятельная работа № 23.
Сложение и вычитание многочленов
Вариант 1
1. Найдите р(х) = 
если
= х2—4х—3; Р2(х) = х3+4х.
2. Решите уравнение: (3х-4)—(2х+5) = 4х—14+(3х—2).
З. Найдите р(х) =
= 2xy—xz+3yz; )
= XY—XZ+YZ.
Вариант 2
1. Найдите
р(х) = 
если = х—8; Р2(х)
2. Решите уравнение: ч2х+3) = 6х44х—8). 1 З. Найдите р(х) =
= xy+4xz+3yz; =
И.
М 24.
Умножение
многочлена на одночлен
Вариант 1
1. Выполните умножение:
а) (х—2)3х; б)
(х—у+ху)ху. 
1—х
2. Решите
уравнение:
2 З. Выполните действия:
2 аз —4а+2 а4 -28 +2
21a •
7
Вариант 2
1. Выполните умножение:
а) (4—х)2х; 
3-2х
2. Решите
уравнение: 
2 а — 2аз 6
2а—4 З. Выполните действия: 4а• -За 
2 6
Самостоятельная работа М 25.
1 Умножение многочлена на многочлен
Вариант 1
1. Выполните действия:
2.
Найдите
значение выражения: Ха-3) при а = 3. 1 З. Решите уравнение: (2х—4)(6х+3)
Вариант 2
1. Выполните действия:
2. Найдите значение выражения: (а+4)(2—а2Н3а+4)(4—а) при а = 2.
З. Решите уравнение: (4х—3)(2—х) = (—2х+3)(3+2х).
Самостоятельная работа № 26. Формулы
сокращенного умножения
Вариант 1
1. Раскройте скобки:
а) (х+3)2 ,
2. Используя формулу (a+b)(a—b) = 8—b2, выполните умножение:
а) 394 е, б) 46-54.
З. Решите уравнение: 2(х—2)(х+2) —— 
)(х+З)+х.
Вариант 2
1. Раскройте скобки:
а) (х+2)2 ,
2. Используя формулу (a+b)(a—b) = a2—b2 , выполните:
а) 28•32•, 6) 6773.
З. Решите уравнение: 3(x+l = 2(х—2)(х+2)+х2+2х.
Самостоятельная работа № 27. Формулы сокращенного умножения
Вариант 1
1. Раскройте скобки:
6) (-48+0,502 .
2. Выполните умножение: (х+5)(х2—5х+25). З. Найдите значение выражения:
при х = -0 5
Вариант 2
1. Раскройте скобки:
а) (5х2+У2)2; 6) (-38+2,502 .
2. Выполните умножение: (х—6)(х2+6х+36).
З. Найдите значение выражения:
при х = 
№ 28.
Деление многочлена на одночлен
З. Замените знак * одночленом так, чтобы выполнялось равенство:
= 17b3 c 5 —12ab .
З. Замените знак * одночленом так, чтобы выполнялось равенство:
78 -8аЬ 2 с 2 
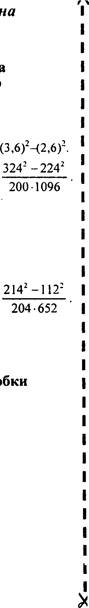
К главе 7. Разложение многочлена на
множители
Самостоятельная работа 29.
Что такое разложение многочлена на множители и зачем оно нужно
Вариант 1
1. Решите уравнение: (3х+4)(х—2) = 0.
2. Вычислите наиболее рациональным способом:
З. Вычислите наиболее рациональным способом•
Вариант 2
1. Решите уравнение: (2х+6)(х—4) = 0.
2. Вычислите наиболее рациональным способом:
2
З— 1- 
2 2
З. Вычислите наиболее рациональным способом.
Самостоятельная работа М 30.
Вынесение общего множителя за скобки
Вариант 1
1. Разложите на множители:
а) 3x+12y•, 6) 2а5 +а3 .
2. Решите уравнение: 2х2—8х = 0.
З. Разложите на множители: 3x2y5z+
12xy2z—4x 2 3у 
Вариант 2
1. Разложите на множители:
2
а) 4х+ I бу; б) за+а.
2. Решите уравнение: 3х2 +7х = О.
З. Разложите на множители: 2xyz—3x2z2+4xy3z.
М 31.
2
при х 
З
при х 2,
33. х
Разложение многочленов на множители с
помощью комбинации различных приемов
Вариант 1
42 .
1. Разложите на множители: а) 3-278, 6) 16b-b
2. Разложите на множители, используя метод выделения полного квадрата двучлена: х2— 12х+32.
З. Решите уравнение: 2х3 +4х2 = 8(х+2).
Вариант 2
2 53 .
1. Разложите на множители: а) ба б) 9b—b
2. Разложите на множители, используя метод представления одного из членов многочлена в виде суммы двух подобных сла-
2
гаемых: х+5х-4.
32 = 12х+24. З. Решите уравнение: 3х+6х
Самостоятельная работа № 34.
Сокращение алгебраических дробей
Вариант 1
3
1. Сократите дробь: а) 6) х1
2. 
Найдите
значение алгебраической дроби, предварительно
3а2 — 6ab + 3b2
сократив ее: при
4(а — + Ь)
32a 2 b3 c+ 16a 2 bc —24a3 b 2 c З. Сократите дробь:
8a(4ab2 3a2b) 1
Вариант 2
5
1. Сократите
дробь: 
6)
2. 
Найдите
значение алгебраической дроби, предварительно 2аз +28 сократив
ее: при а = 2; Ь = 3.
6х 2 у 2 —24х3
уЗ З. Сократите дробь: 
з 
(l — 4») • ху
35.
Тождества
1. Являются ли данные выражения тождествами:
2 22
= b2 .
З. Является ли данное выражение тождеством при допусти-
—4х ?
1. Являются ли данные выражения тождествами:
6)
(а-Ь)2 +4аЬ = (a+b)2? 
= 8ab.
З. Является ли данное выражение тождеством при допусти-
6х2
2х2
х К главе 8. Функция у
Самостоятельная работа 36.
Функция у = х) и ее график
Вариант 1
1. 
Найдите
значение функции у = х2 , соответствующее данному значению
аргумента:
З 
6)
4
2. Найдите точки пересечения параболы у = х2 и прямой:
а) у = 9; б)у=—х.
З. Постройте график функции у = х2 на промежутке [—4; 3] и укажите на нем ее наименьшее и наибольшее значения.
Вариант 2
1. Найдите значения аргументов, которым соответствует заданное значение функции у = х .
6) 16
2. Найдите точки пересечения параболы у = х2 и прямой:
а) х = 0; б) у = 2х.
З. Постройте график функции у = х2 на промежутке [1, укажите на нем ее наименьшее и наибольшее значения.
Самостоятельная работа М 37.
Графическое решение уравнений
Вариант 1
1. Решите графически уравнение:
а) х2 = х; б) х2 = 2х—1.
2.
Решите графически уравнение: х2—6х+5 = О 
Вариант 2
1. Решите
графически уравнение: 
2 = -l-2x.
2. Решите графически уравнение: х2+4х—5=0.
М 38.
Что
означает в математике запись у =Лх)
Вариант 1
1. Дана функция у =Лх), гдеЛх) = 4—х. Запишите:
а)Л1)•, в)
х
— 4, если х < —2;
2. Дана функция у =Лх), где f(x) =
2х—2, если х 2 —2.
Вычислите: а) ЛО);
1, если —5 SxS l;
З. Постройте график функции: f(x) =Р, если l<xS2; 2х, если 2 S 4.
Вариант 2
1. Дана функция у =Лх), гдеДх) = 3+х. Запишите:
а)Л0)•,
в)
3 —х, если х < 1; 2. Дана функция у где f(x) =
х +1, если х 21.
Вычислите: а)Л 1); б)Л—2).
—2, если —4 S х 
0;
З. Постройте график функции: f(x)
— х— 2, если 0 
2;
0,5х—1, если
х 4. Решить уравнение 2х-5 3х+2 
4 З
5. Найти
значение выражения
х 2
2.
Координатная плоскость. Линейное
уравнение с двумя переменными и его график.
Линейная функция и ее график.
Линейная функция у = Кх
Взаимное расположение графиков линейныхфункций
Вариант 1
1. Изобразите на координатной прямой точки Щ 1,5) и С(4).
2. Постройте треугольник АВС, если заданы координаты его вершин: 3); В(—З; 4); С(2; —5).
З. Постройте график уравнения: = 0.
4. Найдите наибольшее значение линейной функции у = —3х+5 на промежутке [—5; 7].
5. Выясните, пересекаются ли графики функций:
у = 2х+1 иу—2х = 5?
Вариант 2
1. Изобразите на координатной прямой точки В(—2,5);
2. Постройте
треугольник АВС, если заданы координаты его вершин: АО; 1); B(-l;
З. Постройте график уравнения: 3х—5у+4 = 0.
4. Найдите наименьшее значение линейной функции у = —x—l на промежутке [—4; 5].
5. Выясните, пересекаются ли графики функций: у = 3х—3 иу+1—х = 0?
х
Вариант З
1. Изобразите на координатной прямой точки В(—0,5) и
2.
Постройте треугольник АВС, если заданы координаты его
вершин: АР; 1); Щ-2•, 1); СО, -5).
З. Постройте график уравнения: 3х—4у+2 = 0.
4. Найдите наибольшее значение линейной функции у = —5х+4 на промежутке [—2; 0].
5. Выясните, пересекаются ли графики функций:
2у=х+5 и
Вариант 4
1.
Изобразите на координатной прямой точки 
,5) и 
ср). 
2.
Постройте треугольник АВС, если заданы координаты его
вершин: А(3•, 2); вез; 2); СО; 4).
З. Постройте график уравнения: 4х—у+4 = 0.
4. Найдите наибольшее значение
линейной функции у = —2х+3 на промежутке [-2; 2]
5. Выясните, пересекаются ли графики функций: Зу = x—l иу = 4х—2?
х З
З.
Основные понятия. Метод подстановки.
Метод алгебраического сложения. Системы двух
линейных уравнений с двумя переменными
как математические модели реальных ситуаций
Вариант 1
1. Является ли решением системы уравнений
пара чисел: а) (1; 1)
2. Решите систему уравнений методом подстановки:
З. Решите методом алгебраического сложения систему урав-
нений: 
4. Решите
систему уравнений: 
3
5. Сумма цифр двузначного числа равна 9. Если это число разделить на разность его цифр, то получится 12. Найдите это число.
Вариант 2
2х
+ = 4, 
1. Является
ли решением системы уравнений 
У-2х=2 пара чисел: а)
(З; 0,5); б) (0,5; 3)?
2. Решите систему уравнений методом подстановки:
З. Решите методом алгебраического сложения систему урав2х—3 у 4, нений:
3х+ Зу =
х
4.
Решите систему уравнений: 2 З
5. Сумма цифр двузначного числа равна 15, а разность его цифр равна 1. Найдите это число.
Вариант З
1. Является
ли решением системы уравнений 
пара
чисел: а) (3; —1); 
2. Решите систему уравнений методом подстановки:
З. Решите методом алгебраического сложения систему уравх-5у=З, нений:
2х-Зу=5,
4. Решите систему уравнений: х У
5. Сумма цифр двузначного числа равна 5, а разность его цифр равна 1. Найдите это число.
Вариант 4
1. Является
ли решением системы уравнений 
пара
чисел: а) (2; 0); 
2. Решите систему уравнений методом подстановки:
З. Решите методом алгебраического сложения систему урав3х — Зу = 2, нений:
—2х +4 у = 1.
4.
Решите систему уравнений: 
5. Сумма цифр двузначного числа равна 8, а разность О. Найдите это число.
4 Т
4. 
Что
такое степень с натуральным показателем. 
Таблица основных степеней.
Свойства степени с натуральным
показателем. Умножение и деление степеней с одинаковыми показателями.
Степень с нулевым показателем
Вариант 1
1. Вычислите:
2 а) б) 40—72,
З
2. Представьте в виде степени:
15 lO З
З. Вычислите: 
39 556
4. Решите уравнение: 46 = 3289 .
х
5. Не производя вычислений, расположите в порядке возрас-
4 тания числа: (—2)2 ; (—2)3 ; (—1 —4— ; (-1 1)5.
Вариант 2
1
1. Вычислите:
3 2
а)
7
2. Представьте в виде степени:
216 183
(х? •(х3 )9 : (х4
4. 
Решите
уравнение: 
=4112 .
5. Не производя вычислений, расположите в порядке убывания числа: (2,4)4 ; (—l (—l,l (4,7)4 ; (—5)4 , 2 0 .
Вариант З
1. Вычислите:
а) 6) 2 0-3 2.
2. Представьте
в виде степени: 
а)х •х х ; б)
х 23 х 14 :х5
72 .73 З.
Вычислите:
4. Решите уравнение:3 4577 .
5. Не производя вычислений, расположите в порядке возрастания числа: (—1 3 4 ; (—2,7)4; (—2)3 ; (—5)0 ; (—7)8 .
1 Вариант 4
1. Вычислите:
• 6) 3 4-5 0 .
2. Представьте в виде степени: 16 7 8
5 7 .6' 33 .з 9
305 
= -3 1 1 1 .
5. Не производя вычислений,
асположите в порядке убывания числа: (—2)3 ; (2,4 (—3)4;
(—9) ; (—7)5 ; 
5
5.
Понятие
одночлена. Стандартный вид одночлена.
Сложение и вычитание одночленов.
Умножение одночленов. Возведение одночлена в натуральную степень.
Деление одночлена на одночлен
Вариант 1
2
3 3 4 2 
1. Приведите одночлен: 3,5а Ь а Ь с • — abc к стандарт7
ному виду.
2. Выполните действия:
б)
—ab+—ab
З. Упростите выражение: 3х у—2ху +ху—3х2у+ху2+3ху.
4. Какой одночлен необходимо поставить вместо знака , чтобы равенство было верным: *:3а 2 bc = —l7a3 b4c.
(3abc)3
) — 4
5. Упростите выражение:а з ьз с
9a2b2c2
Вариант 2
1. Приведите
одночлен: 
к стандартному виду.
2. Выполните действия:
а) 3х2-2,5х2 ; б) —ab2 +—ab 2 .
З. Упростите выражение: 2ху2+3ху-4хуЗ +2ху2—3ху+3ху .
4. Какой
одночлен необходимо поставить вместо знака , чтобы равенство было верным: 
=
6a2 b.
5. Упростите
выражение: 
(2a 2 b)3 (—ab) 2
• с2 + а7 64 
4abc2
1.
Приведите одночлен 
к стандартному виду.
2. Выполните действия:
а) 4х2-3,2х2 , б) —a 2 b+—a 2 b.
З. Упростите выражение: 3х3уЗ—ху+4ху
—3х3уЗ +2ху+2ху2
1
4.
Какой одночлен необходимо поставить вместо знака , чтобы
равенство было верным: = —7ас5
(3abc 2 • Ь 5
5.
Упростите выражение: + аз ь2 с 
—abc
Вариант 4
1 1.
Приведите одночлен: 
к стандартному
ВИДУ
2. Выполните действия:
а) 3х2 +2,6х2 б) 7abcAabc.
1 З.
Упростите выражение: 2ху —ху+3хуЗ +2ху-4ху
4.
Какой одночлен необходимо поставить вместо знака * , чтобы равенство было
верным: *:(—9a2 b) = 7ас .
5.
Упростите выражение: — a 5 bc 
16abc
х 6
М б.
Основные понятия.
Сложение и вычитание многочленов.
Умножение многочлена на одночлен.
Умножение многочлена на многочлен.
Формулы сокращенного умножения. 
Деление многочлена на одночлен
1 при 
а = 2.
7
М 7.
Что такое разложение многочленов на множители и зачем оно нужно.
Вынесение общего множителя за скобки.
Способ группировки.
Разложение многочленов на множители с помощью формул сокращенного умножения.
Разложение многочленов на множители с помощью комбинации различных приемов.
Сокращение алгебраических дробей. Тождества
Вариант 1
1. Разложите на множители:
2 З. 2—4; в) 2х+6+х2 +3х.
а) 3х+х б) I 6х
2. Решите уравнение: 2х2 +3х = 0.
5ab2 З. Сократите дробь: 
abc
4. Докажите тождество: (a+b)2—2ab+a 2—b2 = а•2а.
5. Решите уравнение: +2х2-4х—8 = 0.
Вариант 2
1. Разложите на множители:
4. 6) 28-8; в)
х2+х+2х+2.
2. Решите уравнение: 3х —х = 0. 2ab2c2 З. Сократите дробь:
b2c
4. Докажите тождество: 
—
а(За—4Ь).
5. Решите уравнение: 2х3 +х2—8х-4 = 0.
1. Разложите йа множители:
а) х2+3х4 6) 38-27; в) 2х+4+х2+2х.
2. Решите уравнение: х2—3х — о.
3abc8 З. Сократите дробь:
азьс2
4. 
Докажите
тождество:
5. Решите уравнение:
Вариант 4
1. Разложите на множители:
а) х5+х4 ; б) 28-32; в) 3х+8+3х2+8х.
2
2. Решите уравнение: 3х—4х = О. 4a2bc3 З. Сократите дробь:
2ab2
4. Докажите тождество: 
=
b2 .
5. Решите уравнение: 
= 0.
8
№ 8.
Функция у = х) и ее график.
Графическое решение уравнений. Что означает в математике запись у =Лх)
Вариант 1
1, Найдите значение функции у х- , соответствующее данному значению аргумента:
2
3
2. Постройте график функции у = х2 на промежутке [—2; 2].
З. Решите графически уравнение .х2 = 2х.
4. Дана функция у =Лх), ГДеЛХ) - х2+4х—2.
НайдитеЛ2х+ ).
х- , если —2 S х 2,
5. Постройте график функции у =
2-х, если 2 3.
Вариант 2
1. Найдите значение функции у = х2 , соответствующее данному значению аргумента:
5
2. Постройте график функции у х2 на промежутке [—3; 0].
З. Решите графически уравнение х = —2х.
4. Дана функция у =Лх), гдеЛх) = Р-5.
НайдитеЛ—3х+2).
2 — х, если —2 S х 1,
5. Постройте график функции у = х 2 , если l<xS3.
1. Найдите значение функции у = х2, соответствующее ДЕННО-
2. Постройте
график функции у = х2 на промежутке [—2; 3] 
З. Решите графически
уравнение х2 = Ах.
4. Дана функция у =Лх), гдеЛх) = —х2 +2. Найдите Л3х+ I ).
Р, если —1 5 х S 1, функции у =
5 —4х, если I <x s3 .
1. Найдите значеџие функции у = х2, соответствующее данно-
З
4
2. Постройте
график функции у = х2 на промежутке 2] 
З. Решите графически
уравнение х2 = 3х.
4. Дана функция у =Лх),
гдеЛх) = 2—х2 . НайдитеЛ2х—3
Р, если —1 5 х S 2,
5. 
Постройте
график функции у = х +2, если 2 S 4.
ОТВЕТЫ
К главе 1
Самостоятельная работа М 1
Вариант 1 Вариант 2
6) 12. з. 1,25. з. 8,5.
Самостоятельная работа № 2
|
Вариант 1 |
Вариант 2 |
|
1. а) х+у; |
1. х—у; 6)
.YZ |
|
а 2. а) а = b+c; б) — = 2ab |
2. а) а = Юс; б) a(b-c) = b+c—5. |
|
з.у+2 = 2(x-2). |
з. х+30 = 20-20). |
Самостоятельная работа № З
Вариант 1 Вариант 2
21 1. 22 1.
2
17 2. 2.
2
З. 4 км/ч. З. 60 км/ч.
Самостоятельная работа М 4
Вариант 1 Вариант 2
К главе 2
Самостоятельная работа М 5
Вариант 1 Вариант 2
Самостоятельная работа № б
Вариант 1 Вариант 2
2.
(-0,8; -1,6).
Самостоятельная работа № 7
Вариант 1 Вариант 2
Самостоятельная работа М 8
Вариант 1 Вариант 2
1. a) l •,
З. -1 из.
Самостоятельная работа № 9
Вариант 1
1. а) прямые параллельны; б) прямые пересекаются.
З. —оо и 220.
Вариант 2
1. а) прямые пересекаются; б) прямые параллельны.
К главе З
М 10
2
1. а) нет; б) да; в) нет. 1. а) да; б) нет; в) нет.
з. (1,4; 0,4).
Самостоятельная работа № 11
Вариант 1 Вариант 2
5 7
1. а)
(2,5; -0,5); 6) (-0,7; -0,8). 
6)
25 5 
2.
Самостоятельная работа № 12
Вариант 1 Вариант 2
1.
2 З
2. 54
2.
82.
К главе 4
Самостоятельная работа № 13
Вариант 1
1. а) 3,6 — основание степени, 4 — показатель степени.
б) (a+b)3 ; (а+Ь) — основание степени, З — показатель степени. l6 4
б) з.
8,75.
8175
Вариант 2
, з ; —3,1 — основание степени, 3 — показатель степени.
б) (ab)4 ; ab — основание степени, 4 — показатель степени.
27121
з. 38,5.
125
Ca.uocmoamer1bHaa pa60ma Xe 14
BapuaŒtm 1
BapuaŒtm 2
CauuocmoameJ1bHaa paõoma .Mg 15
BapuaŒtm 1 BapuaŒtm 2
|
|
6) (—ax) |
l. a) x i3 , |
6) (-2x)9 . |
|
3.0,2. |
|
2. a) x4, |
6) (a+b) 13 |
16l 
3
Ccuocmoame.rlb}tag paõoma JE 16
|
|
|
CLMocmogmeJ1bHaa paõoma JE 17
BapuaŒtm I Bapuamn 2
1. a)
24; 6) 73.
10 3.
37 
К главе 5
18
|
1. а) нет; |
б) да. |
1. а) нет; б) да. |
|
7 2. |
|
2. 0,04. |
|
З. —3a2b3c7d. |
|
20 З. —ab 3c l0d 4 . 7 |
Самостоятельная работа М 19
Вариант 1 Вариант 2
1. а) ху, 2ху и —— ху ; 1. а) ху2 2 ; ——х 2 у 2 и З,7ху ; 6
6) х2уз , 4х2уз и -0,75х29. б) х ух, —2х4у5 и 3,5х у5 .
16
2. а) 0,6х4 ; б) l—ab3 . 2. а) 5,9х3 ; б) —a 2 b 3
15 21
5445
З. 5ху+ху З. —0, lx5y3—4xy.
Самостоятельная работа М 20
Вариант 1 Вариант 2
37 4з
1. а)
35ab; б) —6ху 
1. а) -12ab; б) —28ху 
2. 64а
12 Ь 18 с .6 2. -24За Ь с 
78 4 8 12 З. —16abc. З. 9а Ь с 
Самостоятельная работа М 21
Вариант 1 Вариант 2
8 6) -3х3 . 1
4 б) —8х.
2. 9а-с 2. -17b'c5 
З. 4a
8 b 8 З. 72a8 b 5 c.
К главе 6 работа 22
Вариант
1. у4
+4у —8у2+8у.
2. 26. 2.-ll.
8З
З. 7т-зт-зт-32.
Самостоятельная работа № 23
Вариант 1 Вариант 2
1. х3 +х2—3. 1.
—4—ХЗ
7
11 2. 
6 З З. 5ху+Зх:+2у:.
 |
|
Вариант 1 |
Вариант 2 |
|
1. а) 3х2—6х; б) х у—ху2+х2у2 .
|
1. а) 8х—2х2 ; б) хЗу+х2у2—хЗуЗ . 27 2. 14 |
|
З. -17а5 +29аЗ +6а2-4Оа+Ь. |
З. 2а6—4а4+3а2 |
Самостоятельная работа № 25
|
Вариант 1 |
Вариант 2 |
|
2 1. а) х+3х-28•, |
2 1. а) -x+2x+8•, |
|
б) —2уЗ
+8у2+ |
6) -уЗ+7у2-Зу+21. |
|
2. -33. |
2. -32. |
15 З.
Самостоятельная работа № 26
|
Вариант 1 |
|
Вариант 2 |
|
1. а) х2+6х+9; |
б) 4х2—4ху+У'2. |
2 22 1. а) х+4х+4; б) 9у—6ху+х |
|
2. а) 1599; |
6) 2484. |
2. а) 896; 6) 4891 . |
|
з. 17. |
|
з. 2,5. |
55
27
|
6? 16a6-4a3b+O,25b2 . |
6? 9a' 0-15a Ь+6,25Ь2 . |
|
2. х +l25. |
2. х -216. |
42
1. а) 25х+104+у4.
Самостоятельная работа М 28
|
Вариант 1 |
Вариант 2 |
|
1. а) -х-4•, 6) 2х+3. |
— х; б)х+2. |
|
|
2. -29. |
|
З. 2a'b4c4 . |
З. 4a3 b3c5 . |
К главе 7
Самостоятельная работа № 29
Вариант 1 Вариант 2
4
1.-3;
4.
2. 6,2. 2. 10.
з. 0,25. з. 0,25.
Самостоятельная работа № 30
|
Вариант 1 |
Вариант 2 |
|
1. а) З(х+4у); б) a3 (2a2+l). |
1. а) 4(х+4у); б) a(3a+l). |
|
2. 0; 4. |
|
З. х:(2у—3х:+4уЗ
).
Самостоятельная работа М 31
Вариант 1 Вариант 2
1. 
а) (З—у)(х+З); б)
2. -16.
з. 0,01 18. з. 0,0222.
32
Вариант
б) (4т—9п)(4т+9п). б) (Зт—5п)(Зт+5п).
8
2.
З. (3х-1
Самостоятельная работа № 33
Вариант 1 Вариант 2
Самостоятельная работа М 34
Вариант 1 Вариант 2
у-з
б) 
х
2. 0,25. 2. -14.
6х З. Ьс.
Самостоятельная работа М 35
|
Вариант 1 |
Вариант 2 |
|
1. а) да; б) нег. |
1. а) нег; б) да. |
|
З. да. |
З. да. |
К главе 8
Самостоятельная работа № 36
Вариант 1 Вариант 2
9
16
з.ои 16. 
|
|
37 |
|
Вариант 1 |
Вариант 2 |
Самостоятельная работа № 38
Вариант 1 Вариант 2
2 2
б) 4+2х; в) 9х. 1.
а) З; б) 3—х; в) 4х 
2. а) -2; 6) -6,01 .
Контрольные
К главе 1
Контрольная работа № 1
Вариант 1
Вариант 2
18 23 1.
з. 28 4.
7 6
Вариант З
5
1. 5,6 3. 24
Вариант 4
45 24
1. 
з. 18 4. 
7 7
К главе 2
Контрольная работа М 2
Вариант 1
Вариант 2 Вариант З Вариант 4 
4. 20.
5. нет. 5. да. 5. нет. 5. да.
К главе З
Контрольная работа № З
Вариант
|
1. а) нет; б) да. Вариант 2 |
|
з. (-23; -7). 4. (-15; 20). 5. 36. |
|
|
5 1 |
2 з. 4. (1,6; 2,4). 5.78 или 87. |
|
1. а) нет; б) да. 2. |
||
59
|
Вариант З |
Вариант 4 |
|
|
1. а) да; б) нет. |
1. а) да; |
б) нет. |
|
Вариант 2 |
|
|
|
9 1. а) 6) 31. 49
Вариант З |
З. 1 17
|
4. 41 12. |
|
9 |
5 |
4. 4577. |
|
25 |
|
6 |
|
|
Вариант 4 |
|
|
|
|
6) 80. |
|
з. 981. |
4. -31 1 1 |
 |
2. (3,8; 0,2). 
|
5. 32 или 23, 5. 44. К главе 4 Контрольная работа № 4 Вариант 1 |
|
|
з. -52. 27 |
4. 3289. |
49
3 ; (-7)5 .
60
К главе 5
Контрольная работа М 5
|
Вариант 1 |
Вариант 2 |
||
|
1. —a6b8c4. |
2 1. —l,labSc3 . |
||
|
17 |
2.
а) 0,5х2; 6) —аь2 |
||
|
21 |
15 |
||
|
|
|
З. 4ху2—ху |
|
|
4.—5 la b5c6 . |
|
4. —24a3 b6c, |
|
|
5. 2аЗ ЬЪс4 . |
|
5. 3а7Ь4 . |
|
|
Вариант З |
|
Вариант 4 |
|
|
1. —4,5a3b2c8 . |
|
1. —30a3b6c2. |
|
|
2. а) 0,8х2; |
б) —a 2 b 20 |
2. а) 5,6х2; |
б) ЗаЬс. |
|
З. ху+6ху2. |
|
3 З. ху+?. |
|
|
4. —42a4bc9. |
|
4. —63а bc4 |
|
|
5. —35a3b2c 5 . |
|
5. 15a5 bc 7. |
|
К главе 6
Контрольная работа № б
Вариант 1
1.x3+l.
2. а) 2х2+2х; б) хзу—х2у2
З. а) х2—4х+4; б) 9х4+6х2у2+у
23
63
Вариант З
1. x3 +2x—l .
2. а) 2х2-8х•, б) хЗу+х2у3.
З. а) 9х2
+6х+1 ; б) х2—2хуЗ+у6
21 5.
20
Вариант 2
1. 4х—х 
2. а) 3х2—6х; б) хЗу2+2х2уЗ .
З. а) 4х2+16х+16;
1 17 5. 
29
Вариант 4
1. 4х—х2—2.
2. а) 6х2—3х; б) х2у3
+ху4
З. а) 4х2—16х+16; б) 4х2+4хуЗ+у6
5.
2
61
|
К главе 7 Контрольная работа № 7 Вариант 1 2 |
1. а) х(х+3); 
56 2. З.
|
2 Вариант 2 3 1. а) х(х+ |
с
|
З. 2ас.
Вариант З
22 +l ); З)(а+З);
1. а) x(3x
6
з. 2 
а
|
Вариант 4 4 1. а) х(х+ I ); |
|
|
4 |
2асз |
З. 
в) (х+2)(х+З).
в) (х+ I )(х+2).
5.-2; ; 2.
2
в) (х+2)2 .
в) (x+l )(Зх+8).
К главе 8 Контрольная работа М 8
|
Вариант 1 4 |
Вариант 2 |
|
|
9 |
|
25 |
|
4. 4f+12х+3. |
2 4. 9х-12х-1 . |
|
|
Вариант З |
Вариант 4 |
9 |
|
4 |
|
16 |
|
3. 0 —4 |
3.0 з |
|
|
4. —6х—9х2. |
4. |
|
62
Справочное издание
Попов Максим Александрович
Контрольные и самостоятельные работы по алгебре
К учебнику А.Г. Мордковича «Алгебра. 7 класс»
7 класс
Издательство «ЭКЗАМЕН»
Гигиенический сертификат
№ }7.99.60.953.д.007297.05.10 от 07.05.201 г.
Главный редактор Л.Д. Лаппо
Редактор И.М. Бокова
Корректор ИД. Баринская
Дизайн обложки АЮ Горелик
Компьютерная верстка Н. А. Кирьянова, ЕЮ. Лысова
105066, Москва, ул. Нижняя Красносельская, д. 35, стр. 1. www.examen.biz
E-mail: по общим вопросам: info@examen.biz; по вопросам реализации: sale@examen.biz тел./факс 641-00-30 (многоканальный)
Общероссийский классификатор прощкции
ОК 005-93, том 2; 953005 — книги, брошюры, литература учебная
Текст отпечатан с диапозитивов в ОАО «Владимирская книжная типография»
600000, г.
Владимир, Октябрьский проспект, д. 7 
Качество печати соответствует качеству
предоставленных диапозитивов 
По вопросам реализации обращаться по тел.: 641-00-30 (многоканальный).
[1] . Решите систему уравнений методом подстановки:
Х+4у=5.
З. Решите систему уравнений:
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
7
4
