Министерство науки и высшего образования Российской Федерации

 

 

Факультет экономики и права

 

Кафедра педагогического образования

 

 

 

 

 

 

 

 

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Естествознание»

вариант 12

 

 

 

 

 

 

 

 

	Руководитель работы   _____________  «_____»________________2021г.
	Исполнитель студент группы  _____________  «_____»________________2021 г. Нормоконтролер______________ «____»_________________2021г.

 

 

 

 

 

 

 

 2021

 

Содержание

 

 

 

Введение …………………………………………………..……………..……3

1.     Общая и специальная теории относительности………………………..4

2. Хаос и Гармония…………………………………………………………13

Заключение …………………………….………………...…………………..16

Список использованных источников ……….………………..……….……17

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Название “теория относительности” возникло из наименования основного принципа (постулата), положенного Пуанкаре и Эйнштейном в основу из всех теоретических построений новой теории пространства и времени.

Содержанием теории относительности является физическая теория пространства и времени, учитывающая существующую между ними взаимосвязь геометрического характера.

Общая теория относительности (ОТО) - современная теория тяготения, связывающая его с кривизной четырехмерного пространства-времени.

Специальная теория относительности (СТО) - фундаментальная физическая теория пространственно-временных свойств всех физических процессов.

Целью является рассмотрение основных представлений о специальной и общей теории относительности, существующих в современной физике.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1Общая и специальная теории относительности

 

 

1.1 Принцип эквивалентности и геометризация тяготения

 

Факт этот по существу был установлен еще Галилеем. Он хорошо известен каждому успевающему старшекласснику: все тела движутся в поле тяжести (в отсутствие сопротивления среды) с одним и тем же ускорением, траектории всех тел с заданной скоростью искривлены в гравитационном поле одинаково. Благодаря этому, в свободно падающем лифте никакой эксперимент не может обнаружить гравитационное поле. Иными словами, в системе отсчёта, свободно движущейся в гравитационном поле, в малой области пространства-времени гравитации нет. Последнее утверждение – это одна из формулировок принципа эквивалентности.

 

Данное свойство поля тяготения отнюдь не тривиально. Достаточно вспомнить, что в случае электромагнитного поля ситуация совершенно иная. Существуют, например, подзаряженные, нейтральные тела, которые электромагнитного поля вообще не чувствуют. Так вот, гравитационно-нейтральных тел нет, не существует ни линеек, ни часов, которые не чувствовали бы гравитационного поля. Эталоны привычного евклидова пространства меняются в поле тяготения.

Геометрия нашего пространства оказывается неевклидовой.

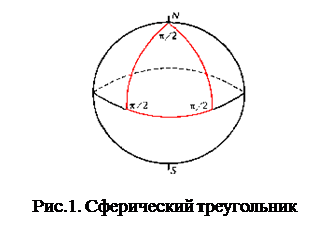
Некоторое представление о свойствах такого пространства можно получить на простейшем примере сферы, поверхности обычного глобуса. Рассмотрим на ней сферический треугольник – фигуру, ограниченную дугами большого радиуса. (Дуга большого радиуса, соединяющая две точки на сфере, – это кратчайшее расстояние между ними: она естественный аналог прямой на плоскости.) Выберем в качестве этих дуг участки меридианов, отличающихся на 90^o долготы, и экватора (рис. 1). Сумма углов этого сферического треугольника отнюдь не равна сумме углов π,треугольника на плоскости:

 

 

Заметим, что превышение суммы углов данного треугольника может быть выражено через его площадь S и радиус сферы R:

 

 

Можно доказать, что это соотношение справедливо для любого сферического треугольника. Заметим также, что обычный случай треугольника на плоскости тоже вытекает из этого равенства: плоскость может рассматриваться как сфера с R→∞

 

 

Перепишем формулу (2) иначе:

 

 

Отсюда видно, что радиус сферы можно определить, оставаясь на ней, не обращаясь к трехмерному пространству, в которое она погружена. Для этого достаточно измерить площадь сферического треугольника и сумму его углов. Иными словами, K (или R) является внутренней характеристикой сферы. Величину K принято называть гауссовой кривизной, она естественным образом обобщается на произвольную гладкую поверхность:

Здесь углы и площадь относятся к малому треугольнику на поверхности, ограниченному линиями кратчайших расстояний на ней, а кривизна, вообще говоря, меняется от точки к точке, является величиной локальной. И в общем случае, так же как и для сферы, K служит внутренней характеристикой поверхности, не зависящей от ее погружения в трехмерное пространство. Гауссова кривизна не меняется при изгибании поверхности без ее разрыва и растяжения. Так, например, конус или цилиндр можно разогнуть в плоскость, и поэтому для них, так же как для плоскости, K = 0.

 

 

На соотношения (3), (4) полезно взглянуть несколько иначе. Вернемся к рисунку 1. Возьмем на полюсе вектор, направленный вдоль одного из меридианов, и перенесем его вдоль этого меридиана, не меняя угла между ними (в данном случае нулевого), на экватор. Далее, перенесем его вдоль экватора, снова не меняя угла между ними (на сей раз  π/2), на второй меридиан. И наконец, таким же образом вернемся вдоль второго меридиана на полюс. Легко видеть, что, в отличие от такого же переноса по замкнутому контуру на плоскости, вектор окажется в конечном счете повернутым относительно своего исходного направления на π/2, или на

Этот результат, поворот вектора при его переносе вдоль замкнутого контура на угол, пропорциональный охваченной площади, естественным образом обобщается не только на произвольную двумерную поверхность, но и на многомерные неевклидовы пространства. Однако в общем случае n-мерного пространства кривизна не сводится к одной скалярной величине K(x). Это более сложный геометрический объект, имеющий n²(n² - 1)/12 компонентов. Его называют тензором кривизны, или тензором Римана, а сами эти пространства – римановыми. В четырехмерном римановом пространстве-времени общей теории относительности тензор кривизны имеет 20 компонентов.

 

1.2 Классические опыты по проверке ОТО

 

В начале предыдущего раздела уже отмечалось, что гравитационное поле влияет на движение не только массивных тел, но и света. В частности, фотон, распространяясь в поле Земли вверх, совершает работу против силы тяжести и поэтому теряет энергию. Как известно, энергия фотона пропорциональна его частоте, которая, естественно, тоже падает. Этот эффект – красное смещение – был предсказан Эйнштейном еще в 1907 году. Нетрудно оценить его величину. Работа против силы тяжести, очевидно, пропорциональна gh, где g – ускорение свободного падения, а h – высота подъема. Произведение gh имеет размерность квадрата скорости. Поэтому результат для относительного смещения частоты выглядит из соображений размерности так:

 

 

где c = 3 ^. 10¹⁰ см/с – скорость света. При  g≈10³ см/с², h~10³ см относительное смещение ничтожно мало ~10^-15. Неудивительно, что экспериментально красное смещение удалось наблюдать лишь спустя полвека, с появлением техники, использующей эффект Мёссбауэра. Это сделали Паунд и Ребка.

 

 

Еще один эффект, предсказанный Эйнштейном на заре ОТО, – отклонение луча света в поле Солнца. Его величину нетрудно оценить следующим образом. Если характерное, прицельное, расстояние луча от Солнца равно ρ, то радиальное ускорение составляет  GM/ρ², где G – ньютоновская гравитационная постоянная, а M – масса Солнца. За характерное время пролета  ρ/c радиальная компонента скорости фотона изменится на GM/(ρc) и угол отклонения составит соответственно

Удобно ввести часто используемую в ОТО характеристику массивного тела, так называемый гравитационный радиус:

 

 

Наивное использование полуклассических соображений действительно приводит к ответу

Именно этот результат был получен Эйнштейном в одном из первоначальных вариантов ОТО. Первая мировая война воспрепятствовала проверке, неблагоприятной для теории. Окончательный, правильный результат ОТО вдвое больше:

 

 

Гравитационный радиус Солнца r_g≈3 км, а прицельный параметр естественно сделать как можно ближе к обычному радиусу Солнца, который составляет 7 ^. 10⁵ км. Таким образом, для луча света, проходящего вблизи поверхности Солнца, угол отклонения равен 1,75". Измерения, проведенные группой Эддингтона во время солнечного затмения 1919 года, подтвердили последнее предсказание. Это был подлинный триумф молодой общей теории относительности.

И наконец, к числу классических тестов ОТО относится также вращение перигелия орбиты Меркурия. Замкнутые эллиптические орбиты – это специфика нерелятивистского движения в притягивающем потенциале 1/r. Неудивительно, что в ОТО орбиты планет незамкнуты. Малый эффект такого рода удобно описывать как вращение перигелия эллиптической орбиты. Задолго до появления ОТО астрономы знали, что перигелий орбиты Меркурия поворачивается за столетие примерно на 6000" . Поворот этот в основном объяснялся гравитационными возмущениями движения Меркурия со стороны других планет Солнечной системы. Оставался, однако, неустранимый остаток – около 40" в столетие. В 1915 году Эйнштейн объяснил это расхождение в рамках ОТО.

Из простых соображений размерности можно ожидать, что поворот перигелия за один оборот составляет

 

 

где R – радиус орбиты. Аккуратный расчет в рамках ОТО для орбиты, близкой к круговой, дает

 

 

При радиусе орбиты Меркурия R≈0.6^.10⁸ км это дает 43" в столетие, снимая таким образом существовавшее расхождение. Ясно, кстати, чем выделяется в этом отношении Меркурий: это планета, ближайшая к Солнцу, планета с наименьшим радиусом орбиты R. Поэтому вращение перигелия орбиты у нее максимально.

 

 

1.3 Черные дыры

 

Однако роль ОТО отнюдь не сводится к исследованию малых поправок к обычной ньютоновской гравитации. Существуют объекты, в которых эффекты ОТО играют ключевую роль, важны стопроцентно. Это так называемые черные дыры.

Еще в XVIII веке Митчел и Лаплас независимо заметили, что могут существовать звезды, обладающие совершенно необычным свойством: свет не может покинуть их поверхность. Рассуждение выглядело примерно так. Тело, обладающее радиальной скоростью v, может покинуть поверхность звезды радиусом R и массой M при условии, что кинетическая энергия этого тела mv2/2 превышает энергию притяжения GMm/R,т.е. при v2 > 2GM/R. Последовательное применение ОТО приводит к такому же выводу, причем, поразительно, правильный критерий количественно совпадает с наивным, необоснованным. Величина rg, гравитационный радиус, уже встречалась раньше (см. формулу (7)).

Черная дыра – вполне естественное название для такого объекта. Свойства его весьма необычны. Черная дыра возникает, когда звезда сжимается настолько сильно, что усиливающееся гравитационное поле не выпускает во внешнее пространство ничего, даже свет. Поэтому из черной дыры не выходит никакая информация.

Занятно выглядит падение пробного тела на черную дыру. По часам бесконечно удаленного наблюдателя это тело достигает гравитационного радиуса лишь за бесконечное время. С другой стороны, по часам, установленным на самом пробном теле, время этого путешествия вполне конечно.

Многочисленные результаты астрономических наблюдений дают серьезные основания полагать, что черные дыры – это не просто игра ума физиков-теоретиков, а реальные объекты, существующие по крайней мере в ядрах галактик.

 

 

 

1.4 Эйнштейновский принцип относительности

 

Специальная теория относительности (СТО) наряду с предположением о том, что

a) пространство - трёхмерно, однородно и изотропно, (что означает, что в пространстве нет выделенных мест и направлений)

б) время - одномерно и однородно, (нет выделенных моментов времени) использует следующие два основополагающие принципа:

1. Никакими физическими опытами внутри замкнутой физической системы нельзя определить, покоится ли эта система или движется равномерно и прямолинейно (относительно системы бесконечно удаленных тел). Этот принцип называют принципом относительности Галилея - Эйнштейна, а соответствующие системы отсчёта - инерциальными.

2. Существует предельная скорость (мировая константа c) распространения физических объектов и воздействий, которая одинакова во всех инерциальных системах отсчета. Со скоростью c распространяется свет в вакууме.

Прямая проверка независимости скорости света от скорости источника была выполнена А.М. Бонч-Бруевичем в 1956 г. с использованием света, испускаемого экваториальными краями солнечного диска. Скорости диаметрально противоположных участков диска (за счет вращения Солнца) отличаются на 3,5•103м/с, а скорость испущенного ими света изменялась на 65-240м/c. В пределах точности эксперимента, которая составляла [(v)/( v)] 7•10-2, зависимость скорости света от скорости источника не наблюдалось.

Таким образом, все физические явления, включая распространение света (и, следовательно, все законы природы), в различных инерциальных системах отсчета выглядят совершенно одинаково. Такая особенность Законов Природы носит название лоренцевой инвариантности (от латинского invariantis - неизменяющийся).

Согласно СТО, если скорость частицы меньше скорости света в вакууме c в некоторой инерциальной системе отсчета в данный момент времени, то она не может быть сделана равной или большей c ни кинематически - переходом в другую систему отсчета, ни динамически - изменением скорости частицы, приложенными к ней силами. Поэтому распространение электромагнитных волн в вакууме является самым быстрым способом распространения взаимодействия в физических системах.

Это положение принято распространять на все типы частиц и взаимодействий, хотя прямая проверка осуществлена только для электромагнитного взаимодействия.

Существование предельной скорости распространения взаимодействия приводит к ограничениям на модели в релятивистской физике. Оказывается, например, недопустимой модель абсолютно твердого тела, так как под воздействием приложенной к нему силы, все точки тела мгновенно изменяют свои механические состояния.

В упомянутой статье Эйнштейн проанализировал свойства времени и кажущееся "очевидным" понятие одновременности. Он показал, что классическая механика приписывает времени такие свойства, которые, вообще говоря, не согласуются с опытом и являются правильными только при малых скоростях движения. Одним из центральных пунктов эйнштейновского анализа понятия времени является синхронизация часов, т.е. установление единого времени в пределах одной инерциальной системы отсчета. Если двое часов находятся в одной точке пространства (т.е. в непосредственной близости), то их синхронизация производится непосредственно - стрелки ставятся в одно и то же положение (полагают, что часы совершенно одинаковы и абсолютно точны).

Синхронизацию часов, находящихся в двух разных точках пространства, Эйнштейн предложил проводить с помощью световых сигналов. Испустим из точки A в момент t₁ короткий световой сигнал, который отразится от некоторого зеркала B и вернется в точку A в момент t₂. Времена распространения сигнала туда и обратно конечны (скорость сигнала конечна!) и одинаковы (изотропия пространства!). Поэтому часы в точке B будут согласованы с показаниями часов в точке A в моменты испускания (t₁) и возвращения (t₂) сигнала соотношениями

 

t₁ = t_B - h/c, t₂ = t_B + h/c,

 

где h = r_AB - расстояние между точками A и B. Отсюда положение, в которое нужно поставить стрелки часов B в момент прихода сигнала: t_b = (t₁ + t₂)/2. Таким способом можно синхронизовать показания всех часов, неподвижных друг относительно друга в некоторой инерциальной системе отсчета S.

Мысленные эксперименты с движущимися часами, аналогичные только что описанному, показывают, что здесь синхронизация невозможна и единого для всех инерциальных систем времени не существует.

Пусть наблюдатель A находится посередине длинного поезда, движущегося со скоростью сравнимой со скоростью света, а наблюдатель B стоит на земле вблизи железнодорожного полотна. Устройства, находящиеся в хвосте и в голове поезда на одинаковых расстояниях от A, испускают две короткие вспышки света, которые достигают наблюдателей A и B одновременно - в тот момент, когда они поравняются друг с другом. Какие выводы сделают из одновременного прихода к ним световых сигналов наблюдатели в поезде и на земле?

Наблюдатель A: Сигналы испущены из точек, удаленных от меня на равные расстояния, следовательно, они и испущены были одновременно.

Наблюдатель B: Сигналы пришли ко мне одновременно, но в момент испускания голова поезда была ко мне ближе, поэтому сигнал от хвоста поезда прошел больший путь, следовательно он и был испущен раньше, чем сигнал от головы.

Этот пример показывает, что часы в системе "поезд" синхронизованы только с точки зрения наблюдателя, который в ней неподвижен. С точки зрения наблюдателя на земле, часы, расположенные на поезде в разных точках (в голове, в хвосте и в середине поезда) показывают разное время. События, одновременные в одной системе отсчета (световые вспышки в системе отсчета поезда), не являются одновременными в другой системе отсчета земли. Синхронизация часов находящихся в разных системах отсчета невозможна. Этот вывод не исключает совпадения показаний часов в отдельный момент времени - например, наблюдатели A и B в момент встречи могут установить одинаковые показания своих часов. Но уже в любой последующий момент показания часов разойдутся.

Преобразования Лоренца, обобщающие формулы Галилея перехода от одной инерциальной системы отсчета в другую, можно получить из анализа еще одного мысленного эксперимента. Пусть начала координат систем отсчета S и S^ в начальный момент t = t^ совпадают и оси координат в них имеют одинаковую ориентацию (Рис. 6). В этот момент времени в их общем начале координат пусть произошла световая вспышка. С точки зрения наблюдателя, находящегося в системе S, в ней распространяется сферическая электромагнитная волна, которая за время t пройдет расстояние r = c t   (  ) от начала координат.

Но наблюдатель в движущейся системе S^ также регистрирует сферическую световую волну, распространяющуюся из начала координат этой системы (точки 0^) со скоростью света в вакууме c. По его часам за время t^ волна пройдет расстояние r^ = c t^, где . Это связано с тем, что физические явления в инерциальных системах происходят одинаковым образом. Иначе, регистрируя различия, можно было бы найти "истинно" покоящуюся систему отсчета, что невозможно.

Теперь ясно, что координаты точек волнового фронта в системе S и S^ связаны уравнением

 

решение которого и является искомым обобщением преобразований перехода из одной инерциальной системы координат в другую.

Опуская сам формальный вывод, который использует общие соображения об однородности и изотропии пространства и однородности времени (из которых, например, следует, что связь "штрихованных" и "нештрихованных" координат должна быть линейной), можно получить, что в условиях рассматриваемого мысленного эксперимента, параметры {x^,y^,z^,t^} связаны с параметрами {x,y,z,t}.

Преобразования Лоренца оставляют неизменными уравнения Максвелла, однако проверка этого утверждения выходит за рамки школьной программы по физике.

Легко видеть, что уравнения Ньютона теперь не сохраняют свой вид при преобразовании (12). Поэтому второй закон Ньютона необходимо модифицировать. Новая механика, основанная на принципе относительности Эйнштейна, называется релятивистской (от латинского relativus - относительный).

При безразмерном параметре V/c 1 формулы (4) переходят в формулы (1). Поэтому в теории относительности выполняется принцип соответствия - при малых скоростях движения частиц и систем отсчета релятивистские выражения переходят в формулы ньютоновой механики. Этот переход является характерной чертой любой физической теории: старые знания не перечеркиваются новыми достижениями, а включаются них как предельный частный случай.

Обратное преобразование координат системы S в координаты системы S^ можно получить из (12), поменяв местами штрихованные и нештрихованные координаты и проведя замену V  - V:

Если частица движется относительно движущейся системы координат S^ со скоростью , то ее скорость в системе отсчета S может быть найдена с помощью преобразований Лоренца (12).

Если закон движения частицы в движущейся системе координат имеет вид

 

 

то в покоящейся (лабораторной) системе координат этот закон, очевидно, имеет вид

 

 

Выполнив подстановку (13), найдем, что

 

Эта формула определяет релятивистский закон сложения скоростей.

При  = V/c  0 релятивистский закон сложения скоростей (13) с точностью до линейных по  членов переходит в формулу преобразования скоростей в классической механике:

 

 

Из (13) следует, что скорость частицы меньшая скорости света в вакууме (v^ c) в одной системе отсчета, останется меньше скорости света в вакууме (v c) в любой другой системе отсчета, движущейся по отношению к первой с досветовой скоростью V c. Если же ^ = (c,0,0), то = (c,0,0): скорость света одна и та же во всех системах отсчета.

 

 

2Хаос и Гармония.

 

Хаос, понятие окончательно оформившееся в древнегреческой философии – это трагический образ космического первоединства, начало и конец всего, вечная смерть всего живого и одновременно принцип и источник всякого развития, он неупорядочен, всемогущ и безлик.

Идеи Брюссельской школы, существенно опирающиеся на работы Пригожина, образуют новую, всеобъемлющую теорию изменений.

В сильно упрощенном виде суть этой теории сводится к следующему. Некоторые части Вселенной действительно могут действовать как механизмы. Таковы замкнутые системы, но они в лучшем случае составляют лишь малую долю физической Вселенной. Большинство же систем, представляющих для нас интерес, открыты — они обмениваются энергией или веществом (можно было бы добавить: и информацией) с окружающей средой. К числу открытых систем, без сомнения, принадлежат биологические и социальные системы, а это означает, что любая попытка понять их в рамках механической модели заведомо обречена на провал.

Кроме того, открытый характер подавляющего большинства систем во Вселенной наводит на мысль о том, что реальность отнюдь не является ареной, на которой господствует порядок, стабильность и равновесие: главенствующую роль в окружающем нас мире играют неустойчивость и неравновесность.

Если воспользоваться терминологией Пригожина, то можно сказать, что все системы содержат подсистемы, которые непрестанно флуктуируют. Иногда отдельная флуктуация или комбинация флуктуацией может стать (в результате положительной обратной связи) настолько сильной, что существовавшая прежде организация не выдержит и разрушится. В этот переломный момент (который авторы книги называют особой точкой или точкой бифуркаци) принципиально невозможно предсказать, в каком направлении будет происходить дальнейшее развитие: станет ли состояние системы хаотическим или она перейдет на новый, более дифференцированный и более высокий уровень упорядоченности или организации, который авторы называют диссипативной структурой. (Физические или химические структуры такого рода получили название диссипативных потому, что для их поддержания требуется больше энергии, чем для поддержания более простых структур, на смену которым они приходят).

Один из ключевых моментов в острых дисскусиях, развернувшихся вокруг понятия диссипативной структуры, связан с тем, что Пригожин подчеркивает возможность спонтанного возникновения порядка и организации из беспорядка и хаоса в результате процесса самоорганизации.

Обобщая, мы можем утверждать, что в состояниях, далеких от равновесия, очень слабые возмущения, или флуктуации, могут усиливаться до гигантских волн, разрушающих сложившуюся структуру, а это проливает свет на всевозможные процессы качественного или резкого (не постепенного, не эволюционного) изменения. Факты, обнаруженные и понятые в результате изучения сильно неравновесных состояний и нелинейных процессов, в сочетании с достаточно сложными системами, наделенными обратными связями, привели к созданию совершенно нового подхода, позволяющего установить связь фундаментальных наук с «переферийными» науками о жизни и, возможно, даже понять некоторые социальные процессы.

Знаменитое второе начало (закон) термодинамики в формулировке немецкого физика Р. Клаузиуса звучит так: «Теплота не переходит самопроизвольно от холодного тела к более горячему».

Закон сохранения и превращения энергии (первое начало термодинамики), в принципе, не запрещает такого перехода, лишь бы количество энергии сохранялось в прежнем объеме. Но в реальности это никогда не происходит. Данную односторонность, однонаправленность перераспределения энергии в замкнутых системах и подчеркивает второе начало термодинамики.

Для отражения этого процесса в термодинамику было введено новое понятие — «энтропия». Под энтропией стали понимать меру беспорядка системы. Более точная формулировка второго начала термодинамики приняла такой вид: при самопроизвольных процессах в системах, имеющих постоянную энергию, энтропия всегда возрастает.

Физический смысл возрастания энтропии сводится к тому, что состоящая из некоторого множества частиц изолированная (с постоянной энергией) система стремится перейти в состояние с наименьшей упорядоченностью движения частиц. Это и есть наиболее простое состояние системы, или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу.

Однако, исходя из теории изменений Пригожина, энтропия — не просто безостановочное соскальзывание системы к состоянию, лишенному какой бы то ни было организации. При определенных условиях энтропия становится прародительницей порядка.

Динамический хаос — явление в теории динамических систем, при котором поведение нелинейной системы выглядит случайным, несмотря на то, что оно определяется детерминистическими законами. Причиной появления хаоса является неустойчивость по отношению к начальным условиям и параметрам: малое изменение начального условия со временем приводит к сколь угодно большим изменениям динамики системы.

Так как начальное состояние физической системы не может быть задано абсолютно точно (например, из-за ограничений измерительных инструментов), то всегда необходимо рассматривать некоторую (пусть и очень маленькую) область начальных условий. При движении в ограниченной области пространства экспоненциальная расходимость с течением времени близких орбит приводит к перемешиванию начальных точек по всей области. После такого перемешивания бессмысленно говорить о координате частицы, но можно найти вероятность ее нахождения в некоторой точке.

Примерами хаотических динамических систем могут являться подкова Смейла и преобразование пекаря.

Обратным, в некотором смысле, к динамическому хаосу является динамическое равновесие.

Созидающий Аспект Хаоса, вытекает из необходимости эволюции  Иерархий  Божественных Сущностей, что метафизически именно через Хаос являются Сынами Парабрамана. Из пахтанья его Вод появляются Новые Вселенные, для которых он готовит Формы и Законы. Это единственный Аспект Хаоса, в котором он выступает латентным питающим Принципом и скорее Судьёй Парабрамана …его десницей. Потому как дальше и ближе к формам Парабраман отстраняется от соприкосновения с духом. Давая возможность вселенным развиваться по их путям…

Энтропия – властительница Вселенной. Во всем неживом мире в ходе всякого природного процесса нарастает хаос. Жизнь как бы существует в обратном времени. Когда-то Гегель, иллюстрируя мысль о случайности, спрашивал: сколько раз нужно рассыпать наборный шрифт, чтобы из букв сложилась строфа «Илиады»? По случайности хаос может родить гармонию, но не в масштабах высокой поэзии. Впрочем, са­ма жизнь есть грандиозная высокая гармония, случайно и необходимо рожденная хаосом. Древние атомисты представляли себе этот процесс так: изначально потоки атомов летели во вселенной параллельно друг другу. Один из атомов самопроизвольно отклонился от параллельного движения, столкнулся с двигавшимся рядом и заставил его тоже откло­ниться и столкнуться с соседним атомом - так начался хаос, из которого и родилась гармония - мир звезд, планет и вещей. Если бы мы проделали предложенный Гегелем опыт, несколько изме­нив условия, мы бы получили модели обоих процессов: бытия неоргани­ческой природы (энтропии) и развития жизни (рождения гармонии из ха­оса). Жизнь как антитеза всей природе, противотечение вселенной.

 

 

 

 

 

 

 

 

Заключение

 

ОТО – завершенная физическая теория. Она завершена в том же смысле, что и классическая механика, классическая электродинамика, квантовая механика. Подобно им, она дает однозначные ответы на физически осмысленные вопросы, дает четкие предсказания для реально осуществимых наблюдений и экспериментов. Однако, как и всякая иная физическая теория, ОТО имеет свою область применимости. Так, вне этой области лежат сверхсильные гравитационные поля, где важны квантовые эффекты. Законченной квантовой теории гравитации не существует.

ОТО – удивительная физическая теория. Она удивительна тем, что в ее основе лежит, по существу, всего один экспериментальный факт, к тому же известный задолго до создания ОТО (все тела падают в поле тяжести с одним и тем же ускорением). Удивительна тем, что она создана в большой степени одним человеком. Но прежде всего ОТО удивительна своей необычайной внутренней стройностью, красотой. Не случайно Ландау говорил, что истинного физика-теоретика можно распознать по тому, испытал ли человек восхищение при первом же знакомстве с ОТО.

Примерно до середины 60-х годов ОТО находилась в значительной мере вне основной линии развития физики. Да и развитие самой ОТО отнюдь не было весьма активным, оно сводилось в большой степени к выяснению определенных тонких мест, деталей теории, к решению пусть важных, но достаточно частных задач.

Вероятно, одна из причин такой ситуации состоит в том, что ОТО возникла в некотором смысле слишком рано, Эйнштейн обогнал время. С другой стороны, уже в его работе 1915 года теория была сформулирована в достаточно завершенном виде. Не менее важно и то обстоятельство, что наблюдательная база ОТО оставалась очень узкой. Соответствующие эксперименты чрезвычайно трудны. Достаточно напомнить, что красное смещение удалось измерить лишь спустя почти 40 лет после того, как было обнаружено отклонение света в поле Солнца.

СТО возникла больше для решения специальных задач и  никоим образом не противоречит принципам ОТО. Она лишь дополнение реального состояния науки с точки зрения потребности современной физики и естествознания. Релятивизм не мертв, он лишь отражение состояния научно-технической мысли того времени.

Тем не менее, в настоящее время СТО – бурно развивающаяся область современной физики. Это результат огромного прогресса наблюдательной астрономии, развития экспериментальной техники, впечатляющего продвижения в теории.

 

 

 

Список использованных источников

 

 

1. Михайлова, Л.А. Концепции современного естествознания: учебник для вузов. /Л.А.Михайлова – СПб.: Питер, 2009.-335с.- ISBN 978-5-91180-778-8

2. Горелов, А.А. Концепции современного естествознания: учебное пособие. / А.А.Горелов – М.: Издательство Юрайт, 2010.-335с.- ISBN 978-5-9916-0482-6

3                   Грушевицкая, Т.Г. Концепции современного естествознания: учебное пособие./ Т.Г.Грушевицкая, А.П.Садохин – М.: Высшая школа, 2007. – 383 с. - ISBN 5-7410-0106-8.

4                   Данилова, В.С. Основные концепции современного естествознания: учебн. пособие для вузов./ В.С.Данилова, Н.Н.Кожевников - М.: Аспект Пресс, 2007. –256 с.- ISBN 5-7695-3606-3.

5                   Дубнищева, Т.Я. Современное естествознание./ Т.Я.Дубнищева - М.: «Маркетинг», 2007. – 160 с. - ISBN 978-5-85939-681-8

6                    Рузавин, Г.И. Концепции современного естествознания: учебник. / Г.И.Рузавин – М.: Проспект, 2010.- 288с. – ISBN 978-5-392-01074-5

7                   Карпенков, С.Х Концепции современного естествознания: практикум. / С.Х.Карпенков – М.: Высшая школа, 2007.- 327с.- ISBN 978-5-06-004257-3

8                   Найдыш, В. М. Концепции современного естествознания: учебник для вузов / В. М. Найдыш - Москва: Альфа-М, 2008. - 704 с. - ISBN 978-5-98281-102-8.

 

 

 

 

 

 

Скачано с www.znanio.ru