
Министерство науки и высшего образования Российской Федерации
Факультет экономики и права
Кафедра педагогического образования
КОНТРОЛЬНАЯ РАБОТА
по дисциплине "Математика"
|
|
|
Руководитель работы: |
|
|
|
_____________ |
|
|
|
«_____» ____________2019г. |
|
|
|
Выполнил студент группы: |
|
|
|
_____________ |
|
|
|
«______» ___________2019г. |
2019 год
Задание 1.Дана матрица А и многочлен F(х)= х -1 + 3х2 - 5х + 7. Вычислите F(А):
|
2в. A=
|
|
|
Вычислим ![]()
1)
![]()
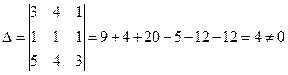
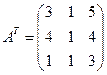
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
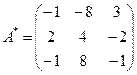

2)
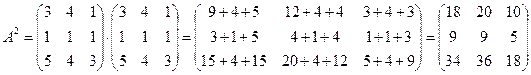
3)
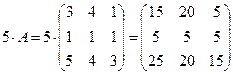
4)
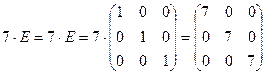
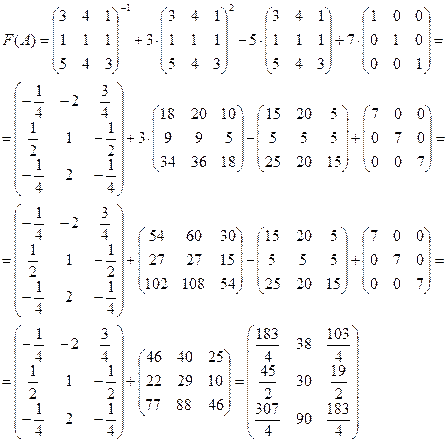
Задание 2. Вычислить
алгебраическое дополнение ![]() ; определитель
; определитель ![]() , разложив его по элементам
, разложив его по элементам ![]() - строки; разложив его по элементам
- строки; разложив его по элементам
![]() - столбца, предварительно получить
нули.
- столбца, предварительно получить
нули.
|
2.в
|
|
|
Решение:
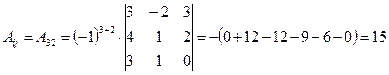
1) Вычислим определитель, предварительно получив нули третьей строке
Умножим элементы первого столбеца на (-2) и сложим с элементами второго столбца, получим
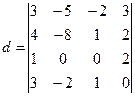
Умножим элементы первого столбеца на (-2) и сложим с элементами четвертого столбца, получим
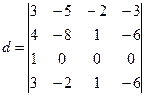
Вычислим определитель, разложив
его по ![]() строке
строке

2) Вычислим определитель, предварительно получив нули во втором столбце
Умножим элементы первой строки на (-2) и сложим с элементами третьей строки, получим
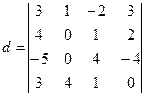
Умножим элементы первой строки на (-4) и сложим с элементами четвертой строки, получим
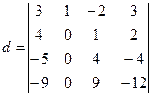
Вычислим определитель, разложив
его по ![]() столбцу
столбцу
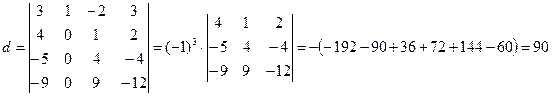
Задание 3.Найти общее решение для каждой из данных систем и проанализироватьее структуру (указать базис пространства решений однородной системы, установить размерность пространства, выделить частное решение неоднородной системы).
|
2в.
|
|
|
Решение:
1)
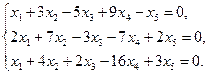
Теорема Кронекера-Капелли: Система совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы
Найдем ранг матрицы системы
![]()
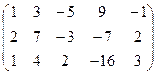
С помощью элементарных преобразований приведем ее к виду трапеции:
1 шаг: умножим первую строку матрицы на (-2) и прибавим ко второй, получим:
![]()
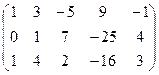
2 шаг: умножим первую строку матрицы на (-1) и прибавим к третьей, получим:
![]()
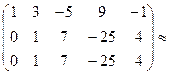
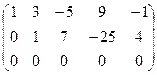
Очевидно, что ранг матрицы ![]() ,следовательно система не
совместна,
,следовательно система не
совместна, ![]() ,
, ![]() .
.
Система при ![]() является неопределенной.
является неопределенной.
Пусть ![]() -
базисная неизвестная,
-
базисная неизвестная,![]() - свободные неизвестные.
Заменим исходную матрицу системой
- свободные неизвестные.
Заменим исходную матрицу системой
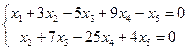
![]()
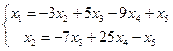
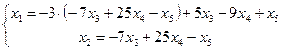
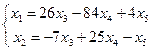
![]()
Пусть
![]() , тогда
, тогда ![]() ,
,![]()
пусть
![]() , тогда
, тогда ![]() ,
,![]()
пусть
![]() , тогда
, тогда ![]() ,
,![]()
Получена фундаментальная система решений
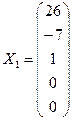 ;
;
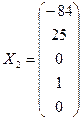 ;
;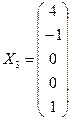
Общее решение системы можно записать в виде:
![]() ,
где
,
где ![]() - любые произвольные числа.
- любые произвольные числа.
2)
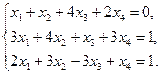
Найдем ранг матрицы системы
![]()
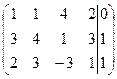
С помощью элементарных преобразований приведем ее к виду трапеции:
1 шаг: умножим первую строку матрицы на (-3) и прибавим ко второй, получим:
![]()
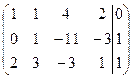
3 шаг: умножим первую строку матрицы на (-2) и прибавим к третьей, получим:
![]()
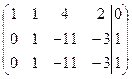 ;
;
4 шаг:умножим вторуюстроку матрицы на (-1) и прибавим к третьей, получим:
![]()
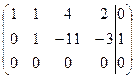 ;
;
![]()
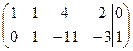
Очевидно, что ранг матрицы ![]() ,следовательно система не
совместна,
,следовательно система не
совместна, ![]() ,
, ![]() .
.
Система при ![]() является неопределенной.
является неопределенной.
Пусть ![]() ,
,![]() - базисные неизвестная,
- базисные неизвестная,![]() - свободная неизвестная.
- свободная неизвестная.
Заменим исходную матрицу системой
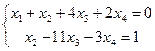
![]()
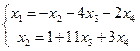
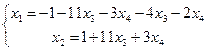
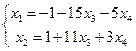
Пусть
![]() , тогда
, тогда ![]() ,
,![]()
пусть
![]() , тогда
, тогда ![]() ,
,![]()
Получена фундаментальная система решений
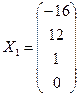 ;
;
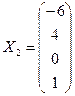
Общее решение системы можно записать в виде:
![]() , где
, где ![]() -
любые произвольные числа
-
любые произвольные числа
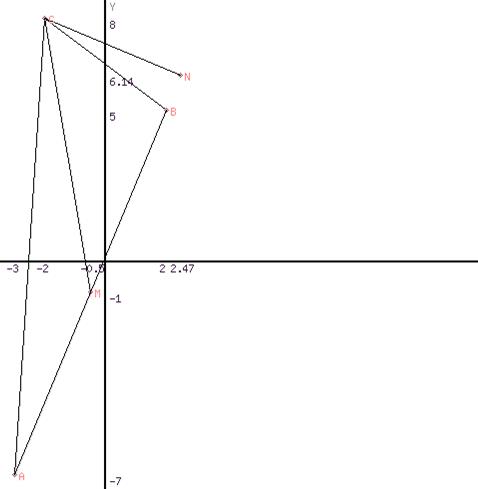
Задание 4.Даны координаты вершин треугольника АВС. Найти а) уравнение медианы и ее длину, уравнение высоты и ее длину, уравнение биссектрисы, проведенных из вершины С; б) уравнение прямой параллельной стороне АВ; в) угол А. Выполнить чертеж.
|
2 в. А (-3; -7); В (2; 5); С (-2; 8).
|
Решение:
1. Длины сторон определим по формуле
![]()
![]()
![]()
![]()
2. Уравнение сторон
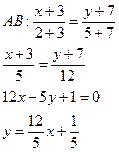
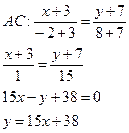
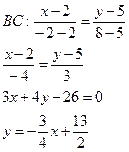
а) уравнение медианы и ее длину, уравнение высоты и ее длину, уравнение биссектрисы, проведенных из вершины С;
Медиана
Для нахождения уравнения медианы СМ найдем координаты точки М (середина отрезка АВ)
![]() .
.
![]()
Уравнение медианы СМнайдем используя формулу для
уравнения прямой, проходящей через две заданные точки. Медиана СМ
проходит через точки С (-2; 8) и ![]()
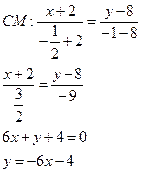
Найдем длину медианы, как расстояние между двумя точками С
(-2; 8) и ![]()
![]() , имеем
, имеем
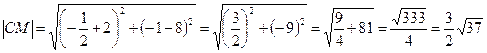
Высота
Для нахождения уравнения высоты СN найдем ее угловой коэффициент из условия перпендикулярности прямых СN и АВ.
Для стороны АВ имеем уравнение
![]()
Имеем ![]() .
.
Теперь используя формулу уравнения прямой, проходящей через
заданную точку ![]()
![]() , составим уравнение
высотыпроходящей через заданную точкуС (-2; 8)
, составим уравнение
высотыпроходящей через заданную точкуС (-2; 8)
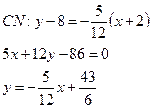
Длину высоты СNнайдем по формуле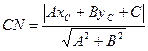 - расстояние от точки С до прямой
- расстояние от точки С до прямой ![]()
Имеем 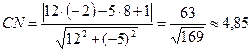 .
.
Биссектриса
![]()
![]()
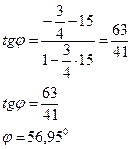
![]()
Угол ![]() тупой
тупой
Тангенс угла наклона ВС равен ![]()
Биссектриса проходит через точку С (-2; 8) , тогда по
формуле ![]()
![]()
б) уравнение прямой параллельной стороне АВ;
![]()
Уравнение прямой параллельной АВ определим по формуле
![]() , где
, где ![]()
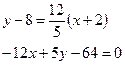
в) угол А
внутренний угол А определим по формуле
Уравнение ![]()
Уравнение ![]()
Угол ![]() между двумя
прямыми, заданными уравнениями с угловыми коэффициентами
между двумя
прямыми, заданными уравнениями с угловыми коэффициентами ![]() и
и ![]() вычислим
по формуле
вычислим
по формуле
![]()
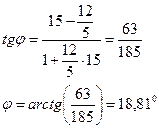
Выполним чертеж
Задание 5.Даны координаты вершин пирамиды. Средствами векторной алгебры найти:
1) объем пирамиды А1 А2 А3 А4;
2) длину ребра А2 А3;
3) площадь грани А1 А2 А3;
4) угол между ребрами А1 А2 и А1 А4;
5) угол между гранями А1А2А3 и А1А2А4;
6) уравнение высоты, проведенной из вершины А4 на грань А1А2А3 и ее длину.
7) выполнить чертеж.
2 в. А1 (4; 2; 5); А2 (0; 7; 2); А3 (0; 2; 7); А4 (1; 5; 0);
Решение:
1) объем пирамиды найдем по формуле:
![]() ,
где
,
где ![]() – смешанное произведение векторов,
исходящих из вершины пирамидыА1(4; 4; 10), которое вычисляется с
помощью определителя, составленного из координат этих векторов. Найдем
координаты векторов:
– смешанное произведение векторов,
исходящих из вершины пирамидыА1(4; 4; 10), которое вычисляется с
помощью определителя, составленного из координат этих векторов. Найдем
координаты векторов:
![]() ;
; ![]() ;
;![]()
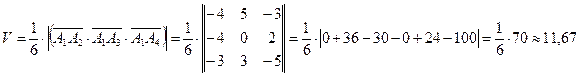
2)
длину ребра ![]()
Длину ребра ![]() определим по формуле
определим по формуле
![]()
![]()
3) Найдем площадь грани A1A2A3
![]() ;
; ![]()
![]()
Векторное произведение:
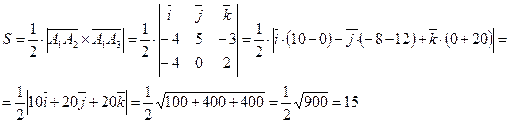
4) угол между ребрами А1 А2 и А1 А4
Найдем угол между ребрами ![]() ;
;
![]()
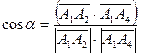
![]()
![]()
5) угол между гранями А1А2А3 и А1А2А4
Уравнение
плоскости ![]() найдем как уравнение прямой
проходящей через три данные точки А1 (4; 2; 5); А2 (0;
7; 2); А3 (0; 2; 7)по формуле:
найдем как уравнение прямой
проходящей через три данные точки А1 (4; 2; 5); А2 (0;
7; 2); А3 (0; 2; 7)по формуле:
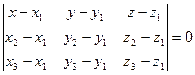
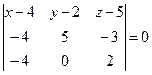
![]()
![]()
![]() - уравнение плоскости
- уравнение плоскости ![]() , ее нормальный вектор имеет
координаты
, ее нормальный вектор имеет
координаты ![]()
Уравнение плоскости ![]() найдем
как уравнение прямой проходящей через три данные точки А1 (4; 2;
5); А2 (0; 7; 2); А4 (1; 5; 0)
найдем
как уравнение прямой проходящей через три данные точки А1 (4; 2;
5); А2 (0; 7; 2); А4 (1; 5; 0)
по формуле:
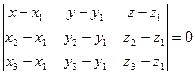
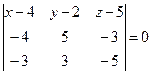
![]()
![]() - уравнение плоскости
- уравнение плоскости ![]() , ее нормальный вектор имеет
координаты
, ее нормальный вектор имеет
координаты ![]()
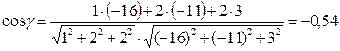
![]()
6) уравнение высоты, проведенной из вершины А4 на грань А1А2А3 и ее длину.
Прямая, проходящая через точку M0(x0;y0;z0)
и перпендикулярная плоскости![]() имеет
направляющий вектор (A;B;C).
имеет
направляющий вектор (A;B;C).
Уравнение плоскости A1A2A3:
![]() , координаты точки
А4 (1; 5; 0)
, координаты точки
А4 (1; 5; 0)
![]()
![]()
Длина высоты пирамиды, проведенной из вершины А4 (1;5;0).
Расстояние d от точки M0(x0;y0;z0)
до плоскости ![]() равно абсолютному
значению величины:
равно абсолютному
значению величины:
![]()
Уравнение плоскости A1A2A3:
![]() , координаты точки
А4 (1; 5; 0)
, координаты точки
А4 (1; 5; 0)
![]()
Чертеж
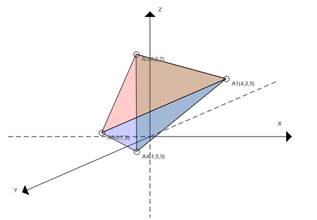
Задание 6 Найти область определения и построить графики функций.
|
2в |
а) б) |
|
|
|
|
|
|
|
|
Решение:
а) ![]()
Требуется найти область определения функции, для этого нужно знать области определения элементарных функций
Так как область определения
элементарной функции ![]()
![]() , то данной функции
, то данной функции ![]() ,
,![]() .
.
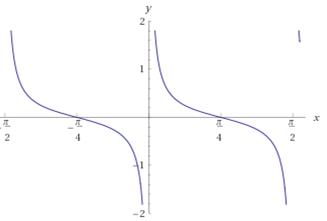
б) ![]()
Требуется найти область определения функции, для этого нужно знать области определения элементарных функций
Так как область определения
элементарной функции ![]()
![]() , то данной функции
, то данной функции ![]() ,
, ![]() .
.
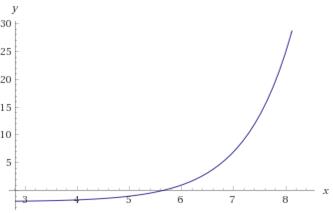
Задание 7Найдите пределы функций, не пользуясь правилом Лопиталя
|
2 в. а) |
в) |
д) |
|
б) |
г) |
Решение:
а) ![]()
Имеем неопределенность ![]() . Раскроем эту неопределенность,
поделив числитель и знаменатель дроби на
. Раскроем эту неопределенность,
поделив числитель и знаменатель дроби на ![]() :
:
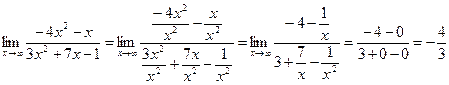
б) ![]()
Имеем неопределенность ![]() . Раскроем неопределенность
применяя первый замечательный предел
. Раскроем неопределенность
применяя первый замечательный предел ![]()
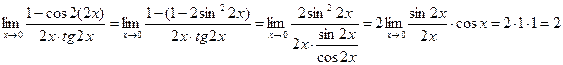
в) ![]()
![]()
г) ![]()
Имеем неопределенность ![]() . Раскроем эту неопределенность,
используя второй замечательный предел
. Раскроем эту неопределенность,
используя второй замечательный предел ![]()
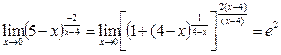
д) ![]()
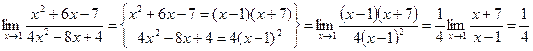
Задание 8Найти точки
разрыва функции ![]() и установить их
характер. Укажите односторонние пределы в точках разрыва. Построить график
функции
и установить их
характер. Укажите односторонние пределы в точках разрыва. Построить график
функции
|
2 в. |
Решение:
Функция ![]() определена на всей
числовой оси. Но из этого не следует, что она и непрерывна на всей числовой
оси, так как эта функция неэлементарная; она задана двумя различными формулами
для различных интервалов изменения аргумента
определена на всей
числовой оси. Но из этого не следует, что она и непрерывна на всей числовой
оси, так как эта функция неэлементарная; она задана двумя различными формулами
для различных интервалов изменения аргумента ![]() и
может иметь разрыв в точках
и
может иметь разрыв в точках ![]()
Исследуем функцию в точке ![]() , для этого найдем
, для этого найдем
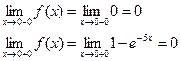
Функция определена, пределы слева и справа существуют и равны, следовательно
в точках ![]() функция
непрерывна;
функция
непрерывна;
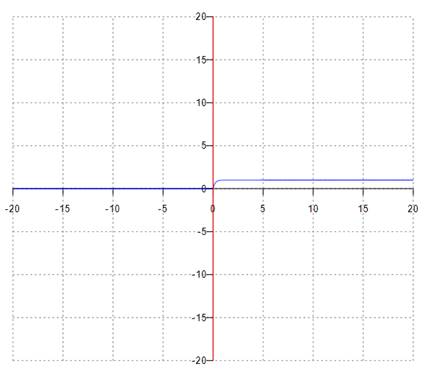
График
Задание 9Найти производные ![]() первого порядка данных функций
первого порядка данных функций
2 в. а) 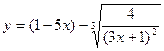 ; б)
; б)![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
д)
;
д) ![]() ;
;
Решение:
а) 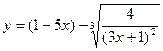
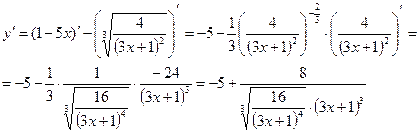
б) ![]()
![]()
в) ![]()
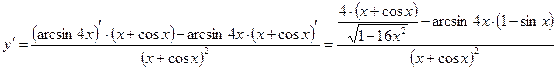
г) ![]()
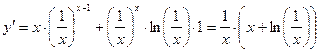
д) ![]()
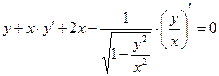
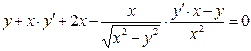
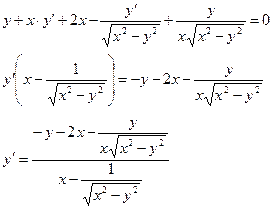
Задание10 Построить график функции у=f(x), используя общую схему исследования функции
|
2 в.
|
Решение:
1. Элементарные исследования
1) ![]()
2) ![]()
не симметрична; нечетная, ни нечетная.
3) ![]() предельное значение
предельное значение
4) существование асимптот:
а) вертикальных асимптот нет
б) ![]() - горизонтальная асимптота
- горизонтальная асимптота
в) ![]()
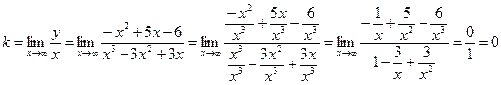 - наклонных асимптот нет
- наклонных асимптот нет
5) определить точки пересечения с осями координат:
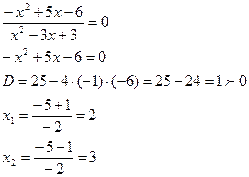
Пересечения с
осью Оx: ![]() ,
, ![]()
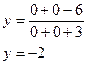
(0;-2) – точка пересечения с осью Оy
2. Исследования графика с помощью I производной
1)
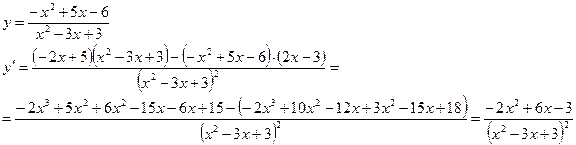
![]()
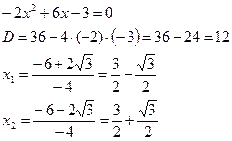
2) точки подозрительные на экстремум
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
0 |
- |
|
|
|
|
|
|
|
3)
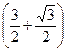 – максимум
– максимум
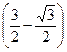 – минимум
– минимум
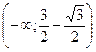
![]()
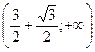 - график функции убывает
- график функции убывает
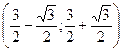 - график функции возрастает
- график функции возрастает
3. Исследования графика с помощью II производной
1)
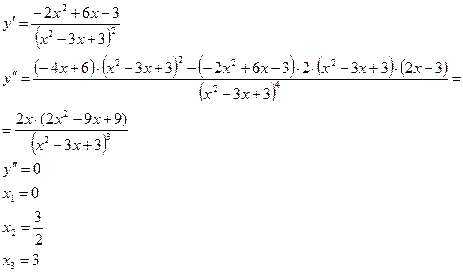
2) Точки подозрительные на перегиб
|
|
|
|
|
|
|
|
- |
+ |
- |
+ |
|
|
|
|
|
|
3)
![]()
![]() -
график вогнутый
-
график вогнутый
![]()
![]() - график выпуклый
- график выпуклый
4. По проведенным исследованиям строим график
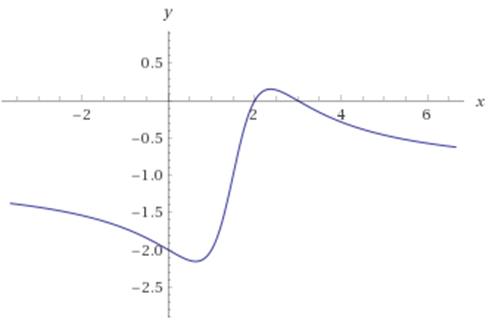
Задание 11.Изобразить комплексные числа z1,z2 на комплексной плоскости. Произвести указанные действия над комплексными числами и записать результаты в алгебраической, показательной и тригонометрической формах:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() 4)
4) ![]() .
.
|
2в |
|
![]()
![]()
![]()
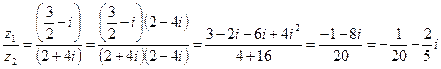
![]()
![]()
![]()
![]()
![]() =
=![]()
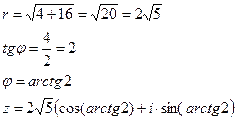
![]()
![]()
![]()
![]()
Учебно-методическое обеспечение дисциплины
Основная литература
- Стойлова, Л.П. Математика: учебник для студ. учр. высш. проф. образования / Л. П. Стойлова. – 2-е изд., перераб. и доп. – Москва: Издательский центр «Академия», 2012. – 464 с. – (Сер. Бакалавриат). – ISBN 978-5-7695-7970-7
- Редькин, Н.П. Дискретная математика : учебник [Электронный ресурс]. / Н.П. Редькин. - Москва : Физматлит, 2009. - 263 с. - ISBN 978-5-9221-1093-8;
- URL: http://biblioclub.ru/index.php?page=book&id=75709.
- Судоплатов, С.В. Дискретная математика : учебник [Электронный ресурс]. / С.В. Судоплатов, Е.В. Овчинникова. - 4-e изд. - Новосибирск : НГТУ, 2012. - 278 с. - (Учебники НГТУ). - ISBN 978-5-7782-1815-4; - URL: http://biblioclub.ru/index.php?page=book&id=135675.
5.2 Дополнительная литература
- Грес, П.В. Математика для гуманитариев: Общий курс: методическое пособие [Электронный ресурс]/ П.В. Грес . 2-е изд., перераб. и доп. –Москва: логос, 2009.-288с.-(Новая университетская библиотека).– ISBN 978-5-98699-113-9; Режим доступа: URL: http://biblioclub.ru/index.php?page=book&id=89783
- Пенчанский, С.Б. Основы начального курса математики в примерах и задачах : учебное пособие / С.Б. Пенчанский. - Минск : РИПО, 2018. - 240 с. : ил. - Библиогр. в кн. - ISBN 978-985-503-830-7 ; То же [Электронный ресурс]. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=497498
- Ельчанинова, Г.Г. Элементарная математика : учебное пособие [Электронный ресурс]. / Г.Г. Ельчанинова, Р.А. Мельников ; Минобрнауки РФ, Елецкий гос. университет им. И.А. Бунина. - Елец : Елецкий гос. университет им. И. А. Бунина, 2016. - Ч. 4. Геометрия. Начальные сведения. Треугольник. - 93 с. - Библиогр. в кн. - ISBN 978-5-94809-852-4. - ISBN 978-5-94809-853-1 (ч. 4) ; - Режим доступа: http://biblioclub.ru/index.php?page=book&id=498154
- Бережной, В.В. Дискретная математика : учебное пособие [Электронный ресурс]. / В.В. Бережной, А.В. Шапошников ; Минобрнауки РФ, ФГАОУ ВО «Северо-Кавказский федеральный университет». - Ставрополь : СКФУ, 2016. - 199 с. : ил. - Библиогр. в кн. ;– Режим доступа: http://biblioclub.ru/index.php?page=book&id=466802
- Пенчанский, С.Б. Основы начального курса математики в примерах и задачах : учебное пособие [Электронный ресурс]. / С.Б. Пенчанский. - Минск : РИПО, 2018. - 240 с. : ил. - Библиогр. в кн. - ISBN 978-985-503-830-7 ;– Режим доступа: http://biblioclub.ru/index.php?page=book&id=497498
- Баженова, Н.Г. Теория и методика решения текстовых задач: курс по выбору для студентов специальности 0500201 - Математика : учебное пособие [Электронный ресурс]. / Н.Г. Баженова, И.Г. Одоевцева. - 4-е изд., стер. - Москва : Издательство «Флинта», 2017. - 89 с. : табл., граф., схем. - ISBN 978-5-9765-1411-9; Режим доступа: http://biblioclub.ru/index.php?page=book&id=103321.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.