Жакатаев Т. А.
Физикалық химия, термохимия және коррозия теориясы негіздері
Основы физической химии, термохимии и теории коррозии
Basics Physical chemistry,
Termochemistry and corrosion theory
Нұр-Сұлтан қ., 2020 ж.
УДК 536.7
Физикалық химия, термохимия және коррозия теориясы негіздері.
Жакатаев Токсан Айыпханович, техника ғылымдарының докторы.
Рецензент: доктор химических наук, профессор каф. Радиофизика и электроника Физико-технического факультета КарГУ им. Е. А. Букетова, Бектурганов Жаналы Султанович.
Техникалық және жаратылыстану ЖОО, ООО студенттеріне, магистранттарға, докторанттарға, оқытушыларға арнайы және қосымша әдебиет ретінде арналған. Материал түсінікті, тәптіштелген, ғылыми терең, жеткілікті ауқымды, оригиналды түрде жазылған. Колледж студенттеріне, пәндерді тереңдетіп оқытатын арнайы мектептерге де пайдалы.
Для студентов, магистрантов, докторантов и преподавателей ВУЗов, студентов колледжей и учащихся специализированных школ с углубленным изучением предметов на казахском языке. Группа технических и естественно-фундаментальных специальностей.
For students, master 's students, doctoral students and teachers of higher education institutions, college students and students of specialized schools with in-depth study of subjects in Kazakh. Group of technical and naturalfundamental specialties.
ISBN ISSN
ББК
Физикалық химия, термохимия және коррозия теориясы негіздері.
Жакатаев Т. А., техника ғылымдарының докторы. [email protected]
Нұр-Сұлтан қ. 2020 ж.
Мазмұны
Параграф № бет
Кіріспе 6
Тарау 1. Молекулярлық физика негіздері 7
1. Газдар туралы алғашқы ұғым. 7
2. Бойль-Мариотт заңы. 7
3. Гей-Люссак, Шарль заңдары. 8
4. Абсолюттік температура. 12
5. Масса бойынша еселік қатынастар. Гей-Люссак,
Авагадроның бірінші заңы. 13
6. Авагадроның екінші заңы (1811). 14
7. Идеалды газдың күй теңдеуі. 16
8. Газ тұрақтысы. 18
9. Газдардың молекулярлық массасын
тығыздықтары арқылы анықтау 19 10. Дальтон заңы 20
11. Газдардың кинетикалық теориясы 21 12. МКТ бойынша қысымды есептеу. 22
13. Газ заңдарын МКТ дан шығару.
Орташа кинетикалық энергия. 24
14. Молекуланың хаотикалық қозғалысының энергиясын бостандық дәрежесі бойынша таралуы, бӛлінуі. Біркелкі бейтарап күй.
Газдардың жылу сыйымдылығы. 26
15. Термодинамиканың бірінші заңы. Жылу сыйымдылық. 29
16. Газдың кӛлемі ұлғайғандағы жұмыс 30
17. Пуассон формуласы. Адиабаталық процесс. 32
18. Политропалық процесс. 35 19. Политропалық, т. б. процесстердегі жұмыс. 37
20. Квазистатикалық процесс.
Қайтарымды, қайтарымсыз процесстер. 38
21. Жылу қозғалтқыш. Пайдалы әсерлік
коэффициент п.ә.к., к.п.д. 40 22. Термодинамиканың екінші заңы. 42
23. Карно циклы. 44
24. Карно теоремалары. 45
25. Клаузиус теоремасы. 48
26. Энтропия. 50
27. Қайтарымсыз процесстегі энтропия ӛзгерісі. 52
Тарау 2. Термодинамикалық потенциалдар теориясы.
Физикалық химия негіздері. 54
1. Термодинамиканың бірінші, екінші заңдары.
Біріккен термодинамиканың заңы. 54 2. Ішкі энергия және оның дербес туындылары 54
3. Энтальпия және оның туындылары 56
4. Гельмгольц функциясы. Изохорлы-изотермиялық потенциал. 57
5. Гиббс энергиясы. Изобарлық-изотермиялық потенциал. 59
6. Термодинамикалық потенциалдар және
механикалық емес жұмыс. 61 7. Гиббс-Гельмгольц теңдеуі. 64
8. Химиялық потенциал 65
9. Тепе-теңдік күйдегі жүйе. Гиббс-Дюамель теңдеуі. 68 10. Термодинамикалық потенциалдың қысым мен
температураға байланысы. 69
11. Ерітінділер термодинамикасы. Рауль заңдары. 74
12. Теормодинамиалық функциялардың (ТФ) ӛзгерістерін
анықтау. Энтропияға байланысты ӛзгеру бағыты. 78
13. Химиялық процесстерде ТФ қолдану. 83
Тарау 3. Химиялық тепе теңдік. 85
1. Әрекеттенуші масса заңы. Тепе теңдік константа. 85
2. Гомогенді реакциялардағы тепе теңдік заңдары. 92
3. Гетерогенді реакциялардағы химиялық тепе теңдік. 92
4. Химиялық реакцияға байланысты термодинамиканың
бірінші заңы. 97
5. V=const болғандағы химиялық
реакцияның жылулық эффектісі. 100
6. P=const болғандағы химиялық
реакцияның жылулық эффектісі. 100
7. 𝑄𝑃,𝑚𝑎𝑥 және 𝑄𝑉,𝑚𝑎𝑥 арасында байланыс. 101
8. Жанудың, заттың пайда болуының стандартты жылу мӛлшері.
Гесс заңы. 106
9. Есеп шығару үлгілері. 111
10. Реакциялардың жылу эффектінің
температураға байланысы. Кирхгоф заңы. 125
11. 𝑄 =𝑓(𝑇) функцияның түрі. 128
12. Есеп шығару үлгілері. 132 Тарау 4. Реакция бағытын болжау. 135
1. Тепе теңдік константа және диссоциация. 135
2. Тепе теңдік константаны эксперименталды
түрде анықтау. 141
3. Реакцияның атқаратын максималды
жұмысы және реакция константасы. 147 4. Жалпы түрде жазылған реакциялар. 151
5. Реакция бағыты. Тепе теңдік шарты. 154
6. Тепе теңдік константаның температураға байланысы. 156
7. Есептейтін теңдеулер. Есеп мысалдары. 158
Тарау 5. Гальваникалық элементтер теориясы 161
1. Мыс, қола, алтын элементтері. 161
2. Коррозияның химиялық негіздері. 162
3. Химиялық элементтердің, металлдардың стандарттық
электродтық потенциалдары. 163 4. Катодтық қорғау кезіндегі реакциялар. 166
5. Гальваникалық элементте тоқ және э.қ.к. қалай пайда болады. 170 6. Э.қ.к. химиялық энергия сақталу негізінде есептеу. 173
7. Zn пластинасындағы паразиттік тоқ. 174
8. Электродтар поляризациясы . 175
9. Гальваникалық элементтердің деполяризациясы. 177
10. Аккумуляторлар 178
11. Электрлік қозғалтқыш күш э.қ.к. 179
12. Ом заңы 181
Әдебиет 183
Кіріспе
Физикалық химия, термохимия және коррозия теориясы негіздері инженерлік мамандықтардың маңызды пәні болып табылады. Қозғалтқыштардың п.ә.к. есептеу, бу, газдардың, сұйықтардың физикалық, химиялық қасиеттерін білу – болашақ инженерге маңызды. Қайтарымсыз және қайтарымыды термодинамикалық процесстерде энтропия, Гельмгольц, Гиббс функциялары ӛзгеріп және тӛмендеп отырады. Оларды есептеу арқылы процесстің қай бағытта жүретінін, болатынын болжайды. Бумен немесе жанған газ қысымымен қозғалатын газды турбиналарды есептегенде, энергия сақталу заңында энтальпия мен энтроропия қолданылады. Идеалды газдың күй теңдеуі, заңдары, молекулярлық кинетикалық теория негіздері, әртүрлі процесстердегі жасалған жұмыс, т.б. кӛптеген қызықты және ӛндірістік практикада аса маңызды сұрақтармен танысасыздар.
Техникалық процесстерде сан алуан химиялық реакциялар жүріп жатады, қарапайым заттардан басқа күрделі заттар пайда болады. Сондағы жылулық, пайда болу эффектілерді есептей білу кәзіргі инженерге ӛте маңызды. Осында Гесс заңдары және оның салдарлары үлкен роль атқарады. Күрделі жүйедегі химиялық реакциялар тепе-теңдік күйге түседі. Тепе теңдік константасын есептей білу маңызды. Сол бойынша реакция бағытын да болжайды.
Термодинамикалық функцияларды есептегенде парциалдық қысым, активтілік, фугитивтілік сандары, коэффициенттерінің рӛлі, орны теориялық түрде негізделген және кӛрсетілген.
Термодинамикалық функциялардың шектік және шекаралық жағдайдағы температураға байланысты функция ретіндегі рӛлі айқын, нақты кӛрсетілген. Температураға байланысты функцияның интегралдау константасы ретінде атқаратын рӛлі де кӛрсетілген.
Кӛптеген әдебиеттердің ішінен физикалық, термо химияның нәтижелерін аспап, құрал жасау технологиясында пайдаланғандары бар.
Ең жақсы оқытушы – ол практика. Сондықтан кӛптеген есептердің шешімдері тәптіштелген түрде жазылған.
Соңғы тарауда коррозия теориясы, соған байланысты электрлік химиялық процесстер тәптішті түрде баяндалған. Аккумуляторлы жүйеде
э.қ.к. қалай пайда болатыны баяндалған.
Кітап бакалавриат, магистратура, докторантурада оқитындарға арналған. Сонымен қоса оқытушы-профессор қауымына да арналады. Кӛптеген сұрақтар ғылыми тұрғыдан тиянақты, түпкілікті баяндалған. Оригиналды, ерекше, жаңаша жолмен талданған жерлері бар. Осы бағыттағы кітаптар жинағы жалғасады деп үміттенеміз.
Ғылыммен техниканың қандай да болмасын сұрақтары шексіз тереңге кете береді. Ешбір автор осы жазғаным – толық бәрін қамтиды деп айта алмайды. Сондықтан қажетті жерде оқырмандарға жақсы, пайдалы болады дегендей, әдебиет тізімі ұсынылған. Қосымша есептер шығару үлгілері және үй тапсырма ретінде беруге болатын есептер [1-3] әдебиеттерде жеткілікті кӛлемде бар. Осы кітаптар djvu, pdf электронды форматтарда кең тараған. Сондықтан сілтеме жасаумен ғана шектелуге болады. Бізбен хабарлассаңыздар осындай электронды форматтағы кітаптармен бӛлісуге әзірміз.
Оқырмандарға сәттілік тілейміз. Пікірлеріңізді келесі электронды адреске жіберуге болады [email protected], рахмет.
Тарау 1. Молекулярлық физика негіздері
П. 1. Газдар туралы алғашқы ұғым.
Ғылым мен техникада газ бен сұйықтар кеңінен қолданады. Сондықтан сұйықпен газдың күйлерін, олардың физикалық қасиеттерін сипаттайтын теңдеулерді білу маңызды болып табылады. Ең әуелі газдарды қарастырайық. Идеалды газда әрбір молекула (немесе атом) басқа молекулалармен ӛзара әсерлеспейді, яғни әсерлесу арқылы туындайтын потенциалды энергия болмайды. Олар бір бірімен соқтығысқанда тек қана кинетикалық энергиямен ғана алмасады. Яғни механикалық түрде ғана әсерлесу болады. Соқтығысқанда тек қана импульстармен ғана алмасады. Молекулалары бір бірімен ӛз ара алыстан әсерлесетін газды реалды газ деп атайды. Ондай газдың молекулалары бір біріне жақындағанда, соқтығысу серпімді (упругий) болмайды. Оларда әсерлесудің потенциалды энергиясы болады. Және де сол потенциалды энергия ӛзгермелі функция. Кӛп факторге байланысты болады.
П. 2. Бойль-Мариотт заңы.
1662 ж. Р. Бойль, одан тәуелсіз Э. Мариотт 1667 ж. формула (1) кӛрсеткен заңдылықты тапты. Температура және масса тұрақты болған
кезде 
.
(1)
Немесе қысым кӛлемге байланысты тура кері прапорционал ӛзгереді
.
(2)
(1) және (2) келесі түрде де жазылады.
.
(3)
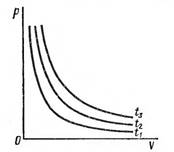
Сурет 1 – Бойль заңы. Изотермалар.
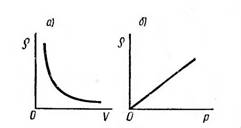
Сурет 2 – тығыздықтың кӛлемге және қысымға байланысы
Сурет 1 – де 
. P = P (V)
функциясын кері пропорционалды тәуелділік дейді. 2 сурет а) да
тығыздықтың кӛлемге, б) да
тығыздықтың қысымға тәуелділігі
кӛрсетілген. 1-ші суретте кӛрсетілген графиктер
изотермалар.
П. 3. Гей-Люссак, Шарль заңдары.
Қысым және масса тұрақты болғанда (P=const, m=const) температура ӛзгергенде кӛлем соған байланысты сызықты түрде ӛзгереді
,
(1)
Ж. Л. Гей-Люссак заңы (1806 ж.) да
Бойль-Мариотт заңы сияқты эксперимент арқылы
анықталған. 
0C
сәйкес кӛлем.
Изобаралық процесске жатады.
Тәжірибе жасағанда (1) ді келесі түрде пайдаланған жӛн
,
(2)
мұнда t-температура 0С, 
0С,
-
газдың кӛлемінен, қысымынан, құрамынан,
температурадан тәуелді емес, ол тұрақты шама, 
– ол t = t0
= 0 болғандағы бастапқы кӛлем.
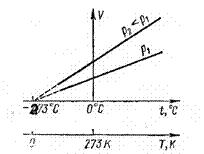
Сурет 1. Кӛлемнің температураға байланысты ӛзгерісі
(1) мен (2) дегі тәуелділік сурет 1-де
кӛрсетілген. Кӛлем температураға байланысты сызықты
ӛседі. Қысым кішірейгенде ӛсу темпі ұлғаяды. Оны
ӛсу коэффициентінің мәні ұлғайғаны
арқылы байқауға болады: 
.
- эксперименталды анықталатын
коэффициент, ол тең
.
V=V(t) түзу сызығын t - ның минус
жағына жалғастырса, кӛлем кішірейе береді және 
0C
болғанда V= 0 болады. Бұл мүмкін емес, себебі зат - материя
бар болғанда оның кӛлемі жоқ болып, ноль болып
кетпейді. Сондықтан 
0C жетпейтін,
физикалық реалды ӛмірде болмайтын, жетуге мүмкін емес, реалды
емес температура. Осы температураны абсолюттік ноль деп атайды. Сондықтан
жаңадан Кельвин температура шкаласы пайда болды –T. Кельвин температура
шкаласын абсолюттік температура шкаласы дейді. Оның басы, нольдік
мәні 
сәйкес болады 
, сурет 1.
Температура ӛскенде кӛлем ӛсетінді келесі приборда
кӛруге болады, сурет 2. Колбада ауа. Жінішке трубка колбамен
жалғасқан. Трубканың горизонталды жағында
сынаптың тамшысы бар. Колбаның ішінде қысым ӛскенде
сынаптың тамшысы оң жаққа жылжиды. Кӛлемнің
ӛскенін кӛрсетеді. Колбаның сыртында стакан. Онда су.
Судың температурасы ӛскенде колбаның ішіндегі ауаның да
температурасы ӛседі.
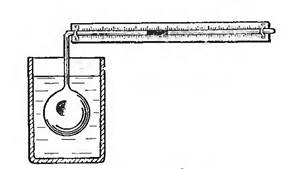
Сурет 2. Гей-Люссак эксперименті.
V=0 болғандағы 
0C екенін нақты
дәлелдейік. Сонда
(2) ден шығады
.
(3)
(3) тен болады
C. (4)
Цельсий шкаланы абсолюттік температуа шкаласымен ауыстыруға болады
.
(5)
(5) ті (2) ге қойғанда болады
,
.
(6)
Мұндағы тұрақты тек қысымға ғана тәуелді, температураға байланысты емес. (6) келесі түрде жазылады
.
(7)
(2) мен (7) Гей-Люссак заңының екі түрлі жазулары.
Сол сияқты қысымға да (1)-ге ұқсас теңдеулер орынды екені тәжірибеде дәлелденген (V=const, m=const)
.
(8)
Мұнда 
-
прапорционалдық коэффициент. (8) ді P=P(t) функциясы 3 суретте
кӛрсетілген.
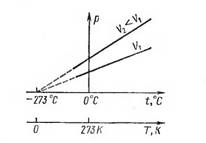
Сурет 3. Ж. Шарль заңы.
0С , сондықтан (8) ді
келесі түрде жазады
.
(9)
Кӛлем температураға байланысты сызықты ӛседі. Кӛлем кішірейгенде функцияның ӛсу темпі ұлғаяды. Оны ӛсу коэффициентінің мәні
ұлғайғаны арқылы
байқауға болады: 
. Эксперимент кӛрсеткендей
.
P=P(t) түзу сызығын t - ның минус
жағына жалғастырса, Қысым кішірейе береді және 
0C
болғанда P=0 болады. Бұл мүмкін емес, себебі зат - материя
бар болғанда оның қысымы жоқ болып, ноль болып
кетпейді. Сондықтан 
0C жетпейтін,
физикалық реалды ӛмірде болмайтын, жетуге мүмкін емес, реалды
емес температура. Осы температураны абсолюттік ноль деп атайды. Кельвин шкаласы
туралы жоғарыда айттық. Оның басы, нольдік мәні 
-
ге сәйкес болады 
, сурет 3.
P=0 болғанда 
0C
болатынын нақты дәлелдейік.
(9) дан шығады
.
(10)
(10) қайтадан болады
.
Яғни біз 
екенін
дәлелдедік. Кӛлем мен қысымның кеңею
коэффициенттері бірдей, бір сан. Бұл әрине қызық
факт.
(5) ші формуланы (9) ға қойғанда шығады
,
.
(11)
Сонымен, кӛлем тұрақты болғанда қысым абсолюттік температураға пропорционалды ӛзгереді. Қысым тұрақты болғанда кӛлем абсолюттік температураға прапорционалды ӛзгеререді.
.
(12)
(9) бен (12) Ж. А. Шарль заңы, 1787 ж.
табылған. 
сәйкес
қысым. Ол изохоралық процесс.
Гей-Люссак, Бойль – Мариотта, Шарль заңдары эксперименталды түрде дәлелденген, байқалған. Эксперимент кез келген кӛлемдегі және массадағы газдармен жасағанда орынды
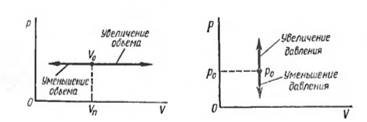
Сурет 4. Изобара, изохора.
П. 4. Абсолюттік температура.
Абсолюттік температура алғашқысында
газдар заңдарын ыңғайлы, ықшам түрге келтіру
мақсатында еңгізілген. Алайда, оның орны ерекше, физика,
жартылыс ғылымында ғылымында рӛлі маңызды, сыры
тереңде жатыр. Мысалға 
аумағында, кӛлем 
,
теріс мәнге ие болады. Ал физикалық тұрғыдан бұл
мүмкін емес жағдай. Теориялық және жалпы физикада
қарастырылатын Нернст теоремасы бойынша, абсолюттік ноль (Т=0) болмайтын
температура, оған жету мүмкін емес. Абсолюттік температура
механикалық қозғалысты, оның ішінде кинетикалық
энергияны сипаттайды. Абсолюттік нульде механикалық
қоғалыстар болмайды. Тек қана “нольдік тербелістер” болады.
Абсолюттік температураның осы бір ерекше рӛлін (қасиетін)
әйгілі орыс ғалымы М. В. Ломоноcов “Крайняя степень холода” деп
айтып ӛткен (1747).
П. 5. Масса бойынша еселік қатынастар. Гей-Люссак,
Авагадроның бірінші заңы.
Қарапайым (элементарлы) зат пен химиялық элемент арасында айырмашылық бар. Қарапайым элементарлы зат, мысалға темір. Оның ӛзіндік физикалық және химиялық қасиеттері болады. Орысша простое вещество. Темір күкіртпен қосылғанда ол физикалық, химиялық қасиеттерін жоғалтады. FeS темір сульфидінде темір элемент ретінде бар. Яғни атом ретінде. Элемент дегеніміз – атом дегеніміз. Сол сияқты темір сульфидінде күкірт те атом-элемент ретінде бар. Химиялық элемент сонымен – атомдар. Олардың белгілі бір қасиеттері болады. Бір элементтің атомдары қосылып зат пайда болғанда – оны қарапайым зат, простое вещество дейді.
Әртүрлі элементтер әртүрлі қатынаста қосылғанда әртүрлі заттар пайда болады. Мысалға кӛміртегі оттегімен екі түрлі зат құрайды: CO, CO2 . Кӛмір оксидінде, кӛмір қышқылында масса бойынша кӛміртегі - 42,88 %
, оттегі – 57,12 % болады. Кӛмірдің диоксидінде, екі еселік оксидінде Кӛміртегі – 27,29 %, оттегі – 72,71 %. Осыдан Дальтон заңы: әртүрлі элементтер әртүрлі заттарда бір-біріне әртүрлі массалық қатынаста болады. 1 кестеде кӛрсетілген. Сонда екі заттағы құрамдық проценттік қатынасты бір – біріне бӛлсе – натуралды сан шығады.
Кесте 1
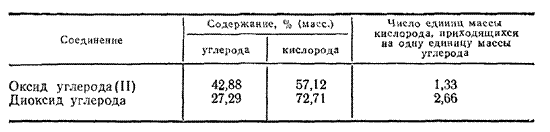
Дальтон заңы заттардың жекеленген атомдардан тұратынын дәлелдейді, сонымен түсіндіреді. Дальтон теориясында сутегі атомының массасы 1 деп қабылданды. Басқа элементтердің массасы осыдан еселік ретінде есептелді.
Дальтон заңын математикалық түрде дәлелдеуге болады. A, B – екі элементті қарастырайық. Олар AB және AB2 – екі зат құрастырады.
Олардың массаларын да осы әріптермен белгілейік A – бірінші элементтің массасы, кг, B – екінші элементтің массасы, кг Сонда
.
(1)
, 
- ӛлшемсіз
(безразмерная) масса. Сонда
.
(2)
Гей-Люссак әртүрлі газдардың химиялық реакцияға түскендегі кӛлемдерін зерттеді. Содан кӛлемдерге байланысты еселік қатынастар заңын тапты. Қысыммен температура тұрақты болғанда, реакцияға түсетін газдардың кӛлемдері бір-біріне, және жаңадан пайда болатын заттардың кӛлемдеріне қарапайым бүтін сандар болып келеді.
.
(3)
(2) ден газдардың кӛлемдері бір біріне қатынасады 1:3:2.
(2) -(4) тен Авагадро шығарды: температурамен қысым ӛзгермей, тұрақты, бірдей тең болғанда, кӛлемдері тең газдарда молекулалар саны да бірдей болады.
.
(4)
Осы Авагадроның бірінші заңы бір моль газдың кӛлемін, универсалды әмбебап газ тұрақтысын анықтағанда ӛте маңызды роль атқарды. Әдебиетте Авагадро заңдары бірінші, екінші деп жеке бӛліп айтылмайды. Екеуі де жәй Авагадро заңы делінеді. Шатастыру болмас үшін біз осы екі заңдарды бірінші және екінші деп бӛлек айтуды жӛн кӛрдік.
П. 6. Авагадроның екінші заңы (1811).
Авагадроның екінші заңы: қысым мен температура тұрақты (ӛгеріссіз) болғанда бірдей кӛлемдегі әртүрлі газдарда бірдей (тең) молекулалар саны болады.
12C изотопының
12 грамм мӛлшеріндегі атомдар саны Авагадро саны 
болып табылады.
Құрамында 
атомдар (не молекулалар) саны бар газ
(зат) кӛлемін бір моль дейді. Бір мольдың массасын M болсын.
P мен Т тұрақты болғанда әртүрлі газдардың бір моль-ы бірдей кӛлемде болады. Нормальды жағдайда: t0=0 0C, T0=273,13 K, P0 = 760 мм.сын.бағ.= 101325 Па болғанда бір моль газдың кӛлемі тең
𝑉0=22,415 л. (1)
(1)-ді дәлелдейік. Эксперимент арқылы
нормальды жағдайда бір литр 𝑂2
оттегінің салмағы 𝑚1
=1,43 г екені анықталған. Сонда бір мольдың
кӛлемі 
болады.
Бір моль газдағы молекулалар санын Авагадро тұрақтысы (саны) деп атайды
𝑁А =6,023∙1023 1/моль.
1961 жылы салыстырмалы атомдық массаның бір шкаласы қабылданған. 12С кӛміртегі изотопы атомының 1/12 бӛлігінің массасы 1 м.а.б. деп аталған, бір массалық атомдық бірлік. Басқа заттардың атомдарының массасын осы 1 м.а.б. ке қатынасы бойынша анықтайды. Сол бойынша оттегінің салыстырмалы (кӛп жағдайда бұл сӛзді айтпайды) атомдық массасы 𝐴𝑟 = 15,9994, ал су тегінің атомдық массасы 𝐴𝑟 = 1,00794. Яғни элементтің атомдық массасы тең 𝑚𝑎 =𝐴𝑟 ∙1 м.а.б.
Сол сияқты салыстырмалы молекулалық масса 𝑀𝑟 (қысқаша молекулалық масса) заттың молекуласының массасының 1 м.а.б. қатынасы. Молекуланың абсолюттік массасы тең 𝑚𝑀 =𝑀𝑟 ∙1 м.а.б. , 1 м.а.б.=1,667∙10−27 k𝑔. Мұнда 𝑀𝑟 - молекуланың салыстырмалы атомдық массасы.
Mольдық масса 𝑀𝑟 ға пропорционал екені айқын
𝑀 =𝐾∙𝑀𝑟. (2)
K –барлық заттарға бірдей коэффициент. 12C
затына 𝑀𝑟 =12.
Анықтама бойынша кӛміртегі үшін 
. Осыдан 𝐾 =1 екені
дәлелденеді.
Сутегі атомының 𝐴𝑟 =1,0079. Сутегінің бір молекуласы үшін 𝑀𝑟 =2,0158. Сонда бір моль 𝐻2 молекуласының мольдық массасы тең
.
Оттегі 𝑂2
молекуласының мольдық массасы тең
.
Сол сияқты басқа химиялық элементтердің мольдық
массалары химиялық кестедегі нуклондар саны бойынша анықталады. (2) формула – маңызды.
Оттегі 
кӛлемінің
килограмм-мольдық (молекулалық) шамасы = 32 кг/кмоль,
қысқаша кг-моль, 
– атомының килограмм –
атомдық шамасы = 16 кг/кмоль. Қысқаша кг-атом. СГС
жүйесінде грамм-молекула бірлігін пайдаланады. Оттегі молекуласы 
кӛлемінің
грамм – молекулалық шамасы = 32 г/моль. Ӛстіп кг-моль, грамм-моль
(грамм - молекула) салмақ бірліктері, мӛлшерлері
анықталады.
Кез келген атомның массасы = 1,66·10-27·
кг,
кез келген молекуланың массасы = 1,66·10-27·
кг.
Сұйықтағы молекуланың
размерін анықтайық. Сұйықта молекулалар бірбіріне
ӛте жақын, тығыз орналасқан. Сондықтан 1 киломоль
сұйықтың 
кӛлемін 
санына бӛлгенде
– бір молекула кӛлемі шығады. Судың бір киломолі = 18 кг.
Соған сәйкес 
0,018 м3.
.
Осыдан молекуланың сызықты размері шамамен болады
.
Басқа сұйықтардың да молекулалары размері Ангстреммен ӛлшенеді.
П. 7. Идеалды газдың күй теңдеуі.
Бастапқыда газдың параметрлері P,V,T
болсын. Соңғы, екінші күйдегі параметрлерді 
, 
, 
.
1 ден – 2-ге ауысуды екі қадаммен жасайық, яғни арасында
тағы бір күйді қарастырайық. Яғни бірінші
қадамда P →
ауысқанда Т = const болсын. Сонда
Бойлдың заңы бойынша
.
(1)
Яғни 
- 1 мен 2 арасындағы,
ортадағы күй, оны 1’ күй деп белгілейік. 1’ →2
ауысқанда, 
болсын. Сонда
.
(2)
(2) ден болады
.
(3)
(3) ті (1) ге қоямыз, сонда болады
.
(4)
Тұрақты 𝑟 (P,V,T) – лардан тәуелді емес. Бірақта ол газдың массаға, моль санына тәуелді болуы мүмкін. P, T –тұрақты болғанда Авагадро заңынан шығады
.
(5)
𝑛1, 𝑛2 - бірінші, екінші кӛлемдегі моль сандары. Ал (4) ті былайша жаза аламыз
,
(6)
.
(7)
(5) – (7) шығады
.
(8)
Мұнда r2 ≠r1 екенін дәлелдеу үшін (4), (6), (7) маңызды. Солай болады тек (7) де P2 =P1 , T2 =T1 болғанда ғана. Яғни (4), (6), (7) - формулалардағы 𝑟 - газдың мӛлшерінің қатынасына тәуелді. (8) ден жаңа тұрақты шығады
.
(9)
Сондықтан кез келген моль саны бар газ үшін газдың күй теңдеуі болады
𝑃𝑉 =𝑛𝑅𝑇 . (10)
Бір моль газ үшін келесі түрде жазылады
𝑝𝑉𝜇
=𝑅𝑇.
(11) Мұнда 
1 моль газдың кӛлемі, R –
универсалды газ тұрақтысы.
(10) ды келесі түрде жазады
.
(12)
(10) - (12) практикалық есептер шығарғанда жиі қолданады. 𝑚 - газдың массасы, кг, 𝜇 - газдың бір мольдық массасы, кг/моль. Бір моль газдың массасын молярлық, немесе мольдық масса деп атайды. Осы дәлелдеу жолын кері жолмен жүргізуге болады. Бірінші, бір мольге (11) алады. Сонда (4) тегі r ді r=R деп дереу (11) қарастырады. Содан Авагадро заңынан және стандартты жағдайдағы қысыммен кӛлемнен – дереу R дің сандық мәнін табады. Одан кез келген мӛлшерлі газге (12) орынды дей салады. Нақты келесі параграфта айтылған.
П. 8. Газ тұрақтысы.
Универсалды газ тұрақтысын алғаш анықтағанда бұрынғы техникалық ӛлшем бірліктерді пайдаланған және СГС. Техникалық ӛлшеулерде ауа қысымы атмосферамен ӛлшенген. 1 атм = 760 мм.сын. бағ. , t = 0 oC. Температура t=4 oC болғанда 1000 г. судың кӛлемі 1 литр деп алынған. Сонда абсолюттік температура тең 𝑇0 =273,15 𝐾, 𝑃0 =1 атм болғанда бір мольдің кӛлемі тең 𝑉0 =22,415 литр. Сонда
= 0,082062 
.
(1)
(1) ді абсолюттік СГС жүйесінде есептейік. Сонда 𝑝𝑜 =1,01325∙
106 дин/см2, 𝑉0 =2,2415∙104 см3. Сонда
Эрг/К.
1 Эрг = 2,3892 ·10−8 Кал, сондықтан
𝑅 = 8,3148 ∙107 ∙ 2,3892 ·10−8 =1,9866 кал/К (2)
1 кал = 4,19 Дж, сондықтан
𝑅 =1,9866 ∙4,19=8,3148 Дж/К. (3)
(3) ті (1) формула арқылы дереу, тікелей, жылдам Си жүйесінде шығаруға болады
.
(4)
Сонда (1) мен (2) – ол тарихи шығару жолы. (4) – кәзіргі Си жүйесі бойынша дереу, жылдам шығатын жол.
Кейбір техникалық жылдам және
жуықтау есептеулерде 𝑅
=2 кал/К немесе 𝑅
= 0,082 
деп қабылдайды.
П. 9. Газдардың молекулярлық массасын
тығыздықтары арқылы анықтау
m кг газдың V м3 кӛлемі
болсын. 
тығыздық болады кг/м
моль саны. 𝜇 -
бір мольдың салмағы, молярлық (мольдық) салмақ
дейді, кг. 𝑚 -
газдың жалпы салмағы. 
- мольдық кӛлем, бір
мольдың кӛлемі, м3/моль. 
. Қалыпты
жағдайда 𝑉0 =
22,415 · 10−3
м3. Осыдан
μ=22,415 · 10−3 ∙ρ (1)
(1) формула қолданбалы есептерде маңызды. Сонымен молярлық салмақ тығыздық арқылы анықталады.
Кӛп жағдайда газды заттардың тығыздығын ауаның 𝜌в немесе су тегінің 𝜌н тығыздықтарына байланысты салыстырмалы түрде анықтайды
.
Ауаға μВ =28,98, су тегіне μ𝐻 =2,016 г/моль. Сондықтан кез келген газға орынды
𝜇 =28,98∙𝐷𝐵 , 𝜇 =2,016∙𝐷𝐵 . (2)
(2) формула практикада қолдануға ыңғайлы. Себебі салыстырмалы тығыздық барлық газдарға жоғары дәлдікпен ӛлшенген. Реньо әдісінде бір ыдысқа газды сонсон ауаны кезекпен толтырып салмағын ӛлшейді. Кӛлем белгілі, қысым тұрақты. Гей – Люссак әдісінде кӛлемі белгілі, тұрақты ыдыстағы газдың (немесе будың) қысымын ӛлшейді. Майер әдісінде қысым белгілі, тұрақты, кӛлемді ӛлшейді. Осы әдістердің барлығында газдардың тығыздығы нормальды мәнге келтіру керек.
Ӛлшеу мәндеріне газдардың идеалды еместігі әсер етеді. Дегенмен бұрынғы классикалық әдістер кейінгі заманау әдістермен салыстарғанда жақсы дәлдікті кӛрсеткен. Осыны 1 кестеден кӛреміз [10]. Онда мольдық массалар келтірілген.
Кесте 1
П. 10. Дальтон заңы
Әртүрлі газдарды бір ыдысқа толтырса, онда олар толық араласып кетеді. Ортақ бір қысым орнайды. Қаншама араласса да газдарды идеалды деп есептейік. Яғни олардың молекулалар арасында әсерлесу жоқ. Осындай жағдайда Дальтон заңы орынды. Сол бойынша кӛп құрамды газдар бар ыдыста қорытынды жалпы қысым барлық газдардың парциалдық қысымының қосындысына тең. Парциалдық қысым – ол жекеленген бір газ сол ыдыста жалғыз ӛзі болғандағы қысым.
.
(1)
Мұнда
-
(2)
бір газдың парциалдық қысымы.
, ... , 
.
(3)
(1)-(3) тен шығады
.
(4)
-
жалпы грамм-молекула саны, жалпы моль саны. Парциалдық қысым тең
.
П. 11. Газдардың кинетикалық теориясы
Газдардың қасиетін (қысым) кәдімгі механика заңдарынан түсіндіруге арналған ғылыми бағыт – газдардың кинетикалық теориясы деп аталады. Осы салада Бернулли (1738), Ломоносов (1746), Клаузиус, Максвелл, Кельвин (19 ғасыр) үлкен жетістіктерге жеткен. Молекулярлық кинетикалық теория МКТ – деп аталған. Алайда теормодинамиканың екінші заңы (екінші бастамасы) осы механикалық қозғалыс негізінде түсіндіріле алмаған. Екінші заңда да молекуланың қозғалысы маңызды роль атқарады. Сол үшін қосымша, ықтималдық теория негізіндегі заңдылықтарды теорияға пайдалану , қосу керек болды. Сӛйтіп теормодинамикада статистикалық әдістер пайда болды.
Термодинамикада статистикалық әдістерді Больцман, Гиббс бастады. Ол үлкен ілімге, ғылымға, мықты құралға айналды.
МКТ қарапайым бірнеше қарапайым принципте негізделген. Принцип дегеніміз – қабылданған белгілі бір қағида, кӛзқарас.
Біріншіде газ молекулалары шар тәрізді, біркелкі, соқтығысқанда абсолютті серпімді, упругий шар ретінде қарастырылады. Соқтығыс механиканың абсолютті серпімді соқтығыс заңымен сипатталады. Екіншіде молекулалар (шарлар) үнемі қозғалыста болады, тепловое движение, жылулық қозғалыс. Бір бірімен соғылғанша молекулалар түзу сызық бойымен қозғалады.
Үшіншіде. Шарлар қозғалысы кеңістікте жан жаққа шәшіраңқы, бейберекет бағытталған. Бір шамадағы кеңістіктегі стерадиан бойынша орташа молекула саны да бірдей, шамамен тең болады.
Бір атомды газдың барлық жылулық энергиясы оның поступательный кинетикалық энергиясына тең. Поступательный - тек кеңістікте орын ауыстырумен сипатталатын қозғалыс. Айналу жоқ. Молекулалардың поступательный қозғалысының жылдамдығы ӛте жоғары болады. Оны кесте 1 ден кӛреміз. Орташа жылдамдықтың аса жоғары мәндеріне қарамастан молекулалардың кеңістіктегі диффузиясы ӛте жәй, тӛмен болады. Мысалға ашылған одеколон иісін біраз уақыттан сон ғана сеземіз. Ол молекулалардың ӛзара аса кӛп соқтығысатының себебі. Бір молекула орта есеппен бір секундта бір миллиардтқа дейін соқтығыс кӛреді. Екі соқтығыс арасында 10-5 см жол жүреді.
Кесте 1
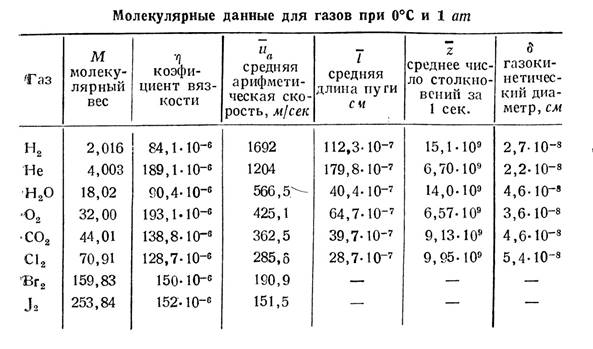
МКТ негізінде үш маңызды заңдар қорытылып шығады, тӛменде.
П. 12. МКТ бойынша қысымды есептеу.
Қабырғаға әсер ететін
қысымды есептейміз. Ол 1 секунда ішінде 1 см2
қабырға ауданына қаншама молекула (шар) келіп соғылады,
соған байланысты. V кӛлемде N молекула бар, кубтың бір
қырының ұзындығы L, 1 сурет. Молекулалардың
орташа квадраттық жылдамдығы 
, (1) ші формула.
(ABCD) қырға әсер ететін P қысымды табамыз. Ол
молекулалық кинетикалық теория (м.к.т.) бойынша жасалды. Орташа
квадраттық жылдамдықты - орташа арифметикалық
жылдамдықтан ажырата білу керек, (1), (2) формулалар. Себебі осы
теорияда орташа жылдамдықтардың квадратының
қосындысының орташа мәні алынады
.
(1)
.
(2)
Молекула қабырғаға
соғылғанда +m
береді. Қабырға оны кері
серпіп ұшырғанда қосымша мынандай импульс қабылдайды -m
.
Сонда бір молекуланың қабырғаға берген жалпы импульсы
тең болады
.
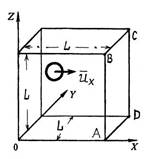
Сурет 1. Қабырғаға қысымды есептеу.
(ABCD) ауданға
1 секундта молекулалар соғылып импульс береді. Орташа қысымды 1
секундта қабырғаға соғылған молекулалардың
сол қабырғаға берген қозғалыс мӛлшері
(импульс) арқылы есептейді. 
, ,
- молекуланың координат осьтері
бойынша жылдамдықтың проекциялары. 
- бір секундта бір
қабырғаға әсер ететін соқтығыс саны. Сонда
бір секундада берілген жалпы импульс тең
.
(3)
- күш,
ӛлшем бірлігі, Н. Молекулалар кеңістік бойынша бейтарап
бағытталған, бейберекет қозғалады. Әрбір
бағыттар бір біріне тең құқылы. Осыдан
.
.
(4)
N/V = n молекула санының кӛлемдік
тығыздығы. 
уақытта бір молекула L
ұзындықты жүріп ӛтеді. (ABCD)
қабырғаға бір молекула екі рет соғылғандағы
арасындағы уақыт тең 
. Ал 1 секунда
уақытта бір молекула сол қабырғаға
(5)
рет соғылады. Яғни мынандай мӛлшерде
(6)
жалпы соқтығыс (удар) болады. Сонда (3) тең болады
.
(7)
(7) ні келесі түрде жазамыз
.
(8)
(8) ші формула V
кӛлемдегі барлық N молекула 1 секунда уақытта (ABCD)
қабырғаға беретін импульс мӛлшері, қозғалыс
мӛлшері. Импульс бӛлінген уақыт болады күш. Яғни 
-
күш, Н. Кӛлем тең
.
(9)
(9) ды (8) ке қойғанда болады
.
(10)
P - (ABCD) қабырғаға әсер ететін жалпы қысым, Па.
(10) формуланың сәл ӛзгешелеу қорыту жолы бар. Сонда әуелі бір молекуланың қабырғаға әсер етуші күшін есептейміз. (3)-(5) формуладан шығады
.
(11)
Қорытынды күшті табу үшін барлық N молекула бойынша қосамыз
. (12)
(12) формула (7) мен бірдей. Одан арғы қорытынды белгілі. (6) – да әуелі бір секундадағы жалпы соқтығыс саны есептеледі. Содан барып сон жалпы күш есептеледі. Ал (12) де әуелі бір молекуланың бір секунда уақыттағы әсер етуші күші есептеледі. Содан сон барып барлық молекулалар бойынша әсер етуші қорытынды күш есептеледі. Айырмашылық осында. Алайда екеуі де соңында бір нәтиже береді. Мәселені екі еселік интегралды есептеумен салыстыруға болады. Мысалға бірінші жағдайда әуелі X бойынша интегралдап алып, содан сон сыртқы интегралды Y бойынша есептейді. Екінші жағдайда әуелі Y бойынша, содан сон барып X бойынша интеграл алады. Айтқанымыздай нәтиже біреу, (10) шы формула.
П. 13. Газ заңдарын МКТ дан шығару.
Орташа кинетикалық энергия.
(10-10) келесі түрде жазайық
.
(1)
-
(2)
жалпы кинетикалық энергиясы, N- барлық молекулалардың саны. (2) ні
(1) қоямызда жазамыз
.
(3)
(3) ті (6-10) мен салыстырамыз. Сонда
.
(4)
Мұнда 
– моль саны, 
-
Авагадро саны.
(2) мен (4) ден бір молекуланың кинетикалық энергиясын табамыз
,
(5)
– Больцман тұрақтысы. (5)
тің физикалық
мазмұны бар - жекеленген молекуланың
кинетикалық энергиясын абсолюттік температура арқылы
ӛрнектейді. Немесе, температура орташа кинетикалық энергиянық
мӛлшері дейміз. (5) бойынша 
= 0 болады, сонда
қозғалыс болмайды деп ойлап қалуға болады. Алайда,
қозғалыс мүлде тоқтап қалмайды. Абсолдюттік
нольде барлық заттар кристалдық түрде болады, ал молекулалар
“нольдік тербелісте болады”. Алайда кӛптеген себептермен нольдік
температураға жетуге мүмкін емес, недостижимо. Асимптоталық
түрде жақындайды. Әзірше 
K жеткен.
(3) пен (4) ті келесі түрде жазамыз
.
(6)
(6) дан Дальтон заңы қорытылып шығады, себебі
,
.
(3) пен (4) тен газ заңдары (Бойль-Мариотта, Шарля, Гей-Люссака) қайтадан шығады. Сол үшін P,V,T – үш функцияның кезектесіп біреуін тұрақты дей отырып, қалған екеуінің бір-біріне тәуелді деп қарастыру керек. Сонда МКТ газ заңдарын толық негіздейді деп айтамыз.
П. 14. Молекуланың хаотикалық қозғалысының энергиясын бостандық дәрежесі бойынша таралуы, бӛлінуі. Біркелкі бейтарап күй.
Газдардың жылу сыйымдылығы.
Идеалды газдың молекулалары бір бірімен қашықтан әсерлеспейтін нүкте, немесе абсолютті серпімді упругий шар ретінде қарастырылады. Яғни бір бірімен әсерлесетін потенциалды энергия жоқ. Серпімді соқтығыста жалпы импульс жоғалмайды. Қабырғаға соғылса, қандай импульспен келді, сондай импульспен кері қайтады. МКТ негізінде (11-5) формуласын қарастырайық. Ол үш ӛлшемді кеңістікте келе жатқан молекуланық энергиясы. Кеңістік үш координат осімен сипатталады X,Y,Z. Әрбір бағыт, әрбір координат осі – тең құқылы. Яғни жекеленген бір коорднат осі бойынша таралатын кинетикалық энергия болады
,
(1)
i=x, y, z. Осы үш координатаны үш еркіндік дәрежесі дейміз (степень свободы). Молекуланың размері үлкен, немесе формасы симметриялы емес болуы мүмкін. Мысалға гантель тәрізді, немесе үш бұрышы бар пирамида. Мұндайда сол молекула белгілі бір нүкте орталығынан, немесе осьтен айналып тұрады. Сонда инерция моментін ескеру керек. Себебі айналу процесі жүріп жату үшін, оған да энергия керек. Әрбір айналу осін, немесе айналу нүктесін (центрін) – жеке дара бостандық дәрежесі (степень свободы) дейміз. Сонда әрбір бостандық дәрежеге (1) дегідей энергия кетеді. Бұл Джеймс Максвеллдің тұжырымы. Мысалға молекула (шар) бір ось бойынша айналып жатса, және бір ось бойынша поступательный қозғалыста болса, қорытынды энергиясы тең болады
.
(2)
Бір степеньде кинтетикалық және потенциалдық энергия бар делік. Осы екі энергия қосылып жанағы бір степеньге беретін жалпы энергия ол да (2) ге тең болады. Молекулада поступательный, айнымалы және тербелмелі энергиялар болсын. Сонда жалпы энергия тең
.
(3)
- поступательный
(жылжымалы), айнымалы (вращательный), тербелмелі (колебательный)
қозғалыстардың дәреже (степень) саны. Кейіннен
білінді, әрбір степеньге энергия тең бӛліну заңы тек классикалық
физикада ғана орынды екен. Энергия үзіліссіз ӛзгергенде.
Квантово механикалық кӛзғараста бұл принцип
орындалмайды, немесе жуықтап қана орындалады. Максвелл ол туралы
білген жоқ, ол кезде кванттық теория әлі болған
жоқ. Тербелістің аса жоғары жиіліктерінде
,
аса кіші кеңістікте, мысалы атом ішіндегі немесе
кристаллдық тор ішіндегі қозғалыстарда, аса кіші T нольге жуықтайтын температурада кванттық эффектілер болады.
Классикалық жуықтауда, газдарды идеалды дей отырып жылу сыйымдылықты табуға болады. Жылу берудің әртүрлі жағдайына байланысты жылу сыйымдылық та ӛзгереді. Кӛлем тұрақты болғанда келген жылу тек қана ішкі энергияның ӛсуіне жұмсалады
.
Сол кезде молярлық жылу сыйымдылық
. (4)
Молекула тек 3 дәрежелі поступательный қозғалыста болсын. Сонда мольдық жылу сыйымдылық тең
Дж/(моль·К).
Бір атомды газдың молярлық жылу сыйымдылығы температураға байланысты емес.
Екі атомды қатты (жестко) байланысқан молекуланы қарастырайық. Гантель тәрізді молекула дейміз. Гантель үш ось бойынша айнала алады X,Y, Z. Яғни оның 3 айнымалы дәрежесі болады. Әрбір дәрежеге келетін энергия
,
мұнда 
- оське байланысты инерция моменті, 
-
айналу жылдамдығы. гантельдің ұзындығы бойынша
бағытталған осьтегі иенция моменті кіші шама. Сондықтан
соған сәйкес бұрыштық айналу жылдамдық ӛте
жоғары болады. Сондықтан екі атомдық газдың
молярлық жылу сыйымдылығы тең
Дж/(моль·К).
(5)
Бірақта тәжірибе
бойынша осы жылу сыйымдылық тең 
. Яғни
жоғарғы мәнді айнымалы жылдамдыққа байланысты
дәреже роль атқармайды, болмайды. Тӛменгі температураларда
жылу сыйымдылық 
- ге дейін тӛмендейді. Жоғары
температуларда 3R ден асып кетеді.
Сондықтан атомдар арасында әсерлесудің потенциалды энергиясы бар дейміз. Олар қосымша бостандық дәрежесін тудырады. Айтылған ерекшеліктер сонымен байланысты. Яғни қосымша бостандық дәрежелері қосымша энергия таралуын тудырады. Жылу сыйымдылық артады.
Кӛп атомды молекулаларда үш поступательный, үш айналатын, бірнеше тербелістік дәрежелер болу керек. Тербелістік – атомдар арасында тербеліс пайда болады. Сондықтан кӛп атомды молекуланың мольдық жылу сыйымдылығы 3R ден әлде неше кӛп болады. Жылу сыйымдылықтың температураға байланысты ӛзгерісі кванттық заңдылықтармен ғана сипатталады. Сол бойынша ең минималды энергия ӛзгерісі, энергия кванты тең
,
- тербелетін толқынның
жиілігі, 
Дж·с.
Тӛменгі температураларда тербеліс және айналу қозғалыстар азаяды. Соған сәйкес еркіндік дәрежелер істен шыға бастайды, орыс әдебиетінде степени “вымораживаются” дейді. Планк – Эйнштейн формуласы
.
(6) Әдеттегі температурада тербелістегі энергияға 
< kT.
Тек жоғары температурада ғана 
~ kT. Осыны
дәлелдеу үшін (6) ны 
𝜈
қатарына
𝑘𝑇
жіктейміз. Сонда
= kT.
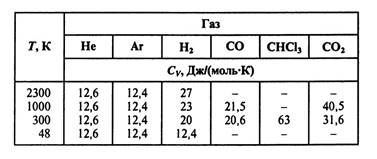
Кесте 1 де әртүрлі газдарға молярлық жылу сыйымдылық келтірілген
С𝑉.
Кесте 1.
П. 15. Термодинамиканың бірінші заңы. Жылу сыйымдылық.
Газға берілген жылу мӛлшері екі нәрсеге жұмсалады: 1 - ішкі энергияның ӛзгеруі, 2 - газдың жұмыс жасауына
𝛿𝑄 =𝑑𝑈+𝛿𝐴. (1)
(1) -термодинамиканың бірінші заңы. Газға жылу алмасу арқылы берілген жылу мӛлшері 𝑑𝑄, Дж. Таза жылу алмасу процесінде жасалған жұмыс ескерілмейді. 𝑑𝑈 - ішкі энергияның ӛзгеруі. 𝛿𝐴 - газдың жасаған жұмысы. Ол кӛлемнің ұлғаюына байланысты, Дж. Жылу сыйымдылық тең
.
(2)
Ӛлшем бірлігі [c] = [Дж/(кг·К)]. Кӛп жағдайға бір мольге қатысты жылу сыйымдылықты қарастырады
,
(3)
[C] = [Дж/(моль·К)]. Кӛлем тұрақты болғанда жұмыс жасалмайды,
𝛿𝐴=0. Дәлелі келесі п. 14-те. Сол кезде (1) ші формула бойынша
.
(4)
Қысым тұрақты болғанда жылу сыймдылық коэффициенті тең
.
(5)
.
(6)
(5) пен (6) дан шығады
𝑅 =𝐶𝑃 −𝐶𝑉. (7)
(7) бір моль үшін орынды.
Дәлірек айтсақ (3) ті мына түрде жазуға болады
,
мұнда 𝑛 - моль саны. Кӛп жағдайда 𝑛 ді жазбайды.
П. 16. Газдың кӛлемі ұлғайғандағы жұмыс
Газдың кӛлемі ұлғайғандағы жұмыс тең
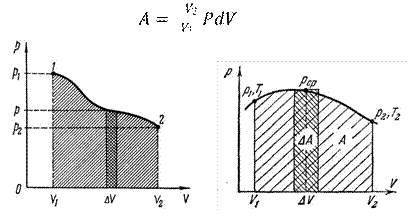. (1)
Сурет 1 – Газдың кӛлемі ұлғайғандағы жұмыс
(1) ді дәлелдейміз. Қысым тең [Па]
(2)
F – күш, Н, S – аудан, м2 . Негізі жұмыс тең
,
(3)
-жүрген жол,
траектория, м. (2) ні (3) ке қоямыз да, (1) ді табамыз. Интеграл (1) ді
жуықтап жазамыз
.
Мұнда 
.
Изобаралық процесстегі жұмыс тең
.
(4)
Изотермиялық процесстегі жұмысты табайық.
Сонда
.
(5)
(4) ті (1) ге қоямыз.
.
(6)
(6) – бір мольдың жұмысы. Кез келген мӛлшердегі газге болады
.
(7)
Адиабата процесі. Осында жүйе ( яғни
кӛлемдегі газ) сыртқы ортаға жылуды бермейді, және
қабылдамайды да. Яғни 
(1) ден шығады
.
(8) Минус таңба адиабаталық кеңеюде ішкі энергия
азайғанын кӛрсетеді. Кеңею жұмысы ішкі энергияның
азаю салдарынан болады. Адиабаталық сығылу кезінде жұмысты
сыртқы күш жасайды, ол поршеньды ішке жылжытады. Сонда 
≥
0 оң таңбалы. Және 
0 теріс мәнді. (1) ші формула
бойынша кӛлем кішірейіп жатыр деген сӛз.
Бір моль газге байланысты адиабаталық процессті қарастырайық.
Сонда (13-4) формуладан
.
(9)
=const, 
деп
интегралдағанда
.
(10)
(8), (9) дан адиабаталық процесстегі жұмыс шығады
. (11)
П. 17. Пуассон формуласы. Адиабаталық процесс.
(14-10) да қысымды 
деп жазайық,
сонда
.
(1)
Осыдан
.
Сонда
.
Немесе
.
(2)
(13-7) бойынша
.
(3)
Мұнда
Пуассон коэффициенті. (2) мен (3) тен шығады
.
(4)
Келесі түрлерде жазады
.
(5)
Немесе
.
(6)
(5), (6) – Пуассон формуласы, идеалды газдардағы адиабаталық процесске орынды. Пуассон заңынан шығады: газ адиабаталық кӛлемін ӛсіргенде, температурасы тӛмендейді, салқындайды. Газ адиабаталық түрде кӛлемі кішірейгенде, температурасы ӛседі, қызады.
Адиабаталық процесс орынды болу үшін газдың сыртқы ортамен жылу алмасуы мүлде болмау керек. Ал изотермалық процессте газдың сыртқы ортамен жылу алмасуы шексіз жоғары және жылдам болуы керек. Әрине осы екі жағдай реалды (тәжірибелік) жағдайда орынды болмайды, ол – абстракция. Дегенмен реалды процесстер изотермаға сонсон адиабатаға жуықты түрде ғана орынды болуы мүмкін. 1) газдың кӛлемі ӛте аз уақыт ішінде күрт ӛзгереді. 2) Ӛте үлкен массалы газ кӛлемін ӛзгертеді. Осы екі жағдай адиабатаға жуықтап келеді. Сыртқы ортамен жылу алмасу салыстырмалы түрде ӛте аз болады. Іште жану қозғалтқышындағы (двигатель внутреннего сгорания) процессті, велосипед камерасын үрлеу процесстерін адиабата деп есептейді. Массасы үлкен кӛлемдегі (массасы үлкен) газдың адиабаталық кеңею процесін қарастырайық, 15-1 суретте кӛрсетілген. а – үлкен егістік алаң, пашня, с-тоғай, b – су бассейні.
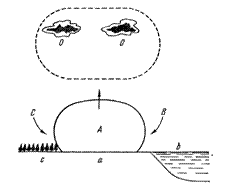
Сурет 1. Үлкен массадағы адиабаталық процесске мысал
Күннің кӛзінен егістік алаң а қызады. А кӛлемдегі үлкен массалы ауа температура айырмашылығы арқасында жоғары аспанға кӛтеріледі. С, В кӛлемдегі ауа салқын болғандықтан тӛменге түседі. А кӛлемінде жоғары кеткен ауаның орнын толтырады. Солай жоғары жылжитын үлкен массалы ауа ағыны пайда болады. Жоғары биіктеген сайын атмосфералық қысым азая түседі. Содан А кӛлемдегі ауаның кӛлемі ұлғая береді, ауа кеңейіп бара жатқан ағыншаға ұқсайды, похожа на струю с расширением. Осы адиабаталық кеңею негізінде А кӛлемдегі ауа температурасы тӛмендейді, салқындайды. Температура шық нүктесіне жеткенде, су буы конденсация болады. Сӛйтіп шоғырланған бұлттар, кучевые облака О пайда болады. Осындай бұлттарды “жақсы күнгі”, “ашық күнгі” бұлттар деп атайды.
Пуассон теңдеуіне қайта оралайық. Клапейрон-Менделеев теңдеуі бойынша
.
(7)
(7) ны (6) ке қоямыз
.
Осыдан болады
𝑃𝑉𝛾 =𝑐𝑜𝑛𝑠𝑡. (8)
Мұнда 𝑅∙𝑐𝑜𝑛𝑠𝑡 =𝑐𝑜𝑛𝑠𝑡. (8) Пуассон теңдеуінің екінші түрі.
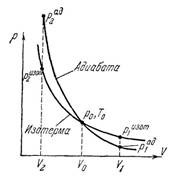
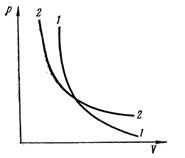
Сурет 2. 1-адиабата Пуассона. 2 – Бойль-Мариотт заңы.
Сурет кӛрсеткендей адиабата тіктеу, круче болады.
П. 18. Политропалық процесс.
Политропалық процессте
𝑃𝑉𝑛 =𝑐𝑜𝑛𝑠𝑡, (1)
мұнда 𝑛 - политропа кӛрсеткіші. Политропалық процесс бұрынғы процесстердің бәрін дербес жағдай ретінде қамтиды, 1 кестеде
кӛрсетілген
кесте 1
Оның ішіне бәрі кіреді: изобара, изотерма, адиабата, изохора. n – ӛзгереді осыдан -∞ , дейін +∞. Кестедегі бірінші 3 жол айқын кӛрінеді. Тӛртінші жолды дәлелдейік. Сол үшін (1) ді келесі түрде жазамыз
𝑃1𝑉1𝑛 =𝑃2𝑉2𝑛 . (2)
1, 2 – индекстер кез келген әртүрлі екі күйге арналған. n ретті түбір аламыз
1 1
.
(3)
(3) те
ұмтылады 
немесе 
, сонда болады
.
(4)
(4) – изохорлық процесске сай. Идеалды газдың күй теңдеуінен
.
(5)
(5) ті (1) ге қойғанда болады
.
(6)
(6) T-V – координатадағы политропа теңдеуі деп аталады.
Бір моль газдың политропа процесіндегі жылуын табайық. (15-1) формула бойынша
Cондықтан
.
(7)
туындысын (6) дан табамыз. Сонда болады
.
(8)
(5) –ті (8)-ге қойғанда болады
.
(9)
(9)-ды (7)-ге қойғанда болады
.
(10)
(10) формулада P, V, T параметрлер жоқ. Сондықтан политропадағы жылу сыйымдылық тұрақты болады. Яғни жылу сыйымдылық тұрақты болғандағы процесстерді политропалық процесс деп анықтауға болады. Немесе басқаша, жылу сыйымдылық кӛлемге, қысымға, температураға тәуелді емес болғанда – политропалық процесс дейміз. Политропалық процессті ӛстіп анықтағанымыз, (1) , (2) формуламен анықтағаннан гӛрі толықтау, дәлдеу болады. (10) негізінде анықтағанымызда газ,сұйық, қатты дене – бәріне келеді. Ал (1) негізінде анықтағанымыз – тек газдарға ғана келеді. (10) дан политропа кӛрсеткіші шығады
.
(11)
П. 19. Политропалық, т. б. процесстердегі жұмыс.
Жұмыстың формуласы (16-1)
. (1)
(18-2) былай жазамыз
.
(2)
(2) ден P
.
(3)
(3) ті (1) ге қоямыз
.
(4)
Бірінші 
жағдайды қарастырайық.
Сонда интеграл болады
.
(5)
(5) ті (4) ке қоямыз, болады
.
(6)
(6) ны түрлендіру үшін келесі формуланы пайдаланамыз
.
(7)
(7) ні (6) ға қоямыз, болады
.
(8)
(6), (8) кез келген политропалық процесстегі жұмысты кӛрсетеді. Тек изотермалық жағдайды қамтымайды n=1. Мысалға адиабаталық жағдайда жұмыс тең болады
.
(9)
Изотермалық процесстегі жұмыс былай анықталады
.
.
(10)
Изобаралық жұмыс тең
.
(11)
Изохоралық процессте жұмыс нольге тең.
П. 20. Квазистатикалық процесс.
Қайтарымды, қайтарымсыз процесстер.
Термодинамикада газдың кӛлемінде әрбір нүктеде P, T, ρ тұрақты деп есептеледі. Күй бірқалыпты, равновесный. Бір процесс болса бірқалыпты күй бұзылады. Мысалға поршень аз ғана сығылды, 16-1 сурет.
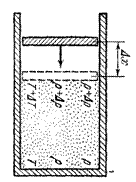
Сурет 1. Бірқалыпты күйдің бұзылуы.
Поршеннің қасындағы жерде параметрлер ӛседі. Біраз уақыттан сон параметрлер түгел кеңістікте теңеседі, бірқалыпты күй қайтадан орнайды. Осы уақытты релаксация уақыты 𝜏р дейді. Поршеньді аса баяу түрде не ішке не сыртқа жылжытайық. Асықпай қозғалтайық 𝜏р ≫∆𝜏 – поршеннің бір реттегі жылжыған уақыты. Сонда әрбір поршеннің қозғалысында қалыпты күй болып тұрады. Мысалға ыдысты тігінен қойып, поршень үстіне ұсақ құмның бір бір түйіршік тасынан үстінен салып, не алып тастап отыруға болады. Әрбір сығылу актісі бірқалыпты күйден болады. Осындай процессті квазистатикалық дейді. Квази – соған қатты ұқсайды, тақайды деген латынша сӛз. Қатарынан кӛптеген бірқалыпты (равновесный) күйден ӛтетін процессті квазистатикалық процесс дейді.
Изобаралық, изотермалық, изохорлық процесстерді квазистатикалық болып ӛткізу қиын емес. Олардың жылдамдығы шектелмейді, солай істеуге мүмкіндік береді. Адиабаталық процессті квазистатикалық қылу қиын болады. Бір жағынан жылу алмасу болмау үшін ол процес тез ӛту керек. Екінші жағынан 𝜏р ≫∆𝜏 болу үшін аса тез ӛткізу мүмкін емес.
Сондықтан тәжірибелік процесстерді жуықтап қана әрі адиабаттық, әрі квазистатикалық дей аламыз.
Қайтармалы процесc:
1) ол екі бағытта бірдей жүре алады. Кӛлем ұлғаяды, сонсон кішірейеді. 2) екі бағытта процесс жүргенде жүйе және сыртқы орта бірдей күйлерден ӛтеді. Процесс оңға сонсон солға жүргенде фазалық траектория ӛзгермейді, 16-2 сурет.
3) Алға сонсон кері процесс жүріп болғанда газ, дене және сыртқы орта (екеуі біріккенде-жүйе) бастапқы күйге оралады.
Осы 3 шарттың біреуі бұзылса процесс қайтарымды болмайды, становится необратимым. Үшеуі бірдей орындалса – процесс қайтарымды, обратимый.
Консервативті күш әсер еткендегі процесс қайтарымды болады. Мысалға вакуумдегі маятниктің тербелісі, абсолютті серпімді пружинадағы дененің тербелісі қайтарымды процесс.
Квастатикалық жылу алмасу процесі де қайтарымды болады. Газ квазистатикалық және изотермалық жолмен кӛлемін ∆𝑉 ұлғайтты. Жүйе әрбір уақытта квазистатикалық күйден ӛтіп отырды, сондықтан параметрлері бірқалыпты режимде қайтадан процесті кері ӛткізуге болады, яғни кӛлем бастапқы мӛлшерге кішірейеді.
Газ изотермалық түрде кӛлемін үлкейткенде 𝑄𝑇 =𝐴𝑇 жылу қабылдады. Осы жұмыстың арқасында поршеньде тұрған бір дене жоғары h кӛтеріліп, потенциалдық энергиясын ӛсірді 𝑄𝑇 =𝐴расш=mgh.
Кері процесс жүргенде дене тура сол h деңгейге тӛмен түседі. Дененің потенциалдық энергиясы газдың кӛлемін ∆𝑉 сығуға кетеді. Сонымен газдың изотермиялық кӛлемін ұлғайту және содан сон кішірейту процесстері жүргенде газ сонсон сыртқы орта (жүйе) диаграммада бір күйлерден ӛтіп отырды. Сондықтан квазистатикалық изотермиялық процесс – қайтарымды. Қайтарымды процесске келтіру – ол идеализация. Практикада кӛп процесстер қайтарымсыз. Мысалға жылу алмасу процесстері ӛте баяу болмайды, олар кәдімгідей жылдам ӛтеді. Сондықтан оларды сирек жағдайда ғана квазистатикалық деп атауға болады. Келесі мысал – диффузия процессі. Екі бӛлікте бӛлініп тұрған әртүрлі газдар бӛлуші перегородканы алып тастағанда араласады. Бұл процесс қайтарымсыз. Осыны диффузия процесі дейді. Яғни диффузия бір бағытта жүретін процесс, қайтарымды емес.
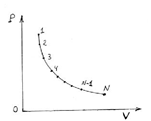
Сурет 2. Қайтарымды процесс
2 суретте қайтарымды процесс кӛрсетілген. 1,2,3, ... , N-1, N – бірінші, оңға бағыттағы күйлердің нүктелері. Екінші, солға бағыттағы процесс кезінде N, N-1, … , 3, 2, 1 – күйлердің нүктелері қайталанады, тура сол жолмен жүреді. 1 нүктеде аяқталады.
П. 21. Жылу қозғалтқыш. Пайдалы әсерлік
коэффициент п.ә.к., к.п.д.
Барлық жылу қозғалтқыштар газдың, отынның ішкі энергиясын сыртқы ортада жасайтын пайдалы механикалық жұмысқа айналдырады. Мысалы ішкі жану қозғалқышында жанғыш газдың химиялық жану энергиясы үлкен қысым тудырады. Сол қысым поршеньді итереді. Ядролық реакцияда бӛлінген атомнық бӛлшектері үлкен кинетикалық энергияға ие болады. Кинетикалық энергия тежегішті қатты қыздырады. Оның ішіндегі су қатты қызады, жоғары температураға және үлкен қысымға ие болады. Содан сон осы энергия будың аса қуатты жоғары қысымдағы, жоғары температурадағы ішкі жылу энергиясына айналады. Үлкен қысымдағы будың кинетикалық энергиясы содан сон бу турбинаны айналдырады. Теориялық тұрғыдан құр газдың (химиялық процессіз, жану болмайды) ішкі энергиясы ӛсіп 𝑈2 (термостаттан, сырттан қосымша жылу алып) соның салдарынан ӛз бетінше кӛлемі ұлғаяды. Сӛйтіп, поршеньді итергендей, механикалық жұмыс жасайды.
Газ салқындап, ішкі энергиясын тӛмендеткенде, сыртқы ортаға жылу береді. Ішкі энергия бастапқы 𝑈1 күйге келеді.
Біраз кеңейіп, кӛлемін ӛсірген газ содан кейін қайта сығылып алғашқы бастапқы күйіне келеді. Содан сон жұмыс істеу циклы қайтадан жүріп газ кеңейеді. Сӛйтіп барлық жылу қоғалғыш машиналар циклдік (айналып келіп,қайталанып) жобамен жұмыс жасайды.
Реалды жылу қоғалтқыштар разомкнутый (айырылған) циклмен жұмыс жасайды. Бастапқы пайдаланған газ ауаға мүлде шығып кетеді. Орнына газдың жаңа порциясы келеді. Осындай айырмашылыққа қарамастан, (P,V), (T,S) жүйелерде осы процесстерді айналымды (круговой) диаграммамен қарастыруға болады
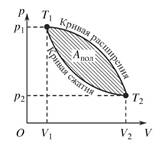
Сурет 1. Қозғалтқыштағы газдың жұмысының айналмалы диаграммасы
Жылу қозғалтқыштың энергетикалық балансын қарастырайық. Схемалық шартты түрде. Ол үш бӛліктен тұрады: 1) энергия кӛзі, жылуды беретін құрылғы, нагреватель, қыздырғыш. Ол газды белгілі, тұрақты бір температураға 𝑇1 қыздырып отырады. 2) пайдалы жұмыс жасайтын дене, орган, рабочее тело. 3) пайдаланбаған жылуды қабылдайтын құрылғы (орган), холодильник, суықтатқыш. Ол газды белгіленген, тұрақтанған бір тӛменгі температураға 𝑇2 келтіріп отырады.
a)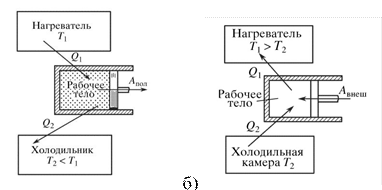 
Сурет 2. Жылу қозғалтқыштың жобасы. а-тіке бағыттағы жұмыс, б – кері бағыттағы жұмыс.
Жұмыс жасайтын дене газ немесе бу. 𝑄1 - денеге келетін жылу, барлық ӛндірілген жылу, дене қабылдаған жылу. 𝐴пол - атқарылған пайдалы жұмыс, 𝑄2 – салқындатқышқа (холодильникке) келген жылу. Суықтатқыш рӛлінде сыртқы орта - ауа да болады. Цикл аяқталғанда жұмыс жасайтын дене бұрынғы бастапқы күйіне келеді. 17-1 суретте ол 𝑃1,𝑇1 нүкте. Осы нүктеге келгенде ішкі энергия да сол бұрынғы мәніне келеді
∆𝑈 =𝑈2 −𝑈1 =0. Сондықтан келесі формула орынды
𝑄1 =𝑄2 +𝐴пол +𝑄3 +𝑄4. (1)
𝑄3 - әртүрлі жағдаймен сыртқы ортаға қайтарымсыз кеткен жылу. 𝑄4 −үйкеліс ке кеткен жылу. Жану реакциясы толық болмаған сон жоғалған, т.б. қайтарымсыз жоғалған жылулар. Жоғалған жылу әркезде болады. Яғни қабылданған, ӛндірілген жылу толығымен пайдалы жұмысқа айнамайды. Жылу энергиясын пайдаланып жұмыс жасайтын қозғалтқыштардың бұл бір ерекше қасиеті. Оның біраз бӛлігі салқындатқышқы, суықтатқышқа келеді, кіреді. (1) ден жазамыз
𝐴пол ≤𝑄1 −𝑄2. (2)
(2) жасалған пайдалы жұмыс. Теңсіздік таңба реалды, шын қозғалтқыштарға, машиналарға орынды. Теңдік таңба идеалды, жоғалған жылуы жоқ қозғалтқыштарға (машиналарға) орынды, 𝑄3 +𝑄4 =0. Пайдалы әсерлік коэффициент (п.ә.к.) тең
.
(3)
(3) тен ең идеалды деген қозғалтқыштың п.ә.к. 100% кіші болатыны шығады. Себебі 100% ке жету үшін 𝑄2 =0 болу керек. Ол мүмкін емес. Газды сығып бастапқы күйге келтіргенде суытқышқа қайтсе де бір 𝑄2 >0 жылу беріледі. 𝐴потери =𝑄3 +𝑄4 қосылғанда п.ә.к. оданда тӛмендейді.
Пайдалы жұмысты кез келген газ жасай алады.
П. 22. Термодинамиканың екінші заңы.
Термодинамиканың екінші заңын термодинамиканың екінші бастамасы деп те атайды, второе начало термодинамики. У. Томсон, М. Планк айтуы бойынша: қыздырғыштан алынған жылуды толығымен 100% пайдалы жұмысқа айналдыру мүмкін емес. Одан бұрын термодинамиканың екінші заңын келесі түрде айтқан: адиабаталық түрде изоляцияланған, тұйықталған термодинамикалық жүйеде кез келген процессте энтропия не тұрақты болады, немесе ӛседі ∆𝑆 ≥0. Термодинамиканың осы заңынан Клаузиустың және Кельвиннің шектеу принципі шығады: суық дененің ішкі энергиясын (жылуын) алып, оны температурасы одан жоғары, одан қызу денеге беріп, сол арқылы тек қана пайдалы жұмыс жасау мүлде мүмкін емес. Практикада ондай айналымды процесс болмайды. Энтропияның ӛсу заңын алдағы параграфта дәлелдейміз. Бұл жерде тек қана деген сӛз маңызды. Егерде сыртқы ортада, яғни жүйеде бұдан да тысқары басқа процесстер параллельно жүріп жатса – онда Клаузиустың шектеу принципі орындалмайды. Мысалға мұздатқыш машиналар (холодильниктер) жұмыс жасайды. Олар электр тоғының энергиясын пайдаланады. Сӛйтіп температурасы тӛмен ортадан жылуды алып температурасы одан жоғары ортаға сол жылуды береді. Электр тоғын пайдалану – сыртқы ортада ӛзгерістер болмау керек деген принципті бұзады. Клаузиустың шектеу принципі екінші типті мәңгілік қозғалтқышты жасауға болмайтынын дәлелдейді. Шынында, мысалға барлық океандағы судың температурасын 0,1 оС суыту арқылы қозғалтқыш жасаса, оның энергиясы әлемдегі барлық машинаға 1500 жылға жетер еді. Осындай қозғалтқыштарды екінші типті қозғалтқыш дейді. Бірінші типті мәңгілік қозғалтқыштардың мүмкіне еместігі олардың энергияны сақталу заңына қайшы келетіннен шығады.
Клаузиустың шектеу принципі (заңы), Томсон-Планк шектеу принципі, энтропия ӛсу заңы – термодинамиканың екінші заңының үш бірдей тең бағалы тұжырымы болады.
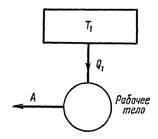
Сурет 1. Томсон-Планк шектеуі бойынша мүмкін емес
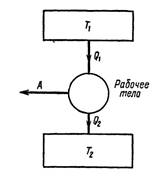
Сурет 2. Термодинамиканың екінші заңы бойынша мүмкін процесс
П. 23. Карно циклы.
Жылу қозғалтқыштардың қасиетін білу үшін, және п.ә.к. есептеу үшін Карно келесі идеалды машинаның циклын қарастырды, сурет 1.
a)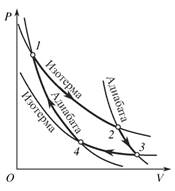 
б)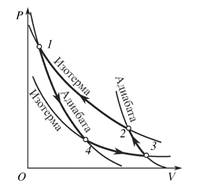 
Сурет 1. Карно циклы. а-тіке процесс, б-кері процесс.
Жұмыс жасайтын дене – идеалды газ. Мұндағы процесс идеалды. 1-2 нүктеде температура 𝑇1, дене қыздырғышпен тығыз контактіде болады. Бұл изотерма, газ кӛлемі ӛседі. 2-3 адиабата, газ кӛлемі ӛседі. 3-4 изотерма, температура 𝑇2 . Суытқыштың температурасы, дене суытқышпен тығыз контактіде болады. 4-1 адиабата, газ бірінші бастапқы кӛлемге дейін сығылады. Сонымен қоса 17-2 суретті қарау керек. Ол тіке бағытта жұмыс жасайтын машина.
1-2 аралығындағы кӛлемді үлкейтуге кеткен жылу мӛлшері, (14-6) формуладан
.
(1)
3-4 аралығындағы бӛлінген жылу мӛлшері
.
(2)
2-3 аралығында газ кӛлемі адиаталық түрде ӛседі. 4-1 аралығында газ кӛлемі адиабаталық түрде кішірейеді. 1 – нүктеде бастапқы алғашқы күйіне келеді. Сонда жасалған жұмыс
.
(3)
П.ә.к. болады
𝑉2 𝑉3
. (4)
𝑉1
(15-5) формуладан шығады
.
(5)
(5) ті (4) ке қоямыз, сонда болады
.
(6)
(6) формула ӛте маңызды, бүкіл техникалық физикада, термодинамикада, жылу машиналаларын зерттегенде ӛте үлкен роль атқарады. Осыдан термодинамиканың екінші заңының Карно бойынша анықтамасы шығады: идеалды жылу машинаның п.ә.к. жылытқыштың температурасы 𝑇1 және салқындатқыш температурасы 𝑇2 - осы екеуімен ғана анықталады.
П. 24. Карно теоремалары.
Термодинамиканың екінші заңынан, екінші бастауынан Карноның екі теоремасы шығады.
Бірінші теорема. Идеалды Карно циклының п.ә.к. жұмыс жасайтын дененің түрінен, затынан тәуелді емес, байланысты емес.
а)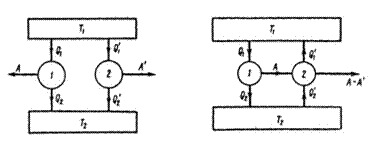 
б)
Сурет 1. Тіке а) және кері б) бағытта жұмыс жасайтын қоосарланған екі жылу машинасы.
Тағы да 17-2, 20-1 суреттерді қарастырайық. Бірінші машинанаың п.ә.к. 𝜂1 ол 17-2 суретке сәйкес тіке бағытта жұмыс жасайды. Екінші машинанаың п.ә.к. 𝜂2 ол 20-1 суретке сәйкес кері бағытта жұмыс жасайды. 𝜂1 >𝜂2 - деп есептейік. Мысалға бірінші машинадағы газ идеалды болсын, ал екінші машинадағы газ идеалды емес, реалды болсын. Содан п.ә.к. айырмашылығы туындайды.
Бірінші машинаның п.ә.к. 
. Екінші
машинаның п.ә.к.
.
𝑄1′ =𝑄1 (1)
жағдайға келтірейік. Оны
машыналардың жұмыс жасаған циклын ӛзгертіп отырып
істеуге болады. Сол кезде машиналар бірдей жұмыс жасаған болса 𝐴=𝐴′
- онда термодинамиканың бірінші заңынан 
шағады. Осыдан 𝜂1 =𝜂2
шығады. Ал біздің болжам бойынша 𝜂1
>𝜂2 . Яғни
𝐴>𝐴′
және 
. (2)
Екінші машина салқындатқышқа кӛбірек жылу береді. Бұл пайдаланбай қалған жылу мӛлшері. Екінші машина салқытдатқышқа кӛбірек жылу береді.
Екінші машинаны кері бағытта жұмыс жасайды. Сол кезде
қыздырғышта ӛзгеріс болмайды, себебі (1) орынды. (2) ден шығады
.
(3)
Қорытынды жасалған жұмыс болады
𝐴результат =𝐴−𝐴′ >0. (4)
(1)-(4) кӛрсетеді: қыздырғышта ӛзгеріс жоқ. Яғни қыздырғыш ешқандай жылуды жоғалтқан жоқ, машиналарға берген жоқ. Салқындатқыш (суытқыш) (3) мӛлшерде ӛзінің жялуын жоғалтты, екі машинаға берді. Нәтижесінде пайдалы жұмыс (4) орындалды. Яғни температурасы тӛмен денеден жылу алынып, тек қана бір денеден жылу алынып нәтижесінде пайдалы жұмыс жасалды. Сыртқы (внешний) ортада ӛзгеріс болмады. Томсон-Планк және Клаузиус-Кельвин шектеулері бойынша бұл мүмкін емес. Сондықтан екі машинаның п.ә.к. 𝜂1 >𝜂2 әртүрлі деген біздің алғашқы болжауымыз қате, орынсыз. Яғни 𝜂1 =𝜂2 болуы қажет. Сӛйтіп Карно бірінші теоремасы дәлелденді. Машиналарды бір бірімен орын ауыстырғаннан ештеңе ӛзгермейді, дәлелдеу жолы осындай болып қалады.
Карноның екінші теоремасы: Карноның идеалды циклы ең жоғарғы п.ә.к. ие болады. Басқа қайтарымсыз циклдармен салыстырғанда. 𝜂𝐾 > 𝜂р, р-реалды процесстің циклы деген сӛз.
Бұл жерде реалды деген сӛзде екі еселік мағна жатыр: 1) реалды газ жұмыс жасайды, 2) сыртқы ортаға жылу кетеді, үйкеліске жылу кетеді, сӛйтіп процесс адиабаталық емес болады.
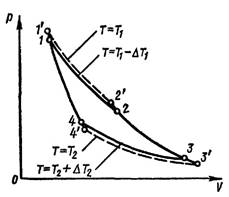
Сурет 2. Реалды Карно циклы. Штрих – идеалды жағдай.
Жоғарыда идеалды циклды
қарастырғанда жұмыс жасайтын газ (дене) әуелі, цикл
басталарда 𝑇1
, ал цикл аяқталғанда 𝑇2
температураны дәлме дәл ие болады. Қыздырғышпен
және суытқышпен жылу контакт тығыз, идеальный болады. Идеалды
емес, реалды жағдайда ол температураларға дене жетпеуі
мүмкін. Жоғарғы мәні 𝑇1
−∆𝑇1 болады, ал ең
тӛменгі мәні 
болады, сурет 20-2. Яғни
жоғарыдан қыздыру жетпей тұрады, ал тӛменнен суыту
жетпей тұрады. 1’-2’-3’-4’ – қайтарымды идеалды процесс, 1-2-3-4 –
қайтарымсыз реалды процесс. Сонда
.
. (5)
.
(6)
Қайтарымсыз (реалды) Карно термиялық циклының п.ә.к. қайтарымды
(идеалды) Карно термиялық циклының п.ә.к. нен артық, үлкен болады.
, 
болады.
Сондықтан
.
П. 25. Клаузиус теоремасы.
Идеалды машинаның п.ә.к.
(1)
келесі түрде жазамыз
.
(2)
Берілген не қабылданған жылу мӛлшерінің температураға қатынасын келтірілген (приведенное) жылу мӛлшері дейді. Идеалды Карно циклында изотермиялық кеңею мен сығылу процесстерінің келтірілген жыжулары бірдей болады.
1-суретте (1anb1) бірқалыпты циклдық процессті қарастырайық.
Кӛптеген қатар, қатар
орналасқан Карно процесстеріне бӛлейік. Олар параллельно
сызылған адиабаталардан, және изотермалардан тұрады.
Әрбір кішкентай циклде машина кішкентай мӛлшерде жылуды алады,
және кішкентай мӛлшерде жылуды береді. 
- әрбір
кішкентай циклдағы қыздырғыштағы температуралар,
ӛзеріс сатылы, ступенчато. 
- әрбір кішкентай циклдағы
суытқыштағы температуралар, ӛзгеріс сатылы, ступенчато. 
–
әрбір кішкентай циклдегі қыздырғыштан денеге
қабылданған жылу, a – сызығының бойында.
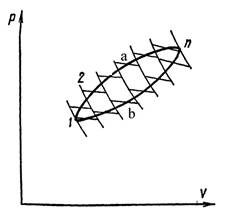
Сурет 1. Тұйықталған циклды кӛптеген
идеалды Карно циклдарымен жуықтау.
- әрбір кішкентай циклдегі жұмыс
жасаған газдан
суықтатқышқа (холодильникке) келген жылу, b – сызығының бойында. Әрбір жекеленген кішкентай Карно циклы параллельді екі адиабата және екі изотерма арасында орналасқан. (2) формуланы әрбір жекеленген, индивидуальный Карно циклына жазамыз
; ··· ; 
.
(3)
(3) -тегі барлығын қосқанда болады
.
(4)
Келтірілген жылу мӛлшерінің қосындысы процесстің жүрген жолына байланысты емес. 1an = nb1. Осы маңызды нәтиже Клаузиус теоремасы деп аталады.
Идеалды емес, қайтарымды емес, қайтарымсыз реалды процессте болады п.ә.к.
.
(5)
Бұл жерде қайтарымсыз деген сӛзде сыртқы ортаға қайтарымсыз жылу жоғалу бар дегені. Келесі түрде жазамыз
.
(6)
Тең болады егер процесс бірқалыпты қайтарымды болса. (6) келесі түрде жазамыз
.
(7)
таңбасы плюс
(+) болады, ол жұмыс жасайтын денеге келіп жатыр, 
таңбасы
минус (-) болады, ол жұмыс жасайтын денеден кетіп жатыр. Яғни біз
денеге (газды ортаға) байланысты қарастырамыз деген сӛз,
система отсчета связана с рабочим телом. Сонда (7) болады
.
(8)
(8) ді 1 суреттегі барлық n-1 циклге жазғанда болады
.
(9)
Қосындының саны кӛбейгенде, шекті жағдайда қосынды интегралға айналады. Бұл математикалық талдау (математический анализ) курсынан белгілі. Сонда (9) дан болады
.
(10)
(10) Клаузиустың интегралдық теңсіздігі. Тұйықталған термодинамикалық процессте келтірілген жылу мӛлшерінің интегралы: 1) нольден кіші – егер процесс қайтарымсыз, реалды болса, 2) нольге тең егер процесс қайтарымды, идеалды болса. Онда сыртқы ортаға пайдасыз жылу жағалуы болмайды.
П. 26. Энтропия.
23-1 суреттегі 1anb1 тұйықталған циклды қарастырайық
=
0. (1) Циклдағы процесс
қайтарымды, идеалды болсын. Яғни пайдасыз жылу жоғалу
жоқ. Интегралда қисық сызықты интерал сияқты кері
жаққа интегралданады. Сондықтан
.
(2)
(2) кӛрсеткендей интегралдың нәтижесі жолдан тәуелді емес. Осыдан (2) әлдебір функцияның толық дифференциалы болатыны шығады. Осы функцияны Клаузиус энтропия деп атады. S деп белгіленді. Энтропос – грек сӛзі, бұрылыс, айналып қайтып келу деген мағнада. Сондықтан болады
.
(3)
Ӛлшем бірлігі Дж/град. Дененің әрбір күйі энтропияның белгілі бір мәнімен сипатталады. Ішкі энергия U сияқты. Энтропия S-де ішкі энергия U сияқты толық дифференциалы бар функция. (3) формуламен тек қана энтропия айырмашылығы ғана еспетеледі. Энтропияның абсолюттік мәнін есептеу үшін оның бір нүктедегі мәні белгілі болу керек. Содан кейін ғана ӛзгеріс, ӛсімшені (3) формуламен есептейді. Содан абсолюттік мән шығады.
Жылу беретін жүйенің температурасы (𝑇1) тӛмендеу болса п.ә.к.-де тӛмендеу болады, ал керісінше энтропия S жоғары үлкендеу болады. Ӛйткені температура бӛлімінде тұр. Энтропияның ӛсуі п.ә.к. тӛмендеуіне келтіреді. Сондықтан энтропияны дененің энергиясының құнсыздануының мӛлшері деп түсінеміз.
Келесі дифференциалдық функция бар екенін
(4)
(25-10) да шығаруға болады. Тек онда идеалды циклды қарастыру керек. Энтропияның “ерекше”, “қызық” функция екенін (25-10)-нан кӛруге болады.
Идеалды толық айналымды, тұйықталған (бастапқы нүктеге қайтып келген, замкнутый) циклде
𝑑𝑆 =0, ∆𝑆 =0, 𝑆𝑘 =𝑆2 =𝑆1
болуы мүмкін. Идеалды емес, яғни қайтарымсыз, жылу жоғалуы бар кездері, сондай толық айналымды, тұйықталған циклде әрдайым
∆𝑆 >0, 𝑆𝑘 =𝑆2 >𝑆1. (5)
(5) ті реалды процесстерде, қайтарымсыз жылу жоғалу барда энтропияның ӛсіп отыруы – деген фундаменталды, іргелі заңы деп атайды. Физиктер осыдан “Теория тепловой смерти вселенной” деген де тұжырым жасаған. Қайтарымсыз жылу жоғалу бар кезде толық айналымды, тұйықталған жолдағы энтропия ӛзгерісі ∆𝑆 ≠0.
П. 27. Қайтарымсыз процесстегі энтропия ӛзгерісі.
25-1 суретті қарастырайық. Сонда 1an бӛлігі қайтарымсыз болсын. Ол бірқалыпты емес процесс. Екінші nб1 бӛлігі қайтарымды, бірқалыпты болсын. (25-10) ды келесі түрде жазамыз
.
(1)
(1) ді келесі түрде жазамыз
.
(2)
(2) формула кӛрсеткендей қайтарымсыз жолдағы интеграл қайтарымды жолдағы интегралдан кӛп, артық болады.
Сонымен қоса қайтарымды жолдағы интеграл энтропия ӛзгерісіне тең
.
(3)
(2) мен (3) тен шығады
.
(4)
Яғни (2)-(4) тен шығады
.
(5)
Қайтарымсыз жолдағы интеграл энтропия ӛзгерісінен кіші болады. Немесе қайтарымды жолда энтропия ӛзгерісі максималды болады. Қайтарымды бірқалыпты циклдарда (бұл идеалды процессте ғана
болады)
.
(6)
Тұйықталған контурдағы
интеграл, қайтарымды тұйықталған жолдағы
интеграл, энтропия ӛзгерісі нольге тең болады 
. Ӛте
аз ӛзгерістерге дифференциалды түрде жазамыз
.
(7)
Бұл жерде қайтарымсыз – ол сыртқы
ортаға кеткен, яғни қайтып келмейтін жылу жоғалуы бар
процесстер. Ал қайтарымды процесс, барлық жылу тек пайдалы
жұмыс жасауға жұмсалды, бос кеткен жылу жоқ, яғни
идеалды Карно циклына сәйкес деген мағынада. Қайтарымды,
идеалды процессте энтропия потенциалды функция ретінде бар болады, оның
толық дифференциалы болады. Ал реалды циклдарда – оны: не
анықталмаған функция, немесе ерекшелігі бар, қызық
функция деп қарастыру керек, яғни потенциалды емес, не однозначная,
а многозначная функция своих аргументов: P и V. Толық дифференциалды емес
функция болады. Ӛйткені, кәдімгі математикалық
тұрғыдан анықталатын потенциалды функциялардың
барлығының тұйықталған қисық
сызық бойынша жазықтағы интегралдары әрдайым 
болып
отыруы қажет. Қайтарымсыз (жылу жоғалуы бар) процесстерде
тұйықталған контурда 
болатыны шынымен
қызықты физикалық факт. Л. Больцман S энтропиямен макро
системаның күйінің статистикалық
ықтималдығын W келесі формуламен байланыстырды
.
(8)
Мұнда k – Больцман тұрақтысы, W – макрожүйенің (мысалға бір үлкен ыдыстағы газдар молекуласы) күйінің ықтималдығы. Макрожүйенің ең ықтималдығы жоғары күй – ол барлық молекулалардың температура бойынша, кинетикалық энергия бойынша теңескен, бірқалыпты (равновесное состояние) күй болады.Ең тӛмен салқындаған күй. Осыдан 19 ғасырдағы физиктер ғарыш (космос) әлемінің жылулық энергия бойынша теңескен, яғни жылулық бойынша “ӛлген” кезі болады деген. Теория тепловой смерти вселенной. Контур бойынша интегралдарды, толық дифференциалды жақсы түсіну үшін қосымша қараңыздар: Фихтенгольц Г. М. Дифференциальное и интегральное исчисления. – Том 2. – М.: Наука, 1970. – 800 с. ; Пискунов Н. С. Дифференциальное и интегральное исчисления. – Том 2 – М.: Наука, 1972. – 576 с. ; Толстов Г.
П. Элементы математического анализа. – Том 2.- М.: Наука, 1966. – 462 с.
Тарау 2. Термодинамикалық потенциалдар теориясы. Физикалық химия негіздері.
П. 1. Термодинамиканың бірінші, екінші заңдары.
Біріккен термодинамиканың заңы.
Термодинамиканың бірінші және екінші заңдары бойынша
,
(1) 
.
Қабылданған жылу мӛлшері dQ екі нәрсеге жұмсалады: 1-ішкі энергияны ӛсіреді dU, 2 – жасалған жұмысқа жұмсалады dA.
Осы (1) ден болады
.
(2)
,
,
(3)
.
(3) теңдеулер – термодинамиканың бірінші және екінші заңдарының біріккен түрі деп аталады. Осы теңдеулердің әр қайсысы 5 маңызды термодикалық функцияларды (P,V,T,S,U) бір бірімен байланыстырады. Әрбір теңдеуде екі шаманы тәуелсіз, еркін, дербес, независимая айнымалы деп қабылдайды, сонда қалған үшеуі – анықталатын функция.
П. 2. Ішкі энергия және оның дербес туындылары.
Тәуелсіз айнымалы деп V мен S ті алайық. Сонда анықталатын функция ішкі энергия U болады. Оның толық дифференциалы
(1)
(1-3) [параграф 1, формула (3) деген белгі] – тен және (1)-ден шығады
,
(2)
p
.
(3)
Яғни (1)-(3) тегі белгісіз функциялар (p,T) маңызды функцияның U дың S және V арқылы дербес туындылары арқылы анықталады.
(2), (3) тің екінші туындысын алайық
,
(4)
- кез келген
мольдың жылу сыйымдылыңы, Дж/K. Мұнда келесі формулалар
ескерілді
,
(5)
,
(6)
,
(7)
мұнда 
индексі 1
мольға арналған, 1 мольдік екенін кӛрсетеді. Кӛп
жағдайда оны жазбайды. Осыдан
.
(8)
(8) – қызықты және маңызды формула.
(2) – ні V бойынша, (3) – ті S бойынша туындылайық. Сонда болады
,
(9)
.
(9) дан шығады
. (10)
(10) термикалық және калориметрикалық параметрлерді байланыстырады.
П. 3. Энтальпия және оның туындылары
Тәуелсіз екі айнымалы p мен S болсын.
Сондағы термодинамикалық функцияны H деп белгілейік, 
. Осы функцияның
толық
дифференциалын табайық
. (1)
(1-3) формуланы түрлендірейік. Екі жағынан Vdp қосамыз
.
Немесе
.
Немесе
.
(2)
(2) ден
(3)
функциясы бар екен деп айта аламыз. Оны энтальпия деп атайды, кейбір кітаптарда I –деп белгілейді. Сонымен (1-3) тен шығады
.
(4)
Және де
,
(5)
.
(6) (1–1) ден болады
.
(7)
(7) ден
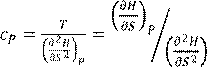. (8)
(5)- ті p, (6)-ны S бойынша туындылайық
.
(9)
(9) дан болады
.
(10)
Немесе, кері туынды (производная обратной функции) ережесі бойынша
.
(11)
Сондықтан энтальпия функциясының 
бірінші
туындысы термикалық параметрлерді анықтайды, ал екінші ретті
туындысы арқылы калориметрикалық 
функция
анықталады. Сонымен қоса
,
(12)
- 1 моль заттың жылу
сыйымдылығы.
П. 4. Гельмгольц функциясы. Изохорлы-изотермиялық потенциал.
Гельмголь функциясы жүйедегі жалпы энергияны сипаттайды, содан оны Гельмгольцтың энергиялық функциясы деп те атайды. Бұл жолы ерікті, тәуелсіз екі айнымалы ретінде V мен T қарастылылады. (1 – 3) тен келесіні аламыз
.
(1)
Осының екі жағынанан SdT аламыз:
.
(2)
(2) нің сол жағы бір функцияның толық диффренциалын білдіреді
.
(3)
Осы F –функцияны Гельмгольц функциясы деп атайды
.
(4)
(4) тің толық дифференциалын F тің дербес туындылары арқылы жазайық
. (5)
(1), (2), (5) тен шығады
,
(6)
.
(7)
(7) нің екінші туындысын алғанда, изохорлық жылу сыйымдылықты табуға болады
.
(8)
(8) ді түсіну үшін (2-5) ті қараңыздар. Осыдан
.
(9)
(6), (7) ден екінші туындыны алайық
.
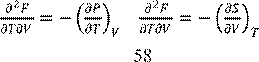(10)
Осыдан
.
(11)
(11) ден кері функциялар заңдылыған шығады
.
(12)
(9)-(12) термодинамикалық функциялар теориясында маңызды.
(3) формулада 
– сыртқы
күштерге қарсы жұмыс деп жазамыз. Системаның ішкі
қысымының ӛз кӛлемін ұлғайта отырып,
сыртқы күштерді итере отырып, атқарылған жұмыс.
Сонда
.
(13)
Изотермиялық процессте Т=const болады
.
(14)
Изохорлы және изотермиялық жағдайды қарастырайық V=const, T=const
Сонда қысым жұмыс жасамайды 
.
Және ішкі энергия 
ӛзгермейді. Бірақта, сол
кезде де 
функция ӛзгереді. Сол
ӛзгерісті механикалық емес күштердің жасаған
жұмысы деп түсінеміз
.
(15)
Мысалға электромагниттік күштердің, индукциялық тоқтардың жасаған жұмысы деп түсінуге болады. Cонымен толық жұмысты былай жазуға болады
.
(16)
Яғни Гельмгольц функциясының ӛзгерісі толық жұмысты қамтиды: ішкі және сыртқы. F – ішкі энергия, связанная, байланысқан энергрия деп атайды. Оның ӛзгерісі екі жұмыс түріне жұмсалады: 1 – кәдімгі жұмыс
, 2- механикалық
емес жұмыс түрі - 
. Осы жұмыс жылуға айналуы
мүмкін. Сондықтан оны изохорлы-изотермиялық потенциал деп
атайды.
П. 5. Гиббс энергиясы. Изобарлық-изотермиялық потенциал.
Термодинамиканың бірінші заңын келесі түрде жазамыз
.
(1)
Екі жақтан да 
) ӛрнегін
қосамыз
.
(2)
Сол жақтағы ӛрнекті толық диффренциал ретінде жазамыз
.
(3)
(3) тің сол жағынан келесі функция бар екені шығады
.
(4)
(4) – Гиббс функциясы. Оның екі тәуелсіз айнымалысы бар: p,T. Сондықтан оны изобарлы-изотермалы потенциал деп атайды.
.
(5)
функцияның
толық дифференциалын қарастырайық
.
(6)
(5), (6) дан шығады
, (7)
. (8)
(7), (8) маңызды функцияларды Гиббс потенциалының дербес туындылары арқылы анықтап береді. (7) ні T бойынша (8) ді Р бойынша туындылайық
,
(9)
.
(10)
(9) бен (10) нан шығады
.
(11)
Келесі формулаларды еске түсірейік
.
(12)
(12) ден және (8) ден шығады
.
(13)
(13) маңызды формула, қысым тұрақты болғандағы жылу сыйымдылықты анықтайды.
П. 6. Термодинамикалық потенциалдар және
механикалық емес жұмыс.
Әртүрлі параметрлер
тұрақты болғанда, системада әртүрлі пайдалы
жұмыс жасалады. Оны 
деп белгілейміз. 
.
Яғни қысым күшінің жұмысы мүлде болмағанда да атқарылатын жұмыстардың басқа түрі болады. Сонда жалпы жұмыс тең
.
(1)
Сонда термодинамиканың екінші заңы келесі түрде жазылады
. (2)
Тәуелсіз, дербес екі айнымалы ретінде S, V болсын. Сонда (2) былай жазылады
,
немесе
.
(3)
S=const, V=const болғанда 
яғни
ішкі энергия 
термодинамикалық потенциал
болады.
Тәуелсіз, дербес екі айнымалы ретінде S, P болсын.
Сонда (2) былай жазылады
Немесе (3-3) формуланы ескере отырып, интегралдаған сон
.
(4)
S=const, P=const болғанда 
яғни
энтальпия 
термодинамикалық потенциал
болады.
Тәуелсіз, дербес екі айнымалы ретінде T, V болсын.
Сонда (2) былай жазылады
.
Осыдан
.
(5)
(5) тен болады
.
(6)
(п.4-4) формула бойынша (6) ны былай деп жазамыз, интеградаған сон
.
(7)
Яғни қайтып келмелі (обратимый) изохорлы-изотермалы процессте Гельмгольц функциясының ӛзгерісі механикалық емес жұмыстың максималды мәніне тең.
Тәуелсіз екі айнымалы ретінде p мен T болсын. Сонда
.
(8)
(8) ді былай жазамыз
.
(9)
(9) -ды (5–4) арқылы жазамыз
.
(10)
(10) ды интегралдағанда болады
−∆𝐺 =𝐴′𝑚𝑎𝑥 ,𝑃 . (11)
Қайтармалы (обратимый) изобарлық-изотермалық процессте Гиббс функциясының ӛзгерісі механикалық емес жұмыстың максималды мәніне тең болады.
Изотермалық процессте (4-3) тен шығады
. (12)
,
Мұнда 𝜇 таңбасы 1 мольге қатысты шамалар екенін кӛрсетеді, кейінде ол таңбаны жазбаймыз.
(5-5) тен шығады
.
(13)
(12), (13) тегі формулалар 1 кмоль газға қатысты жазылған. Енді
𝑃𝑉𝜇 =𝑅𝑇 (14)
формуланы пайдаланамыз. (12)-(14) тен шығады
.
(15)
Ал (13)-(14) тен шығады
.
(16)
(15) пен (16) кӛрсеткендей изотермалық процессте
∆𝐺 =∆𝐹, 𝐴′𝑚𝑎𝑥 ,𝑃 =𝐴′𝑚𝑎𝑥 ,𝑉 . (17)
П. 7. Гиббс-Гельмгольц теңдеуі.
(4 - 4) және (5-4) қарастырайық. Сондағы S-ті (4-7) және (5-8) формулалары арқылы ӛрнектейміз. Содан келесі формула шығады
,
(1)
.
(2)
(1) ші теңдеуде V, T тұрақты, (2)
ші теңдеуде P, T тұрақты. Осы екі формулада 
және 
ӛзгерістері
сол ӛздерінің температура арқылы туындысымен
ӛрнектеледі, байланысады. Осы екі формуланы (1), (2) – Гиббс – Гельмгольц
теңдеулері деп атайды. Енді келесі формулаларды пайдаланайық
. (3)
(1)-(3) тен шығады
, (4)
Термодинамикалық функциялар бойынша негізгі нәтижелерді жинақтап келесі кестеге түсіреміз
Кесте 1
|
Айным алылар атауы |
Сипаттаушы функциялар |
Жұмыстың формуласы |
функциялардың дербес туындылары |
Дербес туындылар арасындағы байланыс |
||
|
V,S |
Ішкі энер гия U |
|
p
|
|
||
|
P,S |
Энтальпия
|
|
|
|
||
|
|
|
|
|
|
||
|
T,V |
Энергия Гельмголь ца,изохорноизотермичес кий потен циал F=U-TS |
|
|
|
||
|
P,T |
Энергия Гиббса,изо барно-изо термическ ий потенц иал G=H-TS |
|
|
|
,
|
|
|
|
||||||
, 
, 
. 
. 
, 
П. 8. Химиялық потенциал
Жоғарыда айтылған термодинамика функциясының ғылымында (теориясында) жүйенің массасы тұрақты болды. Осы параграфта жүйенің массасы ӛзгеретін жағдайды қарастырамыз. Мысалға химиялық реакциялар жүреді, жылжымалы шекарадан диффузия болады, конвективті масса ағыны болады, т.б. Осындай кезде термодинамикалық жүйені сипаттауға бұрынғыдай екеу емес, үш дербес айнымалы керек: екеуі термодинамикалық функциядан болса, үшінішісі – бар заттың киломольын (заттық мӛлшерін) кӛрсететін, сипаттайтын шама – жаңа айнымалы болады. Сонда: ішкі энергия
 |
,
(1)
энтальпия
,
(2)
Гельмгольц функциясы
,
(3)
Гиббс функциясы
(4)
деп жаза аламыз. Мұнда 
–
қоспаның ішіндегі әртүрлі заттардың
киломольдық шамалық, сандық кӛрсеткіші. Сонда (3)
тің толық дифференциалын келесі түрде жазамыз
+…
. (5)
Киломольдық, зат мӛлшерінің
айнымалылары 
бойынша дербес туындыларды Гиббс (1875
ж.) химиялық потенциал деп атады. Бастапқыда Гиббс 
ны зат
мӛлшері киломоль емес, массалық (кг) бірлікпен ӛлшеген еді.
Гиббс функциясының бір компонентаның
мольдық мӛлшерінің ӛзгерісі (
) бойынша
алынған туындысы сол компонента бойынша анықталған
химиялық потенциал деп аталады. Сол кезде басқа
компоненталардың мольдарының саны және P, T -
тұрақты болу керек. Айтқанымыз формула бойынша
ӛрнектеледі
,
,
,
, 
. . . . . . . (6)
.
Сонда, әрбір химиялық потенциалдың ӛзінің айнымалысының дифференциалына кӛбейтіндісі тең болады Гиббс функциясының диффернциалына, бірақ толық емес, тек P=const, T = const болғандағы.
(7)
Ал Гиббс функциясының толық ӛзгерісі тең болады
.
(8)
Мұнда 
. (9)
,
Немесе
, (10)
.
(11)
(6) жүйеде екі тәуелсіз айнымалы 
тұрақты.
Сол сияқты V,S тұрақты болғанда 
iшкі
энергия U дың дербес туындысы арқылы анықталады. P,S
тұрақты болғанда 
энтальпия H тың дербес туындысы
арқылы анықталады, V, T тұрақты болғанда 
Гиббс
функциясының дербес туындысы арқылы анықталады. Формула
ретінде жазамыз
,
, 
(12)
.
,
(12) ні
қорыта айтқанда химиялық потенциал 
тӛрт функция
арқылы бірдей анықтала алады – (U,H,F,G), 
.
Кӛп жағдайда парциалдық бір киломольдық мәні арқылы жазылады
,
- бір киломольдық Гиббс энергиясы
деген сӛз.
Химиялық потенциалдың физикалық мазмұнын анықтайық. Сол үшін келесі формуланы қарастырамыз
.
(13)
(13) формула (6-2) ден шығады. Сонымен қоса
.
(14)
- механикалық емес жұмыстан
басқа барлық жұмыс түрі, мысалға электрлік
күштердің жұмыс болуы мүмүкін.
(13), (14) тен шығады
.
(15)
(15) кӛрсеткендей, химиялық потенциалдың сол заттың мольдық кӛлемінің ӛзгерісіне кӛбейтіндісі белгілі бір механикалық емес жұмысқа тең болады. Механикалық емес жұмыс дегеніміз мысалға электр ӛрісінде заряд ӛзгерісі жұмыс болуы мүмкін
.
(16)
(15), (16) кӛрсеткендей 
- моль саны
, 
– заряд молшері. Осылар экстенсивті шама,
яғни заттың мӛлшері, зарядтың мӛлшері, натуралды
немесе рационалды санмен сипатталады. Мысалға 1,2,3, ...
n.
- химиялық потенциал, 
-
электр ӛрісінің кернеулігі. Бұлар интенсивті шамалар.
Мысалға заттың массалық тығыздығы 
– ол да
интенсивті шама. Яғни интенсивті шама бір шаманың екінші
шамаға қатынасымен сипатталыды, жалпы бір заттың екінші
затқа байланысты тығыздығы. Яғни тығыздық
деген ұғым тек қана массаға ғана байланыс- ты
емес ұғым.
Яғни 
-
химиялық жұмыстың потенциалы болып табылады.
Әртүрлі химиялық потенциалы бар жүйе бір бірімен
қосылғанда, араласқанда әртүрлі потенциалдар 
біртіндеп
теңеседі, бірдей мәнге келеді. Теңесу 
-зат
мӛлшерінің ӛзгерісіне байланысты түрде болады.
Сондықтан химиялық потенциал 
химиялық
ӛзгерістермен жүріп жататын процесстердің
қозғалтқыш күші деп түсінеміз. Фазалық,
массалық, күйлік ӛзгерістермен сипатталатын процесстерді
айтамыз.
П. 9. Тепе-теңдік күйдегі жүйе. Гиббс-Дюамель теңдеуі.
Барлық потенциалдар теңесіп бір мәнге келгенде – тепе теңдік күйге келдік деп атаймыз. Химиялық, заттық ӛзгерістер бойынша.
Жалпы айтқанда химиялық потенциалды келесі формуламен сипаттаймыз
.
(1) Идеалды бір газ немесе газ қоспасын стандартты қалыпты
(ӛзгеріссіз)
теңескен жағдайда
қарастырайық, 
, 
. (п.8-11), (п.8-12)
кӛрсеткендей 1 мольге деп қарастырғанда сонда болады
=
const. (2)
Осындай қалыпты күйде тұрған идеалды газдардың қоспасына болады
.
(3)
(3)-ны дифференциалдағанда болады
.
(4)
(4)-ны (п. 8-11)-ге теңестірейік
. (5)
(5) ден шығады
. (6)
(6) ны Гиббс-Дюгема теңдеуі деп атайды.
(3) теңдеудің ерекшелігі. Ол тепе-теңдік күйдегі жағдайды сипаттайды. Яғни одан кейінгі (4)-(6) дағы ӛзгерістер бастапқы жағдай, бастапқы шарт (3) болғанда ғана орындалады деген сӛз. Начальные условия этих уравнений дейді. Яғни әртүрлі физикалық, химиялық процесстерді сипаттағанда олардың бастапқы шарты, бастапқы күйі ӛте маңызды болып табылады. Гиббс-Дюгема теңдеуі соны кӛрсетеді.
, 
болғанда (6)
дан шығады
.
(7)
П. 10. Термодинамикалық потенциалдың қысым мен
температураға байланысы.
Гиббс функциясын T және P арқылы ӛрнектейік. Сол үшін (п.5-4) формуласын пайдаланамыз. Және (п.3-11) ді пайдаланамыз. Сонда болады
.
(1)
(1 –3) тен шығады
.
(2)
Күй теңдеуін қарастырамыз
.
(3)
(3) ті дифференциалдаймыз
.
(4)
(3) ті пайдалана отырып (4) тен болады
.
(5)
Енді (5) ті (2) ге қойғанда болады
.
(6)
(6)-ны интегралдағанда болады
.
(7)
Мұнда (о) таңба – стандарттық
жағдайда деген белгі, 
, 
= 293 K. Яғни
интегралдау стандарттық жағдайдан (о) кез келген
жағдайға дейін жасалады (P,V,T). Қысым үшін
атмосфералық бірлік қабылдаймыз. Енді (5-4), (10-1)
формулаларды пайдаланамыз. Сонда болады
Интегралдағанда шығады
. (9)
Енді R=
екенін ескереміз. Сонда (9) ден болады
.
(10)
Тек қана температураға байланысты мүшелерді қосымша функция
ретінде белгілейміз
.
(11)
(10) барда (9) былай жазылады
. (12)
(11) формула физикалық химия, термодинамика, статистикалық физика курстарында аса маңызды болып табылады. Қайталап айтамыз мұнда (о) деген таңба стандартты жағдайға байланысты. Осыны абсолюттік ноль температура кезіндегі жағдай деп шатастырмауды сұраймыз.
–
Гиббс
функциясының стандартты қалыпты жағдайдағы мәні.
(9) формуланың келесі ерекшеліктері бар. 
-
Cи бірлік жүйесінде болғанымен, 
- атм бірлігінде
жазылады, ӛлшенеді. Сонда осы формула физиканың барлық
ӛлшемдер бір жүйеде, бір системада болу керек деген принципін,
заңын бұзбайды ма? – деген сұрақ туындайды. Жоқ
бұзбайды. (9)–дәл солай айтқанда, 
– атм бірлігінде
болғандағы түрі. Ал егер біз 
–ды
бұрынғыдай, үйреншікті Си
жүйесінде жазсақ (9) келесі түрде жазылады
. (13)
Мұнда 
Па.
Осыны (6), (7) формулалардан анық кӛруге болады.
(1) ші формуладағы интегралды стандарттық
жағдаға (
) және абсолюттік
температураға 
байланысты жазып, содан (9) ды одан
әрі түрлендіруге болады ма? - деген сұрақ туындайды.
Одан әрі түрленбейді, пайдасы болмайды. Cебебі
формулада 
функциясының
түрі белгісіз. Және де шеткі 
нүктеде (және
соған жақын жерлерде) 
анықталмаған, белгісіз.
Сондықтан интегралданбайды.
Кейбір әдебиетте 
деп белгіленген.
Қоспа бірнеше құрамды газдан болғанда жеке компонентаға (12) арналған формуланы жазамыз
.
(14) Мұнда
.
(15)
(9-2) бойынша
.
(16)
Мұнда (15) бойынша
. (17)
(17) ны кейде былай деп белгілейді
.
(18)
(15)-(17) газ мӛлшері 1 моль болғанда, және P, T – тұрақты болған кезде ғана орынды. Осы шарттардың біреуі орындалмаса (9 -2) де орындалмайды.
Қысымның орнына концентрация еңгізуге болады. Сол үшін газдың күй теңдеуін келесі түрде аламыз
.
(19)
Осыдан
.
(20)
Мұнда
-
(21)
киломольдық – кӛлемдік концентарция. (19)-(21) ді (16) ға қоямыз, сонда
.
(22)
(22) ға жаңа белгілеу еңгіземіз
.
(23)
Мұнда
.
(24)
(24) - жаңа константа. Химиялық потенциалдың концентрация арқылы ӛрнектелгендегі жаңа түрін кӛрсетеді.
Парциалдық қысымды газды қоспаның жалпы қысымы арқылы
ӛрнектеуге болады
.
Реалды газдар үшін қысымның орнына фугитивность еңгізеді
,
(25)
– фугитивность коэффициенті. Идеалды газ
үшін 
. Сонда 
.
(25) ді (14) ке қойғанда болады
.
(26)
Мұнда
,
(27)
,
.
(27) – фугитивность арқылы жазғандағы Гиббс функциясының жаңа интегралдау константасы. Екінші жағынан температураға ғана байланысты жаңа функция деп те оны атайды.
Газдың қысымы идеалды газ қысымынан аз ғана айырмашылығы болғанда коэффициент 𝑚𝑖 <1
.
(28)
𝑃𝑖𝑖𝑑 -идеалды газ қысымы, 𝑃𝑖 - идеалды емес, реалды газ қысымы. 𝑃𝑖𝑖𝑑 - (10-3) пен анықталады. Фугитивность үшін де газдың стационарлы, нормальды жағдайдағы деген ұғым қолданады. Фугитивность ӛлшем бірлігі – қысым. Сондық стангдартты жағдайда атм ӛлшегенде 𝑓𝑖0 =1 атм. (26) газдың идеалды еместігі азғантай болғанда орынды, яғни почти идеалды газ.
Сонда фугитивтілік коэффициенті болады
.
(29)
(28) бен салыстырсақ 𝑃𝑖 =𝑓, 𝑚𝑖 =𝛾.
П. 11. Ерітінділер термодинамикасы. Рауль заңдары.
Тұз тасы NaCl суда ериді. Бір кезде динамикалық тепе теңдік орнайды. Сонда қанша молекула тұздан суға шықса, соншама молекула судан тұзға қарай кері ауысады. Осындай күйді динамикалық тепе теңдік деп атайды, динамическое равновесие. Қаныққан ерітінді, насыщенный раствор. Температура ӛскенде еріген заттың мӛлшері аздап артады. Ерітінді концентрациясы [г/см3], [г/кг] – мен ӛлшенеді.
Сұйықтар бірі бірінде толық және толық емес еруі мүмкін. Біреуі біреуінің ішінде мүлде ерімейтіндер де болады. Мысалға сумен спирт жақсы ериді. Сумен анилин толық емес ерітеді. Бірі астыда, бірі үстіде екі қабат сұйық боп тұрады. Біреуі анилиннің судағы қаныққан ерітіндісі. Екіншісі, судың анилиндегі қаныққан ерітіндісі.
Сынап ртуть пен су бір бірінде мүлде ерімейді. Сұйықтардың бір бірінде еруі температураға байланысты. Температура ӛскенде, еру де ӛседі. Үлкен температурада қандай да болмасын сұйықтың екінші сұйықта толығымен ерітуіне болады.
Сурет 1. Сұйық-бу жүйесі.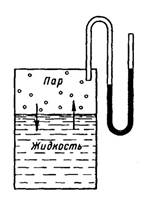
Тепе-теңдік
күй.
Сұйықтан сыртқы ортаға ауаға сұйықтың молекулалары бу болып шығады, 1 сурет. Бір кезде сұйық-бу жүйесінде тепе-теңдік күй орнайды. Сұйықтан буға шыққан молекулалар саны будан-сұйыққа кірген молекулалар санымен тең болады. Осы кездегі будың қысымын қаныққан будың қысымы деп атайды. Сол кезде ∆𝐺 =0.
Осы тепе теңдікте тұрған суға, яғни еріткішке екінші бір зат еңгізейік. Ол екінші зат судың ішінде ерітін болғанымен одан бу шықпайды. Яғни бу – тек бірінші заттыкі болып қала береді. Ерітіндінің ішінде бірінші негізгі заттың мольдық концентрациясы х1 сонымен азаяды. Соған байланысты бірінші заттың сұйық бетіндегі буының қысымы 𝑝1 азаяды, кемиді. Ӛйткені х1 азайғанда 1 ші заттың сұйық бетінен ауаға буланып ұшу қабілеті де азаяды, тӛмендейді. Сонымен 𝑝1 мен х1 арасында сызықты байланыс орындалады
𝑝1 =𝐾1𝑥1. (1)
𝐾1
коэффициентінің физикалық мазмұнын анықтайық. х1 =1 болғанда
барлық ерітінді бір ғана зат – толық ерітушіден тұрады.
Сол кезде 
. Мұнда 
– ерітінді
толығымен бір ғана заттан болғандағы соның
бетіндегі будың қаныққан қысымы. Сонда (1)
теңдеуді келесі түрде жаза аламыз
.
(2)
(2) – Раульдің бірінші заңы деп аталады. Сол бойынша ерітінді бетіндегі
заттың қысымы оның ерітінді ішіндегі мольдық (заттық) концентрациясына пропорционал болады. Пропорционалдық коэффициент ретінде сол ерітіндінің таза ӛзі болғандағы будың қаныққан қысымы болып табылады.
(2) ні басқа түрде жазамыз.
Ерітіндіге араласқан екінші заттың мольдық концентрациясы 
.
Сонда 
. Содан былай жазамыз
.
(3)
(2) ні келесі түрде жазамыз
.
(4)
(4) Раульдің 1 ші заңының екінші жазылу түрі.
Ерітіндіде екі зат болсын. Сонда екінші компонентаға арналып (2) формула келесі түрде жазылады
.
(5)
(4) ші формула келесі түрде жазылады
.
(6)
(2)-(6) формулаға сәйкес болатын заңдылықтарды идеалды ерітінді дейді. Бензол – толуол идеалды ерітіндісіндегі будағы жалпы және парциалдық қысымның концентрацияға байланысты ӛзгерісі 1, 2 – суреттерде кӛрсетілген. 2-суретте l - сызық (жидкость) және 1 ші суреттегі “общее давление” сызығы – екеуі де – бір сызық. Ол будың ерітіндімен тепе теңдік күйде тұрғандағы жалпы қысымы. Сұйықтың бетіне жақын кездегі қысым, сондықтан сұйық қысымы деп аталған. Құрамы абсциссада айтылған. v-сызық - будың критикалық күйдегі сызығы. Қысымды сәл қӛбейткенде – бу дереу конденсациялана бастайтын күйді – будың қысым бойынша критикалық күйі дейді. V- қысымы будың ортасында ӛлшенеді. Сұйық бетінен алыстау жерде. V- мен l - ді жалғап тұрған пунктирді сызық – байланыс сызығы деп аталады.
Парциалды және жалпы қысым. 1 – жалпы қысым, 2 – бензолдың парциалды қысымы, 3 –толуолдың парциалды қысымы
Сурет 2 – Бензол-толуол жүйесі, t=60 oC
Идеалды емес ерітінділер болады. Ондайда ерітінді үстіндегі будың қысымы ерітінді ішіндегі заттың концентрациясы бойынша сызықты емес түрде ӛзгереді. Реалды ерітінділердегі қысым
Сурет 3. Бензол-толуол жүйесі, t=60 oC . Бумен судың құрамы, v-cұйық, l – cұйық
Парциалдық қысымдардың ӛзгерісі
Сурет 4 – ацетон –хлороформ жүйесі, t= 35,2 oC.
ацетон –хлороформ жүйесі, t= 35,2 oC. Сұйықтың бетіндегі және будың ішіндегі қысымның ӛзгерісі. Мольдық құрам бойынша ӛзгеріс.
Сурет 5 – Сұйықтағы және будағы парциалдық қысым ӛзгерісі.
Екінші аз мӛлшердегі затқа Генри заңы орынды
𝑝2 =𝐾2𝑥2.
Яғни Генри заңында 
. Оларды аса
сұйық (разбавленный раствор) ерітінді дейді.
П. 12. Теормодинамиалық функциялардың (ТФ) ӛзгерістерін
анықтау. Энтропияға байланысты ӛзгеру бағыты.
Термодинамикадан белгілі келесі шарт. Қайтарымсыз процесстерден шығады
.
(1)
Осыдан
.
Осыдан келесі интегралды функция бар екендігі шығады
.
(2)
Мұнда Т = const. Ол Гельмгольц функциясы деп аталады. Термодинамаикалық функция, термодинамикалық потенциал.
.
V=const болғанда 
. Сонда
.
(3)
(3) маңызды, қайтарымсыз процеске арналған, соны сипаттайды. Кӛлем V – ӛзгермелі болса
,
(4)
немесе
.
(5)
Қысым тұрақты болған жағдайда (5) ті жазамыз
.
(6)
(6) дан келесі функция бар деп айта аламыз
.
(7)
Осыны Гиббс функциясы деп атайды. Бұл екінші рет, теңсіздіктерден, қайтарымсыз процесстен қорытылып шығарылды.
Бір моль газ үшін
.
(8)
(8) ді, (10-7) ні (2) ге қоямыз, (о) таңба стандартты жағдайды кӛрсетеді. Энтропия тең
.
(9)
Келесі формула белгілі
P=RT/V. (10)
(10) ды (9) ға қоямыз
.
(11)
Кӛптеген әдебиетте (11) ді интегралдап сонсон (7) ге және (2) ге қоя бастайды. Біздің ойымызша, одан гӛрі келесі жол тиімді. Сол үшін (9) дағы PdV - ны түрлендіреміз. Сонда болады
.
(12)
(12) негізінде (9) мына түрде жазылады
.
(13)
Біз дәлелдегендей, (7) ге және (2) ге қойып, одан әрі түрлендіруге (13) қолайлы. (13) - ті стандарттық (P0, V0, T0) күйден бастап, кез келген күйге дейін интегралдаймыз
.
(14)
Келесі белгіні еңгіземіз
.
(15)
Келесі формула белгілі
.
(16)
(16) ны (15) ке қоямыз, болады
.
(17)
(17) формула (15) ке қарағанда сәл ықшамдау.
(17) арқылы (14) жазылады
.
(18)
(2) мен (15) ден шығады
Мұнда тұрақтыларды белгілейміз
,
(20)
. (21)
(16)-ны (21) ге қоямыз, болады
.
(22)
(22), (21) мен (19) жазылады
.
(23)
Енді (17) мен (18) арқылы (2) ні қайтадан қорытамыз. Сонда болады
. (24)
(24) тен сол бұрынғыдай, тура (21) дей 
мәні
шығады. Айырмашылық, 
пайдаланып қорытқанда
амалдар қадамы сәл ғана ықшамдау болады.
Енді Гиббс функциясы G ны (22), (23) арқылы қорытып шығарайық.
Анықтама бойынша (7) ні қайтадан жазамыз
.
(7) Осыдан болады
.
(25)
Келесі формуланы пайдаланамыз
.
(26)
(26) ны (25) ке қоямыз. Есептей келгенде болады
.
(27)
Мұнда
.
(28)
Осындағы ( 27), (28) параграф 10 дағы (10-11), (10-12) формулалармен тура бірдей. Осы формулаларды қорыту жолын талдағанда, мынаны байқауға болады. Яғни, бұл интегралды және дифференциалды қорыту жолдары екеуі де бірдей нәтиже беретінін кӛрсетеді. Дегенмен, термодинамикалық функциялардың барлығын (18), (23), (27) түрге келтіргенде дифференциалдық түрден басталатын жол -кейде дұрыс нәтиже бермейді, тиімді емес. Интегралдық ӛрнектерге қарағанда. Интегралдық жол – ұтымды. Осы айтылғанның дәлелі оңай. Мысалы келесі дифференциалды формуланы қарастырайық
.
(5-5)
Бірінші мүшені интегралдағанда болады
.
(29)
Екінші мүше тікелей интегралданбайды, себебі 
- функция
белгісіз. Ал егерде оны интегралдауға интегралданып қойған
(14), (17), (18) ӛрнектерді пайдалансақ – интегралданбайтын
ӛрнекке келеміз.
.
(30)
(30) дың қателігі сол – бір рет интегралданып қойылған ӛрнекті екінші рет интегралдауға болмайды. Дважды нельзя войти в одну и ту же реку деген орыс мақалын осы жерде түсіндім. H, S, U – функцияларды олардың дифференциалдық ӛрнегіненен интегралдап барып табады. Ал F, G – функцияларды тек олардың интегралдық ӛрнегінен анықтаймыз. Термодинамикалық функциялардың осындай ерекшелігі бар. Осыны біз бірінші болып айтып отырмыз.
Осы термодинамикалық функциялардың
температураға байланысты мүшелері 
туралы. G мен S –
екеуіндегі 
тек 
коэффициентпен сипатталады,
F пен H – ол екеуіндегі 
тек қана 
коэффициентпен
сипатталады. 
– функциялардың рӛлі: олар
жәй ғана интегралдау процесінен туған константа емес, олар
сонымен қоса температураға тәуелді функция. Сондықтан
осы коэфициенттің, мүшенің рӛлі екеу. Температураны осы
функцияның параметрі деп қарастыруға болады. Бір
кӛлемде бірнеше әртүрлі газдар болады, сонда жекеленген
компонентаға былай деп жазамыз
,
(31)
мұнда 
компоненталар
индексі. Барлық кӛлемде бір ғана газ болғанда онда
әрине (29) формуланы қарапайымдату үшін 
атм деп
алуға болады, яғни СИ дан бӛлек ӛлшем бірлігіне ауысып.
Алайда, кӛп компонентасы бар қоспадан тұратын газге жеке
бӛлек компонентасына байланысты 
атм деп алуға
болмайды. Жауап – дальтон заңын қарастырыңыз. Тек қана 
атм
болуы мүмкін.
П. 13. Химиялық процесстерде ТФ қолдану.
Келесі химиялық реакцияны қарастырайық
. (1)
A, B, C, D – әртүрлі химиялық
элементтер, 
- мольдық сандар. (10-12),
(10-14), (10-18), (12-27), (12-31) формулаларды осы реакцияға байланысты
жазғанда болады
.
(2)
(2) мынадан шығады
,
,
(3)
,
.
Келесі теңсіздік маңызды болады
.
(4)
Себебі 
, газдардың құрамы
бірдей болса дағы, интегралдаушы константаның мәні
әртүрлі болады, яғни 
.
Мұнда
.
(5)
Сол себептен кейбір әдебиеттерде кездесіп қалатын мынандай теңдеулер қателік болып табылады
,
(6)
. (7)
Дұрысында тек (2), (3)
түрінде жазумыз керек. Яғни 
, тең болмайды. 
-
ол тек G функцияның стандарттық күйдегі ғана
мәні.
тең болады тек бір ғана
дербес ӛте сирек жағдайда
ешқашан тең болмайды, себебі
тең болуы мүмкін тек
қана жалпы қысым 
.
Оған қарағанда 
–
функцияның рӛлі үлкендеу, мүшесі ӛзгеше, ол
температураға байланысты бірнеше функцияның қосындысы.
Яғни ӛзі бӛлек функция. Температура тұрақты
болғанда, ол да тұрақты. Гиббс функциясы G дан
басқа термодинамикада Гельмгольц H, энтропия S, ішкі энергия U –
функциялары кеңінен қолданылады. Осы функциялардың
дұрыстап, тәптіштеп қорытылуы, сипатталуы келесі ғылыми
мақалада жақсы айтылған:
http://elib.sfu-
kras.ru/bitstream/handle/2311/30354/17_Zhakatayev.pdf?sequence=1
https://readera.ru/about-some-properties-and-features-of-differential-andintegrated-representations-146115165
Біздің осы мақала пайдалы болады деп сенеміз.
Бірінші тарауда энтропияның ӛзгерісі маңызды екені айтылған, сол бойынша ∆𝑆 ≥0. Қайтарымсыз процесстерде энтропия ӛседі. Сол сияқты қайтарымсыз процесстерде әрдайым
∆𝐺𝑖 ≤0. (8)
Яғни (8) формула химиялық процесстердің ықтималдық бағытын
кӛрсетеді. Тұрақты ӛзгеріссіз процесстерде
∆𝐺𝑖 =0. (9)
Тарау 3. Химиялық тепе теңдік.
П. 1. Әрекеттенуші масса заңы. Тепе теңдік константа.
Химиялық реакция екі бағытта жүреді: тіке, кері. Мысалға келесі реакцияны қарастырайық
2𝐶𝑂+𝑂2 ↔2𝐶𝑂2 . (1)
Температура, қысымға, заттардың концентрациясына байланысты әрбір бағыттағы реакция жылдамдығы әртүрлі болады. Қосылу, пайда болу реакциясында 𝐶𝑂2 кӛміртегінің диоксиді пайда болады, бұл тіке реакция. Кері реакцияда 2𝐶𝑂2 екі молекулаға, екі затқа жіктеледі. Реакция тіке бағытта жүргенде 𝐶𝑂, 𝑂2 концентрациялары азая бастайды. Соған сәйкес 𝐶𝑂2 концентрациясы кӛбейе бастайды. Кері реакция жүргенде – процесс кері бағытта болады. Температура, қысымға, заттардың концентрациясына байланысты екі бағыттағы реакция жүру тепе теңдік күйге келуі мүмкін.
Сол кезде → оң бағыттағы реакция мен сол бағыттағы ← реакцияның жылдамдықтары теңеседі. Реакция жылдамдығы деген не? Ол заттың пайда болу концентрациясының уақыт бойынша ӛзгерісі
,
(2)
мұнда 𝐶𝑖 - заттың концентрациясы, 1/cm3, моль/см3, 𝜏 - уақыт, сек. Реакция жүргенде заттың концентрациясы азаяды, яғни 𝑑𝐶𝑖 таңбасы минус болады. Сондықтан формула алдында минус қояды, 𝑊𝑖 мәні оң, плюс таңбалы болып шығу үшін.
Екі идеалды газдың реакциясының жылдамдығы олардың концентрациясына пропорционал, (1) ші формуланы қараңыздар.
Сонда тіке бағыттағы реакцияның жылдамдығы тең
.
(3)
𝑛1-CO моль саны, 𝑛2- 𝑂2 моль саны, 𝑘1 - пропорционалдық коэффициент. Сол сияқты кері бағыттағы реакция
.
(4)
𝑘2 - пропорционалдық коэффициент, 𝑛3- 𝐶𝑂2 моль саны. Химиялық тепе теңдік күйде болады
𝑊1 =𝑊2 . (5)
(5) ті (3) пен (4) арқылы жазайық
.
(6)
(6) дан шығады
.
(7)
Заттардың концентрациясы арқылы немесе екі пропорционалдық коэффициенттер арқылы ӛрнектелген (7) формуладағы 𝐾𝑐 тепе теңдік күйдегі константа деп аталады. Константа равновесия. Гульдберг және Вааге деген ғалымдар қорытып шығарған.
Тепе теңдік кезде келесі формула орынды
.
(8)
(8) – келесі формулалардан шығады (т. 2 , 8-11, т. 2, 8-12) [тарау 2 параграф 8 формула 12]. (8) ді келесі түрде жазамыз
.
(9)
(т. 2, 13-1, 13-2, 13-3) формулаларды қарастырайық. Сонда болады
,
,
(10)
,
.
(10) ды (9) ға қойғанда болады
.
(11)
(11) ден шығады
. (12)
Яғни
–
(13)
таза температуралық функция. Тек ғана температураға байланысты функция. Осы функцияның түрі, рӛлі маңызды.
(12) ден парциалдық қысымдар арқылы ӛрнектелген тепе теңдік константасы шығады
.
(14)
(12) кӛрсеткендей ол тек температура функциясы.
(13) ден (7) ге ауысу жасауға болады. Яғни 
дан 
ке ауысамыз. Сол үшін
парциалдық қысымды концентрация арқылы ӛрнектейміз
.
(15)
, 
, 
, 
– заттардың
(компоненталардың) мольдық саны, 
– олардың
кӛлемдік концентрациялары. Келесі формулаларды қараңыздар
(т. 2. 10-19, т. 2. 10-20, т. 2. 10-21). (14) ті (13) ке қоямыз, сонда
, (16)
Мұнда
.
(17)
(16) келесі түрде жазамыз
,
(18)
.
(18) тепе теңдік константа қысым және
концентрация арқылы ӛрнектелгендегі екі түрлі формула
арасындағы байланыс. 
.
болғанда 
, 
болғанда 
. Моль сандары ӛзгермейтін
тұрақты болғанда 
.
Тепе теңдік константалар химиялық реакцияларды есептегенде маңызды роль атқарады. Константалар арқылы химиялық реакцияның құрамын, реакция жасайтын максималды жұмысты есептеуге болады. Тепе теңдік константаларды есептеу жолымен және эксперименталды жолмен анықтауға болады. Олардың мәндері әртүрлі реакцияларға және әртүрлі температурамен қысымға байланысты кӛптеген анықтамалық кітаптарда келтірілген.
Тепе теңдік константаны моль сандарымен ӛрнектеуге болады
Киломоль үлесі кӛлемдік үлеспен ӛрнектеледі
, (19)
-барлық
қоспаның киломоль саны, 
– жекеленген бір
заттың (компонентаның) киломолі, 
- жекеленген бір
заттың (компонентаның кӛлемі) жалғыз ӛзі
ғана болғанда тура сол қоспаның жалпы P
қысымындағы болатын кӛлем. Қосымша келесіні ескереміз
.
(20)
(14)-(20) арқылы 
мен 
, 
арасында байланысты
табуға болады.
(19) ды (13) қойғанда болады
.
(21)
Белгілейміз
.
(22)
Сонда (21) жазылады
. (23)
– формула (17) мен
анықталған, 
- қоспаның жалпы
қысымы, см- орысша смесь деген сӛзден қабылдаған. (13)
ті келесі түрде жазамыз
.
(24)
(24) пен (20) ны (17) ге қоямыз
.
(25)
Белгілейміз
.
(26)
Сонда (25) келесі түрде жазылады
.
(27)
Жинақтай келе жазамыз
.
(28)
(28) – инженерлік тәжірибеде кӛп қолданатын формула.
(28) дегі тепе теңдік константаны реалды газдар
үшін фугитивтілік 
және активтілік 
арқылы
ӛрнектеуге болады.
,
(29)
.
(30)
Тарау 2 п.10 формула (25-27) –ден және осы параграфтағы (9)-(12) формулалардан, фугитивтілік үшін температураға байланысты функцияның келесі түрі шығады
.
)
Идеалды емес, реалды газда (24) формулада келесі коэффициент пайда болады
.
(32)
Мұнда 
- газ идеалды емес,
реалды болғандықтан барлық, барлық концентрация 
толығымен жұмыс жасай
алмайды, толық активті бола алмайтынын кӛрсетеді. 
дің
бір бӛлігі әрекеттенудің потенциалды энергиясына кетеді.
Сондақтын 
- активтілік коэффициенті деп атайды. Ал
келесі шаманы
-
(33)
газдың немесе ерітіндінің активтілігі деп
атайды. Реалды жағдайда 
орнына 
қолданады. Газ идеалдық
күйге жақындағанда 
. Сонда
. (33) ті (12) ге қойғанда
болады
l
.
(34)
Мұнда
(35)
активтілік арқылы ӛрнектелген тепе теңдік константасы. Қысым арқылы жазылған константамен байланысы келесі
.
(36)
(36) тура (28) бен бірдей, 
, 
, 
, 
.
Яғни тепе теңдік константа формула (30) активтілік арқылы ӛрнектелгенде, температураға байланысты функцияда ӛзгеріп келесі түрде болады
l
.
(37)
(28) сияқты, (29), (30) арқылы 
, 
, 
арасындағы
байланысты табуға болады. Сол үшін т. 2 формула (10-25)
пайдаланымыз, және осы параграфтағы (32), (33) ті пайдаланамыз.
Сонда болады
,
(38)
.
(39)
Формулалар (28, 38, 39) –біріккен бір топты құрайды.
П. 2 . Гомогенді реакциялардағы тепе теңдік заңдары
Әсерленуші заттардың барлығы бір күйде, яғни газды күйде болғандағы реакциялар гомогенді деп аталады. Барлығы бір фазада болады. Ондай процесстердің реакцияларын сипаттау оңай, мысалға
2𝐶𝑂+𝑂2 ⇄ 2𝐶𝑂2 +𝑄1.
𝑄1 - бӛлінген жылу мӛлшері. Барлық компонеттер бір газдық фазада болған сон “газ”, немесе “г” деген қосымша белгілер жазылмайды. Реакция тұрақтысы тең
.
П. 3. Гетерогенді реакциялардағы химиялық тепе теңдік.
Бір бірімен әсерленуші заттар әртүрлі фазада болғанда химиялық реакцияны гетерогендік дейді. Алайда олар ерітінді емес. Қысымды анықтағанда үш түрлі қысым пайда болады: газды заттың қысымы, сұйық заттың буы, қатты заттан шыққан газ (оны да “бу” деуге болады). Сұйық пен қатты дененің үстінде қаныққан бу болады. Қаныққан буда қысым тұрақты болады, себебі газда жоғалу – утечка болып жатса, сұйықтан немесе қатты денеден ұшқан, бӛлінген молекулалар сол қысымды қалпына келтіреді.
Тек ғана газдық күйде болған, газдық күйге арналған заттардың парциалдық қысымдары ӛзгереді.
Гетерогендік реакциялардың тепе теңдік константаларын қарастырғанда олардың сұйыққа немесе қатты денеге қатысты жағдайын ескермеуге болады. Себебі ол денелерден бӛлініп шығып, буға, газға айналып (ауысып) кеткен күйді қарастырамыз. Сондықтан барлық реакцияны гомогендік реакция деп, гомогендік фаза деп қарастыруға болады. Сұйықтың немесе қатты дененің буға айналған газын абсолютты қаныққан газ деп есептейді. Яғни оның парциалдық қысымы тұрақты болады. Сол кезде T=const, P = const, жалпы қысым. Қаныққан буда қысым тұрақты болады. Сұйықтан қаншама молекула буға ӛтсен, соншама молекула кері бағытта будан сұйыққа немесе қатты денеге ӛтеді.
Мысал ретінде карбонат кальцийдің диссоциация ыдырау реакциясын қарастырайық
𝐶𝑎𝐶𝑂3,тв ⇄𝐶𝑎𝑂тв +С𝑂2 . (1)
Және угарный газ кӛміртегінің қышқылы (қышқылдануы) реакциясын қарастырайық
𝐶тв +𝐶𝑂2 ⇄2𝐶𝑂. (2)
Тв-твердый сӛзі. (1), (2) реакциялар үшін тепе теңдік константаларды жазайық
,
(3)
.
(4)
𝑃𝐶𝑎С𝑂3,тв, 𝑃𝐶𝑎𝑂тв,𝑃𝐶тв - бұлар карбонат кальцидің, кальцидің қышқылы, кӛміртегінің молекулалары мен атомдарының қаныққан будағы парциалдық қысымы, олар тұрақты, ӛзгермейді, жоғарыда айтылған себептен. Сонда (3) пен (4) келесі түрде болады
.
(5)
Осы реакциялардың тепе теңдік константалары бірқалыпты 𝑃𝐶𝑂2 және
𝑃𝐶𝑂 +𝑃𝐶𝑂2 парциалдық қысымдармен анықталады. Осындай бірқалыпты парциалдық қысымдар диссоциация қысымы немесе диссоциация серпімділігі деп аталады. Кейбір реакцияға арналған тепе-теңдік константалар келесі 1 кестеде кӛрсетілген. Кесте 1.
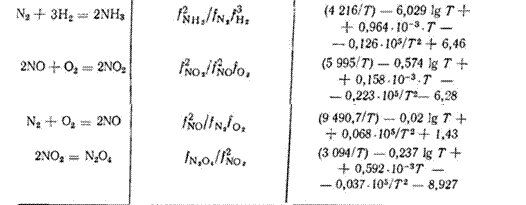
Кесте 2
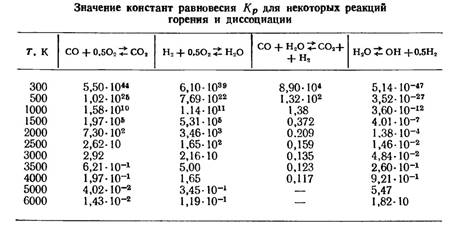
Диссоциация қысымы тек температураға байланысты ӛзгереді. Диссоциация қысымы 0,1 МПа жеткендегі температура – диссоциация температурасы деп аталады.
Келесі мысал ретінде домна пешінде ӛтетін келесі реакцияны қарастырайық
𝐹𝑒𝑂+𝐶𝑂 ⇄𝐹𝑒𝑂+𝐶𝑂2 . (6)
Парциалдық қысымдарды белгілейміз 𝑃𝐹𝑒𝑂 , 𝑃𝐶𝑂, 𝑃𝐶𝑂2, 𝑃𝐹𝑒 . Тепе теңдік константа
.
(7)
𝑃𝐹𝑒𝑂 =const, 𝑃𝐹𝑒 =𝑐𝑜𝑛𝑠𝑡 болғандықтан (7) де осы екеуін алып тастаймыз. Сонда
. (8)
Сол сияқты
.
(9)
(8), (9) реакция (7) нің тепе теңдік күйін толық сипаттайды. Жалпы жағдайда
(10)
Мұнда гет – гетерогендік, қатты фаза, ал қосымша белгісі жоқтар – газды фазалар. Сонда реакцияның тепе теңдік константалары болады
,
(11) 
.
П. 2, 3 – терде қарастырылған реакцияның тепе теңдігінен шығатын заңдылықтарды – әркеттенуші масса заңдары дейді, закон действующих масс.
Гетерогенді ортада фазалар ауысатын жерде, шекаралық жұқа қабат пайда болады, сол жерде адсорбциялық процесстер жүреді. Сонда реакция жылдамдығы сол адсорбциялық қабаттағы компонеталардың концентрациясымен анықталады. Яғни негізгі реакциялар шекаралық қабатта ӛтеді.
Дизель цилиндрінде сұйық отын тамшылар түрінде шашырайды. Әрбір тамшының бойында адсорбциялық қабат болда. Реакциялар сонда жүреді
,
(12)
- реакция
жылдамдығының шын константасы, 
- отынның
концентрациясы, 
- адсорбциялық
қабаттағы оттегінің концентрациясы, 
- реакция
жылдамдығы, 1/сек. Алайда адсорбциялық шекаралық
қабатта 
белгісіз болады. Сондықтан газды
ортадағы концентрацияны 
ні есепке алады.
Сонда реакция жылдамдығы
.
(13)
𝐶𝐵 , 𝐶𝑂2 – компоненталардың нормальды концентрациялары, реакциялардың жылдамдығы, 𝑘 - жылдамдықтың кӛрінімді (кажущаяся константа скорости реакции) константасы.
Физикалық жағдайға, кӛрініске (12) жақын болғанымен, алайда есепетеуде (13) жақсы. Себебі ол шынайы газдың концентрацияларымен жұмыс жасайды.
Екі мысал қарайық.
1. Домна пешіндегі келесі реакцияға байланысты қоспаның құрамда- рын анықтау керек.
𝐹𝑒𝑂+𝐶𝑂⇄𝐹𝑒+𝐶𝑂2 .
Температура 𝑡 =1000 oC, тепе теңдік константа 𝐾𝑃 =2,5.
Реакция гетерогендік, сондықтан 𝐹𝑒𝑂 және 𝐹𝑒 концентрациялары тұрақты. Оларды ескермейміз. Және де ∆𝑛=0 болғандықтан 𝐾𝑃 =𝐾𝐶. Сондықтан
.
CO ның реакция түскен проценттік шамасын Х деп белгілейік. Кӛлемдік концентарция бойынша проценті. Тепе теңдік күйге жақындағанда газдың қоспасында болады, процент бойынша
𝐶𝑂 =100−𝑋 , 𝐶𝑂2 =𝑋.
Сондықтан
=2,5.
Осыдан
𝑋 =28,6 %.
Енді тепе теңдік кезде мӛлшерлер болады
𝐶𝑂=100−𝑋 =100−28,6=71,4 % .
𝐶𝑂2 =𝑋 =28,6 % .
2. Келесі реакцияға
𝐶+𝑂 =𝐶𝑂2
тепе теңдік константасын табу керек? Мұнда температура 𝑡 =1300 oC, 𝐶𝑂2 - кӛлемдік концентрациясы 22,5 % .
Реакция гетерогендік, 𝐶 концентрациясы тұрақты, сондықтан оны теңдеуге еңгізбейміз. Сондықтан
.
Және де ∆𝑛=0 болғандықтан 𝐾𝑃 =𝐾𝐶 . Сондықтан
.
П. 4. Химиялық реакцияға байланысты термодинамиканың
бірінші заңы.
Барлық химиялық реакциялар жылуды не бӛліп шығарады, немесе жұтады. Сырттан жылуды қабылдайды. Жылуды бӛліп шығаратын реакциялар экзотермиялық деп аталады, ал сырттан келген жылуды қабылдап, бойына сіңіріп, “жоқ қылып” алатын реакцияны эндотермиялық деп атайды.
Мысалға су тегі жанып судың пайда болу реакциясы экзотермиялық реакция
.
Су тегі мен кӛмір тегінің қосылу реакциясы эндотермиялық реакция
2С+𝐻2 =𝐶2𝐻2 −54000 кал/моль .
Реакциялар жүріп жатқан жүйеге термодинамиканың бірінші заңын
𝑄 =∆𝑈+𝐴+𝐿 .
𝐿 - таза механикалық жұмыс, 𝐴 - жұмыстардың басқа түрі, мысалға электрлік жұмыс, магниттік жұмыс, кӛлемдік поляризациалану жұмыс, электр, магнит ӛрісінде индукция, ӛздік индукциялану, т.б. жұмыстар түрі. Химиялық реакцияларға байланысты қосымша келісілген шартты қарастыру керек:
+𝑄 ӛндірілген, шығарылған жылу
−𝑄 реакцияға түсуші заттардың бойына, жүйе ӛзіне жұтып алған жылу, жұмсалған жылу. Яғни сыртқы ортаның осы жүйеге берген жылуы.
+∆𝑈 ішкі энергияның азаюы, 𝑈2 <𝑈1. Минус (-) таңбада – керісінше. +A немесе +L – жүйе ӛзі жасаған механикалық жұмыс, сыртқы орта емес.
Физикалық химия, химиялық термодинамика курстарында химиялық реакция арқылы жасалған механикалық жұмыс әдетте А деп белгіленеді. Алайда кӛптеген әдебиетте, әсіресе техникалық термодинамика курстарында ортаның (жүйенің) жасаған жұмысы әдетте L деп белгіленеді. Ойда сақтап, ұмытпау керек, негізінде екеуі бір жұмыс. L – негізінде газ кӛлемі атқарған таза механикалық ғана жұмыс, мысалға кӛлем ӛзгереді, поршень итереді, қалақ айналдырады. Оған қарағанда А жұмыстың ауқымы кеңдеу. Ол жұмысқа қосымша (механикалықтан басқа) электрлік, жарық ӛндіру, поляризациялану, магниттік энергияның пайда болуы, т. б. механикалық емес жұмыстардың түрлері кіреді. Мысалға электрлік, немесе магниттік энергияға айналуы, перезарядка конденсатора, т. б. Техникалық термодинамикада заттың мӛлшері негізінде килограммен (кг) ӛлшенеді, соған қатынастырады. Ал мұнда, физикалық химия мен химиялық термодинамикада зат кӛлемі, масса – зат мӛлшері – мольмен ӛлшенеді, соған қатынастырады.
Сол себептен жылу сыйымдылықты (жылу сйымдылық коэффициентін) килограммға емес – зат мӛлшері мольге қатынастырады. Оны 𝐶𝑃,𝜇 , 𝐶𝑃 , 𝐶𝑉,𝜇 , 𝜇𝐶𝑉 деп белгілейді, кӛп жағдайда 𝜇 таңбасын жазбайды, 𝐶𝑉 , 𝐶𝑃 деп жазады.
Химиялық реакцияға, жану процесстеріне байланысты термодинамиканың бірінші заңын келесі түрде жазады
∆𝑈 =𝑄+𝐴, (1)
∆𝑈 - ішкі энергияның ӛзгеруі, 𝑄 - реакция жылуы, А - реакция жұмысы, барлығының ӛлшем бірлігі Дж.
Элементарлы процесске жазылады
−𝑑𝑈=𝑑𝑄+𝑑𝐴. (2)
(2) формулада U дың алдында минус пайда
болады. Себебі дифференциалдық теңдеу заңы бойынша
әрбір dU ӛсіп отырған функцияға жазады. Математика
заңы бойынша 
.
Алайда химиялық тұрғыдан 
>0 болу үшін 
себебі химиялық жағдайда
әрдайым 
болу керек.
Механикалық жұмысты L, жұмыстың
басқа түрлерін 
деп белгілейік.
Сонда (1), (2) келесі түрде жазылады
,
(3)
,
(4)
.
(5)
.
(6)
(6) – толық жұмыс, жіктемей бірге жазғанда.
(3) - (4) кӛрсеткендей ішкі энергия 
мен 
арасында
әртүрлі болып таралады. Опытқа байланысты. Толық
қайтарымды реакцияларда жұмыс максималды болады 
,
ал шығарылған жылу ең аз, минималды болады 
.
Осы жағдайға байланысты
.
(7)
Екінші жағдайда атқарылған жұмыс ең аз, минималды болады, мысалға тек ғана газдың кӛлемінің ұлғаю жұмысы болады. Сол кезде атқарылған жұмыс ең тӛмен, ал шығарылған жылу мӛлшері ең жоғары болады
.
(8)
Соңғы жағдайда, (8) дегі 
- болған реакцияның жылу
эффектісі деп аталады.
-
кӛлемнің ұлғаюның механикалық жасалған жұмысы. Ішкі энергия U келесі құрамда болады
.
(9)
– атом, молекуланың
кинетикалық энергиясы, 
- потенциалдық
энергия, оған электрлік әсерлесу, магниттік әсерлесу, лездік
поляризациялану арқылы әсерлесу, т.б. сондай физикалық
әсерлесу энергиялары кіреді, 
– Альберт
Эйнштейннің
теориясы бойынша әрбір затта, денеде, молекулада бар толық энергия түрі. Ол массамен байланысты. Сол бойынша әртүрлі химиялық реакциялар жүргенде ӛте аз мӛлшерде болса дағы масса ӛзгеруі мүмкін
.
(10)
Классикалық опыт (тәжірибе)
шеңберінде химиялық реакцияларда 
масса ӛзгерісі
байқалмайды. Алайда атомдық физикада, ядролық химияда
кӛп мӛлшерде энергияның пайда болуы тек ғана (10)
формула негізінде түсіндіріледі. Яғни реакцияға дейінгі
заттардың жалпы массасы реакциядан кейінгі молекулалардың
(атомдардың) жалпы массасынан аздаған айырмашылықта болады.
Не аз, кем, немесе артық (үлкен) мӛлшерде болады.
П. 5. V=const болғандағы химиялық
реакцияның жылулық эффектісі.
Химиялық реакция қатты заттар, немесе сұйықтар арасында жүргенде кӛлем ӛзгермейді. Газдардағы реакциялар ыдыстың ішінде жүргенде кӛлем ӛзгермейді. Сол кезде dV=0. Және де
Сондықтан
.
(1)
– тұрақты
кӛлемдегі реакцияның жылулық эффектісі. Ол ішкі
энергияның ӛзгерісіне тең.
П. 6. P=const болғандағы химиялық реакцияның жылулық эффектісі.
Қысым тұрақты болғанда термодинамиканың бірінші заңы
.
(1)
- тұрақты
қысымдағы химиялық реакцияның жылулық эффектісі.
(1) ді келесі түрде жазамыз
.
(2)
(2) ден болады
,
. (3)
Мұнда 
, 
-
энтальпия.
П. 7. 
және 
арасында байланыс.
Әртүрлі жағдайда ӛткен
химиялық реакциялардың жылулық эффектілері де 
және
әртүрлі болады.
Тұрақты қысымда жылудың бір бӛлігі кӛлем
ӛзгергендегі жұмысқа кетеді.
Химиялық реакцияларда заттардың мӛлшерлері (моль саны) ӛзгеріп жатады. Компоненталарға идеалды газдардың заңдарын қолданып жазамыз
.
(1)
– газды заттардың реакцияға
дейінгі, реакциядан кейінгі моль саны, 
- моль санының
ӛзгерісі, R –универсалды газ тұрақтысы.
Жоғарыда айтылған бойынша
,
(2)
.
(3)
(1) – (3) тен шығады
,
.
(4)
(4) негізінде 
пен 
арасындағы
қатынасты табуға болады, қайсысы үлкен? Химиялық
реакциялар соңында 
болса, онда заттар саны ӛсіп
жатады, ал 
. Бұл оң жұмыс жасау
үшін энергия жұмсалады дегенді білдіреді. R=2 кал/моль.
Дәлірек айтсақ R=1,985 кал/моль.
болғанда,
керісінше 
. Мұнда зат саны азаяды,
кӛлем кішірейеді. Кӛлем сығылуы қосымша энергияны керек
етеді, жұтады. Жүйенің ішкі энергиясы азаяды. Қысым
тұрақты болғандағы ішкі энергия ӛзгерісі,
кӛлем тұрақты болғандағы ішкі энергияның
ӛзгерісіне тең емес 
. Сондықтан
.
(5)
(5) ті (6-1) ге қоямыз. Сонда
.
(6)
Конденсацияланған,
сұйықты ортада 
және
арасында айырмашылық аз, жуықтағанда
. Газды ортада бұл
айырмашылық әсерлі болады.
Есеп 1. Микстер тәжірибе (эксперимент) жасаған. Калориметрикалық бомбада тұрақты кӛлемде су тегі жанған. Нәтижесінде су пайда болған. Шыққан, ӛндірілген жылу эффекті тең
.
P=const , T=291 K болғанда Томсон опыттары осы реакцияға береді
.
Осыдан
= 
1680 кал. (5)
Қарастырған реакция мынандай
+
Q. (6)
Сонда
.
Пайда болған судың кӛлемін ӛте аз, ноль деп қабылдаған, газдың кӛлемімен салыстырғанда. Ал реакцияға дейінгі газдар мӛлшері 3 моль. Соңында
𝑄𝑃,𝑚𝑎𝑥 −𝑄𝑉,𝑚𝑎𝑥 =2∆𝑛𝑇=-2·(-3)·291=1740 кал. (7)
(5) пен (7) ні салыстырсақ, қанағат, жеткілікті ретінде дәл деп айтамыз. Есеп 2. Келесі реакцияны қарастырамыз
.
(8)
Эксперимент, опыт бойынша 𝑄𝑉,𝑚𝑎𝑥 =68000 кал/моль. Мұнда t=20 oC.
Осы деректер бойынша 𝑄𝑃,𝑚𝑎𝑥 табу керек?
Зат саны ӛзгерісі
.
Сондықтан
293 =
68293 кал/моль.
Есеп 3. Келесі реакцияны қарастырамыз
.
(9)
Опыт бойынша 𝑄𝑉,𝑚𝑎𝑥 =26000 кал/моль. Мұнда t=20 oC. Осы деректер бойынша 𝑄𝑃,𝑚𝑎𝑥 табу керек?
Кӛміртекгі қатты зат, 𝐶тв . Оның кӛлемін ескермейміз, тең 0, газдармен салыстырғанда. Моль ӛзгерісі
.
Сонда болады
кал/моль.
Есеп 4. Келесі реакцияны қарастырамыз
𝐶тв +𝑂2,газ =𝐶𝑂2,газ + Q.
Опыт бойынша 𝑄𝑃,𝑚𝑎𝑥 =94000 кал/моль. Мұнда t=15 oC. Осы деректер бойынша 𝑄𝑉,𝑚𝑎𝑥 табу керек?
Кӛміртекгі қатты зат, 𝐶тв . Оның кӛлемін ескермейміз, тең 0, газдармен салыстырғанда. Моль ӛзгерісі
∆𝑛=𝑛2 −𝑛1 =1−1=0 .
Сонда болады
𝑄𝑉,𝑚𝑎𝑥 =𝑄𝑃,𝑚𝑎𝑥 =94000 кал/моль.
Есеп 5. Кӛлемдері 1 м3 СО және H2 газдардың қысым тұрақты 1 атм, t=15 oC болғандағы жылу ӛндірісін (теплотворная способность топлива) анықтау керек? Келесі екі шама белгілі болғанда
𝐻𝑉,𝐶𝑂 =2800 кал/м3 , 𝐻𝑉, 𝐻2 =2800 кал/м3 .
Жылу ӛнімділік деп 1 кг салмаққа немесе 1 м3 кӛлемге шаққандағы отынның ӛндіретін, шығаратын жылу мӛлшерін айтады, QV = Дж/м3, QM= Дж/кг.
Қысым тұрақты болғанда Юнкерс калориметрімен анықтайды, ал кӛлем тұрақты болғанда Крекер бомбасында анықтайды.
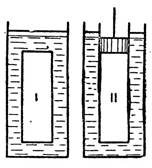
Сурет 1 - QV, QM анықтайтын Крекер (1), Юнкерс (2) құралдары.
Бірінші ыдыста кӛлем тұрақты,
екінші ыдыста қысым тұрақты. Жылу ӛндірісін 𝐻𝑉, 𝐻𝑃
анықтағанда жанып болған продуктілерді ӛнімдерді
реакцияға дейін болған темпераутраға дейін суыту керек.
Яғни болған, шыққан ӛнімдегі ішкі энергияны да
есептеуіміз керек. Сол кездегі ӛлшеген 𝑄𝑉
=𝐻𝑉, 𝑄𝑃
=𝐻𝑃. Реакцияда шығарылған
жылу мӛлшері отынның жылу ӛндіргіштік мӛлшеріне
тең болады. 𝐻𝑉
- бірінші ыдыста анықталады, 
- екінші ыдыста.
Қысым тұрақты болу үшін поршень еркін
қозғалады. Осыдан 
кӛрінеді.
Себебі P=const болғанда кӛлем ӛзгереді, яғни
жұмыс жасалады. Жасалған жұмыс қосымша жылу
мӛлшерін жұмсауды қажет етеді.
Термодинамиканың бірінші заңы бойынша келесі формулалар белгілі
,
,
.
Сол сияқты жылу ӛндірісіне болады
,
.
- жану процесі болғандағы
кӛлемнің ӛзгеруі. 1 м3 CO жанғанда
. Формула (8) қараңыздар.
Сондықтан
.
(10)
1 м3 жанғанда 
жанғанда,
. Реакция
.
Сондықтан
.
(11)
(10), (11) кӛрсеткендей, 
, 
арасындағы айырмашылық 0,5
1,5 % . Сондықтан айырмашылық жоқ, бірдей деп есептейміз.
а)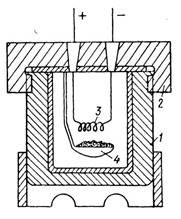 
б)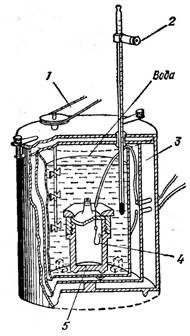 
а) 1-қалың қабырғалы цилиндр, 2 – алынбалы қақпақ, 3- сымды спираль, қыздырғыш, 4 – чашка (ыдыс).
б) 1-ременьді айналдырушы, 2 – термометрді бақылаушы лупа, 3 – ауа толған қуыс, 4 – сымды спираль, қыздырғыш, 5 – реакциондық камера -
“бомба”.
Сурет 2 – Калориметрикалық камера түрлері.
П. 8. Жанудың, заттың пайда болуының стандартты жылу мӛлшері.
Гесс заңы.
Сутегінің қышқылдану, яғни жану реакциясын қарастырайық
,
(1)
.
(2)
Екі жағдай болуы мүмкін. (1) де 𝐻2𝑂г газ түрінде болады, сонда бӛлінген, шығарылған жылу 𝑄төм - тӛменгі мәнге ие болдаы. (2) – де 𝐻2𝑂ж - сүйық түрде, яғни барлық булар конденсацияланып су түріне ауысты, мұнда “ж” – жидкий деген сӛз. Сонда бӛлінген, шығарылған жылу 𝑄жоғ - тӛменгі мәнге ие болады. Мұнда 𝑄төм =57800 кал/моль , ал (2) дегі шығарылған жылу мӛлшері үлкендеу, кӛптеу болады 𝑄жоғ =68200 кал/ моль. 1 кал = 4,19 Дж.
𝑄төм , 𝑄жоғ анықтағанда 𝑡г =𝑡в =0 𝑜𝐶, P=101,3 кПа , V= 1 м3.
Маңызды газдардың техникалық сипаттамалары 1ші кестеде.
Кесте 1
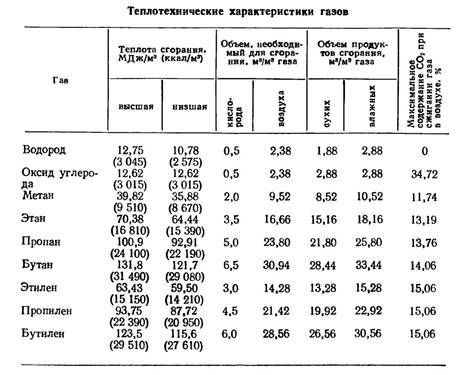
Г. И. Гесс заңы. Химиялық реакцияның жылу ӛндіру (шығару) бойынша нәтижесі жүріп жатқан реакциялардың аралық, ортаңғы күйлеріне (сатыларына) байланысты емес, ол тек бастапқы, сонсон ең соңғы күйге, бастапқы мен соңғы кездегі элементтерге, молекулалар түрлеріне, пайда болған заттарға ғана байланысты.
Бұл заңды 1840 ж. орыс ғалыми, академик Гесс ойлап, тауып дәлелдеген. Мысал ретінде келесі реакцияны қарастырайық
.
(3)
𝑄1 - ді эксперименттен анықтауға келмейді, қиын, себебі қосымша 𝐶𝑂2 пайда болады. Алайда келесі екі реакциядағы 𝑄2 , 𝑄3 тәжірибеден анықтау оңай
,
(4)
𝐶+𝑂2 =𝐶𝑂2 +𝑄3 . (5)
𝑄1 = 26000 кал/моль, 𝑄2 =68000 кал/моль, 𝑄3 =94000 кал/моль. Гесстың заңы бойынша 𝑄1+𝑄2 =𝑄3. Осыдан 𝑄1 =𝑄3 −𝑄2 = 26000 кал/моль.
Осы Гесс заңын келесі сурет сипаттайды
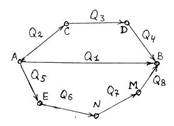
Сурет 1 – Гесс заңына түсініктеме сызба.
𝑄1 - A-B тікелей реакцияның ӛндірілген жылуы, A-C-D-B және A-E-N-MB – параллельді, альтернативті екі жол. Сонда Гесс заңы бойынша
𝑄1 =𝑄2 +𝑄3 +𝑄4 ,
𝑄1 =𝑄5 +𝑄6 +𝑄7 +𝑄8.
Гесс заңы тұжырым ретінде айтылғанда А мен B заттар – олар ӛздері күрделі (құрамды) заттар болуы мүмкін. А мен B құрамы ӛздері қалай пайда болды, олардың, құрамды бӛліктері пайда болғанда қандай жылу шығарылды немесе жойылды (жұтылды) ? – ол туралы Гесс заңында айрықша айтылмайды. Ол ойды, ол тұжырымды Гесстің заңынының 4-ші салдары деп жеке дара бӛліп, ерекше мән беріп айтады. Ол туралы – кейінде айтамыз. Екінші сӛзбен айтсақ – шекаралық, шеткі жағдай (граничное условие) ерекшеленіп айтылады.
Гесс заңынан келесі 4 салдар (следствие) шығады.
1. Заттың ыдырау, жіктелу (разложение) жылу эффектісі сол заттың қосылу, пайда болу жылу эффектісіне тең
𝑄разл =−𝑄образ .
2. Мысалға, A дан - B шығады, С дан – B шығады. А мен С – бастапқыдағы екі бӛлек боп тұрған, әртүрлі заттар, әртүрлі жүйелер. Екі нүктеден шығып (А, С) бір нүктеге (В) келген екі жол, сурет 2.
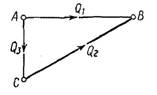
Сурет 2 - Үш сатылы реакция жолы.
Сонда 𝑄1 =𝑄2 +𝑄3. Осыдан А дан - C элементі пайда болғандағы ӛндірілген реакция жылуын табуға болады 𝑄3 = 𝑄1 −𝑄2. Берілген Q лар арқылы белгісіз Q ды табуға болады. Математикаға ұқсайды. Теңдеулерді бір-біріне қоя отырып белгісізді (неизвестная величина) табуға болады.
3. Мысалға, A дан - B шығады, А дан – С шығады. Соңында пайда болған B мен С – екі бӛлек, әртүрлі заттар, әртүрлі жүйелер. Бұл бір нүктеден (А) шығып екі нүктеге (В, С) келген екі жол, сурет 3.
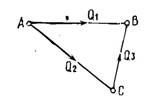
Сурет 3 -Үш сатылы реакция жолы.
Сонда 𝑄1 =𝑄2 +𝑄3. Осыдан С дан - В элементі пайда болғандағы ӛндірілген реакция жылуын табуға болады 𝑄3 = 𝑄1 −𝑄2. Берілген Q лар арқылы белгісіз Q ды табуға болады.
Пайда болу жылуы. Кӛптеген заттар, элементтер химиялық реакция негізінде пайда болады. Барлығы жана бермейді. Жанусыз ӛтетін реакциялар кӛп. Бірақта, қалай дегенмен заттар, элементтер бір бірімен қосылып басқа заттар, элементтер пайда болып жатқанда жылу не ӛндіріледі, бӛлінеді. Не болмаса жылу жойылады, жұтылады.
Кӛптеген заттардың, элементтердің пайда болу, немесе ыдырау жылуы стандартты жағдайға байланысты кесте түрінде келтірілген. Сонда температура 𝑇ст =298,15 K, 𝑃ст =1,013∙105 Па = 760 мм.рт.ст.
Бірнеше қарапайым заттарға, элементтерге (𝐶,𝐻2,𝑂2,𝐶𝑙2,г ,𝐹2,г ,т.б.) пайда болу жылуы ноль 0 деп қабылданған. Басқа заттардың (күрделі элементтердің, күрделі молекулалардың) пайда болу жылуы (жылулық эффектісі) үш түрмен анықталады: 1) осы қарапайым элементтерден құралады. 2) эксперимент негізінде анықталады. 3) Теориялық есеп бойынша анықталады.
Пайда болу энтальпия ∆𝐻обрст туралы толықтау мәліметтерді: Равдель А.
А., Пономарева А. М. “Краткий справочник
физико-химических величин” кітаптан табасыздар. Ондай толық
анықтамаларда 
пен қоса пайда болу энтропиясы да
беріледі ∆𝑆обрст
. Сонда пайда болудың термодинамикалық Гиббс потенциалы келесі
формуламен есептеледі
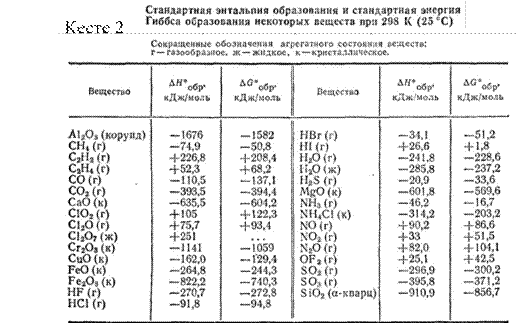
∆𝐺обрст =∆𝐻обрст −𝑇∆𝑆обрст . (6)
Гесс заңының 4-ші және 5-ші салдары бар. Соларды қарастырайық. Екі күрделі зат химиялық реакцияға түсіп соңында 3-ші және 4-ші күрделі заттар пайда болды.
𝛼𝐴+𝛽𝐵=𝛾𝐶+𝛿𝐷+𝑄𝑃.
Осы реакцияның пайда болу жылуы
.
(7)
(7) ні жалпылап жазады
.
(8)
- шыққан ӛнім, орысша
продукт, пайдала болу (образование) жылуы, 
- реакция
басталғанға дейінгі, бастапқы, исходный заттардың пайда
болу жылуы, 𝑛𝑖-
моль сандарының кӛрсеткіші.
(8) ді былай түсінеміз. Шыққан ӛнімдердің (заттардың) пайда болу жылуынан бастапқы заттардың пайда болу жылуын алып тастаса – химиялық реакцияның жылу эффектісі (нәтижесі) шығады. Осы Гесс заңынан шыққан 4 ші салдары.
Элементтердің пайда болу жылуына байланысты
Гесс заңы және оның түгел 4 салдары жану реакциясына да
байланысты орындалады деп есептейді. Жану реакциясы жылуына 
байланысты
Гесс заңдары басқа да химиялық реакциялардағы пайда
болу (немесе жойылу) жылуларына 
байланысты,
энтальпияға 
, энтропияға 
,
Гиббс функциясына 
- толығымен орындалады.
(8) ші формуланы таза, тек ғана жану процесіне байланысты жазады
.
(9)
Бұрынғыдан ерекшелік, бастапқы заттарда жанудан пайда болған, реакция нәтижесі де, продуктілер – олар да жану нәтижесінде пайда болған. сгор. – сг. - сгорание - жану. Осы тұжырымды Гесс заңынан шыққан 5 ші салдар деп атайды.
П. 9. Есеп шығару үлгілері.
Есеп 1. Идеалды газдың алғашқы
күйінде: 
, 
,
.
Содан кейін газ сығылады, кӛлемі 
. болады. Анықтау
керек: температура қаншаға кӛтеріледі, сығуға
жұмсалған жұмыс қандай болады? Шешімі:
Адиабаталық процесске болады:
Атқарылған жұмыс табылады формуладан
.
Моль санын келесің формуладан табамыз
.
Атқарылған жұмыс табылады формуладан
.
Бір атомды газге 
, R=0,082 л
), 
. Сонда (бірінші жағдайда) бір
атомды газге
ккал.
Екінші жағдайда екі атомды газге 
=
1,4 , 
.
ккал.
Газдың молекуласының құрамы күрделенген, ӛскен сайын адиабаталық сығылуға жұмсалған жұмыс азаяды, және температура ӛсуі де тӛмендейді.
Есеп 2. Идеалды газдың кӛлемі 
, 
. Адиабаталық
кеңеюден кейін болған кӛлем: 
. Сондағы температура 
. Екі жылу сыйымдылықты табу керек 
, 
?
Шешімі.
Адиабата коэффициентін табамыз
Келесі екі теңдеуді жүйе (система) ретінде қарастырамыз және шешеміз:
,
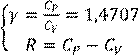≈5 , 
≈7.
Есеп 3. Су тегі массасы m=3 г, қысымы 
, температурасы 
. Қысым ӛзгермеді 
. Кӛлем ӛсті де 
болды.
Газдың жасаған жұмысын А, ішкі
энергия ӛзгерісін 
және қабылдаған жылу
мӛлшерді 
табыңыздыр?
Шешімі. Кӛлемді табамыз
.
Жұмысты табамыз
=41,5 л·атм.
. Екінші температура
табамыз
.
Содан қабылданған жылу мӛлшерін табамыз
кал.
Ішкі энергияның ӛзгерісі тең
= 2536
кал.
Мұнда
,
,
.
Есеп 4. Газ күйіндегі 
сутегінің
жылу сыйымдылығының температураға байланысты формуласы
берілген 
. Температура t=1000 oC
болғандағы 
, 
,
, 
табыңдар, бір мольға
қатысты?
Шешімі.
.
.
Сондықтан орташа жылу сыйымдылық болады
.
Содан сон
.
.
Меншікті жылу сыйысдылықты табу үшін молярлық массаға M=2 грам/моль бӛледі
. 
.
.
Есеп 5. t=100 oC болғанда
темірдің меншікті жылу сыйымдылығы 0,1124 
. t1=0
oC тен t2=100 oC аралығында орташа
меншікті жылу сыйымдылығы 0,1089 
. Меншікті жылу
сыйымдылықтың температураға байланысты ӛзгерісін табу
керек?
Шешімі
Келесі теңдеулер белгілі
,
.
Осыдан 
, 
мәндерін
табамыз
; 
.
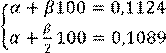
Соңында
.
Есеп 6. Қысым тұрақты
болғанда 
кӛмір қышқылды
газдың меншікті жылу сыйымдылығы 0,217 кал/(г
).
Сонда 
=?
Қатынасын табыңыздар.
Шешімі
Меншікті жылу сыйымдылығы коэффициенті арқылы молярлық
(молекулярлық) жылу сыйымдылықты табамыз
Енді 
табамыз
=9,548 –
1,987 = 7,561 кал/(моль·град).
Соңында адиабаталық коэффициентті табамыз
.
Есеп 7. Массасы 200 г
кӛмірдің екі қышқылды газының 
молекулярлық
жылу сыйымдылығының формуласы келесі
.
Температура 27 oС тан 227 oС ке дейін қыздыру үшін қаншама жылу мӛлшері керек? Екі жағдайда табу керек: 1) қысым тұрақты, 2) кӛлем тұрақты. Шешімі.
Берілген коэффициенттер мәні: 
, 
, 
. Осыдан табамыз 
. Температураларды Кельвинге ауыстырамыз 
. 
.
Сонда орташа жылу сыйымдылық болады
кал/(моль·град).
Содан сон табамыз
= 8670 кал.
= 9,536 – 1,987=7,549
кал/(моль·град).
табамыз
= 6863 кал.
Мынаған назар аудару керек 
.
Тұрақты қысымдығы жылу мӛлшері
тұрақты кӛлемдегі жылу мӛлшерінен
кӛп.
Есеп 8. Қорғасын қышқылы
пайда болу жылуы 
, судың буы 
пайда болу
жылуы 
, қорғасынның екі
мәрте қышқылы 
Су тегі 
мен 
арасындағы реакция, яғни
келесі
реакцияның жылу эффектісін табу керек 
.
Шешімі.
Берілгендер
,
(1)
,
(2)
.
(3)
Гесс заңының тӛртінші салдарынан болады
.
Есеп 9. Судың және кӛміртегінің екі мәрте қышқылының стандартты
пайда болу жылуы берілген. 
, 
. Метанның
стандартты жану температурасы берілген 
. Метанның
қарапайым заттардан құралғандағы
пайда болу жылуын табу керек? Екі жағдайда: тұрақты кӛлем, тұрақты қысым. Шешімі.
Келесі теңдеулер белгілі
,
(4)
,
(5)
(6)
(4) - ті 2-ге кӛбейтеміз, (5) ке қосамыз. Нәтижеден (6) ны аламыз.
Сонда болады
кал/моль.
Нәтижеде, тұрақты қысымда
.
Тұрақты кӛлемдегі жылуды табамыз
кал/моль.
(7)
Осы есепте Гесс заңының 5-ші салдары қолданды.
Есеп 10. Келесі пайда болу
жылулары берілген: 
, 
кал/моль. Келесі
реакцияға
(8)
Энтальпия 
және ішкі
энергия 
ӛзгерістерін табу керек?
Шешімі.
Гесс заңының 4 салдарынан болады
кал/моль
кал/моль
-202180 – (2-3) ·1,987·298 = - 201588 кал/моль.
Есеп 11. Келесі реакциялар және жылулар белгілі:
,
(9)
кал
, (10)
кал. (11)
Табу керек: газды аммиактың пайда болу жылуын, аммиактың судағы ерітіндісінің пайда болу жылуын.
Шешімі.
(9) ды +1/4 ке, (10) ды +3/4 ке кӛбейтеміз, сонсон бір-біріне қосамыз, болады
кал.
(12)
(11) мен (12) қосқанда болады
кал.
Есеп 12. Қысым тұрақты болғанда газды бромдық сутегінің HBr, газды бромның және сутегінің жылу сыйымдылығы температураға байланысты келесі формулалармен сипатталады:
,
,
.
Бромды сутегінің пайда болу жылуының температураға байланасты
қалай ӛзгеретін функцияны табу керек, 
? Табу керек
? Мұнда егер белгілі болса 
.
Шешімі.
Келесі реакциядағы
.
жылу сыйымдылықтардың қосындысын табамыз
. (13)
Келесі теңдеуге
(14)
(13) ті қоямыз, болады
.
Осыдан кейін температура T=1000 K
болғандағы 
пайда болу жылуын есептейміз
кал/моль.
Есеп 13. Қысым тұрақты болғанда аммиактың молекулярлық
(мольдық) жылу сыйымдылығы келесі теңдеумен сипатталады
.
Азоттың кӛлем тұрақты болғандағы молекулярлық жылу сыйымдылығы
.
Су тегінің тұрақты болғандағы молекулярлық жылу сыйымдылығы
.
Аммиактың қысым тұрақты,
температура 
болғандағы пайда болу жылуы
тең 
кал/моль. Осыны 
болғанда
табу керек 
Шешімі.
Ең әуелі жылу сыйымдылақтарды 
дан 
-ға
ауыстырамыз. Реакция түрін жазамыз
.
Содан сон
.
(15)
(15) ті (14) ке қоямыз, болады
+
= 14280 кал/моль.
Есеп 14. Этилді спирттің молярлық
булану жылуы тең 
.
Мұнда t = 15 oC, M = 46 г/моль. Сұйық
спирттің орталанған жылу сыйымдылығы 0,530 кал/(г·град).
Спирттің буының орталанған жылу сыйымдылығы 0,360
кал/(г·град). Мұнда температура аралығы 0≤ t ≤ 78 oC.
Температура t = 60 oC болғанда массасы 500 г. спиртің
булануы үшін кететін жылу мӛлшерін табу керек? Шешімі.
Келесі теңдеуді қолданамыз
.
Бірінші меншікті (массаға қатынасты) булану жылуды табамыз
=
=135,8 кал/моль.
Енді 500 г. спиртті буға айналдыруға қажет жылу мӛлшерін табамыз
500·135,8
= 67910 кал.
Есеп 15. Метилді спирт пайда
болғандағы шығатын жылу эффектіні табу керек 
Келесі реакциялардың жану жылулары белгілі
,
(16)
Дж/кмоль.
Дж/кмоль,
(17)
Дж/кмоль.
Дж/кмоль.
(18)
Сонымен қоса метилді спирт сұйық күйінде жанғанда болады
,
(19)
мұнда
𝑄2,сг =−726,49∙106 Дж/кмоль.
Бізге табу керек 𝑄3 =? Ол келесі реакцияның жылу эффектісі, жылу ӛндіруі
Дж/кмоль.
(20)
Шешімі.
Cонда шешімі болады
𝑄3,обр =𝑄1,сг −𝑄2,сг = −238,7∙ 106 Дж/кмоль.
Яғни, теңдеулердің номерлері бойынша жазғанда
(20) = (16) + (17) – (19).
Есеп 16. Кӛміртегі оттегімен қосылып жану реакциясына түседі. CO пайда болады. Cтандартты жағдайда кӛмір қышқылының қарапайым элементтерден пайда болуының жылу эффектісін табу керек 𝑄1,сг =?
.
(21)
𝑄1,сг - эксперименталды жолмен тікелей анықталмайды.
Шешімі.
Келесі реакциялардың жылу шығаруы белгілі:
Ств +𝑂2 =𝐶𝑂2 +𝑄2,сг , (22)
𝑄2,сг =−393,51∙106 Дж/кмоль
𝐶𝑂+0,5∙𝑂2 =𝐶𝑂2 +𝑄3,сг, (23)
𝑄3,сг =−283,01∙106 Дж/кмоль.
(22)-(23)=(21) алғанда болады
= -110,50
Дж/кмоль.
Есеп 17. Келесі реакцияны қарастырамыз
= СО + 
+ 
.
(24)
Табу керек 
Келесі реакциялардың жылу эффектілері белгілі
.
(25)
-110,50
Дж/кмоль.
Дж/кмоль,
(26)
Дж/кмоль.
Шешімі.
(25)-(26)=(24) .
Сонда
Дж/кмоль.
Реакция номерлері бойынша жазатын болсақ (23) = (21) – (22)
Дж/кмоль.
Жылу мӛлшерінің таңбасы оң (+), яғни реакцияда жылу жұтылады. Таңба минус болғанда – реакцияда жылу сыртқа шығады, ӛндіріледі.
Дж/кмоль.
Яғни осы реакцияда жылу (энергия) жұтылады.
Есеп 18. Келесі реакциядағы
Дж/кмоль,
(27)
Жылу эффектіні табу керек 
Берілгендер, стандартты жағдайда жану жылулары
2𝐶𝑂+𝑂2 =2𝐶𝑂2 +𝑄1,сг , (28)
𝑄1,сг =−283,01·106 Дж/кмоль.
Дж/кмоль,
(29)
𝑄2,сг =−241,84·106 Дж/кмоль.
Шешімі.
Теңдеулерді бір-бірінен аламыз, (28) - (29), болады
𝐶𝑂−𝐻2 =𝐶𝑂2 −𝐻2𝑂г −41,17·106 Дж/кмоль.
Немесе
𝐶𝑂+𝐻2𝑂 =𝐶𝑂2 +𝐻2 −41,17·106 Дж/кмоль.
Соңында жауабы
𝑄𝑝 =−41,17·106 Дж/кмоль.
Есеп 19. 𝐶𝐻4 - метанның 𝐻2 сутегінен және С кӛміртегінен пайда болғандағы реакцияның жылу эффектісін табу керек. Келесі реакцияның қорытынды жылу эффектісін табу керек 𝑄𝑝 =?
С+2𝐻2 =𝐶𝐻4 +𝑄𝑝 . (30)
Шешімі.
Жылу ӛнімдері белгілі келесі реакцияларды қарастырамыз
,
(31)
𝑄1 =−285,84·106 Дж/кмоль.
𝐶+𝑂2 =𝐶𝑂2 +𝑄2 , (32)
𝑄2 =−393,510·106 Дж/кмоль.
𝐶𝐻4 +2𝑂2 =𝐶𝑂2 +2𝐻2𝑂ж +𝑄3, (33)
𝑄3 =−890,34·106 Дж/кмоль.
(31) ді 2 –ге кӛбейтеміз. Сонсон (32) ге қосамыз. Нәтижені (33) –тен аламыз. Сонда болады
𝐶𝐻4 +2𝑂2 −С−𝑂2 −2𝐻2 −𝑂2 =
𝐶𝑂2 +2𝐻2𝑂ж −𝐶𝑂2 −2𝐻2𝑂ж , (34)
𝑄𝑝 =𝑄3 −𝑄2 −𝑄1 =
−890,34·106+393,510·106 +2∙285,84·106= - 74,85·106 Дж/кмоль.
(34) ден (30) шығады.
Яғни p=po =1 атм = const, t=298 oC стандартты
жағдайда реакцияның изобарлы жылу эффектісі тең 
106 Дж/кмоль. Тұрақты кӛлем изохорлы кездегі реакцияның жылу эффектісін келесі формуладан табамыз
.
∆𝑛=1−2=−1. Болады
𝑄𝑉𝑜,образ =− 74,85·106 +8314,4∙298=−72,372·106 Дж/кмоль.
арасында 
айырмашылық ӛте аз.
Сондықтан кӛп жағдайда оларды бірдей, бір біріне тең
деп есептеуге болады.
Есеп 20. Стандартты жағдайда қарапайым заттардан (𝐻2,𝑂2) су және судың буы (пар) пайда болады. Сондағы пайда болу жылу эффектісі тең
Дж/кмоль, 
Дж/кмоль.
Судан бу
пайда болғандағы жылу эффектіні табу
керек 
Теңдеу келесі
.
(35)
Шешімі.
Судың пайда болуының термохимиялық реакциялары
, (36)
.
(37)
(36) тен (37) ні аламыз, болады
. (38)
(38) ден (35) шығады. Осыдан
44,6∙106 Дж/кмоль.
Есеп 21. Ацетиленнің 𝐶2𝐻2,
судың 𝐻2𝑂ж
, кӛмір қышқылды газдың 𝐶𝑂2 пайда болу жылулары
берілген. 
Дж/кмоль. Ацетиленнің пайда
болу реакциясы эндотермиялық.
Ацетилен жанғандағы жылу эффектісін табу керек 
?
Негізгі теңдеу келесі
.
(39)
Шешімі.
Келесі термохимиялық теңдеулерді пайдаланамыз
,
(40)
,
(41)
.
(42)
Теңделерді қосамыз және аламыз: (41)+(42)-(40). Нәтижесінде (39) шығады, және де
Дж/кмоль.
П. 10. Реакциялардың жылу эффектінің
температураға байланысы. Кирхгоф заңы.
Тарау 2, (1-1), (6-1) - (6-3) формулалардан температура бойынша туынды аламыз
,
(1)
.
Осы формулалардағы туындылар жылу сыйымдылықтарды береді
,
(2)
.
- бір мольға
қатысты деген белгі, Дж/(моль·K), Дж/(моль· oC) . Кейде 
таңбаны (символды) жазбайды.
Кӛп жағдайда бір масса бірлігіне қатысты жылу
сыйымдылықты қарастырады Дж/(кг· oC)
, (3)
Оны әдетте кіші әріппен белгілейді. Содан (1) келесі түрде жазылады
,
(4)
.
(5)
Жалпы түрде жазғанда
.
(6)
(1), (4), (5), (6) - да дифференциалда “d”
таңбаның орнына “δ” символы қолдануы тегін емес. Ол (1)
формула бір-біріне ӛте жақын орналасқан, дифференциалды
күйге емес, бір-бірінен әжептәуір алшақ орналасқан,
интегралды кездегі екі, бір-бірінен алшақ жатқан екі күйге
байланысты жазылған математикалық қатынастар деген сӛз,
. Келесі екі шаманы 
,
– изохоралық және
изобаралық реакциялардың температуралық коэффициенттері деп
атайды.
(4) және (5) формулалармен ӛрнектелетін заңдылықты Кирхгоф заңы дейді.
Изохоралық реакцияның температуралық коэффициенті реакцияның пайда болған ӛнімдерінің (жаңа заттардың) изохоралық жылу сыйымдылығынан алғашқы, реакцияға дейінгі заттардың жылу сыйымдылығын алып тастағандағы шамаға тең болады.
Изобаралық реакцияның температуралық коэффициенті реакцияның пайда болған жаңа заттардың изобаралық жылу сыйымдылығынан алғашқы, реакцияға дейінгі заттардың жылу сыйымдылығын алып тастағандағы шамаға тең болады.
Реакцияға қатысушы заттар (элементтер) кӛп болғанда жылу сыйымдылықтар қосылады, теңдеудің сол жағында бір бӛлек, сонсон теңдеудің оң жағында бір бӛлек.
Осы тұжырым, заңдылық Кирхгоф заңы болады.
Кирхгоф заңы интералды түрде
.
(7)
Кӛп жағдайда 𝑇1 =0 деп қарастырады, абсолюттік ноль температурасы. Сол кезде изохоралық V=const және изобаралық P=const жағдайдағы реакциялар үшін болады
,
.
Екеуін біріктіріп жалпы түрде жазғанда болады
.
(8)
𝑄𝑜 - 𝑇1 =0 сәйкес жылулық эффект.
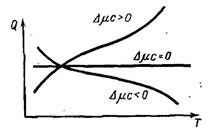
Сурет 1 – Реакцияның жылу эффектісінің температураға және жылу сыйымдылықтың ӛзгерісіне тәуелділігі
(6) кӛрсеткендей 
– функцияның
түрі жылу сыйымдылықтың ӛзгерісіне 
тәуелді,
ӛзгеріс 1-ші суретте кӛрсетілген.
болғанда
реакцияның жылу эффектісі температура ӛскенде – олда ӛседі. 
болғанда реакцияның жылу
эффектісі температура ӛскенде –кемиді. 
болғанда –
тұрақты болады, ӛзгермейді.
П. 11. 
функцияның
түрі.
функцияның түрін
нақтылап ашу үшін 
- функцияның
түрін анықтау керек. Сол үшін келесі реакцияларды қарастырамыз
,
(1)
мұнда B, D, E, G – химиялық заттар белгілері,
элементтер түрлері, 
- мольдар саны.
Реакцияға дейінгі заттардың қорытынды жалпы жылу
сыйымдылығы
.
(2)
Мұнда
,
(3)
–
заттардың жылу сыйымдылығының температураға байланысты тәуелділігі.
Реакциядан кейінгі заттардың қорытынды жалпы жылу сыйымдылығы
.
(4)
Мұнда
,
.
(5)
(1)-(5) - ті (п.10-6) ға қойғанда болады
.
(6)
(6) келесі түрде жазылады
.
(7)
(7) де таңбалар былайша қойылады: (1) дің сол жағындағылар –плюс таңба, ал сол жағындағы мүшелепдің таңбасы – минус.
. (8)
(8) ді интегралдағанда болады
. (9)
Интегралдың константасын 
шектік
шартынан табамыз. Сонда
. (10)
Жаңа белгіілер қабылдаймыз
.
Сонда (10) былай жазылады
.
(11)
Сонымен қоса келесідей де түрде болады
.
(12)
Мұнда
.
(11) де соңғы мүшелерді жазбайды, кӛп жағдайда олар ӛте кіші шама болып отырады.
(11), (12) формулалар бойынша химиялық
процесстердің жылулық эффектілері есептеледі. Екі жағдайда:
P=const, V=const. Қосымша реакцияға дейінгі, реакциядан кейінгі
заттардың жылу сыйымдылығы (реакциядағы температураға
байланысты), және олардың темпераутраға байланысты
ӛзгеретін функция түрі, және абсолюттік нольдік
температурадағы 
- заттардың пайда болу жылу
эффектілері, немесе шекралық шарттағы мәндері белгілі болу
керек. 
- ды белгілі бір температурадағы
реакцияның 
жылулық эффектісі арқылы
анықтауға болады
,
(13)
немесе
.
арқылы белгісіз (басқа бір
температурадағы) 
мәнін анықтауға
болады. Сол үшін екі теңдеуді қатар жазамыз
,
.
Осыдан
.
(14)
(14) тің рӛлі аса маңызды. Ол -эксперименталды жолмен жылу эффектісін анықтауға болмайтын химиялық реакциялардың жылу эффектілерін есептеп табуға болатынын кӛрсетеді.
Ӛзгеретін температура интервалы шамалы болғанда жылу сыйымдылықты орташа мәнімен қабылдауға болады. Сонда
. (15)
Мұнда 
таңба
– бір мольға қатысты дегені, кӛп жағдайда ол
таңбаны жазбайды, 
таңба осы температура
арасындағы орташаланған мән
алынады дегенді белгілейді. (15) тен болады
.
(16)
Осы параграфта қарастырылған нәтижелер проф. Иноземцев Н. В. кітабында сәл ӛзгешелеу жолмен айтылған, ол әдебиет тізімінде кӛрсетілген. Соны қарастырамыз.
Опыт (тәжірибе) кӛрсеткендей,
реакциялардың жылулық эффектісі температураға байланысты
ӛзгереді. Аз мӛлшерде болсадығы. Осыған байланысты
термодинамикалық зерттеулерді Кирхгофф жасаған. Сол бойынша 
- жылулық эффект
температураға байланысты ӛзгереді. Реакция (1) ді қарастырамыз.
Процессті келесі сатыларға бӛліп қарастырамыз:
1) заттар B, D бір
бірімен 
температурада әсерлеседі, 
жылу бӛлінеді.
2) E, G заттарды 
температураға дейін
қыздырамыз. Оған
(17)
жылу мӛлшері кетеді, (4) формуланы қараңыз. Таңбасы минус, себебі жылуды жұтады.
3) 
температурада
E, G – заттар жіктелу (распад, разложение) реакциясына түседі. Сол кезде 
жылу жұтылады. 
,
себебі
.
4) Реакция
аяқталғанда болған заттарды 
температураға
дейін суытымыз. Осы кезде жүйе
(18)
жылу мӛлшерін шығарады, ӛндіреді, (2) ші формуланы қараңыз. 1-4 пункттегі процесстер сурет 1 де кӛрсетілген. Жылулардың қорытынды теңдеуі болады
.
(19)
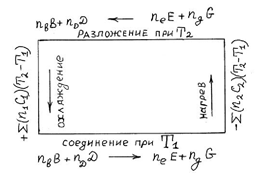
Сурет 1 – Кирхгофф заңына байланысты реакция схемасы.
Немесе
.
(20)
Осыдан
.
(21)
Жалпылағанда (21) ді келесі түрде жазамыз
.
(22)
- формула (1)-дегі реакцияның сол
жағындағы,
содан сон реакцияның оң жағындағы заттардың жылу сыйымдылығының мольдық қосындылары. Осы (22) Кирхгофф заңы. Реакциялардың жылу эффектілерінің температураға байланысты ӛзгерісін кӛрсетеді. Одан арғы нәтижелер (2) – (5) формулалардан бастап, содан кейінгі материалда айтылған.
П. 12. Есеп шығару үлгілері.
Есеп 1. Келесі реакция қарастырылады
.
Мұндағы 
Дж/кмоль.
Табу керек 
, және 
Сонда келесі функциялар белгілі:
,
, Дж/кмоль
, Дж/кмоль
, Дж/кмоль
, Дж/кмоль
Шешімі. 
белгілі
формулалар бойынша 
- коэффициенттерді
табамыз. Сонда
;
;
.
(п. 11-12) формула бойынша болады
.
Стандартты жағдайда 
белгілі.
Осыдан 
анықтаймыз
Дж/кмоль.
Осыдан болады
.
Температура T=1000 K болғанда нәтиже болады
Дж/кмоль.
Есеп
2. Келесі реакцияның 
стандартты
жағдайдағы жылу эффектісі тең 
Дж/кмоль.
Табу керек 
=? , яғни температураға
байланысты жалпы функция ретінде табу керек. Және табу керек 
=? Жылу сыйымдылықтардың
температураға байланысты ӛзгеретін функциялары
белгі:
Дж/(кмоль·K) ,
Дж/(кмоль·K) , 
Дж/(кмоль·K) .
Шешімі.
- формуласы белгілі
деп, коэффициенттер 
- табамыз. Сонда
;
;
.
(11-12) формула бойынша болады
.
Осыдан 
табамыз. Сол
үшін стандартты жағдайдағы 
мәнін
пайдаланамыз.
Дж/кмоль.
Соңында болады
.
Температура 
болғанда
нәтиже болады 
Дж/кмоль.
Есеп 3. Сутегі жанады. Жану реакцияның
жылулық эффектінің температураға байланысын табу керек 
Пайда болған бу
конденсацияланбайды. Т=800 K дегі жылулық эффектіні табу керек
Негізгі теңдеу келесі
.
Теңдеуге кіретін
заттарға кестеден 
және жылу сыйымдылық 
мәндерін табамыз
,
,
.
Стехиометриялық коэффициенттерді ескере отырып,
- мәндерін табамыз
,
,
.
Тәуелділік формуласы болады
/T.
арқылы осыдан 
табамыз
.
Соңында болады
.
Температура Т=800 K болғанда 
Дж/кмоль.
Тарау 4. Реакция бағытын болжау.
П. 1. Тепе теңдік константа және диссоциация.
Күрделі химиялық заттар температура ӛскенде ыдырайды, яғни құрамды элементтерге бӛлінеді, тарайды. Осы процессті диссоциация дейді. Диссоциялық реакциялар эндотермиялық болады, яғни онда жылу жұтылады, жылу жоғалады. Жүйенің жылуы кемиді. Мысал ретінде су буының, кӛмір қышқылының, азот қышқылдарының ыдырау реакцияларын қарастыруға болады
2𝐻2𝑂 ⇄2𝐻2 +𝑂2 , (1)
2𝐶𝑂2 ⇄2𝐶𝑂+𝑂2 , (2)
2𝑁𝑂2 ⇄2𝑁𝑂+𝑂2 , (3)
𝑁2𝑂4 ⇄2𝑁𝑂2, (4)
2𝑆𝑂3 ⇄2𝑆𝑂2 +𝑂2 , (5)
2𝑁𝐻3 ⇄𝑁2 +3𝐻2 , (6) т.б.
Диссоциация кӛрсеткіші 𝛼 сан бойынша қанша молекула (немесе атом) ыдырап кеткенін кӛрсетеді. Процентке айналдырады. Немесе ыдырап кеткен (тарап кеткен) молекулалардың мольдық мӛлшерін процент бойынша кӛрсетеді.
Реакция константасын диссоциация кӛрсеткішімен байланыстырған кӛп жағдайда практикалық есептерді шығарғанда пайдалы болады 𝐾 =𝑓(𝛼). Осы функция сан алуан түрлі реакцияларға да әртүрлі болып отырады. Қарапайым кейсібір реакцияларға белгілі болғанда, басқа күрделі реакцияларға да соған қарап табуға болады. От простого к сложному деген логикамен. Осы функцияға негізгі әсер етуші қысыммен кӛлем.
Тепе теңдік күйге келетін реакцияларды жалпы үш түрге бӛлеміз: 1) моль саны азаяды ∆𝑛<0 , 2) моль саны кӛбейеді ∆𝑛 >0, 3) моль саны ӛзгермейді ∆𝑛 =0. Осы жағдайларды қарастырайық.
1) біріншіде ∆𝑛<0 жағдайды қарастырамыз. Формула (1) ге сәйкес реакция константасы
. (7)
Температура және қысым
тұрақты (фиксированный) болғанда диссоциация кӛрсеткіші
болсын, P=const, T=const. (1)
формулаға сәйкес әрбір 
мольдан бір
бӛлік 
, екінші бӛлік 
болып
шығады. Тепе теңдік күй кезінде алғашқыда бір
моль болған заттан 
бӛлігі қалады. Ал 2 моль
заттан 
бӛлігі қалады.
Шығысында 2 моль 
, 1 моль 
болады.
Сонда тепе теңдік кезде
+
+
.
- - - - - - - - - - - - - - - - - - - - - - -
Барлығы: (200+
Ескереміз
,
сонда парциалдық қысымдар болады
,
,
.
Тепе теңдік кездегі концентрацияларды табамыз
,
(8)
,
(9)
. (10)
(4) ке (8)-(10) ні қоямыз, сонда болады
,
(11) мұнда
,
.
Соңында (11) мына түрде жазылады
.
(12)
Енді 
табамыз
.
(13)
Осы реакцияға болады
. (14)
(14) ді (13) ға қойғанда, (11) ді ескере отырып болады
.
Осыдан шығады
.
(15)
(15) ге (12) ды қойғанда болады
.
(1)-ші реакцияны енді V=const,
T=const жағдайында қарастырайық. 
ның
бір мольдан ыдыраған, тараған мӛлшерді 
деп
белгілейік. Сонда тепе теңдік күй кезінде 2 моль 
судан
ыдыста 2(1-α) моль бу болады, 2α моль 
су тегі
молекeлалары, 
моль оттегі 
молекулалары
пайда болады. Тепе теңдік кезіндегі концентрация болады
,
(16)
, (17)
.
(18)
(16)-(18) ті (4) ке қойғанда болады
.
(19)
реакция үшін
нәтижелер тура осындай болады. Яғни (1) мен (2) бірдей. 
мен 
диссоциялары ішкі
жану қозғалтқыштарында үлкен роль атқарады.
Сондықтан осы нәтижелер практикада маңызды болып табылады. 
немесе 
мәндері
белгілі болғанда диссоциация 
да белгілі болады.
Яғни жоғалған немесе ӛндірілген жылу мӛлшерлерін
есептеуге болады. Жоғарыда айтылғандай екі жағдай орында болу
керек: 1) V,T = const; 2) P,T= const. 
болғанда
қысым
P ӛскенде диссоциация 
керісінше
азаяды. Ал кӛлемнің ӛсуі диссоцияны да ӛсіреді,
кӛбейтеді.
Осы айтылған ережелерге (1)-(6) реакциялар бағынады.
2) екіншіде 
жағдайды
алайық. Газ генераторларында жиі болатын келесі реакцияны
қарастырамыз
.
(20)
Осы кезде 
. Реакция константасы
.
- 1 моль CO ның
қаншама бӛлігі ыдырады, бӛлініп кетті – соны кӛрсететін
шама, процент бойынша. Сонда тепе теңдік күй орнағанда 
ның мӛлшері 2·(100 -
) болады. 
-
нің пайда болған мӛлшері 
болады.
Кӛміртегі С қатты зат күйінде,
фазада, сондықтан оны 
ке еңгізбейміз.
Сонымен, тепе теңдік кезде болады
СО = 2·(100 -
) ,
+
= 
.
- - - - - - - - - -- - - - -
- - - - - - - - - - - - -
-
Барлығы: (200 – 
)
P,Т = const шартында болады
;
.
,
немесе
.
(21)
Келесі формуланы пайдаланамыз
.
Осыдан
.
(22)
(21), (22) – P,T = const жағдайдағы есептің шешімі, жауабы.
Реакция (20) ны енді V,T = const жағдайда
қарастырайық. Бұл кезде 
- CO ның
ыдырап, тарап кеткен моль санының проценттік кӛрсеткіші.
Тепе теңдік орнаған кездегі концентрациялар болады
,
.
Сонда тепе теңдік контантасы болады
.
(23)
(22) формула кӛрсеткендей, T=const кезде, P -
ның ӛсуі 
ның ӛсуін тудырады. (23)
кӛрсеткендей T=const кезде, V-ның ӛсуі 
ның
азаюына келтіреді. Осы қорытынды 
болатын барлық
реакцияларға орындалады.
3) Енді 
жағдайды
қарастырамыз. Осыған келесі реакциялар сәйкес болады
,
(24)
,
(25)
.
(26)
Жоғарыдағыдай, α – ыдырау, бӛліну дәрежесінің кӛрсеткіші.
(24) реакцияға болады
.
(25) реакцияға болады
.
(26) реакцияға болады
.
болған кезде және
температура тұрақты болғанда қысымның және
кӛлемнің ӛзгеруі тепе теңдік күйді
бұзбайды, ӛзгертпейді. Тарау 3 параграф 3 тегі есептерде 
орнына X деп жазылған.
П. 2. Тепе теңдік константаны эксперименталды түрде анықтау.
Тепе теңдік константаны 
анықтау
және диссоциация дәрежесі 
ны анықтау
мәселелері – екеуі бір-бірімен тығыз байланысты. Соларды
қарастырамыз. Деваль тәжірибесі.
Онда 1 суреттегі тәжірибелік қондырғыда эксперименталды ӛлшеулер жасалған.
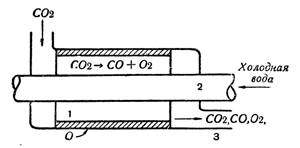
Сурет 1 – Девальдың тәжірибелік қондырғысы.
газы қыздырылған 1
камераға кіреді. Сонда ол диссоциацияға
түседі
.
(1)
Тепе теңдік күй орнайды. Түтік 2
ден суық су ӛтеді, салқындатады, ассоцияны (қайтадан
бірігуді) тежейді, болдырмайды. Шығатын түтік 3 те диссоциация
дәрежесі 
–ны анықтайды.
Сонда тепе теңдік константасы келесі формуламен анықталады
.
(2)
Нерст тәжірибесі.
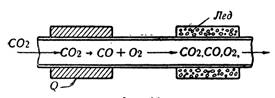
Сурет 2 – Нернст тәжірибесі.
Мұнда да реакция (1) – ге сәйкес. 
жүретін түтік мыстан
жасалған. Түтіктің бірінші сол жақтағы
бӛлігі белгілі бір температураға дейін қыздырылады. Сонда
ыдырау реакциясы жүре бастайды. Түтіктің оң жағында
суу, салқындау процесі жүреді. Осы салқындаған
жақта 
–ны анықтайды, (2) формула
бойынша.
Левенштейн тәжірибесі.
Левенштейн тәжірибесі Нерст лабораториясында жүргізілген. Платина >600 оС жоғары қызғанда сутегі молекуласын ӛткізеді, басқа молекулаларды ӛткізбейді. Осыны Левенштейн тәжірибесінде пайдаланады.
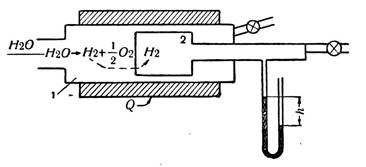
Сурет 3 – Левенштейн тәжірибесі.
Судың буы 1-ші қыздырылған камераға (түтікке) келеді. Онда белгілі бір температурада тепе-теңдік күй орнайды. Реакция келесі
2𝐻2𝑂 →2𝐻2 +𝑂2.
Сутегі 2-ші камераға кіріп ондағы қысымды ӛсіреді. Сутегінің парциалды қысымы арқылы оның мӛлшері анқыталады. Содан 𝛼–ны анықтайды. 𝐾𝑃 сол (2) формуламен есептеледі.
Осы айтылғандарды бірнеше есеп мысалдарымен бекітейік.
Есеп 1.
Келесі реакцияны қарастырамыз
𝐶𝑂+𝐻2𝑂 ⇄𝐶𝑂2 +𝐻2 . (3)
Тепе теңдік орнау кезіндегі қоспаның проценттік құрамын табу керек? Алғашқы құрамы мынандай:
𝑟𝐶𝑂 =10% , 𝑟𝐻2𝑂 =15% , 𝑟𝐻2 =1% , 𝑟𝐶𝑂2 =12% , 𝑟𝑁2 =62% .
Және температура 𝑡 =986 𝑜𝐶 болғанда 𝐾𝑃 =1,60 . Шешімі.
Осы есепті диссоцияция дәрежесі 𝛼 арқылы шешейік. 𝛼–кӛлем бойынша немесе моль саны бойынша тарап (ыдырап) кеткен зат мӛлшерінің проценттік кӛрсеткіші. Сонда тепе теңдік орнаған кезде болады
𝐶𝑂2 =𝑟𝐶𝑂2 −𝛼 ,
𝐻2 =𝑟𝐻2 −𝛼 ,
(4)
𝐶𝑂 =𝑟𝐶𝑂
+𝛼, 
,
.
- - - - - - - - - - - - - - - - - - - -
100%
. Осыдан
,
,
(5)
,
.
Концентрация үшін
.
Сонда
,
,
(6)
,
.
Мұнда 
, содан 
.
.
Мәндерін қойғанда болады
.
Болады
.
Осыдан
, 
. Бірінші оң
мәнді шешімді қарастырмаймыз, ол физикалық шартқа
келмейді. Соңында тепе теңдік күйде болады
;
;
;
;
.
теріс сан болғандықтан
реакция солдан оңға қарай жүреді.
Яғни 
пайда болып,
кӛбейіп жатады.
Есеп 2.
Дизель цилиндрінде жану процесінің соңғы кезеңі қарастырылады.
газының диссоциация дәрежесі
ны табу керек? Осы кӛмір
қышқылы газдың пациалдық
қысымы 
, температура
Т=1980 К, тепе теңдік константа 
.
Шешімі.
Қарастырылатын реакция
.
Тепе теңдік константасы тең
.
ӛте кіші шама болғанда 
, 
.
Сонда
.
Осыдан
.
Есеп 3.
Дизель цилиндрінде жану процесінің соңғы кезеңі қарастырылады.
газының диссоциация дәрежесі
ны табу керек? Осы кӛмір
қышқылы газдың пациалдық
қысымы 
, температура
Т=1980 К, тепе теңдік константа 
.
Шешімі.
Қарастырылатын реакция
.
Тепе теңдік константасы тең
.
ӛте кіші шама болғанда 
, 
.
Сонда
.
Осыдан
.
Есеп 4.
Ыдыста бастапқы моментте 10 моль 
болды. Тепе теңдік константа
, температура 
. Тепе
теңдік кезіндегі
қоспаның құрамын анықтау керек? Шешімі.
Реакция келесі
. Тепеп теңдік константа
тең
.
Осыдан
.
Есептегенде
.
Соңында тепе теңдік кезінде диссоциаланады (бӛлінеді)
0,22∙10=2,2 моль HJ.
Ал қоспада қалады 10-2,2 = 7,8 моль HJ. Және де пайда болады:
моль.
моль.
П. 3. Реакцияның атқаратын максималды жұмысы және реакция константасы.
Химиялық реакция максималды (ең
үлкен, мүмкін деңгейі) жұмыс жасайды. Осы жұмыс
элементтердің химиялық сродствосы болады. Реакция
термодинамикалық қайтарымды болғанда ғана жасалатын
жұмыс максималды болады. Максималды жұмыс тепе теңдік
константалары арқылы анықталады 𝐴𝑚𝑎𝑥
=𝑓(𝐾𝑃) . Осы байланысты
табудың әртүрлі жолдары бар. Вант-Гофф анықтаған
жолды қарастырамыз. Ол ӛзінің кӛрнектілігімен
ерекшеленеді. 2𝐻2𝑂
⇄2𝐻2 +𝑂2 реакцияға
байланысты айтамыз. A, B, D үш ыдыс берілген, сурет 1. Сол ыдыстарда 𝐻2 , 𝑂2 , 𝐻2𝑂
газдар бар, температура тұрақты. Заттардың мольдық-
кӛлемдік (моль/м3) концентрациясын 𝐶𝐻2𝑂
, 𝐶𝐻2,
𝐶𝑂2
деп белгілейміз. Ыдыстар кӛлемі жеткілікті үлкен, моль сандары
кӛп, сондықтан бір-екі моль азайып не қосылып жатса – жалпы
жағдайға әсер етпейді. Сондықтан опыт (тәжірибе)
кезінде 𝐶𝐻2𝑂
, 𝐶𝐻2,
𝐶𝑂2
және парциалдық қысымдар 𝑃𝐻2𝑂
, 𝑃𝐻2,
𝑃𝑂2
тұрақты болады, ӛзгермейді. Сонымен қоса E жәшігі
бар, оны бірқалыпты, біртекті (равновесный) күйді ұстайтын
ыдыс дейді. Осы жәшікте үш газ бірдей 𝐻2 , 𝑂2 , 𝐻2𝑂 . Оларда
химиялық реакция жүрмейді, яғни бірқалыпты күйде.
Осы E ыдыстағы бірқалыпты күйдегі концентрацияларды
және қысымдарды 
, 
, 
және парциалдық
қысымдар 
Және де 
,
, 
,
, 
, яғни E
ыдыстағы мәндер басқа ыдыстағы мәндерден кіші. А,
B, D –ыдыстардағы газдар орнықты бірқалыпты күйде емес,
неравновесное состояние.
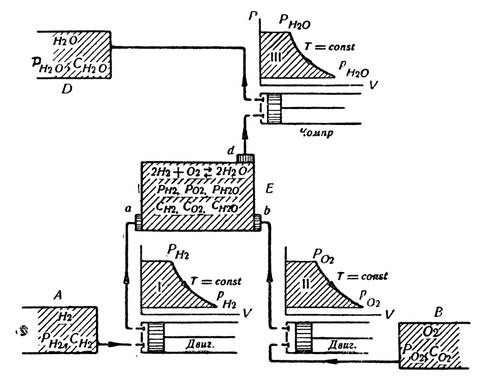
Сурет 1 – Вант-Гофф нәтижесін дәлелдеуге схема.
Е ыдыста үш перегородка - тежеуші
қабырға бар. Әрбір перегородка тек бір ғана газды
ӛткізеді. Перегородка а – тек сутегін ӛткізеді, b – тек оттегін
ғана ӛткізеді, ал перегородка с – тек судың буын ғана
ӛткізеді. Поршені бар үш цилиндрлар газдарды A, B, D ыдыстардан –
E ыдысына қарай және кері бағытта ығыстырады (качает).
Мақсат – екі моль 
және бір моль 
ден
– екі моль су буын 
шығару. Процесс қайтарымды
болу керек, және соңында максималды жұмыс – 
шығару
керек . 
+ 
→ 
. Процесс жүріп жатқанда
мұнда температура және қысым тұрақты. Келесі
операциялар жасалады. 1) А ыдыстан 2 моль 
аламыз,
оның қысымын 
, Концентрация- сын
қалпына жеткіземіз, сонсон E
ыдысқа еңгіземіз. Бастапқы D ыдыстағы мәндері 
, 
болған. Осы
суретте 1-ші цикл. Жасалған жұмыс болады
,
Екі мольдің жұмысы болады
.
(1)
формуласы арқылы (1) ді жазамыз
.
(2)
2)
B ыдыстан 1 моль 
аламыз, оның
қысымын 
, Концентрация- сын
қалпына жеткіземіз, сонсон E
ыдысқа еңгіземіз. Бастапқы B ыдыстағы мәндері 
, 
болған. 1 –ші
суретте 2-ші цикл. Жасалған жұмыс болады
,
Концентрация арқылы жазғанда болады
.
(3)
3)
E ыдыстан 2 моль 
аламыз да D ыдысына
кіргіземіз. Сонда оның қысымы 
, концентрациясы 
дан басталып, сонсон D ыдысқа
кіргенде мәндері 
, 
болады. 1 –ші
суретте 3-ші цикл.
Жасалған жұмыс теріс мәнді болады
.
(4)
E ыдыстан D ға қанша 
кетсе, соншама мӛлшерде Е ыдыста
жаңадан 
пайда болып жатады: 
.
Сондықтан Е ыдыстағы бірқалыпты тепе-теңдік күй
сақталады, бұзылмайды.
Осы 3 қадам жасалғанда нәтижесінде келесі реакция
толық, тұйықталған, қайтарымды циклмен жүріп ӛтеді, мұнда V,T = const.
Соңында (2) - (4) негізінде қорытынды жұмыс келесі түрде жазылады
,
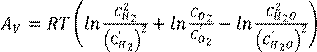немесе максималды жұмыс тең болады
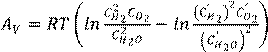. (5)
Алдында айтылғандар бойынша
.
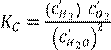(6)
(6) ны (5) ке қойғанда максималды жұмыстың формуласы болады
.
(7)
(7) формула қорытылды массаның әрекеттесу заңы негізінде, закон действующих масс. Бұл жолда химиялық реакцияның жылдамдығы ұғымы пайдаланды.
Осы формуланы қорытып шығарудың
екінші жолы бар. Ол – термодинамикалық жол, ӛзгеше жол. Бұл
екінші жолда 
, 
, 
-
күйден басқа, тағы да бір
ӛзгеше күй болды делінеді. Сонда, екінші күйде параметрлер
келесі болады: 
. Мұндай ӛзгеше күйге
келу үшін E ыдыста қысымды ӛзгертеді, ол 
болады.
E ыдыстағы бұрынғы кездегі жалпы (общий) қысым 
, бұл бірінші кездегі қысым.
Екінші күйдегі де параметрлер бірқалыпты тұрақты
болады. Екінші кездегі
газдардың парциалдық қысымдары
келесі 
. А, В, D ыдыстардағы
параметрлерді сол бұрынғыдай қылып сақтаймыз.
(5)-(7) формулаларды қорытқандағы амалдарды жасағанда
болады
.
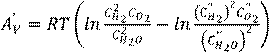(8)
(7) мен (8) екеуі – екі бӛлек процесске
арналған. Дегенмен екеуінде де температура бірдей, тұрақты.
Және де бастапқы физикалық параметрлер бірдей: 
, 
, 
.
Қайтарымды процесс біткенде соңғы күйдегі параметрлер
де бірдей. Сондықтан 
,
(7) = (8). Осы тұжырым Мутье теоремасы деп аталады.
.
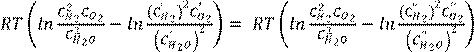Осыдан
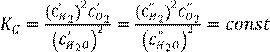. (9)
(9) – маңызды нәтиже, ол тепе теңдік константаның толық анықтамасы, сипаттамасы болып табылады.
П. 4. Жалпы түрде жазылған реакциялар.
Химиялық реакцияларды жалпы түрже жазайық
.
Сонда болады
.
(1)
Немесе
,
(2)
мұнда
.
Парциалдық концентрация 
орнына парциалдық қысымды 
қарастыруға болады. Формула
келесі 
. Сонда болады
,
(3)
мұнда
.
(1) - (3) тен шығады
,
,
. (4)
(4) шығады
.
(5)
(2) мен (5) формула ӛте маңызды болып табылады. Олар V,T = const болғанда максималды жұмыспен реакция константасы арқылы байланысты орнатады. Біртекті күйдегі жалпы қысымды кіші p мен белгілейді
.
Біртекті емес, қалыптаспаған күйдегі жалпы қысымды үлкен P мен белгілейді (неравесное состояние)
.
Химиялық реакцияларда P,T=const жағдайы жиі кездеседі. Мұнда P – қоспаның жалпы қысымы. Осындай жағдайға (2) , (5) келесі түрде жазылады
,
(6)
.
(7)
(2) , (5) , (6), (7) – жазылуы бірдей. Алайда, 
. Себебі екі түрлі жағдайда
парциалдық қысымдар әртүрлі болады, біреуінде
қысым тұрақты (кӛлем ӛзгере береді), екіншіде
кӛлем тұрақты (парциалдық қысымдар ӛзгере
береді). Жұмыстағы индекстерді ескермесек, жалпы жағдайда
жазамыз
A 
,
(8)
A
. (9)
V, P – ға байланысты айырмашылықтарды ескермеген жағдайда
(8) , (9) формулаларды химиялық реакңциялардың изотермалары деп атайды.
Кейбір кезде есептеулерді қарапайымдату,
салыстыруды жеңілдету үшін бастапқы парциалдық
концентрацияны 
, бастапқы парциалдық
қысымды 
деп алады. Сонда максималды жұмыс
тең болады
,
(10)
.
(11)
, сондықтан 
шығады.
Сондықтан практикада кӛптеген кестелерді
құрастырғанда қай физикалық жағдайда
болғаны V,T=const немесе P,T=const – ерекше айтылып отыру керек. Газ
ба, әлде қатты дене ме? – ол да айтылып отыру керек.
Мысал ретінде келесі гетерогендік реакцияны қарастырайық
.
Барлық компоненталар газды
болғанда ыдыстың (резервуар) ішіндегі заттардың
мӛлшері тепе теңдік күйге сәйкес болады. Дегенмен
компонентаның біреуі қатты дене болғанда, оның
мӛлшері сол денеден шыққан буға (парға)
әсері болмайды. Сондықтан қатты дененің мӛлшері
артығымен, кез келген мӛлшерде бола береді. Ал газды
құрамдағы заттар (
) – тепе теңдік
константаға сәйкес болады. Сондықтан кӛміртегін
біртекті күйдегі ыдысқа тасымалдауға байланысты жұмыс
болмайды. 
- байланысты ыдысқа тасымалдау
жұмыстары болады, сақталады.
Ол жұмысты компрессор жасайды.
Бір моль оттегін ыдысқа кіргізe жұмысы тең болады
.
Ол оң таңбалы жұмыс. Екі моль СО ны ыдысқа еңгізу жұмысы тең
.
Осы жұмыс минус теріс мәнді. Осы екі жұмыстың қосындысы максималды жұмыс болады.
,
немесе
.
(12)
(12) ды келесі түрде жазамыз
,
(13)
мұнда
.
Мұнда штрихпен жазылғандар – уақыт ӛткенде тепе теңдік орнаған біртекті күйге жатады. Ал штрихсыз жазылғандар -бастапқы уақыттағы тепе теңдік орнамаған біртекті емес, ӛзгермелі күйге жатады. Жалпылап жазғандағы жұмыс болады
.
(14)
(14) жазылуы бойынша газдық реакцияларға арналған (6), (8) бен бірдей. Мұндай формула ұқсастығын, бірлестігін гетерогендік реакцияларды қарастырғанда қатты денелерге, қатты немесе сұйық фазаға байланысты концентрацияны жазбағандықтан ғана қол жеткіздік.
П. 5. Реакция бағыты. Тепе теңдік шарты.
Бастапқы концентрациялар 
тепе
теңдік кездегі концентрациялар 
тан
алшақтығы неғұрлым үлкен болса,
соғүрлым максималды жұмыс үлкен болады және
химиялық сродство үлкен болады. Егер 
болса,
реакция солдан оңға қарай жүреді, A, B айналады C, D
ға. Егер 
болса реакция оңнан солға
қарай жүреді. C, D айналады A мен B-ға.
Соңында 
болғанда реакция динамикалық
тепе теңдікте болады. Реакция қаншама солдан оңға
ӛтсе, соншама оңнан солға қарай ӛтеді. Екі
жақтан зат мӛлшері тұрақты болады, не азаймайды, не
кӛбеймейді. Осы кезде
,
.
Осыдан шығады. Бастапқы концентрацияларды және қысымдарды тепе теңдік күйге сәйкес қылып алсақ, химиялық реакция ешқандай да жұмыс жасамайды.
Осы тақырыпқа есеп шығару үлгісі.
Есеп. Реакция келесі 
.
Температура t = 444 oC, тепе теңдік константа 
Осы
температурадағы реакция бағытын анықтаңыздар.
Бастапқы концентрациялар келесі үш жағдаға , үш
шартқа байланысты берілген:
;
(1)
;
(2)
; (3)
Осы реакцияға байланысты изотерма теңдеуі болады
.
(4)
(1)-(3) бастапқы шарттарды (4) ке қоямыз, сонда келесі үш түрлі нәтиже шығады:
1.
.
, сондықтан
реакция солдан оңға қарай жүреді. Яғни 
пайда болу бағытында жүреді.
.
, сондықтан
реакция оңнан солға қарай жүреді. Яғни 
пайда болу, кӛбею бағытында
жүреді.
.
Осы кезде жүйе динамикалық тепе теңдікте болады. Реакцияда заттардың концентрациялары ӛзгермейді. Оң жақ пен сол жақтағы заттар тепе теңдік күйде болады.
П. 6. Тепе теңдік константаның температураға байланысы.
Химиялық тепе теңдік және тепе теңдік константа температураға байланысты ӛзгереді. Осы байланысты табу үшін осының алдында табылған шешімдерді қарастырайық. V=const болғанда
,
(1)
.
(2)
Мұнда 
- реакцияның
максималды жұмысы, 
- реакцияның жылулық
эффектісі, 
– реакция константасы.
(1) ді T бойынша туындылайық:
.
(3)
(3) ті қоямыз (2) ге:
, (4)
. (5)
(5) тен болады
.
(6)
(6) дан шығады
,
(7)
.
(8)
Осы теңдеу V=const шартына сәйкес. Сондықтан химиялық реакцияның изохорасы деп аталады.
Енді жүйені P=const жағдайында қарастырайық. Осы жағдайда болады
,
(9)
.
(10)
Мұнда 
- реакцияның
максималды жұмысы, кӛлемге байланысты жұмысты алып
тастағанда, 
- реакцияның жылулық
эффектісі P=const болғанда, 
– реакция
константасы.
(9) дан T бойынша туынды аламыз
.
(11)
(11) ді (10) ға қоямыз
, (12)
. (13)
(13) ті мына түрде жазамыз
.
(14)
(14) тен шығады
,
(15)
.
(16)
(15), (16) теңдеу P=const шартына сәйкес. Сондықтан химиялық реакцияның изобарасы деп аталады.
(7), (8), (15), (16) теңдеулерде P,V индекстерін жазбауға болады, жоғарыда айтылған. Сонда болады
,
(17)
K
.
(18)
Техникалық жүйеде R=2 кал/К. Сонда
.
(19)
(17)-(19) маңызды қорытынды шығады:
1)
Q>0 болғанда, 
болады. Яғни
экзотермиялық реакцияларда температура ӛскенде тепе теңдік
константа да ӛседі. Константаның ӛсуі бастапқы
заттардың концентрациясы немесесе парциалдық қысымдары
ӛседі деген сӛз. Ӛйткені K формулада, бастапқы
заттардың концентра- циясы формулада алымында тұрады. Осыдан
маңызды қорытынды шығады: экзотермиялық реакцияларда
реакция продуктісі , шығардағы ӛнімі кӛптеу болу
үшін температура мәні тӛмендеу болғаны дұрыс.
Тепе теңдік күй сол жаққа жылжиды.
2)
Q<0 болғанда, 
болады. Яғни
эндотермиялық реакцияларда температура ӛскенде тепе теңдік
константа тӛмендейді, кішірейеді. Константаның кішіреюі
бастапқы заттардың концентрациясы нмесесе парциалдық
қысымдары да кішірейеді деген сӛз. Ӛйткені K формулада,
бастапқы заттардың концентра циясы формулада алымында тұрады.
Осыдан маңызды қорытынды шығады: эндотермиялық
реакцияларда реакция продуктісі , шығардағы ӛнімі максималды
кӛптеу болу үшін температура мәні жоғары, үлкен
болғаны дұрыс. Тепе теңдік күй оң
жаққа жылжиды. K мәні ӛскенді сол жаққа
ауыстық, ал кішірейгені – оң жаққа ауыстық
дейміз, тепе теңдік күй бойынша. Реакция формуласында
“
” таңбаның сол
жағымен оң жағы туралы айтылады.
П. 7. Есептейтін теңдеулер. Есеп мысалы.
П. 6 дағы (6-19) теңдеуді қарастырайық. Осы теңдеуді интегралдағанда болады
.
(1)
Бұл (6-19) дың жалпы шешімі. Әзірше интегралдық константа белгісіз. Оны Нернстің теоремасы негізінде анықтайды. Кейінде айтамыз. Интегралдық константа С анықталмағанша (1) ді пайдалана алмаймыз.
(6-19) ды екі температура аралығында интегралдаймыз, сонда болады
.
(2)
Жуықтағанда 
аралығында
шамамен тұрақты дей
отырып оны интегралдың сыртына шығарамыз, сонда
.
(3)
Формула (3) техникада кең
қолданылады. Осы формула 
температурада 
белгілі
боғанда, екінші бір 
температурадағы белгісіз 
мәнін есептеуге мүмкіндік
береді. Қосымша 
мәні белгілі болуы керек.
Температура айырмасы 
үлкен шама болмау керек. Себебі 
үлкен интервалда ӛзгергенде,
сол арада 
тұрақты болмайды, ол да
ӛзгеретін бір функция болады. Жәй ғана интегралдың
сыртына шығара салуға болмайды.
Осы тақырыпқа есеп шығару үлгілерін қарастырамыз.
Есеп 1.
Ыдыста 1 моль CO және 1
моль 
бар. 
= 800 K
болғанда тепе теңдік күйге сәйкес газдардың
құрамын табу керек. Бастапқы күйде 
болғандағы
Реакцияның жылулық эффектісі
тең
.
Екінші жағдайда,
яғни 
= 800 K кездегі реакция түскен СО
немесе 
мӛлшерін (құрамды
бӛлік түрінде) х – деп белгілейік. Сондықтан
осы тепе теңдік күйде болады:
CO = 1-X моль,
= 1-X моль, 
X моль, 
X моль.
Сонда тепе теңдік константа тең болады
.
(4)
(3) формула бойынша екінші жағдайға сәйкес
.
(5)
(5) формулаға мәндерді қоямыз
.
Осыдан шығады
.
Енді (4) ші формуланы пайдаланамыз
.
Сонда болады X=0,72. Осы X ке сәйкес,
яғни 
= 800 K сәйкес сол кездегі
қоспаның құрамы келесі болады
CO = 1- 0,72 = 0,28 моль,
=
1- 0,72 = 0,28 моль,
0,72
моль,
0,72
моль.
Есеп 2.
Келесі реакцияның жылулық эффектісін табу керек Q=?:
.
Температура ӛзгереді аралықта 
. Және белгілі
,
мұнда 
.
,
мұнда 
.
Тарау 5. Гальваникалық элементтер теориясы
П.1. Мыс, қола, алтын элементтері.
Осы топтағы подгруппадағы металлдардың түcі болады: мыс қызғылтым, күміс – ақ, алтын – сары-қызғылтым. Олар – иіледі, созылады, майысады (ковкие и пластичные). Мысалға, илемдеумен (прокаткамен) алтынның жұқа беттерін 0,0002 мм, ал 1 г. алтыннан 3420 м ұзындықты сым шығаруға болады. Электр және жылу ӛткізгіштігі бойынша орындары: күміс, мыс, алтын.
Алтын азот қышқылында ерімейді. Ол тек “царская водка” деп аталған қоспада ериді. Царская водка құрамы: концентрациясы жоғары азот қышқылы және концентрациясы жоғары тұзды, хлорды қышқылы. Олардың концентрациялық қатынасы 1:3. Реакция түрі
Азот қышқылы металлдарға әсер еткенде, қоспалар пайда болады, сонда азоттың қышқылдану дәрежесі кіші шама болады. Азот қышқылы химия ӛндірісінің ең кӛп мӛлшерде шығатын ӛнімі болып табылады.
Құм мен ұсақталған кварцтық породадан алтын сумен жуылып шайылады. Немесе алтынды ерітетін сұйықтармен қоқыстардан бӛлінеді. Ең жиі болып Натрийдің цианиді қолданады NaCN. Келесі реакция жүреді
.
Алынған ерітіндіден алтынды цинкімен ығыстырып шығарады
Алтын ерітінді түбіне түседі. Цинкіден ажырату үшін аз ерітілген күкірт қышқылымен ӛңдейді, сумен жуады, кептіреді. Одан әрі – күмістен ажырату керек. Сол үшін материалды концентарциясы кӛп мӛлшерде ерітілген күкірт қышқылымен ӛңдейді. Немесе екінші жол – электролизбен ажыратады, бӛліп алып сонсон жинайды.
П. 2. Коррозияның химиялық негіздері.
Химиялық элементтердің электрлік кернеулер қатарында темір Fe сутегі Н2 ге дейін орналасқан. Сондықтан ол су тегі Н атомын судан ығыстырады.
𝐹𝑒+2𝐻+ =𝐹𝑒2+ + 𝐻2 ↑
Суда ерітілген оттегі болады. Ол екі валентті теміріді үш валенттікке дейін қышқылдатады. Темірдің коррозиясының қорытынды реакциясы келесі теңдеумен сипатталады
4𝐹𝑒+ 𝐻2𝑂+3𝑂2 =4𝐹𝑒𝑂(𝑂𝐻). (1)
Үш валентті темірдің оксид-гидрооксиді 𝐹𝑒𝑂(𝑂𝐻) темірдің тотыққан және шіріген бӛлігін құрайды. Ржавчина деп аталады.
Темірдің коррозиясымен күресудің әртүрлі жолдары бар. Соның бірі – коррозияға тӛзімді материал шығару. Мысалға темірге 18% Cr, 9% Ni, және 1 % Ti қосады. Қалғаны 72% - Fe.
Реті келген жағдайда темірден жасалған материалдың орнына металлдық емес – графиттік, пластмассалық, т.б. материалдар қолданылады.
Алайда, тотығуға тӛзімді (нержавеющие) материалдар қымбат болады, ал басқадай, металлдық емес материалдармен алмастырудың реті келе бермейді. Сондықтан, темірден жасалған ӛнімді коррозиядан қорғау (защита) – бірінші, тиімді жол болады. Коррозиядан қорғаудың тиімді жолына – заттың бетін лакпен, бояушы заттармен, эмальмен, резинамен, смоламен, т. б. әртүрлі жасанды (искусственный) пленкалармен жабады, бояйды.
СССР ғалымдары кезінде мынандай патент ұсынған. Ұзын құбырдың ішіне полиэтилен пленкадан жасалған қап (длинный, протяженный мешок надувной) тәрізді ұзын затты еңгізеді. Ол “қап” үрлегенде – ӛзі де құбырдың формасын қабылдайтын үрленген жұмсақ, жасанды құбыр болады, получается искусственный, надувной мешок в виде трубы. Құбырдың ішіне еңгізіп, ауамен үрлегенде – сыртындағы темір құбырға желім арқылы жабысып қалады. Сӛйтіп, темірден жасалған құбырдың жұмыс атқару мерзімін 2-3 есе ұзартатын ішкі, қорғағыш (защитная пленка) қабат пайда болады.
Теңіздегі кемелерді агрессивті коррозиядан қорғау үшін электрлі химиялық әдіс қолданылады. Оны – катодтық әдіс деп атайды. Темірге қарағанда активтілігі жоғары материалды (магний, алюминий, цинк) катод ретінде қолданады. Электр тоқты жақсы ӛткізетін сым арқылы оны кеменің коропусына жалғайды. Анод рӛлін атқарып тұрған осы материалды протектор деп атайды. Сонда коррозия болғанда темірден жасалған корпус емес – протектор (катод) бұзылады, желінеді, азаяды.
Химиялық реакцияны жоғарыда айттық.
Кейде темірден жасалған ӛнім агрессивтілігі жоғары ортада болады. Агрессивтілігі жоғары ортаға қатты қышқылдар (сильные кислоты), сілтілер (щелочи) жатады. Мұндай жағдайда ортаның агрессивтілігін тӛмендету үшін ингибиторлар қосады. Ингибиторлар агрессивті ортаның күшін азайтады.
П. 3. Химиялық элементтердің, металлдардың стандарттық
электродтық потенциалдары
Кейде оны химиялық элементтердің кернеулер қатары деп, немесе вытеснительный ряд металлов те атайды. Орта мектептік бағдарламада аздап айтылуға тиісті. Тағы да бір жолмен – стандартный электродный потенциал металла, қысқаша ряд напряжений металлов деп те атай береді.
Кез келген металлды электролит ерітіндісіне еңгізгенде металлмен электролит шекарасында потенциал айырмасы пайда болады, металл/ерітінді. Электролит ерітіндісі - ол тұздың, кышқылдың, сілтінің судағы ерітіндісі. Әрбір электродтың потенциалы сол металлдың табиғатына, ішкі қасиетіне байланысты. Оны электродты потенциал деп атайды, қысқаша ЭП. ЭП металлдың табиғатына, ерітінде еріген тұздың иондарының концентрациясына, температураға байланысты. Алғашқылардың бірі болып Zn цинк электроды 𝑍𝑛𝑆𝑂4 тұздың судағы ерітіндісінде, Cu мыс электроды 𝐶𝑢𝑆𝑂4 тұздың судағы ерітіндісінде зерттелген. Сол бойынша электродпен сұйықтың (ерітіндінің) шекаралас аймағында потенциал айырмасы пайда болады. Әдебиетте айтылатын Вольта мен Даниель элементтері осылай табылған, зерттелген. Даниель элементінде электрод Cu ( анод) сақталады (массасы ӛзгермейді), ал электрод Zn (катод) - азаяды, массасы кемиді.
Электродтық потенциал кестесі бойынша (таблица 1) Cr, Zn, Mn, Al, Mg, Na, Ca, K, Li элементтері темірге дейін сол жақта тұр. Сондықтан олардың барлығы темірге Fe восстановитель – қалпына келтіруші, толықтырушы элемент болады. Ал керісінше темір оларға қарағанда - оксилитель – қышқылдатқыш болып табылады. 1-ші кестеде кӛрсетілген. Жеке алынған электродтың потенциалын ӛлшеу мүмкін емес. Сондықтан оны стандарттық сутегі электродына байланысты ӛлшейді.
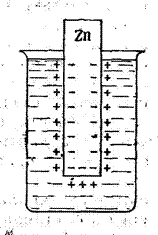
Сурет 1 – Металл-металлдың тұзының ерітіндісі жүйесінде пайда болатын двойной слой потенциалы.
Кесте 1 – Электродтық потенциал кестесі.
Осы стандартты су тегі электродының потенциалын шартты түрде – ноль деп есептейміз. Температураның ӛзгерісі оған әсер етпейді. Сутегі электроды дегеніміз – платина пластинасы. Оның сыртын платиновая черньмен қабаттайды. Планитовая чернь дегеніміз – электролиздік жолмен жиналған (осажденная путем электролиза) аса таза платина. Осы электродты сералық қышқылдың ерітіндісіне салады. Сутегі иондарының концентрациясы 1 моль/литр. Яғни 3-тегі оң жақ ыдыстағы 𝐻2𝑆𝑂4 қышқылы концентрациясы 1 нормальды. Осы су тегі электроды газды сутегі ағынымен үнемі ағылып тұрады, 2, 3 суреттер. Сол жақтағы 1 ыдыста 1 н. 𝑍𝑛𝑆𝑂4 судағы ерітіндісі.
Осы жолмен барлық элементтердің химиялық ЭП ӛлшенген, 1 кестеде келтірілген.
Металлдың активтілігі деген ұғым бар. Электрондарды жеңіл беру қабілетімен сипатталады. Келесі реакция мысалы
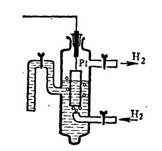
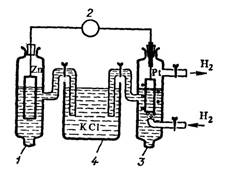
2 – сурет. 3-сурет.
1-1 н. 𝑍𝑛𝑆𝑂4 судағы ерітіндісі, 2 – гальвонометр, 3 - 1 моль/литр, 1
–нормальды 𝐻2𝑆𝑂4 қышқылының ерітіндісі.
Сурет 2, 3 – Электродты потенциалды ӛлшеу схемасы.
𝑍𝑛+𝐶𝑢𝑆𝑂4 =𝑍𝑛𝑆𝑂4 +𝐶𝑢,
(1)
𝑍𝑛+𝐶𝑢2+ =𝑍𝑛2+ +𝐶𝑢.
Мынау қатарда – Zn, Fe, Cu, Ag – алдында тұрған (сол жақ) кейінгі тұрғанды (оң жақ) ерітіндідегі тұздан ығыстырады. Кері бағытта ығыстыру болмайды. Электрондардың металлдағы беріктілігі Zn бастап Ag қарай бағытта ӛседі.
Ығыстыру реакциясы, бір металлдың екінші металлмен ығысуының мәнінде электрондардың ауысуы жатыр, олар бір металлдан екінші металлға ауысады.
𝑍𝑛=𝑍𝑛2+ +2𝑒
(2)
2𝑒+𝐶𝑢2+ =𝐶𝑢.
Гальваникалық элементте пайда болатын э.қ.к. металлдарда бос электрондардың тыңыздығының айырмасына байланысты. Сондықтан әрбір химиялық элементтің ӛз орны бар. Электрондарды беру белсенділігі бойынша. Осы орынды, қатарды кернеулер қатары дейді.
Сонда элементтер былайша орналасқан
…K…Ca…Mg…Zn…Fe…Sn…H…Cu…Ag…Au…
Кернеулер қатарында келесі заңдылықтар орындалады
1) Әрбір металл тұздарда оның оң жағында тұрған металлды ауыстырады. (1), (2) реакциялар.
2) H cутегіден сол жақта тұрған металлдар оны қышқылдан ауыстырады. Ал оның оң жағында тұрғандар – ауыстырмайды.
3) Кернеулер қатарында екі элемент бірінен бірі неғұрлым алыста тұрса, соғұрлым олардың гальваникалық жұбы үлкендеу э.қ.к. ӛндіреді.
𝑍𝑛+𝐻2𝑆𝑂4 =𝑍𝑛𝑆𝑂4 +𝐻2.
Мыстың тұздары суда жақсы ериді. Судың тұтас молекулаларымен байланысады. Соны тұздардың гидраты дейді. Мыстың тұзының гидраты
𝐶𝑢𝑆𝑂4 ·5𝐻2𝑂 мыс купопросы, медный купорос деп аталады, кӛк түсті болады. Цинкінің тұзы судың тұтас молекeлаларымен қосылғанда 𝑍𝑛𝑆𝑂4 ·7𝐻2𝑂 цинк сульфаты пайда болады. Осы кристаллдар түссіз, прозрачный.
Тексеру сұрақтары
1 Периодтық кестедегі қосымша подгруппадағы элементтер неге металлдарға жатады?
2 24 элемент хромның электрондық формуласын жазыңыздар? 3 Металлдық байланыстың қандай ерекшеліктері жоғары электр жіне жылу ӛткізгіштікті тудырады?
4 Пластичность дегеніміз не? Кӛптеген металлдардың жоғары пластикалық қасиетін немен түсіндереді?
5 Металлдың кристалликалық торларының қандай түрлерін білесіз?
6 Металлдың кристалликалық торларында атомдар қабаттары қалай ӛзгереді?
П. 4. Катодтық қорғау кезіндегі реакциялар
Кейбір деректор бойынша темірден жасалған заттардың істен шығуы, жарамсыз болып қалуы коррозия салдарынан 15 % ке дейін жетеді. Коррозия салдарынан металлдық ӛнімдер ӛзінің физикалық және химиялық қасиеттерін жоғалтады. Сол себептен коррозиядан қорғаудың әдістерін пайдалана білу, оларды дамыту ӛте маңызды.
Катодты қорғау әдісін қарастырайық, 1, 2-ші суреттерді қараңыздар [1-
12].
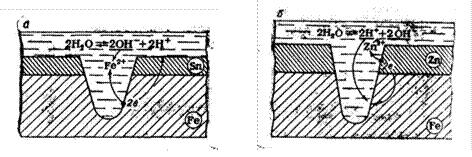
a) б)
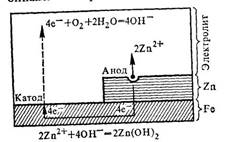
в)
Сурет 1 – цинкінің коррозиялық жұпта бұзылуы, гальваническая пара Zn/Fe [1-9]
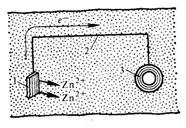
1 – протектор, цинк он корродирует; 2 –тоқ ӛткізуші; 3 – құбырлық жүйе, цинкінің электрондары арқылы қорғалады.
Сурет 2 – жер асты құбырдың протекторлы қорғауы.
Металлдың кернеулік қатарында Fe-ге дейін тұрған келесі элементтердің Cr, Zn, Mn, Al, Mg, Na, Ca, K, Li барлығы катодтық қорғаушы элемент, яғни протектор бола алады.
Сыртқы дымқыл ортада келесі реакция болады [1-9]
4𝑒− +𝑂2 +𝐻2𝑂 =4(𝑂𝐻)− (1)
Соның салдарынан катодта
𝑍𝑛−2𝑒− =𝑍𝑛2+ (2)
Сыртқы ортада
2𝑍𝑛2+ +4𝑂𝐻− =2𝑍𝑛(𝑂𝐻)2 (3)
Анодта, яғни темірдің қасында
2𝐻+ +2𝑒− =𝐻2 (4)
1, 2 –ші суреттер кӛрсеткендей, темір Fe бүлінбейді, ол тек электрондарды тасымалдаушы рӛлін атқарады, Zn – дан сулы ортаға дейін.
Алайда, тереңдетіп қарастырсақ, осы әдебиеттегі теориялық анализ толық емес екені байқалады. Темір Fe мұнда мүлде пассивті элемент ретінде кӛрсетілген. Ол ешқандай реакцияға түспейді, тек қана ӛз бойынын электрондарды ӛткізетін сым, ӛткізгіш, проводник ретінде ғана кӛрсетіледі.
Қалай дегенмен (1) - (4) реакциялар алғашқы потенциал айырмасы неден және қалай пайда болатынын түсіндірмейді. Яғни алғашқы электр тоғы, яғни электрондардың ағыны неге пайда болатынын осы реакциялар негізінде мүлде түсіндіріп бере алмайды.
Сол үшін қосымша келесі реакцияны ескеру керек
𝐻2𝑂 ↔𝐻+ +𝑂𝐻− (5)
Енді (2) мен (4) - ны біріктіріп қарастырсақ ең алғашқы потенциал айырмасы, яғни электродардың ағыны қалай пайда болатынын түсіндіре аламыз. Біздің версиямыз бойынша поляризацияланған дипольды молекула 𝐻2𝑂 ӛзінің теріс полюсты жағымен Zn пластинаға тақайды. Жағдай 3 суретте кӛрсетілген.
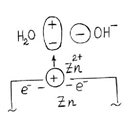
Сурет 3 - Судың поляризацияланған молекуласы және радикал OH- пен цинк атомының кездесуі және әсерлесуі.
Сӛйтіп ең алғашқы оң таңбалы 𝑍𝑛2+ иондары сыртқа шығып (2), (3) реакцияларын бастайды. Пластина катодтың ішінде минус зарядты екі электрон 𝑒− қалады.
Теориялық тұрғыдан анод маңында мынандай реакциялар болады деп ойлап қалуға болады, бір қарағанда
𝐹𝑒−2𝑒− =𝐹𝑒2+ (6)
𝐹𝑒2+ +2𝑂𝐻− ↔𝐹𝑒(𝑂𝐻)2 (7)
𝐹𝑒(𝑂𝐻)2 =𝐹𝑒2+ +2𝑂𝐻− (8)
𝐹𝑒2+ +2𝑒− =𝐹𝑒 (9)
(9) реакцияcы пластинадан бӛлініп, жоғалып кеткен темір атомдары қайтадан сан бойынша қалпына келетінін кӛрсетеді. Алайда электролиздік процесстің болмауына байланысты, осы темір атомдары қайтадан темір пластинаға жабысып, сол пластина бұзылмайды, ыдырамайды деп айта алмаймыз.
Zn активтілігі жоғары, ал Fe активтілігі тӛмендеу болады, металлдардың электрліктік химиялық кернеулер қатары бойынша, немесе оны стандарттық электродтық потенциал дейміз [1-9], бірінші кесте. Сол себептен (2)-(4) реакция жақсы интенсивті жүреді, ал (6) мен (7) – жүрмейді.
Химия элементінің электрлік химиялық кернеулер қатары бойынша Zn активтілігі Fe-нан жоғары болғандықтан (1) - (4) реакциялар болады, ал (6)-(9) реакциялары мүлде жүрмейтінін дәлелдеп шығайық.
Сонымен қоса сулы, дымқыл ортада Fe-Zn-𝐻2𝑂 жүйесінде Даниель элементіне сәйкес, соған тән реакциялар да қосымша жүреді деп теория бойынша ойлауға болады. Cол бойынша дымқылды құмды, топырақты ортаға 𝑍𝑛2+ иондарымен қоса 𝐹𝑒2+ иондары да қоса бӛлініп шығады деп ойлап қалуға болады, алғашқыда. Жоғарыда кӛрсеткендей. Алайда олай болуы мұмкін емес. Себебі, Даниель элементінің теориясы бойынша Fe – оң заряд алар еді яғни анод болады, ал Zn – теріс зарядталады, яғни ол катод болар еді. Сыртқы орта бойынша сонда электрондар катодтан анодқа қарай ағады, яғни цинк пластинадан – темір пластинаға қарай ағады. Ерекше айтамыз – бұл тоқ онда сыртқы орта бойынша жүрер еді, яғни ылғалды топырақ бойымен. Алайда осы тоқ 3 суреттегі б, в және 4 – суреттегі электр тоғына қарама қарсы болғандықтан – мүлде болмайды. Яғни (6)-(9) реакциялары мүлде жүрмейді деуге болады. Себебі олар (1)(4) реакцияларындағы электр тоғының ӛту бағытына қарама-қарсы, яғни кері бағытталған. Сӛйтіп (6)-(9) реакцияларындағы темірдің сыртқы ортаға шығып жоюлу реакциясы мүлде болмайтынын дәлелдеп шықтық.
(1)-(4) реакция жолдары оттегісіз де жүре алатынын кӛрсетейік
Катодта келесі реакциялар болады
𝐻2𝑂 ↔𝐻+ +𝑂𝐻− , (10)
𝑍𝑛−2𝑒− =𝑍𝑛2+ , (11)
𝑍𝑛2+ +2𝑂𝐻− =𝑍𝑛(𝑂𝐻)2 . (12)
Ал анодта келесі реакция жүреді
2𝐻+ +2𝑒− =𝐻2 . (13)
1-в суретіндегі (1) - (4) реакциялар және (10)-(13) реакциялар қатар, параллельно жүреді деп тұжырымдаймыз.
Кейбір әдебиетте цинк пластинасын – анод, ал темірді – катод деп атап кеткен. Осыны жәй техникалық қателік деп түсінеміз. Себебі электр тоғы электрондардың ағынымен сипатталады. Электрондар әрдайым потенциал - кернеу тӛменгі электродтан – кернеу - потенциал жоғары электродқа қарай ағады. Коррозиядан, даттанудан қорғау әдісін қарастырсақ, электрондар цинк Zn пластинадан – темір Fe пластинаға қарай ағады, 1, 2 суреттер. Сондықтан, әлбетте цинк – катод, ал темір – анод. Қосымша, электронды лампаның жұмысын қарастырыңыздар [10 -
12].
Теориялық жаңа тұжырымдарымыз түсінікті болу үшін [10] әдебиетте Даниель, Вольта элементерінде э.қ. к. қалай пайда болатыны қалай түсіндірілгенін қарастырайық. Оны жеке параграф ретінде қараймыз.
П. 5. Гальваникалық элементте тоқ және э.қ.к. қалай пайда болады
1 суретте Cu және Zn электродтары 𝐻2𝑆𝑂4 күкірт қышқылы ерітіндісіне салынған. Цинк және мыс электродына жалғанған сымдарды сырттағы тізбек бойынша гальванометрге жалғаса потенциал айырмасын кӛрсетеді. Осы Вольта элементі болады. Алғашқыда 𝑒 ≈ 1,1 В кернеу шығады. Кейін ол күрт азаяды. 𝑒 нің тез азаюы электродтардың поляризациялану эффектісінен болады. Поляризациялану туралы жеке параграфта айтамыз.
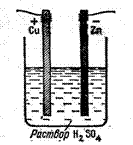
1 Сурет. Вольта элементі.
11-суретте Даниеля элементі кӛрсетілген. Онда Cu пластинасы судағы 𝐶𝑢𝑆𝑂4 ерітіндісіне сол жақта, ал оң жақта Zn - 𝑍𝑛𝑆𝑂4 судағы ерітіндіісіне салынған. Металлдық электродтан 𝑍𝑛2+, 𝐶𝑢2+ иондары ерітіндіге (суға) шығатыны жеке 2 – суретте кӛрсетілген.
Сурет 2– Цинк Zn және 𝐻2𝑆𝑂4 қышқыл ерітіндісі арасында потенциал айырмасы пайда болу схемасы.
Оң таңбалы иондар ерітіндіге шыққанда олардың электрондары металл ішінде қалып қояды. Неге дәл солай болатыны – жалпы әдебиетте түсіндірілмейді. Осы ӛте қызықты және құпиялы физикалық және химиялық құбылыс. Металл иондарының сыртқы орта, яғни ерітіндіге шығу себебін 3 сурет (п. 5 ) бойынша түсіндіре аламыз. 𝑆𝑂42− минус ионы Zn пластинаға тақайды. Тіпті ол толық ыдырамаған, екіге бӛлінбеген, тек қана поляризацияланған, диполь сияқты молекула болуы мүмкін.
Сурет 3 – Даниель элементінің жұмыс жасау схемасы [1-9].
Осы молекула теріс зарядталған
бүйірімен Zn пластинаға тақайды да Zn атомын ӛзі де
поляризациялайды. Яғни оны дипольды атомға айналдырады. Екі диполь
бір біріне қарама қайшы, яғни бір бірін тартатын
бүйірімен қарайды. Осы жағадай 3 суретте кӛрсетілген.
Нәтижесінде ерітіндіге 
, 
металл
иондары сұйыққа, ерітіндіге шығады. Неге Cu пластина
оң (+) таңбалы (яғни анод), ал Zn пластина минус (-)
таңбалы (катод) болып шығатынын әдебиетте түсіндіреді.
Ең жақсы, анық, айқын түсіндіру – ол Ландсберг Г.
С. кітабы. Сол бойыншы Cu мен 
ерітіндісі арасында
минус 
потенциал айырмасы пайда болады. Сол
сияқты Zn мен 
арасында минус 
потенциал айырмасы пайда болады. Қышқылдың судағы ерітіндісіндегі потенциалды нольдік потенциал деп есептейік. Яғни ерітінді – санақ жүйесінің бастауы, начало системы отсчета, начало нулевого уровня. Сонда қорытынды потенциал айырмасы болады
.
Таңбасы плюс. Яғни мыспен цинк арасындағы потенциал айырмасы оң таңбалы болады.
Осы екі пластинаны сыртқы тізбекпен сыммен жалғаса – электр тоқ жүреді. Электрондар цинк пластинадан мыс пластинасына қарай ағады. Сондықтан мысты анод, цинкіні – катод деп атағанымыз әбден дұрыс болады. П.5, 1-в суретте кӛрсеткендей кейбір кезде осы екі пластинаны қате, керісінше атап кеткен кездер болады. Жүйелік емес, жәй техникалық қателік деп түсінуге болады.
Оң жақ камерада кетіп жатқан
электрондарды толықтыру үшін 
иондары ерітіндіге
шыға береді қосымша. Сол жақ камерада 
иондары Cu
пластинаға тақап, электролиздік жабысады, 
. Содан бос 
иондар кӛбейеді. Олар
ортадағы перегородка арқылы оң жақ камераға
ауысып келесі қосылу реакциясына түседі
.
(14)
Cӛйтіп сол жақ камерада
ерітінді ішіндегі 
азаяды, ал оң жақ
камерадағы 
кӛбейеді. Даниель элементі
тұрақты жұмыс жасау үшін сол жақ камераға 
қосып отырады, ал оң
жақ камерадан 
тұзын тұнба ретінде
кӛбейгенде алып, тӛгіп тастап, слив жасап
отырады.
Әдебиетте келесі сұрақ айтылмаған. Ерітіндіде химиялық элементтердің электродты потенциалы пайда болу құбылысына физикадағы электрондардың шығу жұмысының әсері, байланысы бар ма, әлде жоқ па?
Осы сұрақты мен әлі толық зерттеген жоқпын. Тек физикалық интуиция ретінде әзірше – иә, байланыс бар деп жауап бергім келеді. Электрондардың металдан шығу, ұшу физикалық құбылысы Эйнштейн формуласымен сипатталады [10-12]
,
мұнда - толқын жиілігі, - Планк тұрақтысы.
Сурет 4 - 𝐻2𝑆𝑂4 қышқылдың судағы ерітіндісіндегі гальваникалық элемент
4-суретте күкірт қышқылы 𝐻2𝑆𝑂4 судағы ерітіндісіндегі
гальваникалық элемент жұмыс жасайтын гальваникалық элемент кӛрсетілген. Оны да Даниэль элементі дейді. Бұрынғыдан айырмашылығы неде? Мыс электродында 𝐻+ иондары жиналып мыстан электрондарын тартып алып нейтральды атомдар 𝐻2 пайда болады. Сӛйтіп осында поляризация дереу (сразу) жүреді. Поляризация туралы алдағы параграфта айтылады.
П. 6. Э.қ.к. химиялық энергия сақталу негізінде есептеу
Химиялық тоқ ӛндіру негізінде екі электродтар және электролит арасында химиялық түрде энергия бӛліну заңдылықтары жатыр. Даниель элементінде екі реакция жүреді: 1 – Zn ериді де 𝑍𝑛𝑆𝑂4 тұзы пайда болады, (14) реакция. 2 - 𝐶𝑢𝑆𝑂4 суға ериді, ыдырайды. Cu пластинасында мыс ионы восстановление болып мыс пластинасына жабысады, қосылады. Яғни мыс пластинаның салмағы кӛбейеді.
𝐶𝑢2+ +2𝑒− =𝐶𝑢.
Бірінші реакция энергия шығарады, екінші реакция энергияны қабылдайды, жұтады. Шығарылған, жұтылған энергияны калолиметрмен ӛлшейді. Пластинадан бір моль цинк шыққанда шығарылған энергия мӛлшері 𝐸1 =4,4∙105 Дж.
Мыс пластинадағы жоғалатын (жұтылатын) энергия мӛлшері тең 𝐸2 =2,34∙105 Дж. Бұл 1 моль Cu атомы мыс пластинаға - анодқа жабысқанда (қосылғанда) жұтылатын энергия мӛлшері.
Қорытынды, пайдалы болып есептелетін энергия мӛлшері тең болады 𝐸 =𝐸1 −𝐸2 =2,06∙105Дж. Осы - 1 моль цинк еріп, ал 1 моль мыс ерітіндіден анодқа шыққанда, қосылғандағы пайдалы энергия қоры, запасы.
Енді осыдан теория бойынша Даниель элементінің э.қ.к. қандай болатынын есептеуге болады. Сыртқы тізбектен ӛтетін тоқ мӛлшері ӛте аз болғандықтан пластаналар арасындағы кернеу 𝑈 ≈𝑒 деп есептейміз, 𝑒 – ӛндірілетін э.қ.к. Екінші электрод мыста 1 моль Cu шыққанда тоқтың жасайтын жұмысы 𝐴=𝑞∙𝑈. 𝑞 =2∙96484, себебі мыс 2 – валентті. Сонымен тоқтың жасаған жұмысы тең 𝐴=2∙96484∙𝑈 [Дж] = 1,93∙
105 𝑈 [Дж]. Тоқтың жасаған осы жұмысы химиялық реакция бойынша ӛндірілетін энергияға тең болу керек. Содан
1,93∙105 ∙𝑈 =2,06∙105Дж.
Осыдан 𝑈 =1,07 𝐵 шығады. Осы есептеумен тапқан 𝑒 мәні оның шын, тәжірибелік мәніне жақын, 𝑒 =1,09 𝐵.
П. 7. Zn пластинасындағы паразиттік тоқ
Цинк пластинаның азайып ерітіндіге ион ретінде бӛлініп шығуы сыртқы тізбек арқылы тоқ жүргенде ғана болады. Сыртқы тізбек ашық, жалғаусыз күйде тұрғанда 𝑍𝑛2+ ионы ерітіндіге шықпайды, яғни сонда цинк азаймайды. Практикада алайда 𝑍𝑛2+ иондары ерітіндіге бӛлініп шығады екен. Сыртқы тізбек ашық болса дағы. Себебі паразиттік тоқта. Цинк пластинасы аза таза болмауы мүмкін. Оның ішінде, құрамында басқа металлдардың, элементтердің қоспалары болуы мүмкін. Мысалға цинк пластина ішінде Fe элементінің молекулары болуы мүмкін. Сонда Fe-Zn-ерітінді жүйесінде паразитті тоқтар ӛздігінен пайда болады. 1-ші суретте кӛрсетілген.
Сурет 1-Гальваникалық элементте паразитті тоқтың схемасы.
Таза емес, қоспалары бар цинк пластинасы кислота немесе металл тұзының ерітіндісіне батырылса гальваникалық элемент болып жұмыс жасай бастайды. Ол ӛз – ӛзіне жалғанған, тұйықталған, короткозамкнутый элемент болып шыға келеді. Осындай тоқты паразитный тоқ деп атайды. Ол пайдалы электродтың (цинк, мыс тағы да басқа) мүжілуын, кемуін, азаюын тудырады. Осындай теріс процесстерді болдырмау үшін платинаны, электродты аса таза қылып жасау керек, немесе жұмыстан бос уақытта ерітіндіден шығарып, сыртқы құрғақ ауада сақтау керек. Электрод, пластина (немесе құбыр) цинктен емес, темірден Fe жасалған болса, онда Ni – ден бастап Au – ға дейінгі элементтердің қоспалары оған теріс паразитті әсер етеді. 1-ші кестені қараңыздар.
П. 8. Электродтар поляризациясы
Вольта элементін амперметр арқылы жалғағанда бастапқы тоқ (немесе э.қ.к.) күрт азаяда бастайды. Бірнеше минут ӛткенде бастапқы мәні бірнеше есеге азаяды. Сонымен Вольта элементі практикада қолдануға келмейді. Неге осылай болатынын қарастырайық. Жауап түсінікті болу үшін келесі тәжірибені қарастырамыз. Аздап қышқылдатылған суға екі бірдей электрод салынады. Қышқылданған суда аз мӛлшерде күкірттік қышқылы болады. Екі бірдей электрод екі кӛмірлі немесе екі платиналы болуы мүмкін. Сымдармен сыртқы тізбекті амперметр арқылы жалғаймыз, 1-а суретте амперметр ешқандай тоқ кӛрсетпейді. Бұл түсінікті. Екі бірдей электродтар (уголь-уголь) арасында ешқандай потенциал айырмасы болмайды, U=0.
а)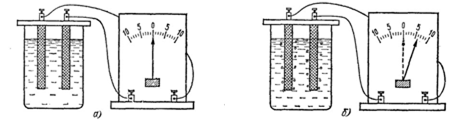 
б)
Сурет 1-а бастапқы кезедегі жағдай, нейтральды жағдай 1-б электролизден кейінгі жағдай, поляризация тоғы
Сымдарды ажыратып сырттағы тоқ генераторына немесе э.қ.к. жалғайық. Тізбектен тоқ ӛте бастайды. Күкірт қышқылының электролизы басталады. Тоқты тасымалдайтын иондар 𝐻2𝑆𝑂4 →2𝐻+ +𝑆𝑂42− . Минус электродта сутегі 𝐻2 , екінші плюс электродта оттегі 𝑂2 пайда болады. Екінші плюс электродта келесі реакция орынды
.
2𝑂− −2𝑒− =𝑂2 .
Сымдарды тоқ кӛзінен ажыратқанда осы екі электрод сол газ кӛпіршңктермімен қоршалған болып тұрады. Енді сымдарды қайтадан жадлғайық, тізбекті қосайық. Осы кезде сыртқы тізбек сымдар арқылы оттегімен қоршалған электродтан сутегімен қоршалған электродқа қарай тоқ жұре бастайды. Яғни тоқтың бағыты 𝑂2 → 𝐻2. Электрондар катодтан анодқа қарай ағады. Ал электротехникада тоқтың бағыты плюстан минусқа қарай бағытталған, яғни электрондардың ағынына қарама қарсы бағытта тоқ ӛтеді. Осы тоқ тез азаяды. Сонымен қоса электродтардағы газда азаяды. Газ біткенде тоқта бітеді.
Электродтарды екі түрлі газ сыртынан орап қоршап тұрғанда олардың әрқайсысының ерітінді (растворға) байланысты потенциалдары ӛзгереді. Сӛйтіп кӛмірлі электродтар батареяның полюстары құсап кетеді, яғни гальваникалық элементке айналады. Осы құбылыс электродтардың поляризациясы (поляризация электродов) деп аталады. Екі электрод арасында пайда болатын э.қ.к. – поляризация э.қ.к. деп аталады, 𝐸𝑝. Сұйық (ерітіндіде) ішінде де тоқ жүріп жатады. Мысалға минус зарядты сутегі ионы 𝐻− минус зарядты (-) цинк электродынан шығып плюс зарядты (+) мыс электродына қарай аға бастайды. Оң таңбалы мыс электроды қасында 𝑂2 пайда болады. Минус таңбалы цинк электроды қасында 2𝐻 =𝐻2 сутегі атомдары жиналады. Осы екі газ 𝐻2 , 𝑂2 электродтарда қосымша э.қ.к. 𝐸2 пайда болғызады. Ол Вольта мен Даниельдің батареясы тудыратын негізгі э.қ.к. 𝐸1-ге қарама қарсы, кері бағытталады. Сол себептен осы химиялық элементтердің тоқ кӛзі ретінде жұмыс жасауы нашар, қабілетсіз болады.
Электродтар мағында газды элементтердің жиналғаны теріс роль атқарады. Газды ортада электролит тоқты нашар ӛткізеді. Себебі металлды электродпен иондары бар электролит арасында қонтакт беті азаяды.
Гальваникалық элементтерде поляризация пайдалы емес деген тұжырымға келеміз.
П. 9. Гальваникалық элементтердің деполяризациясы
Минус, теріс зарядталатын электрод негізінде негізінен цинк қолданады. Қышқыл ерітіндісіне шыққан 𝑍𝑛2+ цинк иондары сондағы минус 𝑆𝑂42− қышқылдың қалдығы иондармен қосылады. П. 6 дағы (14) реакция жүреді. Ендігі мақсат – газдың бӛлініп жиналуын болдырмау. Сонымен деполяризация мақсаты – плюс электродта сутегі атомдарын болдырмау.
Кәзіргі кезде негізінен химикалық деполяризацияны қалданады. Сол бойынша ерітіндіге күшті қышқылдатқыш еңгізеді. Ол электрод маңында пайда болып жатқан сутегі атомдарымен химиялық реакцияға түсіп, оның жеке газды түрінде пайда болуын тоқтатады.
Гальваникалық элементтердегі деполяризация мысалдарын қарастырайық. Деполяризация дегеніміз – поляризацияны жою, нольге түсіру. 1 суретте Лекланше гальваникалық элементінің құрамы кӛрсетілген. 1 а - суретте стержень С – кӛмірлі электрод, сыртында цинктен Zn жасалған цилиндр, ол екінші электрод. Қышқылды сұйық – ол хлорлық аммонийдің судағы ерітіндісі, нашатырь ерітіндісі 𝑁𝐻4𝐶𝑙 . Деполяризатор ретінде марганец перекисі, марганецтің екі окисі 𝑀𝑛𝑂2 қолданады. Кенеп қапты ұнтақталған 𝑀𝑛𝑂2 порошогымен толтырады. Ортасына кӛмірлі стержень С орналастырады. Арасына ұнтақталған графит порошогын де қосады. Тоқ ӛткізгіштігін кӛтеру үшін. 1 – а суретте кӛрсетілген. Сутегі атомдарын жойып отыратын реакция келесі болады
𝑀𝑛𝑂2 +2𝐻 =𝑀𝑛𝑂+𝐻2𝑂.
Сутегі атомы деполяризатордың оттегі атомдарымен қышқылданады, су молекуласына айналады. Сӛйтіп газды түрге айналмайды. Лекланше элементі жуықтап э.қ.к. 1,4 В береді.
а)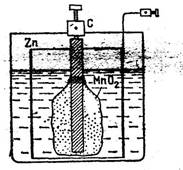 
б) 
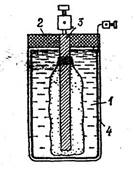
Сурет 1 - а – Лекланше гальваникалық элементі, б – Лекланше құрғақ элементі.
1-б суретінде құрғақ Лекланше элементі кӛрсетілген. Сұйық электролит орнына аса қою клейстер пайдаланған. Ішінде орта тұсында нашатырь бар. Крахмалдық масса (клейстер) 1-б суретте 1 деп белгіленген. 2 – смола сағыз, жоғарыдан құйылады. Батарея тӛңкерілгенде ішіндегі заттар тӛгіліп қалмаудан және ауаға кетіп кеуіп қалмаудан сақтайды. 3-кӛмірлі электрод жіңішке стержень ретінде, 4-цинковый электрод сыртқы цилиндр, қорап рӛлін атқарады. Кішкентай қалталы фонариктердің батерядары осындай болады.
Даниель элементінің бір жақсы жағы – онда поляризация болмайды. Катод (Zn) қасында суретте 𝑍𝑛𝑆𝑂4 пайда болады, п. 6 формула (14).
Анодта (Cu пластинасы) таза Cu пайда болып пластинаға қосылады. Сӛйтіп екі электродтардың беті таза болып тұрады, онда газды 𝐻2 , 𝑂2 болмайды.
Соңғы кезде ауалы деполяризатор қолданыста болып келеді. Сутегі атомын оттегі атомымен қышқылдатып жіберу үшін ауамен катодты үрлейді. Ауаның ішіндегі оттегі атомдары сутегі атомдарымен реакцияға түсіп су молекласы пайда болады 𝑂2 +2𝐻2 =2𝐻2𝑂.
П. 10. Аккумуляторлар.
Жоғарыда айтқандай поляризация эффектісі – зиянды. Алайда оны пайдалы етуге де болады екен. 1895 жылы Планте поляризация э.қ.к. пайдалы етіп пайдалану жолдарын тапты. Сол үшін ол келесі аккумулятор деген жаңа э.қ.к. ойластырды. Қорғасыннан жасалған екі электрод 𝐻2𝑆𝑂4 күкірт қышқылы ерітіндісіне салынады. Екі электрод бірдей болғандықтан э.қ.к. 𝐸 =0 болады. Осы жүйеден біраз уақыт тоқ ӛткізеді, п. 9 қараңыздар. Электролизден пайда болған элементтер электродтармен әсерлеседі. Сол себептен электрод материалдары ӛзгереді, олар екі түрлі электрод болып шығады. Яғни олардың химиялық құрамы ӛзгереді. Сол себептен екі электрод арасында поляризация потенциалы пайда болады. 𝐸 =2 V болады. Сыртқы тоқ кӛзінен ажыратқан сон, осы элемент ӛзі дербес тоқ кӛзі, яғни ӛзі тоқ генераторына айналады. Енді осы тоқ генераторын сымдар арқылы тоқты тұтынатын жүктемеге жалғасағанда сыртқы тізбек арқылы тоқ жүре бастайды. Осы пайдалы тоқ біраз уақыт бойы болады, уақыт ӛте келе біртіндеп күшін жоя бастайды. Осы тоқ кӛзін аккумулятор деп атайды.
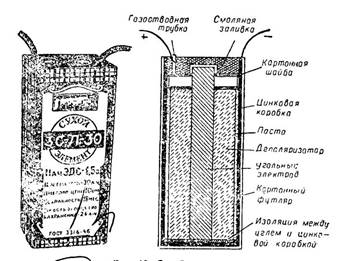
Сурет 1 – Құрғақ элемент
Күші бітіп қалғанда аккумуляторды сыртқы тоқ кӛзіне жалғап поляризацияны қайтадан жасайды. Осыны аккумулятордың зарядкасы дейді. Планте элементіне ұқсас принциппен жұмыс жасайтын барлық заряд жинаушы құрылғыларды аккумулятор деп атайды.
1 – суретте құрғақ элемент, сухой элемент деп аталатын батарея кӛрсетілген. Цинк қораб минус клемма болады. Осы элементтің
деполяризаторы нашатырь ерітіндісімен толтырылған. Электролит – ол паста. Картофельді және бидай ұнының қоспасынан жасаған, нашатырьмен араластырады. Ӛндіретін E ~1,45÷1,5 В, ішкі кедергі 0,3 ÷ 3 Омға дейін ӛзгереді. Бірнеше осындай сухой элементтің қосындысын батарея деп атайды.
П. 11. Электрлік қозғалтқыш күш э.қ.к.
Жалпы электр тоғын түсіндіру әдісі батареяның екі клеммасы, яғни екі электрод негізінде атқарылады. Плюс және минус клеммалар. Электр лік потенциалы жоғары – ол плюс, ал одан тӛмендеуі – минус. 𝜑1 >𝜑2, 1-ші э.қ.к. қарастырайық. 1-ші суретте химиялық тоқ кӛзін қарастырайық. Ыдыста хромдық қышқылдың 𝐶𝑟𝑂3 және 𝐻2𝑆𝑂4 күкірт қышқылының судағы аз мӛлшердегі ерітіндісі, в малом количестве, слабый, разбавленный раствор деп атайды. Бір электрод – цинк Zn, екінші электрод – кӛмір.
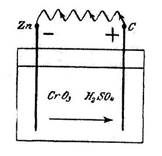
Сурет 1 – Э.қ.к. түсіндіруге тоқ схемасы.
Тоқтың бағыты стрелкамен кӛрсетілген. Сырттағы тізбекте электрондар аға бастайды. Алайда уақыт ӛте келе тоқ азаймайды, ол жүре береді. Яғни электрондар ағыны электродтарда тоқтап қалмайды, олар ерітінді ішінде де бір полюстан екінші полюске дейін аға береді. Яғни электр тоғы тұйықталған контур бойынша циркуляция заңымен жүре береді. Олай болмаса, электрондар кӛмір электродында жиналып қалса дереу ∆𝜑 = 𝜑1 −𝜑2 =0 болар еді. Сонда тоқ тоқтап қалады. Ерітінді ішінде электрондар ағынын қамтамасыз етіп тұрған күшті электрлік қозғалтқыш күш э.қ.к. деп атайды. Кӛп жағдайда келесі әріптермен белгілейді: E, ε, U. Ӛлшегіш техника дамымаған кезде E мӛлшерін электроскоптың жапырақтарының бір-бірінен алыстау, тебіну мӛлшерімен анықтаған. Электроскоп жапырақтарына алтынды да жаққан кездері болған. Кәзіргі кезде э.қ.к. ӛлшейтін приборлар кӛп, оның ішінде цифрлы мультиметрлер де кӛп тараған. Қарапайым тілде – ЦЭЖ-ка деп атап кеткен. E ні тоқ мӛлшерімен де ӛлшейді.
1, 2 – суреттер және кесте 1 А. Томелен. Основы электротехники.-С.Петербург.-1911. - 622 с. – кітабынан алынды. Ғылыми және оқытулық әдебиеттерде орыс тілінде басылған кітаптар ӛте кӛп, оның ішінде осы кітап неміс тілінен аударылған. Кітаптардың кӛбісі интернет арқылы бұл күндері қол жетімді, кӛп жағдайда тегін. Ресей қуатты мемлекет. Маңызды деген ағылшын тілінде бар әдебиеттердің негізгі кӛлемін олар орыс тіліне дер кезінде аударып, шығарып отырады. Кӛп жағдайда шет елдік әдебиеттерді орыс тіліне аударылған варианттарын олармен ортақ интернет қордан алып пайдаланған бізге әлдеқайда ыңғайлы, тиімді және жылдам.
Айтарлықтай кӛп жылдық біздің оқытушылық, ғылыми-техникалық практика осыны кӛрсетеді.
Кесте 1 – әртүрлі қышқылды ортада, әртүрлі ерітіндіде пайда болатын Э.қ.к.
Сондықтан ағарту, оқытулық, білім беру саласында Ресей федерациясының аса бай әдебиет қорын пайдалана білу – ӛте дұрыс, құптарлық және тиімді іс болады бізге. Бұл жолда біздің алфавитіміздің кириллица графикасында болғаны – біз үшін ӛте үлкен бақыт, жақсы жетістік, ӛте дұрыс, қуанарлық шаруа.
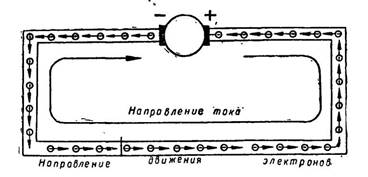
Сурет 2 – Электротехникадағы тоқ бағыты және электрондар ағыны.
2 суретте электротехникадағы (ЭТ) тоқ бағыты және электрондар ағыны кӛрсетілген. Екеуінің бағыты қарама карсы.
П. 12. Ом заңы.
Бір ыдыста су болсын. Екінші бос ыдыс одан h – қашықтықта тӛмен тұр. Екінші ыдысты біріншімен құбыр, немесе резина шланг арқылы жалғайық. Бірінші жоғарыдағы ыдыстан екіншіге қарай су ағады. Судың ағын жылдамдығы немесе кӛлденең қимадан бір секундта ӛтетін су шығыны G (кг/сек) потенциал энергияның айырмасына ∆П=𝑚𝑔 пропорционал болады 𝐺~∆П.
Сурет 1 – Тізбек бӛлігі, толық емес тізбек
Сол сияқты сымның кӛлденең кимасынан ӛтетін тоқ мӛлшері сол сымның екі жақ шетіндегі потенциал айырмасына пропорционал болады, ал кедергіге кері пропорционал болады
.
(1)
Мұнда 𝑈 =𝜑1 −𝜑2 - потенциал айырмасы, В, R – кедергі, Ом.
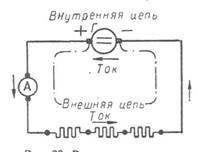
Сурет 2 – Толық тізбек, түйықталған тізбек.
-
(2)
тоқ күші, А, ∆𝑞 - заряд мӛлшері, Кл, ∆𝑡 - уақыт, секунда.
(1) – Ом заңы.
Генератортың ішіндегі сымдардың кедергісі ішкі кедергі - 𝑅вн =𝑅1, ал сыртқы тізбектегі кедергі 𝑅внеш =𝑅2. Осындай толық, тұйықталған тізбекке Ом заңы келесі түрде жазылады
,
Мұнда 𝐸 - генератордың э.қ.к., I – амперметрден ӛтетін тоқ.
Әдебиет
1 Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика.- М.: Металлургия, 1973. -256 с.
2 Лушпа А. И. Основы химической термодинамики и кинетики химических реакций.- М.: Машиностроение, 1981. – 220 с.
3 Иноземцев Н. В. Основы термодинамики и кинетики химических реакций. – М.: Военная академия механизации и моторизации красной армии имени Сталина, 1940. -254 с.
4 Телеснин Р. В. Молекулярная физика.- Москва: Высшая школа, 1973. –
360 с.
5 Бродский А. И. Физическая химия. Том 1. – Свойства материи, химическая термодинамика. – М.- Л.: Гос. науч.-техн. изд. химич. лит-ры, 1948. – 488 с.
6 Киреев В. А. Курс физической химии. – Москва: Химия, 1975. – 776 с. 7 Даниэльс Ф., Альберти Л. Физическая химия.- Москва: Высшая школа, 1978. – 780 с.
8 Хомченко Г. П. Химия.-Москва: Высшая школа, 1989. -368 с.
9 Глинка Н. Л. Химия общая. – Москва: Интеграл - Пресс, 2003. -728 с.
10 Ахметов Н. С. Общая и неорганическая химия. – Москва: Высшая школа, 2001 . – 743 с.
11 Полинг Л., Полинг П. Химия. Переводное издание с англ. языка. – Москва: Изд-во Мир, 1978. - 683 с.
12 Неницеску К. Общая химия. Переводное издание с румынского языка.- Москва: Изд-во Мир, 1968. – 793 с.
13 Некрасов Б. В. Основы общей химии. Том 1. – Москва: Химия, 1973. – 656 с.
14 Некрасов Б. В. Основы общей химии. Том 2. – Москва: Химия, 1973. –
688 с.
15 Никольский А. Б., Суворов А. В. Химия. – Санкт Петербург: Химиздат, 2001. – 512 с.
16 Петров М. М., Михилев Л.А., Кукушкин Ю. Н. Неорганическая химия. – Ленинрад: Издат. Химия, 1981. - 543 с.
17 Карапетьянц М. Х., Дракин С. И. Общая и неорганическая химия. – Москва: Химия, 1992.- 592 с.
18 Ландсберг Г. С. Элементарный учебник физики. Том 2.
Электричество и магнетизм. – Мосвка, АОЗТ Шрайк, 1995. – 479 с.
19 Сивухин Д. В. Электричество. Общий курс физики.-Том 3. – М:
Наука, 1979. – 680 с.
20 Савельев И. В. Электричество. Курс общей физики. – Том 2. – Москва: Наука, 1982 г. – 425 с.
21 Иродов И. Е. Основные законы электромагнетизма. – Москва: Высшая школа, 1991. - 288 с. 22 Касаткин А.С., Немцов М. В. Курс электротехники. – Москва: Высшая школа, 2005. – 542 с.
Жакатаев Т. А.
Нұр-Сұлтан қ., 2020 ж.
Жакатаев Т. А., техника ғылымдарының докторы
Квазистатикалық процесс. Қайтарымды, қайтарымсыз процесстер
V=const болғандағы химиялық реакцияның жылулық эффектісі
Аккумуляторлар 178 8
Соңғы тарауда коррозия теориясы, соған байланысты электрлік химиялық процесстер тәптішті түрде баяндалған
Және де сол потенциалды энергия ӛзгермелі функция
П. 3. Гей-Люссак, Шарль заңдары
V=V(t) түзу сызығын t - ның минус жағына жалғастырса, кӛлем кішірейе береді және 0
Мұндағы тұрақты тек қысымға ғана тәуелді, температураға байланысты емес
Эксперимент кӛрсеткендей
Ж. А. Шарль заңы, 1787 ж. табылған
Олардың белгілі бір қасиеттері болады
Гей-Люссак әртүрлі газдардың химиялық реакцияға түскендегі кӛлемдерін зерттеді
Эксперимент арқылы нормальды жағдайда бір литр 𝑂 2 оттегінің салмағы 𝑚 1 =1,43 г екені анықталған
Кез келген атомның массасы = 1,66·10 -27 · кг, кез келген молекуланың массасы = 1,66·10 -27 · кг
Тұрақты 𝑟 (P,V,T) – лардан тәуелді емес
Мұнда 1 моль газдың кӛлемі,
К (2) 1 кал = 4,19
Ауаға μ В =28,98 , су тегіне μ 𝐻 =2,016 г/моль
Парциалдық қысым тең
Екіншіде молекулалар (шарлар) үнемі қозғалыста болады, тепловое движение, жылулық қозғалыс
Ол 1 секунда ішінде 1 см 2 қабырға ауданына қаншама молекула (шар) келіп соғылады, соған байланысты
Н. Молекулалар кеңістік бойынша бейтарап бағытталған, бейберекет қозғалады
P - (ABCD) қабырғаға әсер ететін жалпы қысым,
Сонда
П. 14. Молекуланың хаотикалық қозғалысының энергиясын бостандық дәрежесі бойынша таралуы, бӛлінуі
Кейіннен білінді, әрбір степеньге энергия тең бӛліну заңы тек классикалық физикада ғана орынды екен
Сондықтан соған сәйкес бұрыштық айналу жылдамдық ӛте жоғары болады
Сонда = kT
C] = [Дж/(моль·К)]. Кӛлем тұрақты болғанда жұмыс жасалмайды, 𝛿𝐴=0
![C] = [Дж/(моль·К)]. Кӛлем тұрақты болғанда жұмыс жасалмайды, 𝛿𝐴=0](https://fs.znanio.ru/d5af0e/30/6f/97aa384951f6dd514b7187dfac69fd1f93.jpg)
Сурет 1 – Газдың кӛлемі ұлғайғандағы жұмыс (1) ді дәлелдейміз
Адиабата процесі. Осында жүйе ( яғни кӛлемдегі газ) сыртқы ортаға жылуды бермейді, және қабылдамайды да
Немесе
Осы екі жағдай адиабатаға жуықтап келеді
Осыдан болады 𝑃𝑉 𝛾 =𝑐𝑜𝑛𝑠𝑡
Оның ішіне бәрі кіреді: изобара, изотерма, адиабата, изохора
P, V, T параметрлер жоқ. Сондықтан политропадағы жылу сыйымдылық тұрақты болады
Бірінші жағдайды қарастырайық
Изохоралық процессте жұмыс нольге тең
Сондықтан тәжірибелік процесстерді жуықтап қана әрі адиабаттық, әрі квазистатикалық дей аламыз
Сурет 2. Қайтарымды процесс 2 суретте қайтарымды процесс кӛрсетілген
Осындай айырмашылыққа қарамастан, (P,V), (T,S) жүйелерде осы процесстерді айналымды (круговой) диаграммамен қарастыруға болады
Сондықтан келесі формула орынды 𝑄 1 =𝑄 2 +𝐴 пол +𝑄 3 +𝑄 4
Термодинамиканың осы заңынан Клаузиустың және
Сурет 2. Термодинамиканың екінші заңы бойынша мүмкін процесс
Сонда жасалған жұмыс
Термодинамиканың екінші заңынан, екінші бастауынан
Екінші машина салқындатқышқа кӛбірек жылу береді
- 📁 ЗАДАНИЯ
© ООО «Знанио»
С вами с 2009 года.
