Курс лекций по геодезии и картографии

Курс лекций по ОП 08

«Основы геодезии и картографии»

Министерство образования науки и молодежной политики Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Пашковский сельскохозяйственный колледж»

(ГБПОУ КК «ПСХК»)

КУРС ЛЕКЦИЙ

по ОП 08 «Основы геодезии и картографии»

Специальность– 21.02.04 «Землеустройство (базовая подготовка)

Преподаватель: Десятникова О.В.

Краснодар – 2023 г.

СОДЕРЖАНИЕ

Пояснительная записка

       Данный курс лекций рекомендован как для самостоятельного изучения, так и на уроках учебной общепрофессиональной дисциплины «Основы геодезии и картографии» студентами специальности 21.02.04 «Землеустройство» базового уровня подготовки очной формы обучения.

         Методическая разработка составлена в соответствии с рабочей программой по ОП 08 «Основы геодезии и картографии», утвержденной в 2016 г.

    Материалы данной разработки способствуют реализации  общих и профессиональных компетенций:

·        ПК 1.1 Выполнять полевые геодезические работы на производственном участке

·        ПК 1.2 Обрабатывать результаты полевых измерений

·        ПК 1.3 Составлять и оформлять планово-картографические материалы

·        ПК 1.4 Проводить геодезические работы при съемке больших территорий

·        ПК 1.5 Подготавливать материалы аэро- и космических съемок для использования при проведении изыскательских и землеустроительных работ.

·        ПК 2.5 Осуществлять перенесение проектов землеустройства в натуру, для организации и устройства территорий различного назначения.

·        ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

·        ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

·        ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.

·        ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

·        ОК 5. Использовать информационно-коммуникационные технологии для использования профессиональной деятельности.

·        ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.

·        ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполнения заданий.

·        ОК 8. Самостоятельно определить задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

·        ОК 9. Быть готовым к смене технологий в профессиональной деятельности.

        Методическая разработка составлена на основании опыта преподавания с учётом рекомендаций по оформлению методических разработок.

     Создание данного курса лекций вызвана трудностью усвоения студентами данного материала из-за большого объема информации в учебной литературе и для подготовки к экзамену.

         Предлагаемый  материал  может быть использован  как дополнительный  к учебнику для более качественного усвоения информации по данной теме.

      Курс лекций по ОП 08 «Основы геодезии и картографии» имеет следующую структуру:

Лекция 1. Введение.

Основные сведения о геодезии и картографии. Краткие исторические сведения. Связь с другими дисциплинами и модулями. Значение геодезии и картографии в землеустройстве.

Геодезия занимается изучением Земли в геометрическом отно­шении. Название произошло от греческих слов: гео — Земля и дазоман — делю, т. е. землеразделение. Отсюда видно, что геодезия очень близка к геометрии — науке о землеизмерении. Обе эти науки зародились в глубокой древности. С развитием человеческого общества геометрия стала заниматься изучением пространственных форм, а практическая ее часть в приложении к вопросам измере­ния на Земле получила название геодезии.

Современная геодезия является многогранной наукой, решающей слож­ные научные, научно-технические и инженерные задачи путем спе­циальных измерений, выполняемых при помощи геодезических и дру­гих приборов, и последующей математической и графической обработки их результатов.

Геодезия тесно связана с картографией — наукой о составлении карт. Геодезические материалы служат основой для составления карт.

Задачей геодезии является изучение деталей земной поверхно­сти. В результате изучения получают планы, карты и числовые характеристики, относящиеся к Земле в целом и отдельным участ­кам, линиям и точкам на ней.

В геодезии изучаются способы и инструменты, применяемые при измерении углов и линий, при вычислительной обработке ре­зультатов измерений и при составлении планов, карт, профилей.

Геодезические работы по содержанию и характеру подразделя­ются на две стадии: 1) полевые измерительные работы с применением современной геодезической техники; 2) вычислительная обра­ботка результатов измерений, графическое составление и оформле­ние планов и карт.

С развитием человеческого общества, с повышением уровня нау­ки и техники меняется и содержание геодезии. В процессе своего раз­вития геодезия разделилась на ряд самостоятельных научных и науч­но-технических дисциплин.

Исключительно большое значение планово-картографический материал имеет в сельском хозяйстве. Землеустроительные органы занимаются проблемой рационального использования земли. Ведется систематический учет всех категорий земель, составляются земле­устроительные проекты, где получают отражение границы колхозов и совхозов, бригад и отделений, полей севооборотов, населенные пункты, дороги, реки, леса и др. Перед сельским хозяйством стоят задачи орошения, осушения земельных участков и проведение ме­роприятий по борьбе с эрозией почв. Все эти вопросы можно решать только с помощью картографо-геодезических материалов. Для решения многих вопросов агротехники нужны планы и карты с отображением почвы, рельефа, растительности, водоемов и др.

Методы изучения  Земли в целом как планеты в значительной степени отличаются от методов изучения отдельных участков на земной поверхности. Земля в целом представляет сферическое те­ло. Сведения, относящиеся к изучению формы и размеров Земли в целом, а также больших территорий с учетом сферичности, сос­тавляют науку, называемую высшей геодезией.)

В высшей геодезии изучают вопросы построения опорных гео­дезических сетей с определением положения точек. Результаты ма­тематической обработки опорных геодезических сетей необходимы для инженерной геодезии и картографирования больших террито­рий. Точные геодезические измерения применяются для изучения движения земной коры, происходящего от внутренних сил Земли. Знание формы и размеров Земли необходимы для геофизики, аст­рономии и для изучения космического пространства.

Задачей космической геодезии является определение положения опорных точек при помощи искусственных спутников Земли с при­менением радиотехники.

Геодезия имеет связь с другими науками. Математика исполь­зуется для теоретического обоснования и обработки результатов измерений, физика, механика — для создания приборов. География помогает понять некоторые закономерности в природе и правильно отобразить их на плане. Планы и карты должны быть ориентиро­ваны относительно стран света, поэтому геодезия пользуется аст­рономическими методами определения углов ориентирования линий местности.

Землеустройство, включающее систему государственных мероприятий, направленных на организацию наиболее полного, рационального и эффектив­ного использования земель, повышение культуры земледелия и охрану земель, имеет тесную связь с геодезией. В землеустроительные работы входит: обра­зование новых, а также упорядочение существующих землепользовании с устра­нением чересполосицы и других неудобств в расположении земель, уточне­ние и изменение границ землепользовании на основе схем районной планировки; внутрихозяйственная организация территории колхозов, совхозов и других сельскохозяйственных предприятий, организаций и учреждений с введением экономически обоснованных севооборотов на пахотных землях и устрой­ством всех других сельскохозяйственных угодий (сенокосов, пастбищ, садов и др.), а также разработка мероприятий по борьбе с эрозией почв; выявление новых земель для сельскохозяйственного и иного народнохозяйственного освое­ния; отвод и изъятие земельных участков; установление и изменение городской черты, поселковой черты и черты сельских населенных пунктов; проведение топографо-геодезических, почвенных, геоботанических и других обследова­ний и изысканий.

Для проведения землеустроительных мероприятий требуются планы, карты и профили, на основании которых определяется существующее состояние земельного фонда; затем путем экономических расчетов устанавливают потреб­ность в составе земель для тех или иных целей, после чего на планах и картах проектируют объекты землеустройства (участки, поля) и, наконец, границы спроектированных объектов переносят на местность. В этом сложном процессе землеустройства геодезические действия часто выполняют параллельно с земле­устроительными.

Геодезические работы производятся также в связи с проведением осуши­тельной или оросительной мелиорацией земель, планировкой сельских населен­ных пунктов и других мероприятий, связанных с землеустройством.

В проведении землеустроительных мероприятий под руководством земле­устроителя участвует большое число различных специалистов: геодезисты и топографы, почвоведы и геоботаники, мелиораторы и дорожники, агрономы и строители, гидрогеологи и много других, которым также необходимы планы и карты.

Большая роль принадлежит геодезии в проведении государственного земельного кадастра, направленного на организацию «эффективного использо­вания земель и их охраны, планирования народного хозяйства, размещения и специализации сельскохозяйственного производства, мелиорации земель и химизации сельского хозяйства, а также осуществления других народно­хозяйственных мероприятий, связанных с использованием земель».

Из истории развития общества известно, что понятие об изме­рениях и вычислениях возникли в глубокой древности. Археология установила, что в Египте за 4000 лет до н. э. производили изме­рение земли в районе р. Нила. Строительство канала, соединя­ющего Нил с Красным морем, относится к VI в. до н. э. Следо­вательно, тогда были известны некоторые методы съемок. В Греции ученый Эратосфен за 230 лет до н. э. определил размер земного шара. Им написана книга по геодезии и составлены карты с мери­дианами и параллелями. Птоломей (87—150 гг. н. э.) провел боль­шие работы по составлению карт Европы и Азии и применению метода проекций. Он ввел деление окружности на 360°.

В нашей стране первые письменные документы о геодезии от­носятся ко времени Киевской Руси. В летописи 996 г. имеются указания о порядке пользования землей. В 1068 г. князь Глеб измерял по льду расстояние от Тамани до Керчи. Геодезические работы XIII—XV вв. применялись при земельной переписи, где линии измерялись веревкой, а углы описывались текстом. В XVI в. границы землевладений устанавливались «землемерием». К этому времени относится появление в России первой книги по геодезии. На территории Московского государства в XVII в. было проведено описание обмера земель и составлен «Большой чертеж» с нанесе­нием рек, дорог и населенных пунктов. В XVIII в. при Петре I в Москве была организована первая геодезическая школа под на­званием «Школа математических и навигационных наук». В XIX в для создания геодезической опоры применялся метод триангуляции. Под руководством знаменитого русского геодезиста-астронома В. Струве был проложен триангуляционный ряд, кото­рый был использован для определения размеров земного эллип­соида. К началу XX в. геодезические работы в нашей стране выпол­нялись корпусом военных топографов, горным ведомством, гидро­техническим и переселенческим управлениями. В это время был выполнен большой объем геодезических работ, но они носили разобщенный характер, так как часто были подчи­нены интересам отдельных землевладельцев. После Великой Октябрьской социалистической революции со­держание геодезических работ в нашей стране значительно изме­нилось. Совет Народных Комиссаров, возглавляемый В. И. Лени­ным, высоко оценил роль геодезических работ в народном хозяй­стве страны и 15 марта 1919 г. издал декрет об организации Высшего Геодезического Управления. Этим декретом на Высшее Геодезиче­ское Управление были возложены большие функции: а) объединять геодезическую деятельность всех учреждений республики; б) производить основные геодезические работы; в) про­изводить топографические съемки на всей территории республики; г) устранять параллелизм в геодезических работах, систематизи­ровать топографические материалы учреждений и составлять карты; д) разрабатывать правила и инструкции для выпол нения картографо-геодезических работ; е) изготовлять и снабжать учрежде­ния геодезическими приборами; ж) организовывать научные работы по геодезии, астрономии, картографии, инструментоведению и гото­вить кадры специалистов; з) входить в сношения с геодезическими организациями иностранных государств и т. д. В настоящее время наша промышленность выпускает сложные и высокоточные геодезические, астрономические, аэрофотосъемочные и радиоизмерительные приборы. В нашей стране работали и работает много видных ученых. Проф. Ф. Н. Красовский (1878—1948 гг.) научно обосновал мето­дику создания опорных геодезических сетей и определил новые размеры эллипсоида. Проф. В. В. Данилов (1889—1953 гг.) теоре­тически обосновал метод параллактической полигонометрии. Боль­шой вклад в геодезическую науку внесли ученые-геодезисты В. В. По­пов, Н. Г. Келль, А. С. Чеботарев и др. В настоящее время успешно продолжают научные исследования А. А. Изотов, П. С. Закатов, А. В. Маслов, Н. Г. Видуев, Л. С. Хренов, В. Н. Гань-шин и другие.

Основные сведения о картографии. Краткие исторические сведения.

Картография – это наука, рассматривающая методы составления, издания и использования разнообразных карт. Создание карт основано на использовании и обобщении геодезических и топографических материалов, крупномасштабных планов, материалов аэрофотосъемки и космической съемки.

В результате изучения картографии  получают информацию о классификации карт и других картографических произведений, основных элементах карты (математической основе, картографическом изображении, элементах дополнительных характеристик и оснащении), способах картографического изображения, элементах подробного изображения поверхности Земли, способах создания топографических и специальных карт, сущности генерализации, основных этапах создания и издания различных карт, методах цифрового картографирования, современных тенденциях развития картографии.

Самые древние карты, найденные на территории Греции, датируются примерно 1500 г. до н.э. Это фрески, на них изображена долина реки с богатой экзотической растительностью, в зарослях которой бродят дикие звери, и плывущая по реке флотилия.

Первым «научил» карту говорить языком масштаба Анаксимандр, греческий ученый, живший в VII – VI вв. до н.э. Им была создана карта мира с использованием масштаба, в центре которой была помещена Греция.

Карты местности выполнялись и в то время на носителях, обеспечивающих длительное их использование: поверхность камня, костяные пластинки, дерево, береста.

Современные карты представляют собой весьма точные изображения поверхности Земли, обеспечивающие решение многих задач в различных областях народного хозяйства

Контрольные вопросы:

1.      Что такое геодезия и какие вопросы она решает?

2.      Как развивалась геодезия и картография?

3.      Каково значение геодезии и картографии в землеустройстве?

4.      С какими науками связана геодезия?

Тема 1.1 Определение положения точек на земной поверхности.

Лекция 2. Понятие о форме и размерах Земли. Методы проекций в геодезии.

Понятие о форме и размерах Земли.

В геодезии для обозначения формы земной поверхности используют термин «фигура Земли».

Знание фигуры и размеров Земли необходимо во многих областях и прежде всего для определения положения объектов на земной поверхности и правильного её изображения в виде карт, планов и цифровых моделей местности.

Физическая поверхность Земли состоит из подводной (70,8 %) и надводной (29,2 %) частей. Подводная поверхность включает в себя систему срединно-океанических хребтов, подводные вулканы, океанические желоба, подводные каньоны, океанические плато и абиссальные равнины. Надводная часть земной поверхности также характеризуется многообразием форм. С течением времени поверхность Земли из-за тектонических процессов и эрозии постоянно изменяется.

Рис. 1. Фигура Земли (вид из космоса)

Представление о фигуре Земли (рис. 1) в целом можно получить, вообразив, что вся планета ограничена мысленно продолженной поверхностью океанов в спокойном состоянии.

Уровенных поверхностей, огибающих Землю, можно вообразить множество. Та из них, что совпадает со средним уровнем воды океанов в спокойном состоянии, т.е. в момент полного равновесия всей массы находящейся в ней воды под влиянием силы тяжести, называется основной уровенной поверхностью Земли.

В геодезии, как и в любой другой науке, одним из основополагающих принципов является принцип перехода от общего к частному. Исходя из него, для решения научных и инженерных задач по изучению физической поверхности Земли, а также других геодезических задач, сначала необходимо определиться с математической моделью поверхности Земли.

Математическая поверхность Земли

           Рассмотрим любую материальную точку А на физической поверхности Земли

(рис. 2).

На эту точку оказывают влияние две силы: сила притяжения F_п, направленная к центру Земли, и центробежная сила вращения Земли вокруг своей оси F_ц, направленная от оси вращения по перпендикуляру. Равнодействующая этих сил называется силой тяжести F_т.

В любой точке земной поверхности направление силы тяжести, называемое ещё вертикальной или отвесной линией, можно легко и просто определить с помощью уровня или отвеса. Оно играет очень большую роль в геодезии. По направлению силы тяжести ориентируется одна из осей пространственной системы координат.

Если через точку А построить замкнутую поверхность, которая в каждой своей точке будет перпендикулярна отвесной линии (направлению силы тяжести), то данную поверхность можно принять в качестве математической при решении некоторых частных задач в геодезии. Такая поверхность получила название уровенной или горизонтальной. Её недостаток в том, что она содержит элемент неопределенности, т.е. через любую точку можно провести свою уровенную поверхность, и таких поверхностей будет бесчисленное множество.

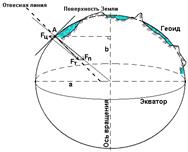
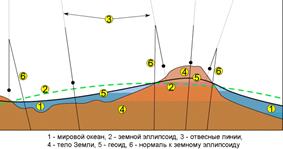
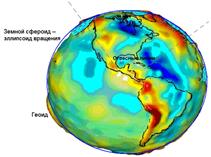
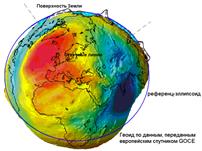
Рис. 2. Моделирование фигуры Земли

Для устранения этой неопределенности при решении общих геодезических задач принимается так называемая общая математическая поверхность, т.е. уровенная поверхность, которая в каждой своей точке совпадает со средним уровнем морей и океанов в момент полного равновесия всей массы воды под влиянием силы тяжести. Такая поверхность носит название общей фигуры Земли или поверхности геоида.

Геоид – выпуклая замкнутая поверхность, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии и перпендикулярная к направлению силы тяжести в любой её точке (см. рис. 2).

Фигура геоида зависит от распределения масс и плотностей в теле Земли. Из-за неравномерного распределения масс внутри Земли геоид не имеет правильной геометрической формы, и в математическом отношении его поверхность характеризуется слишком большой сложностью. Поэтому там, где это допустимо, поверхность геоида заменяется приближенными математическими моделями, в качестве которых принимается в одних случаях земной сфероид, в других – земной шар, а при топографическом изучении незначительных по размеру территорий – горизонтальная плоскость, т.е. плоскость, перпендикулярная к вертикальной линии в данной точке.

Земной сфероид – эллипсоид вращения получается вращением эллипса вокруг его малой оси b (см. рис. 3), совпадающей с осью вращения Земли, причем центр эллипсоида совмещается с центром Земли.

Размеры эллипсоида подбирают при условии наилучшего совпадения поверхности эллипсоида и геоида в целом (общеземной эллипсоид) или отдельных его частей (референц-эллипсоид).

Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимают для обработки геодезических измерений законодательно.

Наиболее удачная математическая модель Земли в виде референц-эллипсоида была предложена проф. Ф. Н. Красовским с большой полуосью a=6378245 м, малой – b=6356863 м  и  коэффициентом сжатия у полюсов a = (a-b)/a = 1/298.3 ~ 1/300. Отклонения эллипсоида Красовского от геоида на территории СНГ не превышают 150 м.

Постановлением Совета Министров СССР № 760 от 7 апреля 1946 года эллипсоид Красовского принят для территории нашей страны в качестве математической поверхности Земли.

В инженерной геодезии для практических расчетов за математическую поверхность Земли принимают шар со средним радиусом R=6371.11 км. Объем шара равен объему земного эллипсоида.

Метод проекций в геодезии

Пусть многоугольник ABCDE представляет собой часть земной поверхности. Возьмем плоскость PQ и опустим из каждой вершины многоугольника перпендикуляры на эту плос­кость. Основания этих перпендикуляров обозначим соответственно через а, Ь, с, d, е. Полученные на плоскости точки называются ортогональными (прямоугольными) проекциями точек простран­ства; линии ab, Ьс, ... называются ортогональными проекциями линий АВ, ВС, ..., а углы abc, bed, ... — ортогональными проек­циями углов ABC, BCD, ... Плоский многоугольник abede явля­ется ортогональной проекцией пространственного многоуголь­ника ABCDE.

Другая имеющая важное значение в геодезии проекция назы­вается центральной. Суть ее заключается в следующем. Возьмем произвольную точку О  и соединим ее со всеми верши­нами многоугольника ABCDE, находящегося на земной поверх­ности. Полученные в пересечении с горизонтальной плоскостью PQ точки а, Ь, с, d, е и будут центральными проекциями точек А, В, С, D, Е.

Плоский многоугольник abede называется центральной проек­цией многоугольника ABCDE.

Лекция 3. Системы координат и высот, применяемые в геодезии.

Проектирование земной поверхности. Системы координат.

Топографическое изучение земной поверхности заключается в определении положения ситуации и рельефа относительно математической поверхности Земли, т.е. в определении пространственных координат характерных точек, необходимых и достаточных для моделирования местности. Модель местности может быть представлена в виде геодезических чертежей, изготовление которых называют картографированием, и аналитически – в виде совокупности координат характерных точек. Для построения моделей местности в геодезии применяют метод проекций и различные системы координат.

Метод горизонтальной проекции заключается в том, что изучаемые точки (A, B, C, D, E) местности с помощью вертикальных (отвесных) линии проектируются на уровенную поверхность У (рис. 3), в результате чего получают горизонтальные проекции этих точек (a, b, c, d, e). Отрезки Аa, Bb, Cc, Dd, Ee называются высотами точек, а численные их значения – отметками.

Высота точки является одной из её пространственных координат. Отметка называется абсолютной, если в качестве уровенной поверхности принимается геоид, и относительной или условной, если для этого принимается произвольная уровенная поверхность.

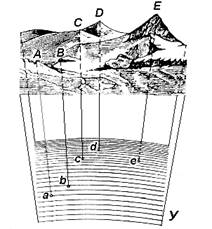
Рис. 3. Проектирование точек местности на уровенную поверхность Земли.

Две другие недостающие координаты точки определяются с помощью системы координат, построенной на математической поверхности Земли (рис. 4).

Через любую точку поверхности референц-эллипсоида можно провести две взаимно перпендикулярные плоскости:

плоскость геодезического меридиана – плоскость, проходящая через ось вращения Земли PP'; плоскость геодезической широты, которая перпендикулярна плоскости геодезического меридиана.

Следы сечения поверхности референц-эллипсоида этими плоскостями называют меридианом (М) и параллелью.

Меридиан, проходящий через астрономическую обсерваторию в Гринвиче, называется начальным или нулевым (М₀).

Параллель, плоскость которой проходит через центр Земли O, называется экватором (Э).

Плоскость, проходящая через центр Земли O перпендикулярно к её оси вращения PP', называется экваториальной.

Основой для всех систем координат являются плоскости меридиана и экватора.

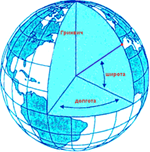
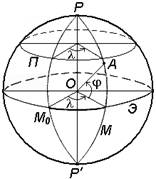
Рис. 4. Система географических координат.

Системы координат подразделяются на угловые, линейные и линейно – угловые.

Примером угловых координат являются географические координаты (рис.4): широта  и долгота. Вдоль соответствующих параллели и меридиана широта и долгота точек постоянны.

В геодезии применяются следующие системы координат:

геодезические;

астрономические;

географические;

плоские прямоугольные геодезические (зональные);

полярные;

местные.

Геодезические координаты

Геодезические координаты определяют положение точки земной поверхности на референц-эллипсоиде (рис.5).

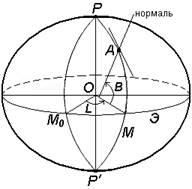
Рис. 5. Система геодезических координат.

Геодезическая широта  B – угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью его экватора. Широта отсчитывается от экватора к северу или югу от 0° до 90° и соответственно называется северной или южной широтой.

Геодезическая долгота L – двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического Гринвичского меридиана.

Долготы точек, расположенных к востоку от начального меридиана, называются восточными, а к западу – западными.

Астрономические координаты

Астрономическая широта и долгота определяют положение точки земной поверхности относительно экваториальной плоскости и плоскости начального астрономического меридиана (рис.6).

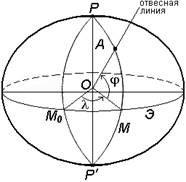
Рис. 6. Система астрономических координат

Астрономическая  широта  – угол, образованный отвесной линией в данной точке и экваториальной плоскостью.

Астрономическая  долгота  – двугранный угол между плоскостями астрономического меридиана данной точки и начального астрономического меридиана.

Плоскостью астрономического меридиана является плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.

Астрономическая широта и долгота определяются астрономическими наблюдениями.

Геодезические и астрономические координаты отличаются (имеют расхождение) из-за отклонения отвесной линии от нормали к поверхности эллипсоида. При составлении географических карт этим отклонением пренебрегают.

Географические координаты

Географические координаты – величины, обобщающие две системы координат: геодезическую и астрономическую, используют в тех случаях, когда отклонение отвесных линий от нормали к поверхности не учитывается (рис.7).

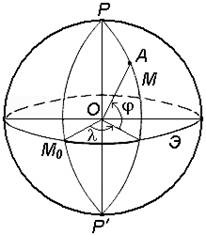
Рис. 7. Система географических координат

Географическая широта  – угол, образованный отвесной линией в данной точке и экваториальной плоскостью.

Географическая долгота  – двугранный угол между плоскостями меридиана данной точки с плоскостью начального меридиана.

Плоские прямоугольные геодезические координаты (зональные).

При решении инженерно-геодезических задач в основном применяют плоскую прямоугольную геодезическую и полярную системы координат.

Для определения положения точек в плоской прямоугольной геодезической системе координат используют горизонтальную координатную плоскость ХОУ (рис.8), образованную двумя взаимно перпендикулярными прямыми. Одну из них принимают за ось абсцисс X, другую – за ось ординат Y, точку пересечения осей О – за начало координат.

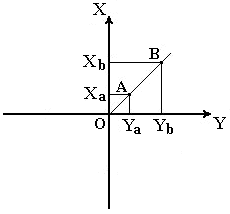
Рис. 8. Плоская прямоугольная система координат

Изучаемые точки проектируют с математической поверхности Земли на координатную плоскость ХОУ. Так как сферическая поверхность не может быть спроектирована на плоскость без искажений (без разрывов и складок), то при построении плоской проекции математической поверхности Земли принимается неизбежность данных искажений, но при этом их величины должным образом ограничивают. Для этого применяется равноугольная картографическая проекция Гаусса – Крюгера (проекция названа по имени немецких ученых, предложивших данную проекцию и разработавших формулы для её применения в геодезии), в которой математическая поверхность Земли проектируется на плоскость по участкам – зонам, на которые вся земная поверхность делится меридианами через 6° или 3°, начиная с начального меридиана (рис. 9).

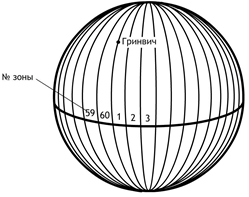
Рис. 9. Деление математической поверхности Земли на шестиградусные зоны

В пределах каждой зоны строится своя прямоугольная система координат. С этой целью все точки данной зоны проецируются на поверхность цилиндра (рис. 10, а), ось которого находится в плоскости экватора Земли, а его поверхность касается поверхности Земли вдоль среднего меридиана зоны, называемого осевым. При этом соблюдается условие сохранения подобия фигур на земле и в проекции при малых размерах этих фигур.

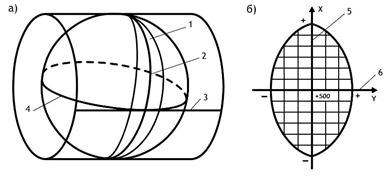
Рис. 10. Равноугольная картографическая проекция Гаусса – Крюгера (а) и  зональная система координат (б):

1 – зона, 2 – осевой (средний) меридиан зоны, 3 – проекция экватора на поверхность цилиндра, 4 – экватор,

5 – ось абсцисс – проекция осевого меридиана, 6 – ось ординат – проекция экватора

После проектирования точек зоны на цилиндр, он развертывается на плоскость, на которой изображение проекции осевого меридиана и соответствующего участка экватора будет представлена в виде двух взаимно перпендикулярных прямых (рис. 10, б). Точка пересечения их принимается за начало зональной плоской прямоугольной системы координат, изображение северного направления осевого меридиана – за положительную ось абсцисс, а изображение восточного направления экватора – за положительное направление оси ординат.

Для всех точек на территории нашей страны абсциссы имеют положительное значение. Чтобы ординаты точек также были только положительными, в каждой зоне ординату начала координат принимают равной 500 км (рис. 10, б). Таким образом, точки, расположенные к западу от осевого меридиана, имеют ординаты меньше 500 км, а к востоку – больше 500 км. Эти ординаты называют преобразованными.

Искажения длин линий в данной проекции увеличиваются по мере удаления от осевого меридиана к краям зоны. На границах зон в пределах широт от 30° до 70° относительные ошибки, происходящие от искажения длин линий в этой проекции, колеблются от 1:1000 до 1:6000. Когда такие ошибки недопустимы, прибегают к трехградусным зонам.

На картах, составленных в равноугольной картографической проекции Гаусса – Крюгера, искажения длин в различных точках проекции различны, но по разным направлениям, выходящим из одной и той же точки, эти искажения будут одинаковы. Круг весьма малого радиуса, взятый на уровенной поверхности, изобразится в этой проекции тоже кругом. Поэтому говорят, что рассматриваемая проекция конформна, т. е. сохраняет подобие фигур на сфере и в проекции при весьма малых размерах этих фигур. Таким образом, изображения контуров земной поверхности в этой проекции весьма близки к тем, которые получаются.

Четверти прямоугольной системы координат нумеруются. Их счет идет по ходу стрелки от положительного направления оси абсцисс (рис.11).

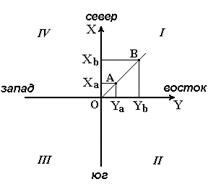
Рис. 11. Четверти прямоугольной системы координат

Если за начало плоской прямоугольной системы координат принять произвольную точку, то она будет называться относительной или условной.

Полярные координаты

При выполнении съемочных и разбивочных геодезических работ часто применяют полярную систему координат (рис.12). Она состоит из полюса О и полярной оси ОР, в качестве которых принимается прямая с известным началом и направлением.

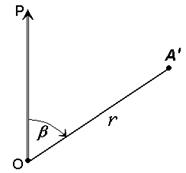
Рис. 12. Полярная система координат

Для определения положения точек в данной системе используют линейно-угловые координаты: угол β, отсчитываемый по часовой стрелке от полярной оси ОР до направления на горизонтальную проекцию точки А', и полярное расстояние r от полюса системы О до проекции А'.

Системы высот

Высота точки является третьей координатой, определяющей её положение в пространстве.

В геодезии для определения отметок точек применяются следующие системы высот (рис.13):

ортометрическая (абсолютная);

геодезическая;

нормальная (обобщенная);

относительная (условная).

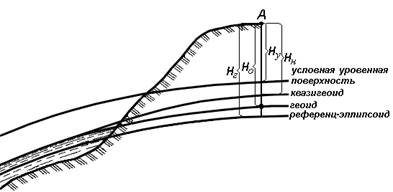
Рис. 13. Системы высот в геодезии

Ортометрическая (абсолютная) высота H_о – расстояние, отсчитываемое по направлению отвесной линии от поверхности геоида до данной точки.

Геодезическая высота H_г – расстояние, отсчитываемое по направлению нормали от поверхности референц-эллипсоида до данной точки.

В нашей стране все высоты реперов государственной нивелирной сети определены в нормальной системе высот. Это связано с тем, что положение геоида под материками определить сложно. Поэтому с конца 40-х годов в СССР было принято решение не применять ортометрическую систему высот.

В нормальной системе высот отметка точки H_н отсчитывается по направлению отвесной линии от поверхности квазигеоида, близкой к поверхности геоида. Отличие реального среднего уровня моря от геоида может достигать 1 м.

Квазигеоид («якобы геоид») – фигура, предложенная в 1950-х г.г. советским учёным М.С. Молоденским в качестве строгого решения задачи определения фигуры Земли путем тщательных измерений гравитационного поля Земли. Квазигеоид определяется по измеренным значениям потенциалов силы тяжести согласно положениям теории М.С. Молоденского.

В нашей стране все высоты реперов государственной нивелирной сети определены в нормальной системе высот. Это связано с тем, что положение геоида под материками определить сложно. Поэтому с конца 40-х годов в СССР было принято решение не применять ортометрическую систему высот.

В России абсолютные высоты точек определяются в Балтийской системе высот (БСВ) относительно нуля Кронштадтского футштока – горизонтальной черты на медной пластине, прикрепленной к устою моста через обводной канал в г. Кронштадте.

 Относительная высота H_у – измеряется от любой другой поверхности, а не от основной уровенной поверхности.

Местная система высот – Тихоокеанская,  её уровенная поверхность ниже нуля Кронштадтского футштока на 1873 мм.

Контрольные вопросы:

1.      Что такое физическая и уровенная поверхность Земли?

2.      Что такое геоид?

3.      Что принимается за математическую поверхность Земли?

4.      Что является фигурой Земли?

5.      Назовите размеры эллипсоида Ф.Н. Красовского?

6.      Что называется геодезической широтой и долготой?

7.      Какие системы координат применяются в геодезии?

8.      Поясните суть зональной системы прямоугольных координат?

9.      Что называется абсолютной и условной высотой точки?

10.  Что называется отметкой точки на земной поверхности?

Тема 1.2 Понятие о плане, карте и масштабе.

Лекция 4. Геодезические планы. Классификация карт. Понятие о чертежах и профилях.

Чтобы спроектировать линию местности на горизонтальную плоскость, нужно определить её горизонтальное проложение (проекцию линии на горизонтальную плоскость) и уменьшить его до определенного масштаба. Для проектирования на горизонтальную плоскость какого-либо многоугольника (рис. 14) измеряют расстояния между его вершинами и горизонтальные проекции его углов.

Совокупность линейных и угловых измерений на земной поверхности называется геодезической съемкой. По результатам геодезической съемки составляют план или карту.

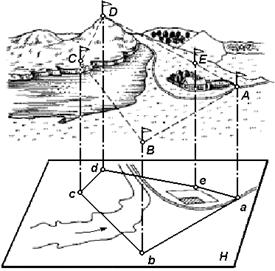
Рис. 14. Проектирование участка земной поверхности на горизонтальную плоскость

План – чертеж, на котором в уменьшенном и подобном виде изображается горизонтальная проекция небольшого участка местности.

Карта – уменьшенное и искаженное изображение картографической проекции значительной части или всей земной поверхности, построенное по определенным математическим законам, учитывающим влияние кривизны Земли.

Таким образом, и план, и карта – это уменьшенные изображения земной поверхности на плоскости. Различие между ними состоит в том, что при составлении карты проектирование производят с искажениями поверхности за счет влияния кривизны Земли, на плане изображение получают практически без искажений.

В зависимости от назначения планы и карты могут быть контурные и топографические. На контурных планах и картах условными знаками изображают ситуацию, т.е. только контуры (очертания) горизонтальных проекций местных предметов (дорог, строений, пашен, лугов, лесов и т.п.).

На топографических картах и планах кроме ситуации изображают ещё рельеф местности.

Для проектирования железных, шоссейных дорог, каналов, трасс, водопроводов и других сооружений необходимо иметь вертикальный разрез или профиль местности.

Профилем местности называется чертеж, на котором изображается в уменьшенном виде сечение вертикальной плоскостью поверхности Земли по заданному направлению.

Как правило, разрез местности (рис. 15, а) представляет собой кривую линию ABC...G. На профиле (рис. 15, б) она строится в виде ломаной линии abc...g. Уровенную поверхность изображают прямой линией. Для большей наглядности вертикальные отрезки (высоты, превышения) делают крупнее, чем горизонтальные (расстояния между точками).

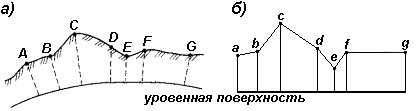
Рис. 15. Вертикальный разрез (а) и профиль (б) местности

Лекция 5. Элементы содержания топографических карт и планов. Особенности содержания сельскохозяйственных карт.

Элементы содержания топографических карт и планов.

Карта или план состоит из зарамочного оформления, рамки и внутреннего содержания.

Зарамочное оформление включает: номенклатуру (шифр) листа, год издания, масштаб, сечение рельефа, метод съемки, системы координат и высот, величины сближения меридианов и склонения магнитной стрелки.

Рамка карты (плана)содержит координаты углов рамки в географической системе и выходы километровой сетки в прямоугольной системе координат. На планах подписываются углы рамки трапеции только в прямоугольной системе координат.

Содержание карты (плана)состоит в изображении всех элементов земной поверхности (контура, предметы, дороги, водоемы, растительный покров, сооружения, коммуникации и т.д.) – ситуации с использованием масштабных и немасштабных условных знаков, пояснительных надписей, цветовой окраски, принятые едиными для данного государства и неровностей земной поверхности – рельефа, изображенного отметками и горизонталями. Подробность изображения ситуации зависит от масштаба карты или плана (чем крупнее масштаб, тем подробнее карта или план), а рельефа- от сечения (чем меньше сечение, тем подробнее изображен рельеф).

Особенности содержания сельскохозяйственных карт.

Сельскохозяйственные карты — это географические карты, характеризующие сельское хозяйство, условия и факторы его развития. Они помогают правильно использовать землю. По своему содержанию карты очень разнообразны и могут быть разделены на две большие группы.

К первой относятся карты земельных фондов и землепользований, материально-технической базы сельского хозяйства и трудовых ресурсов.

Карты земельного фонда дают информацию о том, в чьем пользовании находятся земли: сельскохозяйственных, промышленных предприятий или населенных пунктов и государственного лесного фонда. Карты материально-технической базы включают карты основных производственных фондов (машины, хозяйственные постройки, продуктивный скот, многолетние насаждения), а также карты механизации и электрификации сельскохозяйственного производства, которые показывают, в какой степени обеспечено сельское хозяйство электроэнергией и машинами. На картах трудовых ресурсов отражается обеспеченность сельскохозяйственного производства рабочей силой.

Вторую группу карт составляют карты отраслей сельского хозяйства растениеводства и животноводства и сельскохозяйственного районирования.

Наиболее широко распространены карты размещения и урожайности сельскохозяйственных культур. На картах животноводства показывается размещение поголовья различных видов скота: овец и коз, свиней, лошадей, крупного рогатого скота.

Лекция 6. Условные знаки топографических планов и карт.

Условные знаки топографических планов и карт.

Для обеспечения требования наглядности топографических материалов и понимания содержания планов и карт разработана специальная система графического обозначения предметов местности, которая называется условными знаками.Условные знаки подразделяют на площадные, линейные, внемасштабные, пояснительные и специальные.

П л о щ а д н ы е (контурные или масштабные) знаки применяют для заполнения контуров природных и сельскохозяйственных угодий, длина и ширина которых выражается в масштабе карты. Границы контуров показывают точечным пунктиром, внутри которых изображается условный знак, напоминающий предмет на данной площади. Например, лес изображается кружками, пески – точками и т. д.

Л и н е й н ы м и условными знаками показывают объекты линейного характера (дороги, реки, ЛЭП и др.), длина которых выражается, а ширина не выражается в масштабе карты. У линейных знаков приводятся различные числительные характеристики, дополняющие сведения о предмете. Например, на шоссе показаны ширина проезжей части и общая ширина дороги.

В н е м а с ш т а б н ы е условные знаки служат для изображения объектов, размеры которых не выражаются в масштабе карты (мосты, колодцы, километровые столбы и т. д.).

П о я с н и т е л ь н ы е условные знаки представляют собой подписи, дающие характеристики и названия объектов, например длину и ширину мостов, породу лесных насаждений и др. Эти знаки проставляют на основных площадных, линейных и внемасштабных условных знаках.

С п е ц и а л ь н ы е условные знаки применяют соответствующие ведомства при составлении специальных карт и планов этой отрасли, например трубопроводы коммуникаций (теплотрасса, водопровод и т. д.).

Кроме условных знаков для большей наглядности изображения различных элементов топографических карт используют цвет:

- для рек, озер, каналов, заболоченных участков – синий;

- для лесов и садов – зеленый;

- шоссейных дорог – красный;

- железные дороги и остальная ситуация – черный;

- коричневым цветом показываются горизонтали, характеризующие рельеф местности.

Помимо цветов используются также тип шрифта, толщина букв, их высота и наклон при обозначении. Условные знаки для разных масштабов сведены в специальные сборники, издаваемые службами геодезии и картографии. Они обязательны для всех ведомств и организаций, занимающихся составлением планов, карт, топографической съемкой местности.

Знание условных знаков необходимо для того, чтобы понимать содержание топографических материалов, уметь их “читать” и для получения нужных сведений. Для лучшего ознакомления с условными знаками на учебных топографических картах приведены основные их образцы.

         Лекция 7. Масштабы и их точность. Виды масштабов.

Масштабом называется отношение длины линии на плане (профиле) к соответствующей проекции этой линии на местно­сти. Следовательно, масштаб представляет собой правильную дробь. Для удобства использования и сравнения все масштабы имеют однообразный вид: числителем дроби всегда является единица; при этом знаменатель непосредственно выражает степень умень­шения. Такой масштаб называется числовым. Наприме 1/500, 1/1000, 1/10000, 1/50000 и т.д.

Числовой масштаб дает общую характеристику степени умень­шения и не всегда удобен на практике. Для построения планов или определения длины отрезков, взятых с плана, применяют графические масштабы: линейный и поперечный.

Линейный масштаб представляет собой шкалу с делени­ями, соответствующими данному числовому масштабу.

Для построения линейного масштаба (рис. 3.1) на прямой не­сколько раз откладывают один и тот же отрезок, называемый основанием масштаба. Крайний левый отрезок делят на 10 равных частей. Тогда отрезки, отложенные от нулевой точки вправо, на­пример в масштабе 1:10000, представляют на местности 100, 200, 300, 400 и 500 м, а влево — 10, 20, 30, ..., 100 м. Если отрезок линии на плане оказался равным cd (см. рис. 3.1), то на местности ему соответствует отрезок линии длиной 240 м. Наименьший от­резок в таком масштабе соответствует 10 м на местности.

Для более точного построения плана или определения длин отрезков пользуются поперечным масштабом (рис. 3.2). За основание такого масштаба обычно принимают отрезок АВ - 2 см и делят его на 10 равных частей. Для этого под произвольным углом к основанию проводят прямую AF и на ней от точки А от­кладывают 10 произвольных, но равных частей; соединив точки В и F, проводят через все точки линии AF прямые, параллельные BF, которые и разделят основание на 10 равных частей. Далее, на линии АС, перпендикулярной АВ, откладывают 10 произвольных, но равных между собой отрезков и через полученные точки про­водят линии, параллельные АВ. Отрезки между наклонными ли­ниями, параллельными BE, равны десятым долям основания АВ, т. е. ED = АВ/10.

Отрезки, заключенные между перпендикуляром BD и наклон­ной BE, равны сотым долям основания, т. е. t = ED/10=АВ/10 * 10 = = АВ/100. Такой масштаб называют еще нормальным поперечным масштабом.

Цифры, написанные внизу масштаба, изображенного на рис. 3.2, соответствуют численному масштабу 1:10000. Тогда основание АВ для такого масштаба соответствует на местности 200 м, а наи­меньшее деление t = 200:10 -10 = 2 м. Отрезки ab и kl для данного случая будут соответствовать 468 и 356 м.

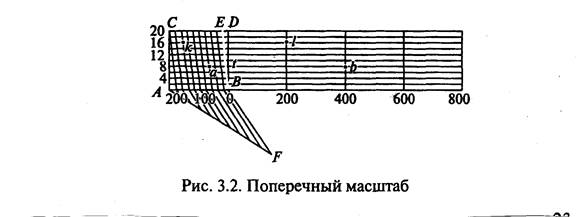
Обычно считают, что ОД мм — наименьшее расстояние, раз­личаемое непосредственно глазом. Точностью масштаба называют горизонтальное расстояние на местности, соответствующее в дан­ном масштабе 0,1 мм плана. Так, для масштабов 1:500; 1:1000; 1:5000; 1:10000 и 1:25000 точность соответственно равна 0,05; 0,1; 0,5; 1,0 и 2,5 м; отрезки, меньше указанных, не будут изобра­жаться на плане данного масштаба. Зная размеры предметов мес­тности, которые необходимо изобразить на плане, можно устано­вить соответствующий масштаб плана.

Лекция 8. Масштабный ряд, разграфка и номенклатура топографических карт и планов.

Масштабный ряд и разграфка.

Для удовлетворения потребностей хозяйства, науки и обороны страны необходимы карты различных масштабов. Для топографических карт определены стандартные масштабы – масштабный ряд.

Масштабы топографических карт

Номенклатура топографических карт и планов

Номенклатура – это система обозначения  листов карт разных масштабов.  Разграфка – система деления поверхности Земли меридианами и параллелями. Каждый лист ограничен рамкой. В основу деления карт на листы в нашей стране принята международная  разграфка карт масштаба 1:1 000 000 .  Для получения отдельных листов этой карты земной шар делится меридианами через 6^О на  колонны и параллелями через 4^О на ряды. Колонны нумеруются арабскими цифрами от 1 до 60 с запада на восток от меридиана с долготой 180^О. Ряды обозначаются заглавными буквами латинского алфавита от А,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V, начиная от экватора к северному и южному полюсу. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, на одном листе карты данного масштаба изображается каждый из 266 участков земной поверхности. При этом номенклатура отдельного листа складывается из латинской буквы, обозначающей ряд и цифры, соответствующей номеру колонны. К примеру, А-1. Номенклатура листов топографических карт и планов более крупных масштабов определяется следующим образом. Каждому листу карты масштаба 1:1 000 000 соответствуют 144 листа карты масштаба 1: 100 000, которые обозначаются арабскими цифрами  по порядку с левого верхнего угла, имеющего № 1 до правого нижнего угла, имеющего № 144. При этом номенклатура такого листа образуется прибавлением соответствующей цифры к номенклатуре листа карты 1: 1 000 000. К примеру, А-1-120. 4 листа карт масштаба 1:50 000, соответствуют одному листу карты масштаба 1: 100 000.

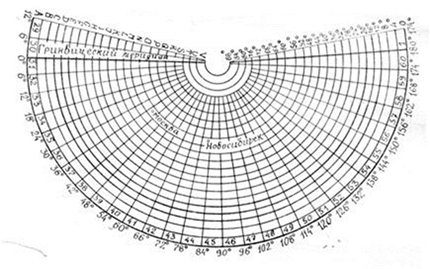
Схема разграфки и номенклатуры листов карт масштаба 1 : 1000000.

Разграфка и номенклатура топографических карт масштабов 1:100000; 1: 50000; 1: 25000 ; 1: 10000.

Каждый лист карты масштаба 1: 50 000 обозначается приписыванием к номенклатуре карты масштаба 1:100 000 одной из четырех заглавных букв русского алфавита А, Б, В, Г . К примеру, А-1-120-Б. Одному листу карты масштаба 1:50 000 соответствует 4 листа карты масштаба 1:25 000, которые обозначаются строчными буквами а,б,в,ᴦ. К примеру, А-1-120-Б-в. Четыре листа карты масштаба 1:10 000 обозначаются цифрами 1,2,3,4, приписываемыми к номенклатуре масштаба 1:25 000, А-1-120-Б-в-3. Планы и участки, площадью до 20 км² бывают разграфлены с помощью прямоугольника. В основу разграфки в данном случае положен лист плана масштаба 1:5000 с размерами рамки 40×40 см. Листы плана масштаба 1:5000 нумеруются арабским цифрами.

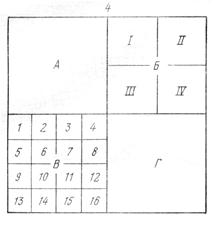
Прямоугольная разграфка и номенклатура листов планов масштабов

Лекция 9. Прямоугольные и географические координаты точек.

Координатная сетка.

Одним из элементов географической карты является сетка координатных линий. Существуют два вида координатной сетки: картографическая, образуемая линиями меридианов и параллелей, и сетка прямоугольных координат, образуемая линиями, параллельными осям координат OX и OY.

На топографических картах меридианы и параллели являются границами листа карты; в углах карты подписываются их долгота и широта. Внутри листа вычерчивается сетка прямоугольных координат в виде квадратов, называемая иногда километровой сеткой, так как на картах масштаба 1:10000 и мельче линии сетки проводятся через целое число километров.

Вертикальные линии сетки параллельны осевому меридиану зоны (оси OX); горизонтальные линии сетки параллельны оси OY. Для удобства пользования листами карт, на которых изображены граничные участки зоны, на них показывается сетка прямоугольных координат соседней зоны. Выходы линий координатной сетки соседней зоны наносятся на внешнюю сторону рамки листа карты.

Определение географических координат точек

 Для определения широты заданной точки необходимо:

одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайшую параллель;

не меняя раствор циркуля-измерителя установить его на боковую рамку с минутными и секундными делениями, одна ножка должна быть на южной параллели, а другая – между 10-секундными точками на рамке; посчитать количество минут и секунд от южной параллели до второй ножки циркуля-измерителя; добавить полученный результат к южной широте.

  Для определения долготы заданной точки необходимо:

одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайший меридиан; не меняя раствор циркуля-измерителя установить его на ближайшую горизонтальную рамку с минутными и секундными делениями, одна ножка должна быть на ближайшем меридиане, а другая – между 10-секундными точками на горизонтальной рамке;

посчитать количество минут и секунд от западного (левого) меридиана до второй ножки циркуля-измерителя; добавить полученный результат к долготе западного меридиана

Контрольные вопросы:

1.      Что называют геодезическим планом?

2.      Что такое профиль?

3.      Чем отличается карта от плана?

4.      Что такое масштаб?

5.      Какие виды масштабов бывают?

6.      Как определяется точность масштаба?

7.      Для чего нужна номенклатура карты?

8.      Какие  карты бывают?

9.      Какие бывают условные знаки?

Тема 1.3 Рельеф местности.

Лекция 10. Рельеф местности. Основные формы рельефа. Виды высот и превышений.

Рельеф – форма физической поверхности Земли, рассматриваемая по отношению к её уровенной поверхности.

Рельефом называется совокупность неровностей суши, дна океанов и морей, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития. При проектировании и строительстве железных, автомобильных и других сетей необходимо учитывать характер рельефа – горный, холмистый, равнинный и др.

Рельеф земной поверхности весьма разнообразен, но все многообразие форм рельефа для упрощения его анализа типизировано на небольшое количество основных форм (рис. 29).

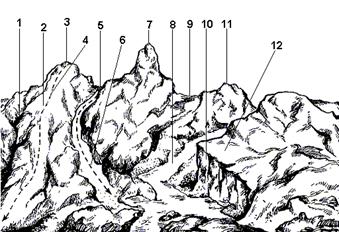
Рис. 29. Формы рельефа:

1 — лощина; 2 — хребет; 3, 7, 11 — гора; 4 — водораздел; 5, 9 — седловина; 6 — тальвег; 8 — река; 10 — обрыв; 12 — терраса

К основным формам рельефа относятся:

Гора – это возвышающаяся над окружающей местностью конусообразная форма рельефа. Наивысшая точка её называется вершиной. Вершина может быть острой – пик, или в виде площадки – плато. Боковая поверхность состоит из скатов. Линия слияния скатов с окружающей местностью называется подошвой или основанием горы.

Котловина – форма рельефа, противоположная горе, представляющая собой замкнутое углубление. Самая низкая точка её – дно. Боковая поверхность состоит из скатов; линия их слияния с окружающей местностью называется бровкой.

Хребет – это возвышенность, вытянутая и постоянно понижающаяся в каком – либо направлении. У хребта два склона; в верхней части хребта они сливаются, образуя водораздельную линию, или водораздел.

Лощина – форма рельефа, противоположная хребту и представляющая вытянутое в каком – либо направлении и открытое с одного конца постоянно понижающееся углубление. Два ската лощины; сливаясь между собой в самой низкой части её образуют водосливную линию или тальвег, по которой стекает вода, попадающая на скаты. Разновидностями лощины являются долина и овраг: первая является широкой лощиной с пологими задернованными скатами, вторая – узкая лощина с крутыми обнаженными скатами. Долина часто бывает ложем реки или ручья.

Седловина – это место, которое образуется при слиянии скатов двух соседних гор. Иногда седловина является местом слияния водоразделов двух хребтов. От седловины берут начало две лощины, распространяющиеся в противоположных направлениях. В горной местности через седловины обычно пролегают дороги или пешеходные тропы; поэтому седловины в горах называют перевалами.

Изображение рельефа на планах и картах

Для решения инженерных задач изображение рельефа должно обеспечивать: во-первых, быстрое определение с требуемой точностью высот точек местности, направления крутизны скатов и уклонов линий; во-вторых, наглядное отображение действительного ландшафта местности.

Рельеф местности на планах и картах изображают различными способами (штриховкой, пунктиром, цветной пластикой), но чаще всего с помощью горизонталей (изогипсов), числовых отметок и условных знаков.

Горизонталь на местности можно представить как след, образованный пересечением уровенной поверхности с физической поверхностью Земли. Например, если представить холм, окружённый неподвижной водой, то береговая линия воды и есть горизонталь (рис. 30). Лежащие на ней точки имеют одинаковую высоту.

Допустим, что высота уровня воды относительно уровенной поверхности 110 м (рис. 30). Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Кривая линия пересечения поверхностей воды и холма будет соответствовать горизонтали с высотой 105 м. Если последовательно снижать уровень воды по 5 м и проектировать кривые линии, образованные пересечением поверхности воды с земной поверхностью, на горизонтальную плоскость в уменьшенном виде, то получим изображение рельефа местности горизонталями на плоскости.

Таким образом кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.

Лекция 11. Свойства горизонталей. Проведение горизонталей по отметкам точек.

Свойства горизонталей и особенности их проведения:

1. Горизонталь - линия равных высот т.е. все ее точки имеют одинаковую высоту;

2. Горизонталь должна быть непрерывной плавной линией;

3. Горизонтали не могут раздваиваться  и пересекаться;

4. Расстояние между горизонталями (заложение) характеризуют крутизну ската. Чем меньше расстояние, тем круче скат;

5. Водораздельные и водосборные линии горизонтали пересекают под прямым углом;

6. В случаях, когда заложение превышает 25мм, проводят дополнительные горизонтали (полугоризонтали) в виде штриховой линии (длина штриха 5-6 мм, расстояние между штрихами 1-2 мм);

7. При окончательном оформлении плана выполняют некоторое сглаживание горизонталей в соответствии с общим характером рельефа, при этом предельная погрешность изображения рельефа горизонталями не должна превышать 1/3 основного сечения.

Интерполяция (лат.) - вставка внутрь. При рисовке горизонталей на планах используют следующие способы интерполяции:

Интерполирование на глаз

При наличии достаточного опыта определение местоположения горизонталей производят на глаз, руководствуясь теми же положениями, которые приведены в аналитическом методе интерполяции. Построение горизонталей заключается в соединении плавными кривыми точек, найденных в результате интерполяции (аналитической, графической или на глаз). Начинать целесообразно с характерных по рельефу форм местности.

Аналитический, предусматривает определять расстояние до горизонталей из прямо пропорциональной зависимости между превышением и горизонтальным проложением между точками с подписанными на плане высотами.

Графическое интерполирование

Такое интерполирование, по сравнению с аналитическим, позволяет выполнить работу быстрее, с обеспечением необходимой точности. При графическом интерполировании используют интерполятор. Для построения интерполятора на кальке тушью вычерчивают ряд параллельных прямых линий на одинаковом расстоянии одна от другой (через 2, 4, 5 или 10 мм в зависимости от крутизны скатов данной местности и высоты сечения рельефа). Для определения местоположения горизонталей интерполятор накладывается так, чтобы число линий интерполятора между точками равнялось числу горизонталей на этом отрезке.

 Определение отметок точек местности по горизонталям

а) Точка лежит на горизонтали.
В этом случае отметка точки равна отметке горизонтали (см. рис. 35): H_А = 75 м; Н_С = 55 м.

б) Точка лежит на скате между горизонталями.
Если точка лежит между горизонталями, то через нее проводят кратчайшее заложение, масштабной линейкой измеряют длину отрезков а и b (см. рис. 35, точка В) и подставляют в выражение

где h – высота сечения рельефа. Если точка лежит между горизонталью и полугоризонталью, то вместо h в формулу подставляют 0,5h.

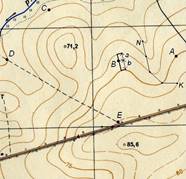
Рис. 35. Решение задач на карте с горизонталями

Определение крутизны ската

Крутизна ската по направлению заложения определяется двумя показателями – уклоном и углом наклона по формуле

Следовательно, тангенс угла наклона линии к горизонту называется её уклоном. Уклон выражают в тысячных – промиллях (‰) или в процентах (%). Например:  i = 0,020 = 20‰ = 2%.

Для графического определения углов наклона по заданному значению заложения d, масштабу М и высоте сечения рельефа h строят график заложений (см. рис. 36).

Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. От этих точек перпендикулярно к основанию графика откладывают в масштабе карты отрезки, равные соответствующим заложениям, а именно

Концы этих отрезков соединяют плавной кривой (см. рис. 36).

Заложение линии, угол наклона которой надо определить, снимают с карты при помощи измерителя, а затем, укладывая на графике между основанием и кривой измеренный отрезок, находят соответствующее ему значение угла наклона.

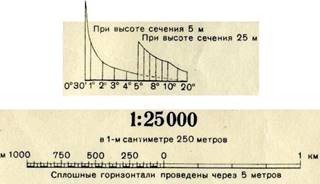
Рис. 36. График заложений для углов наклона

Аналогично строят и пользуются графиком заложений для уклонов (рис. 37).

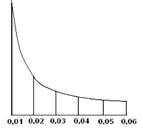
Рис. 37. График заложений для уклонов

Построение линии с заданным уклоном

Задача построения линии с заданным уклоном решается в проектировании трасс железных, автомобильных и других линейных сооружений. Она заключается в том, что из некоторой точки, обозначенной на карте, необходимо провести линию с заданным уклоном i по заданному направлению. Для этого сначала определяют значение заложения d, соответствующее заданным i и h. Его находят по графику заложения уклонов или вычисляют по формуле

  d = h/i .

Далее, установив раствор измерителя равным полученному значению d, ставят одну его ножку в начальную точку K, а другой засекают ближайшую горизонталь и тем намечают точку трассы, из которой в свою очередь засекают следующую горизонталь, и т.д. (см. рис. 38).

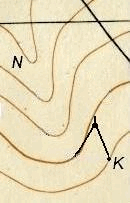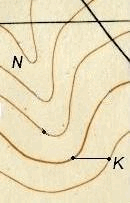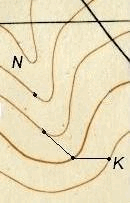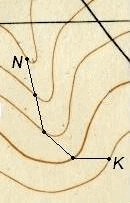
Рис. 38. Построение линии с заданным уклоном

Построение профиля по топографической карте

Профилем местности называют уменьшенное изображение вертикального разреза местности по заданному направлению.

Пусть требуется построить профиль местности по линии DE, указанной на карте (рис. 39). Для построения профиля на листе бумаги (как правило, используется миллиметровая бумага) проводят горизонтальную прямую и на ней, обычно в масштабе карты (плана), откладывают линию DE и точки её пересечения с горизонталями и полугоризонталями. Далее из этих точек по перпендикулярам откладывают отметки соответствующих горизонталей (на рис. 39 это отметки 50, 55, 60, 65, 70, 75, 80 и 82,5 м). Чтобы отобразить профиль более рельефно, отметки точек обычно откладывают в масштабе в 10 раз крупнее масштаба плана. Соединив прямыми концы перпендикуляров, получают профиль по линии DE.

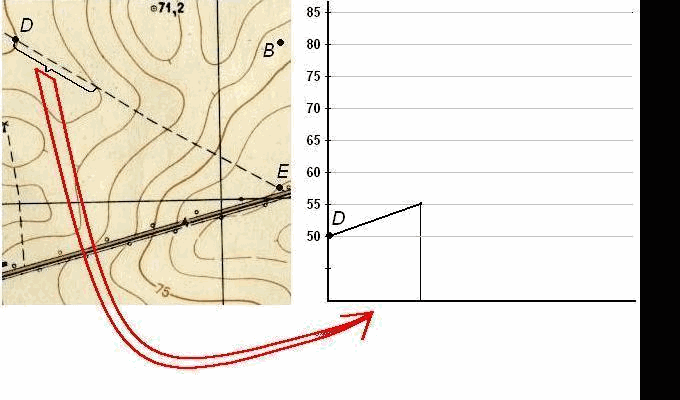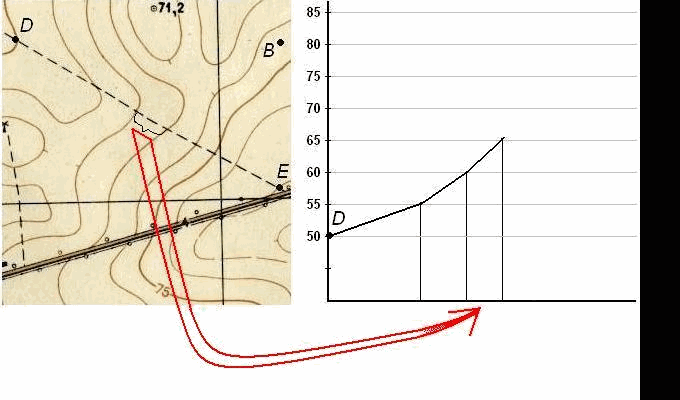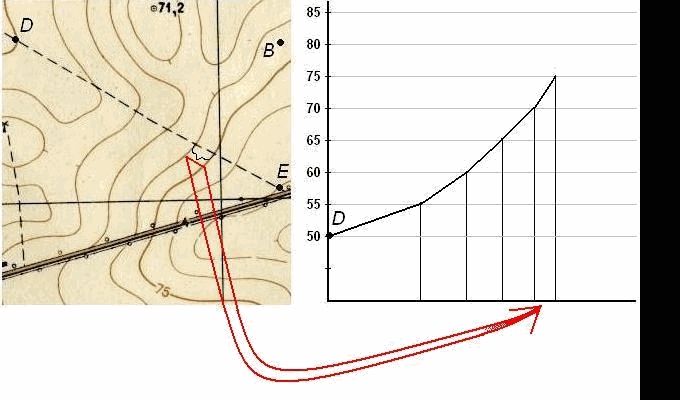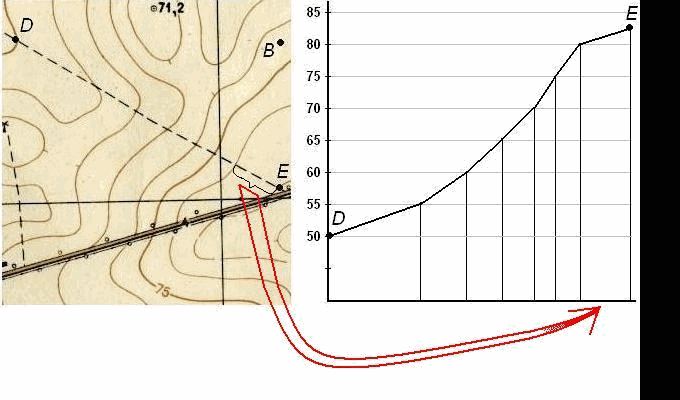
Рис. 38. Построение профиля по топографической карте

Лекция 12. Способы изображения рельефа местности на топографических картах и планах.

Изображение рельефа на планах и картах

Для решения инженерных задач изображение рельефа должно обеспечивать: во-первых, быстрое определение с требуемой точностью высот точек местности, направления крутизны скатов и уклонов линий; во-вторых, наглядное отображение действительного ландшафта местности.

Рельеф местности на планах и картах изображают различными способами (штриховкой, пунктиром, цветной пластикой), но чаще всего с помощью горизонталей (изогипсов), числовых отметок и условных знаков.

Горизонталь на местности можно представить как след, образованный пересечением уровенной поверхности с физической поверхностью Земли. Например, если представить холм, окружённый неподвижной водой, то береговая линия воды и есть горизонталь (рис. 30). Лежащие на ней точки имеют одинаковую высоту.

Допустим, что высота уровня воды относительно уровенной поверхности 110 м (рис. 30). Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Кривая линия пересечения поверхностей воды и холма будет соответствовать горизонтали с высотой 105 м. Если последовательно снижать уровень воды по 5 м и проектировать кривые линии, образованные пересечением поверхности воды с земной поверхностью, на горизонтальную плоскость в уменьшенном виде, то получим изображение рельефа местности горизонталями на плоскости.

Таким образом кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.

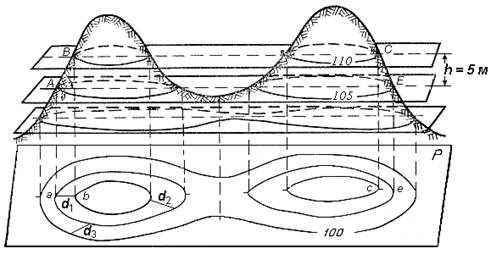
Рис. 30. Способ изображения рельефа горизонталями

При решении ряда инженерных задач необходимо знать свойства горизонталей:

1. Все точки местности, лежащие на горизонтали, имеют равные отметки.

2. Горизонтали не могут пересекаться на плане, поскольку они лежат на разных высотах. Исключения возможны в горных районах, когда горизонталями изображают нависший утес.

3. Горизонтали являются непрерывными линиями. Горизонтали, прерванные у рамки плана, замыкаются за пределами плана.

4. Расстояние между соседними горизонтальными секущими плоскостями h (см. рис. 30) называется высотой сечения рельефа. Оно равно разности высот двух соседних горизонталей.

Высота сечения рельефа в пределах плана или карты строго постоянна. Её выбор зависит от характера рельефа, масштаба и назначения карты или плана. Для определения высоты сечения рельефа иногда пользуются формулой

h = 0,2 мм · М,

где М – знаменатель масштаба.

Такая высота сечения рельефа называется нормальной.

5. Расстояние между соседними горизонталями на плане или карте называется заложением ската или склона. Заложение есть любое расстояние между соседними горизонталями (см. рис. 30), оно характеризует крутизну ската местности и обозначается d.

Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона ската ν (рис. 31). Чем больше угол наклона, тем круче скат.

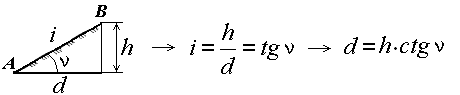
Рис. 31. Определение уклона и угла наклона ската

Другой характеристикой крутизны служит уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует (рис. 31), что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промиллях (‰).

Если угол наклона ската до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками. Например, обрыв показывается на планах и картах соответствующим условным знаком (рис. 32).

Изображение основных форм рельефа горизонталями приведено на рис. 32.

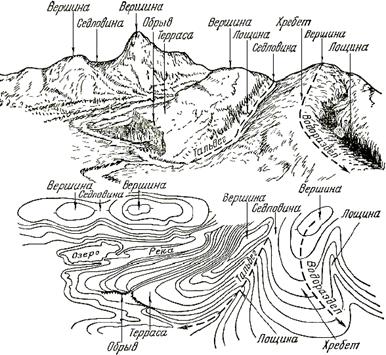
Рис. 32. Изображение форм рельефа горизонталями

Для изображения рельефа горизонталями выполняют топографическую съемку участка местности. По результатам съемки определяют координаты (две плановые и высоту) для характерных точек рельефа и наносят их на план (рис. 33). В зависимости от характера рельефа, масштаба и назначения плана выбирают высоту сечения рельефа h.

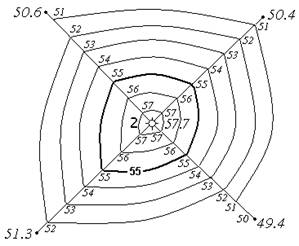
Рис. 33. Изображение рельефа горизонталями

Для инженерного проектирования обычно h = 1 м. Отметки горизонталей в этом случае будут кратны одному метру.

Положение горизонталей на плане или карте определяется с помощью интерполирования. На рис. 33 приведено построение горизонталей с отметками 51, 52, 53, 54, 55, 56, 57 м. Горизонтали кратные 5 или 10 м проводят на чертеже утолщенными и подписывают. Подписи наносят таким образом, чтобы верх цифр указывал сторону повышения рельефа. На рис. 33 подписана горизонталь с отметкой 55 м.

Там, где заложения больше, наносят штриховые линии (полугоризонтали). Иногда, чтобы сделать чертеж более наглядным, горизонтали сопровождают небольшими черточками, которые ставятся перпендикулярно горизонталям, по направлению ската (в сторону стока воды). Эти черточки называются бергштрихи.

Контрольные вопросы:

1. Что понимают под рельефом местности?

2. Назовите формы рельефа.

3. Что такое горизонталь? Назовите её основные свойства.

4. Что такое высота сечения рельефа?

5. Что называется заложением горизонталей?

6. Что такое уклон линии?

7. Как определяется нормальная высота сечения рельефа?

8. Как определить на карте высоту точки и крутизну ската линии?

Тема 1.4 Ориентирование линий.

Лекция 13. Страны света. Ориентирование линий на местности и на плане. Понятие азимута, дирекционного угла и румба.

Понятие об ориентировании

При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.

Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.

В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.

Азимут

Положение линии местности может быть определено относительно стран света с помощью одного из следующих горизонтальных углов: истинного или магнитного азимута, румба или дирекционного.

Истинным азимутом называется угол, составленный плоскостью истинного меридиана и плоскостью, проходящей через заданное направление. Угол отсчитывается от северной части меридиана по ходу часовой стрелки от 0 до 360°.

Магнитный азимут представляет собой угол между северным направлением меридиана и заданным направлением и отсчитывается от 0 до 360°. Направление магнитного меридиана определяется по магнитной стрелке, буссоли или компасу. Стрелка, будучи свободно подвешена и уравновешена, одним своим концом указывает на север, а другим — на юг. Магнитные меридианы сходятся в магнитных полюсах Земли, которые не совпадают с географическими полюсами. Поэтому магнитный азимут не равен истинному и отличается от него на некоторый угол, называемый склонением магнитной стрелки.

Склонение может быть восточным, если северный конец стрелки компаса или буссоли отклоняется к востоку от истинного меридиана, и западным — при отклонении стрелки к западу от него. Восточное склонение обозначают знаком «+» (плюс), а западное — знаком «—» (минус).

Величина склонения в одной и той же точке местности с течением времени непрерывно меняется. Различают вековое, годичное и суточное изменения склонения.         Возможны случаи, когда склонения магнитной стрелки в двух соседних пунктах значительно отличаются друг от друга. Такое явление называют магнитной аномалией. Примером может служить Курская магнитная аномалия.

Дирекционные углы и осевые румбы

Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 14).

Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.

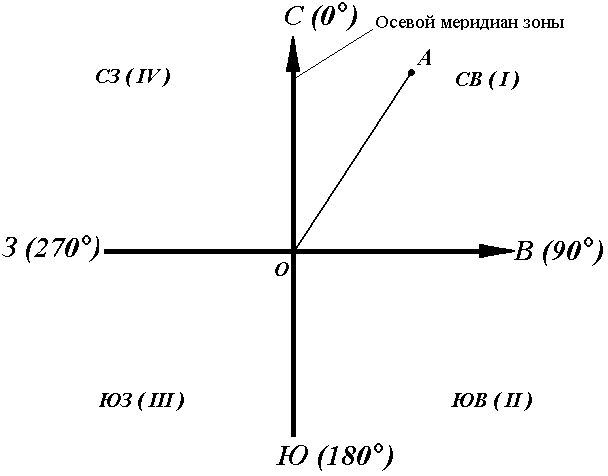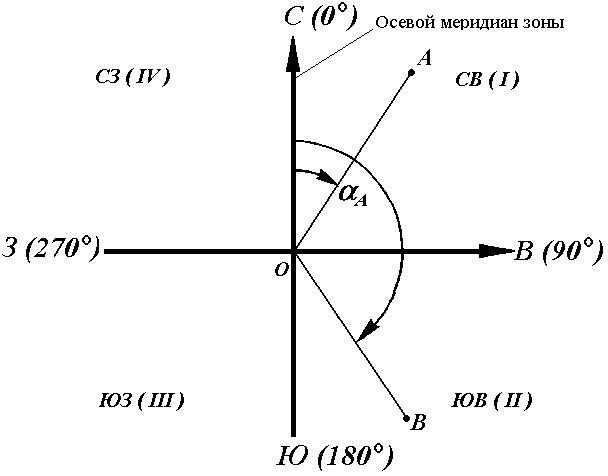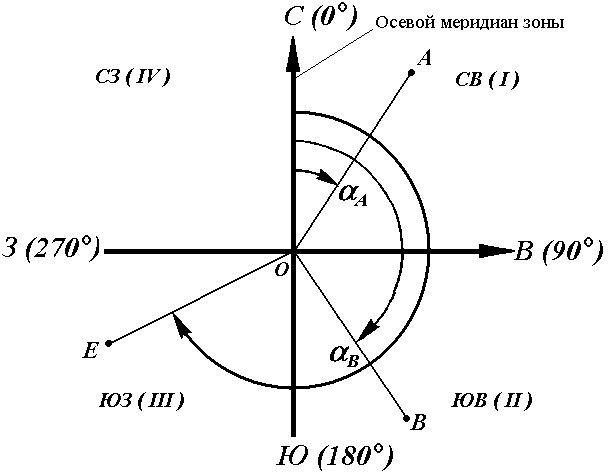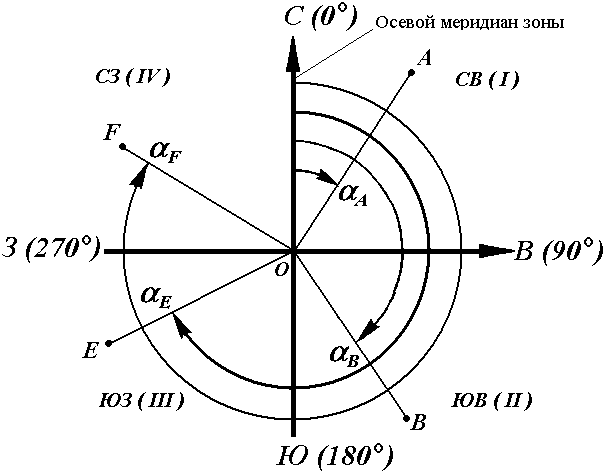
Рис. 14. Дирекционные углы

Для линии ОА её дирекционным углом в точке О является горизонтальный угол α_ОA  между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – α_ОВ , α_ОE , α_ОF.

Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.

В геодезии принято различать прямое и обратное направление линии (рис. 15). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим α_BC является прямым дирекционным углом линии ВС в точке М, а угол α_CB – обратным дирекционным углом этой же линии в той же точке.

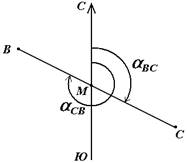
Рис. 15. Прямое и обратное направление линии

Из рисунка видно, что α_CB = α_BC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.

Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 16).

Осевым румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.

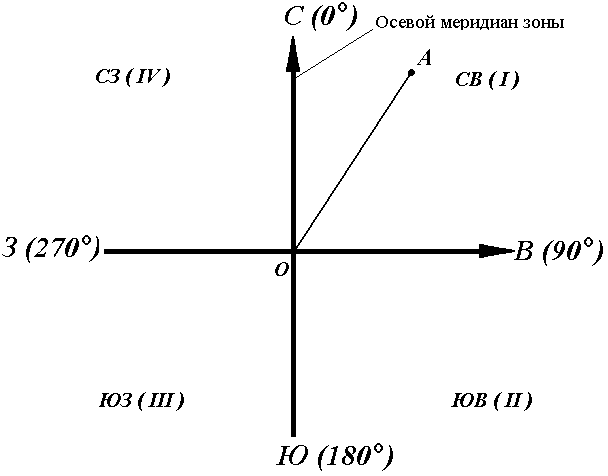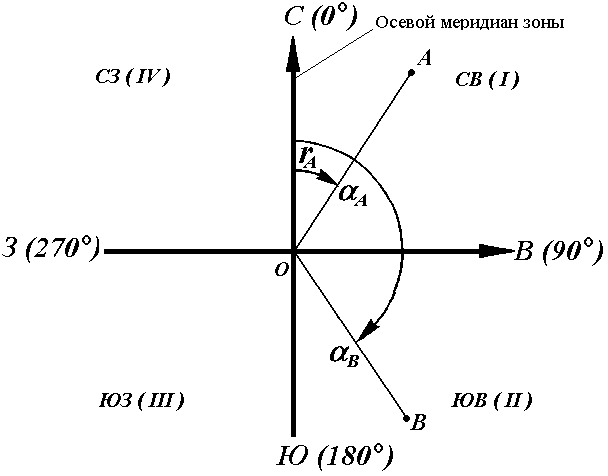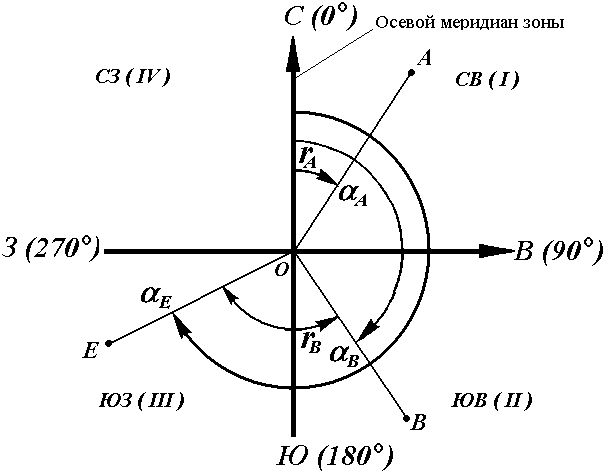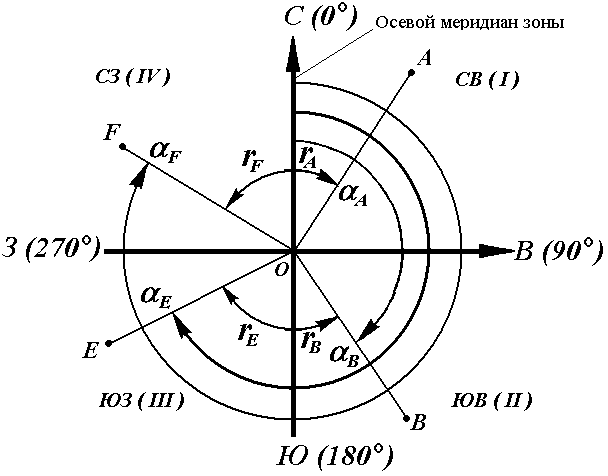
Рис. 16. Румбы и дирекционные углы

Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = α

II четверть (ЮВ) r = 180° – α

III четверть (ЮЗ) r = α – 180°

IV четверть (СЗ) r = 360° – α

Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.

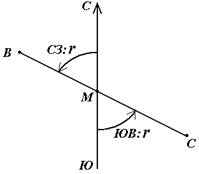
Рис. 17. Прямой и обратный румбы

Истинные азимуты и румбы

Кроме осевого меридиана зоны при ориентировании линий местности за основное направление может приниматься направление истинного (географического) меридиана.

Истинный меридиан – линия пересечения земной поверхности с плоскостью, проходящей через отвесную линию и ось вращения Земли.

Положение линии местности относительно истинного меридиана определяется истинным азимутом или истинным румбом.

Истинный азимут линии – угол в горизонтальной плоскости, отсчитываемый от северного направления истинного меридиана по ходу часовой стрелки до данной линии (рис. 18).

Истинный румб линии – острый горизонтальный угол, отсчитываемый от ближайшего направления истинного меридиана (северного или южного) до данной линии.

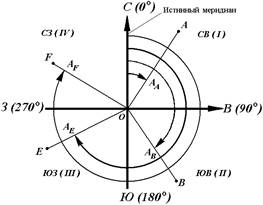
Рис. 18. Истинные азимуты

Истинный азимут A измеряется от 0° до 360°. Зависимость между истинными азимутами и румбами такая же, как и между дирекционными углами и осевыми румбами.

Истинные меридианы, проходящие через точки Земли с разной долготой, не параллельны между собой и сходятся на полюсах. Поэтому азимуты одной и той же прямой линии, определяемые относительно разных истинных меридианов, отличаются на величину γ (рис. 19), которую называют углом сближения меридианов. Его приближенное значение можно рассчитать по формулам:

 γ = 0,54 · l · tgφ   или  γ = sinφ · Δλ,

где l – длина прямой линии между точками (км); φ – средняя широта линии; Δλ – разность долгот. При l = 1 км и широте Хабаровска φ = 48°28' угол сближения меридианов γ = 0,6' = 36".

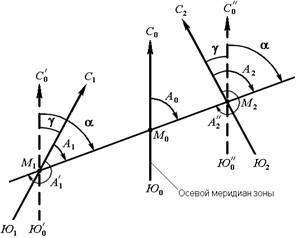
Рис. 19. Зависимость между истинным азимутом и дирекционным углом

Для перехода от дирекционного угла к истинному азимуту и наоборот необходимо знать угол сближения γ между осевым и истинным меридианом (рис. 19). Зависимость между истинным азимутом и дирекционным углом следующая

А = α + γ .

Если точка расположена к западу от осевого меридиана, то величину угла сближения γ между осевым и истинным меридианом принято считать отрицательной, если к востоку – положительной (рис. 21). Например, истинные азимуты линии при дирекционном угле α = 70° и углах сближения γ =  – 0°50' для западной точки М1, γ = 0°50' для восточной – М2 соответственно равны

А₁ = 70° – 0°50' = 69°50',

А₂ = 70° + 0°50' = 70°50'.

2.2.3. Магнитные азимуты и румбы

При ориентировании линий местности за основное направление может также приниматься направление магнитного меридиана.

Магнитная стрелка на концах имеет точки, в которых сосредоточены магнитные массы. Соединяющая их линия называется магнитной осью стрелки.

Вертикальная плоскость, проходящая через магнитную ось стрелки, является плоскостью магнитного меридиана.

Линия пересечения плоскости магнитного меридиана с горизонтальной плоскостью дает направление магнитного меридиана.

Горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки до данной линии, называется магнитным азимутом А_м (рис. 20).

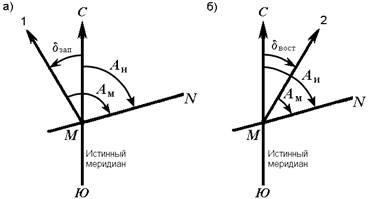
Рис. 20. Магнитный азимут и склонение магнитной стрелки: а) западное; б) восточное

В каждой точке на поверхности Земли магнитный и истинный меридианы образуют между собой угол, называемый склонением магнитной стрелки δ (рис. 22). Северный конец магнитной стрелки может отклоняться от истинного меридиана к западу или востоку. В зависимости от этого различают западное и восточное склонения. Восточное склонение принято считать положительным, западное – отрицательным:

А_и = А_м + δ_вост ,

А_и = А_м – δ_зап .

Магнитное склонение в разных пунктах Земли различно и непостоянно. Различают вековые, годовые и суточные изменения склонения. В связи с этим магнитная стрелка указывает направление магнитного меридиана приблизительно и ориентировать линию по нему можно только тогда, когда не требуется большая точность ориентирования.

Связь между дирекционными углами предыдущей и последующей линий

На рис. 21 представлена схема определения дирекционных углов сторон теодолитного хода AB. Известен дирекционный угол исходной стороны α₀ и измерены геодезическим прибором теодолитом углы β₁, β₂, β₃, лежащие справа по ходу от А к В.

Рис. 21. Схема определения дирекционных углов сторон теодолитного хода

Лекция 14. Ориентирующие углы, длины линий местности и связь между ними.

Определение горизонтальных углов между направлениями

Пусть имеются две линии BC и CD; угол между ними в точке C равен β_ПР (правый по ходу BCD угол) – рис.  Проведем через точки B и C направления, параллельные осевому меридиану зоны и покажем на рисунке дирекционные углы α_ВС и α_СD. В задаче известны α_ВС и β_пр; требуется найти α_СD.

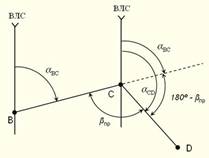
Рис.  Правый по ходу угол β_пр

Продолжим линию BC (пунктирная) и покажем на ее продолжении угол α_ВС. Из рис.  видно, что α_СD = α_ВС + (180º – β_пр)

Если измерен  левый по ходу ВСD угол β_лев , то формула примет вид

α_СD = α_ВС + (β_лев – 180º)

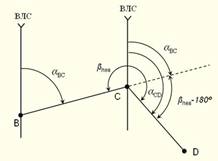
Рис. Измерен левый по ходу угол β_лев

Если при вычислении по двум последним формулам дирекционный угол примет отрицательные значения, к нему прибавляют 360º; если он будет больше 360º, то из него вычитают 360º.

Связь между дирекционными углами предыдущей и последующей линий

На рис. 21 представлена схема определения дирекционных углов сторон теодолитного хода AB. Известен дирекционный угол исходной стороны α₀ и измерены геодезическим прибором теодолитом углы β₁, β₂, β₃, лежащие справа по ходу от А к В.

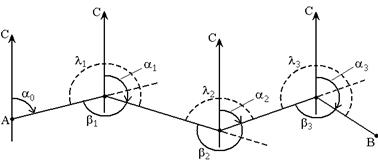
Рис. 21. Схема определения дирекционных углов сторон теодолитного хода

Найдём дирекционные углы α₁, α₂, α₃ остальных сторон хода.

На основании зависимости между прямыми и обратными дирекционными углами можем написать:

α₁ + β₁ = α₀ + 180° из данного выражения следует, что α₁ = α₀ + 180° – β₁ (1).

Аналогично вычисляются дирекционные углы последующих сторон теодолитного хода:

α₂ + β₂ = α₁ + 180°  →  α₂ = α₁ + 180° – β₂ (2)

α₃ + β₃ = α₂ + 180°  →  α₃ = α₂ + 180° – β₃ (3)

...............................................................................

α_n + β_n = α_n-1 + 180°  →  α_n = α_n-1 + 180° – β_n (n)

То есть, дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус угол, лежащий справа по ходу.

Для получения контрольной формулы в выражение (2) подставим значение α₁, из выражения (1)

α₂ = α₀ + 2 ∙ 180° – (β₁ + β₂) .

Если продолжить аналогичные действия для последующих сторон теодолитного хода, то  получим

α_n = α₀ + n ∙ 180° – (β₁ + β₂ + β₃ + ... + β_n) .

или

α_n – α₀ = n ∙ 180° – ∑β .

или

α₀ – α_n = ∑β – n ∙ 180° .

Эта формула может служить контрольной при вычислении дирекционных углов по увязанным углам β.

Если же вместо суммы исправленных углов подставить сумму измеренных углов ∑β, то та же формула позволит определить невязку f_β измеренных углов теодолитного хода, если дирекционные углы α₀ и α_n начальной и конечной сторон хода известны

f_β = ∑β – n ∙ 180° – (α₀ – α_n).

Иногда дирекционные углы вычисляют по углам, лежащим слева по ходу от А до В (λ₁, λ₂, …, λ_n).

β₁ = 360° – λ₁

β₂ = 360° – λ₂

........................

β_n = 360° – λ_n

Подставим эти значения в выражения (1), (2), ..., (n)  получим

α₁ = α₀ – 180° + λ₁

α₂ = α₁ – 180° + λ₂

.................................

α_n = α_n-1 – 180° + λ_n .

Для проверки правильности вычисления дирекционных углов по углам λ, лежащим слева по ходу, используют выражения

α_n – α₀ = ∑λ  – n ∙ 180°

 или

α_n – α₀ = ∑λ  + n ∙ 180°.

Тогда невязка f_β определяется по формуле

f_β = ∑λ + n ∙ 180° – (α_n – α₀).

Связь между дирекционным углом и азимутом

В пределах каждой шестиградусной или трехградусной зоны для ориентирования линий пользуются не истинным меридианом, а линией, параллельной осевому меридиану. Тогда вместо азимутов применяют дирекционные углы. Как и азимут, дирекционный угол измеряется по ходу часовой стрелки от положительно направления оси абсцисс до ориентируемой линии. Величина дирекционного угла изменяется от 0 до 360°.

Если через точку Р линии PQ  проходит истинный меридиан СЮ и линия NS параллельна осевому меридиану, то угол будет углом сближения меридианов, а угол — дирекционным углом линии PQ.

Для линии PQ дирекционный угол будет прямым, для линии QP угол будет обратным дирекционным углом.

Прямой и обратный дирекционные углы всегда различаются между собой на 180°. Дирекционный угол одной и той же линии в отличие от азимута в разных ее точках остается постоянным.

Для удобства вычислений часто вместо дирекционных углов пользуются румбами. Зависимость между дирекционными углами и румбами в разных четвертях аналогична зависимости между азимутами и румбами и выражается формулами:

I (СВ) а=г;     г=а;

ЩЮВ) а=180° - г;     г=180° - а;

III (ЮЗ) а=180° + г;  г=а - 180°

IV(C3) а=360° + г;    г=360°- а

Связь между дирекционными углами и румбами

Лекция 15. Определение обратных дирекционных углов и румбов.

В геодезии принято различать прямое и обратное направление линии. Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим α_BC является прямым дирекционным углом линии ВС в точке М, а угол α_CB – обратным дирекционным углом этой же линии в той же точке.

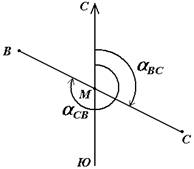
Рис. Прямое и обратное направление линии

Из рисунка видно, что α_CB = α_BC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.

Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами.

Осевым румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.

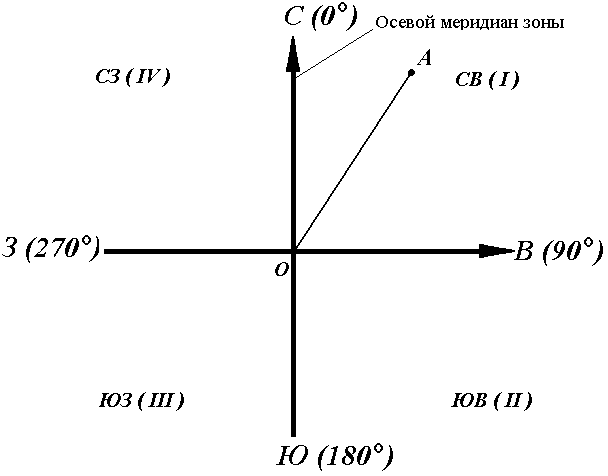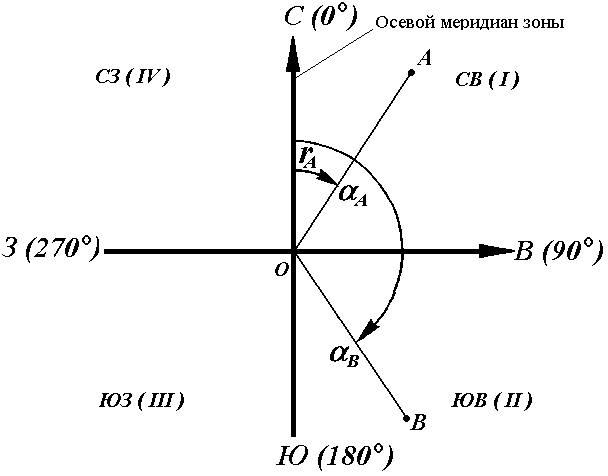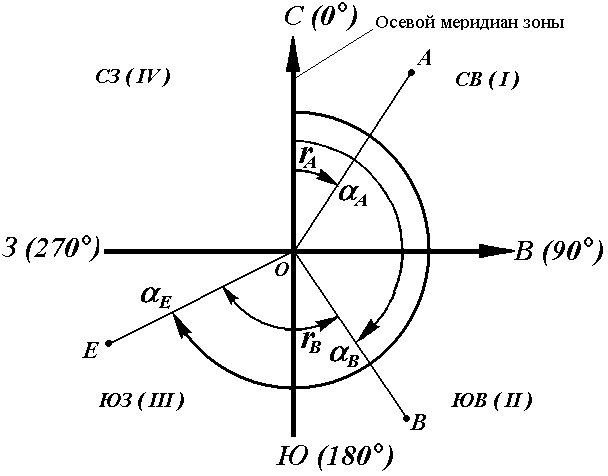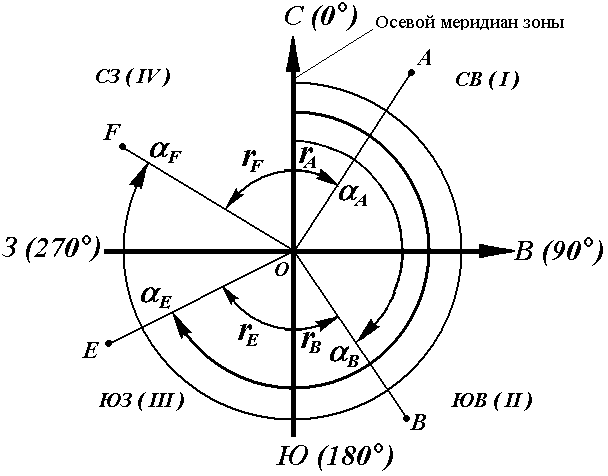
Рис. Румбы и дирекционные углы

Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = α

II четверть (ЮВ) r = 180° – α

III четверть (ЮЗ) r = α – 180°

IV четверть (СЗ) r = 360° – α

Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.

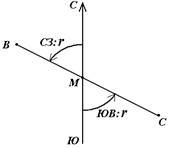
Рис. Прямой и обратный румбы

Обратный азимут характеризуется углом, образованным направлением истинного меридиана и обратным направлением данной линии.

В ряде случаев для удобства вычислений направление выражают не в азимутах, а в румбах.

Лекция 16. Простейшие способы съемки. Составление плана местности.

Горизонтальной съемкой называется совокупность измерительных действий на местности, дающих возможность построить графическое изображение горизонтальной проекции этой местности.
 Способ разбивки участка на треугольники.  При разбивке участка на треугольники  в каждом из них строят экером высоту и измеряют лентой основание и высоту. Результаты измерений тут же заносят на схематический чертеж, называемый абрисом (Нем. Abris – чертеж). В дальнейшем по этим данным строят в заданном масштабе треугольники на бумаге, получая план снятого участка. Способ разбивки на треугольники применим на открытой местности.

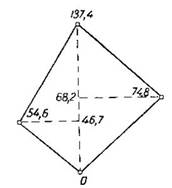
Рис. Абрис съемки разбивкой участка местности на треугольники.

Способ прямоугольных координат

Для съемки прокладывают прямую линию – магистраль (AВ на рис.). От точки А начинают измерение длины этой линии. Из контурных точек (на рисунке – из точек поворота ограды и углов дома) на магистраль AB с помощью экера опускают перпендикуляры, лентой измеряют длины этих перпендикуляров и измеряют расстояния от начальной точки A до основания каждого перпендикуляра. При съемке отмечаются также точки пересечения ограды с магистралью АВ и точки пересечения линий, являющихся продолжением стен дома, с линией AB.
При съемке ведется абрис – глазомерно составляемый чертеж, на котором показывают все снимаемые объекты и записывают числовые результаты всех измерений. По записям в абрисах впоследствии составляют план снятого участка.
Для контроля положения граничных пунктов участка измеряют лентой длины линий между соседними пунктами. При этом отмечают расстояния от начала данной линии до точек пересечения ее с контурами местности (например, с краями дороги, берегами речки и т. п.). Такой способ съемки называется способом промеров с точки на точку.

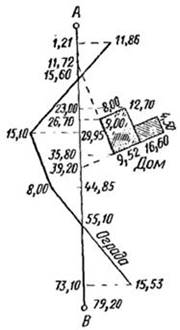
Рис. Абрис съемки способом прямоугольных координат (перпендикуляров).

При составлении плана участка, снятого способом прямоугольных координат, сначала наносят в заданном масштабе на бумагу магистраль. Затем откладывают на ней измеренные абсциссы. В полученных точках строят перпендикуляры и откладывают измеренные ординаты граничных пунктов участка. Для контроля сравнивают полученные на плане и измеренные на местности расстояния между соседними пунктами. Убедившись в правильности их нанесения, накладывают снятую ситуацию, после чего оформляют план в установленных условных знаках.

Способ обхода

Для съемки таких объектов, в середине которых невозможно проложить магистраль (например, труднопроходимое болото, озеро, пруд), вблизи их границ разбивают многоугольник с прямыми углами. Углы этого многоугольника строят экером, а стороны измеряют лентой. Изгибы границы снимают способом прямоугольных координат относительно ближайшей стороны многоугольника.

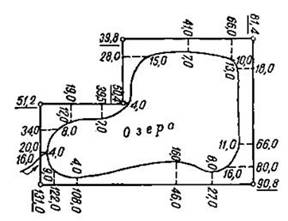
Рис. Абрис съемки способом обхода и прямоугольных координат.

Построение плана участка, снятого способом обхода, начинают с нанесения многоугольника. Затем на его основе наносят всю снятую ситуацию.
Недостаток плана, составленного по результатам съемки экером и лентой, состоит в отсутствии ориентировки относительно сторон горизонта.

Контрольные вопросы:

1. Что называется ориентированием на местности?

2. Что называется дирекционным углом линии, и в каких пределах он измеряется?

3. Что такое румб линии, и в каких пределах он измеряется?

4. Что называется истинным и магнитным азимутами?

5. Какова зависимость между дирекционным углом и истинным азимутом и между истинным азимутом и магнитным азимутом?

6. Что называется сближением меридианов?

7. Что называется склонением магнитной стрелки?

Тема 1.5 Линейные измерения.

Лекция 17. Мерные приборы и методика измерения линий местности.

Приборы, используемые для линейных измерений, условно делят на три группы: механические, оптические и физико-оптические. Механические приборы используются для непосредственного измерения расстояний. К ним относятся землемерные ленты, рулетки, тросы, длинномеры, инварные проволоки и др. Из оптических дальномеров наибольшее распространение получили нитяный дальномер и дальномеры с переменной базой и переменным параллактическим углом. К физико-оптическим приборам относят электромагнитные дальномеры и светодальномеры.
На лесных съемках для непосредственного измерения расстояний используют землемерные ленты и рулетки, для дистанционного – дальномеры.
Для измерения коротких расстояний применяют рулетки тесьмовые и стальные. Тесьмовая рулетка может иметь длину 3; 10 и 20 м. На ее ленте нанесены деления через 1 см, а подписаны каждые 10 см и целые метры.
Рулетки измерительные металлические выпускают нескольких типов: РС – самосвертывающаяся; РЖ – желобчатая; РЗ – в закрытом корпусе; РК – на крестовине; РВ – на вилке; РЛ – с грузом. У рулеток типа А начало шкалы сдвинуто от торца ленты, а у рулеток типа В начало шкалы совпадает с торцом ленты.

Землемерные ленты изготавливают длиной 20 м, 24 м и 50 м. Обозначают землемерные ленты буквами ЛЗ (лента землемерная) и ЛЗШ (лента землемерная штриховая). Изготавливают их из стальной полосы, которая наматывается на барабан. На обоих концах ленты имеются рукоятки, предназначенные для выравнивания полосы на поверхности земли и обеспечения необходимого натяжения при измерениях силой 10 кг. Лента землемерная разделена на метры и дециметры. Метры обозначены ромбическими пластинами с порядковыми номерами метров. Необходимо помнить, что на разных сторонах полотна ленты надписи возрастают в противоположных направлениях. Лента хранится в свернутом положении на специальном кольце. Сворачивая или снимая ленту с кольца, необходимо избегать образования петель.
В комплект ленты входят 11 или 6 шпилек

Ленту перед измерениями компарируют, т. е. сравнивают ее с эталонной (нормальной) мерой. Выполняют сравнение на полевом компараторе.

Длинномер относят к подвесным мерным приборам. В длинномере стальную проволоку натягивают между двумя фиксированными на местности точками. По проволоке в процессе измерения прокатывают устройство, основными элементами которого являются мерный диск и счетный механизм, позволяющий установить количество оборотов диска на прокатываемом отрезке проволоки

Инварная проволока (сплав железа с никелем, обладает малым температурным коэффициентом линейного расширения), как и длинномер, представляет собой подвесной мерный прибор. В процессе измерения, ее основная часть – 24-метровая проволока, последовательно натягивается между соседними штативами, равномерно расставленными вдоль линии. Измерение длин линий инварными проволоками отличается высокой точностью, но требует больших затрат труда и времени.

Жезлы представляют собой профилированные металлические линейки с делениями 0,1 мм и встроенным в корпус линейки термометром. В длину жезла вводят поправку за температуру, если она будет отличаться от температуры, при которой определялась длина жезла при компарировании. Номинальная длина жезлов стандартная – 2 и 3 м. Жезлы используют для компарирования рулеток, их шкал, а также шкал и интервалов нивелирных реек различной точности и назначения, для точных разбивок базисов на местности.

Оптическим дальномером называют прибор, в котором для определения расстояний используются оптические элементы. Из оптических дальномеров наибольшее распространение получили нитяный дальномер и дальномеры с переменной базой и переменным параллактическим углом.

Нитяный дальномер имеется практически во всех геодезических приборах (теодолитах, нивелирах). Сетка нитей зрительной трубы содержит две дальномерные нити, проекция которых через зрительную трубу в пространство предмета образует параллактический угол
При определении расстояний нитяным дальномером используют рейки МN с сантиметровыми делениями.

Лекция 18. Вешение линий. Оценка точности измерения линий.

Вешение линий. Оценка точности измерения линий.

Перед измерением линию закрепляют, провешивают и расчищают. Закрепление состоит в установке на концах линии временных или постоянных знаков и вех. Длинную прямую обозначают промежуточными вехами. Обозначение линии на местности рядом отвесно поставленных вешек, находящихся в одной вертикальной плоскости называют вешение линии. Оно необходимо для того, чтобы в процессе измерения можно было укладывать ленту с возможно малыми отклонениями от створа – вертикальной плоскости, проходящей через концы линии.
Используют вехи фабричного производства или изготовленные из подручных материалов; длина их 1,5 – 2,5 м, толщина 4 – 6 см.

Измерение ведут два мерщика – передний и задний. Второй (задний) берет себе одну шпильку, а первый – все остальные (10 или 5) и, разматывая ленту, идет по линии. Задний ставит шпильку в начальную точку, зацепляет за нее конец ленты и показывает переднему, как уложить ленту в створ. Находясь в створе линии, передний мерщик встряхивает ленту, укладывает ее на землю и вставляет шпильку в переднюю прорезь ленты. Выполнив первую укладку ленты, задний мерщик вынимает из земли шпильку, а передний аккуратно выводит ленту из зацепления со шпилькой и оставляет последнюю в земле. Взяв ленту за ручки, мерщики идут вперед по заданной линии и останавливаются тогда, когда задний мерщик подходит к шпильке, оставленной в земле передним. Описанным выше способом откладывают вторую ленту. В дальнейшем мерщики повторяют свои действия до тех пор, пока передний не израсходует все шпильки; задний передает ему собранные шпильки, кроме одной, находящейся в земле, и они продолжают измерение. Число передач шпилек отмечают оба мерщика. Подойдя к конечной точке, они отсчитывают остаток с точностью до 0,01 м (расстояние между последней шпилькой и концом линии) и подсчитывают длину линии.
Линию обязательно измеряют в обратном направлении и из двух результатов, если они сходятся в пределах допуска, вычисляют среднюю длину Dcp и добавляют к ней поправку за компарирование ленты.

         Лекция 19. Определение недоступных расстояний.

Определение недоступных расстояний

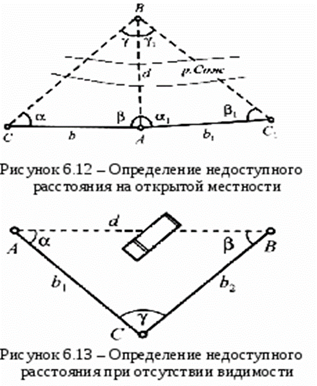
В практике геодезических работ часто оказывается невозможным непосредственное измерение расстояний между двумя точками, когда встречается местное препятствие (река, котлован, здание и т. д.). Такие расстояние называют недоступными и определяют косвенным путем. Например, для определения недоступного расстояния d через реку измеряют длину базиса b  и углы α и β. По теореме синусов из треугольника АВС получим d / sin α = b / sin γ = b / sin(180⁰ – α – β) = b / sin α + β) или d = b sin α / sin(α + β). Для контроля расстояниеd определяют еще раз из треугольника АВС₁. При отсутствии недопустимых расхождений из двух результатов принимают среднее арифметическое значение.

Точность определения недоступных расстояний во многом зависит от формы треугольника. Наилучшим считается равносторонний треугольник.

В том случае, когда на линии АВ нет видимости , то для определения недоступного расстояния АВ измеряют длины сторон b₁ и b₂ и угол γ на точке С.

Расстояние d определяют по теореме косинусов:

___________________

d =√ b₁² + b₂² – 2b₁b₂ cos γ.

Наиболее благоприятным считается вариант, когда b₁ =b₂ и угол γ близок к 180^о

sin α = b₂ sin γ / d; sin β = b₁ sin γ / d.

Углы α и β вычисляют для того, чтобы в точках А и В можно было указать направление линии d.

Контрольные вопросы:

1. Что называется вешением линии?

2. Что такое створ линии?

3. Какие приборы применяются для непосредственного измерения расстояний?

4. Что такое компарирование мерных приборов?

5. Как измеряются линии стальной мерной штриховой лентой?

6. Как приводятся наклонные расстояния к горизонту?

7. От чего зависит точность измерения линии мерной лентой?

Тема 1.6 Угловые измерения.

Лекция 20. Геодезические измерения углов. Единицы и технические средства измерения углов.

Угловые геодезические измерения – вид геодезических измерений, в которых измеряемой геодезической величиной являются горизонтальные и (или) вертикальные углы (зенитные расстояния). Измерение горизонтальных и вертикальных углов на местности выполняют специальными приборами – теодолитами.

Горизонтальный угол – это ортогональная проекция пространственного угла на горизонтальную плоскость. Обозначается буквой β.

Вертикальный угол – это плоский угол, лежащий в вертикальной плоскости. К вертикальным углам относятся угол наклона и зенитное расстояние.

Угол между горизонтальной плоскостью и направлением линии местности называется углом наклона и обозначается буквой ν . Углы наклона бывают положительные и отрицательные.
Угол между вертикальным направлением и направлением линии местности называется зенитным расстоянием и обозначается буквой z. Зенитные расстояния всегда положительные.
Угол наклона и зенитное расстояние одного направления связаны соотношением:
ν = 90 – z   или   z = 90 – ν.

Углы обычно измеряют в градусной мере (градусы, минуты, секунды), реже - в радианной. За рубежом широко применяется градовая мера измерения углов.

При геодезических работах измеряют не углы между сторонами на местности, а их ортогональные (горизонтальные) проекции, называемые горизонтальными углами. Так, для измерения угла АВС, стороны которого не лежат в одной плоскости, нужно предварительно спроектировать на горизонтальную плоскость точки А, В, и С (рис. 40) и измерить горизонтальный угол abc = β (рис.39).

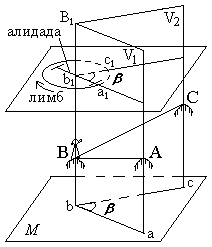
Рис. 40. Принцип измерения горизонтального угла

Рассмотрим двугранный угол между вертикальными плоскостями V₁ и V₂ , проходящими через стороны угла АВС. Угол β для данного двугранного угла является линейным. Следовательно, углу β равен всякий другой линейный угол, вершина которого находится в любой точке на отвесном ребре ВВ₁ двугранного угла, а стороны его лежат в плоскости, параллельной плоскости М. Итак, для измерения величины угла abc = β можно в любой точке, лежащей на ребре ВВ₁ двугранного угла, допустим в точке b₁, установить горизонтальный круг с градусными делениями и измерить на нем дугу a₁c₁, заключенную между сторонами двугранного угла, которая и будет градусной мерой угла a₁b₁c₁, равной β , т.е. угол abc = β.

Лекция 21. Основные геодезические приборы, их устройство, поверки и порядок юстировки. Назначение теодолита.

Теодолит, его составные части  

Измерения горизонтальных проекций углов между линиями местности производят геодезическим угломерным прибором теодолитом. Для этого теодолит имеет горизонтальный угломерный круг с градусными делениями, называемый лимбом. Стороны угла проектируют на лимб с использованием подвижной визирной плоскости зрительной трубы. Она образуется визирной осью трубы при её вращении вокруг горизонтальной оси. Данную плоскость поочередно совмещают со сторонами угла ВА и ВС, последовательно направляя визирную ось зрительной трубы на точки А и С. При помощи специального отсчетного приспособления алидады, которая находится над лимбом соосно с ним и перемещается вместе с визирной плоскостью, на лимбе фиксируют начало и конец дуги a₁c₁ (см. рис. 40), беря отсчеты по градусным делениям. Разность взятых отсчетов является значением измеряемого угла β.

Лимб и алидада, используемые для измерения горизонтальных углов, составляют в теодолите горизонтальный круг. Ось вращения алидады горизонтального круга называют основной осью теодолита.

В теодолите также имеется вертикальный круг с лимбом и алидадой, служащий для измерения вертикальных проекций углов – углов наклона. Принято считать углы наклона выше горизонта положительными, а ниже горизонта – отрицательными. Лимб вертикального круга обычно наглухо скреплён со зрительной трубой и вращается вместе с ней вокруг горизонтальной оси теодолита.

Перед измерением углов центр лимба с помощью отвеса или оптического центрира устанавливают на отвесной линии, проходящей через вершину измеряемого угла, а плоскость лимба приводят в горизонтальное положение, используя с этой целью три подъемных винта 3 и цилиндрический уровень 12 (рис. 41). В результате данных действий основная ось теодолита должна совпасть с отвесной линией, проходящей через вершину измеряемого угла.

Рис. 41. Устройство теодолита 4Т30П:
1 – головка штатива; 2 – основание; 3 – подъемный винт; 4 – наводящий винт алидады; 5 – закрепительный винт алидады; 6 – наводящий винт зрительной трубы; 7 – окуляр зрительной трубы; 8 – предохранительный колпачок сетки нитей зрительной трубы; 9 – кремальера; 10 – закрепительный винт зрительной трубы; 11 – объектив зрительной трубы; 12 – цилиндрический уровень; 13 – кнопочный винт для поворота лимба; 14 – закрепительный винт; 15 – окуляр отсчетного микроскопа с диоптрийным кольцом; 16 – зеркальце для подсветки штрихов отсчетного микроскопа; 17– колонка; 18 – ориентир-буссоль; 19 – вертикальный круг; 20 – визир; 21 – диоптрийное кольцо окуляра зрительной трубы; 22 – исправительные винты цилиндрического уровня; 23 – подставка.

Для установки, настройки и наведения теодолита на цели в нем имеется система винтов: становой и подъемные винты, закрепительные (зажимные) и наводящие (микрометренные) винты, исправительные (юстировочные) винты.

Становым винтом теодолит крепят к головке штатива, подъемными винтами – горизонтируют.

Закрепительными винтами скрепляют подвижные части теодолита (лимб, алидаду, зрительную трубу) с неподвижными. Наводящими винтами сообщают малое и плавное вращение закрепленным частям.

Чтобы теодолит обеспечивал получение неискаженных результатов измерений, он должен удовлетворять соответствующим геометрическим и оптико-механическим условиям. Действия, связанные с проверкой этих условий, называют поверками. Если какое-либо условие не соблюдается, с помощью исправительных винтов производят юстировку прибора.

Выполнение основных поверок теодолита и их юстировка

Поверки теодолита выполняют для контроля соблюдения в приборе верного взаиморасположения его осей. Основными поверками являются следующие.
Поверка уровня. Ось цилиндрического уровня на алидаде горизонтального круга должна быть перпендикулярна к оси вращения алидады.
Перед выполнением поверки выполняют горизонтирование теодолита. Затем устанавливают уровень по направлению двух подъёмных винтов и с их помощью приводят пузырёк в нуль-пункт. Поворачивают алидаду на 180º. Если пузырёк уровня остался в нуль-пункте, то требуемое условие выполнено – ось уровня перпендикулярна к оси вращения алидады. Если пузырёк уровня ушел из нуль-пункта, исправительными винтами уровня изменяют его наклон, перемещая пузырёк в сторону нуль-пункта на половину отклонения. Поверку повторяют, добиваясь, чтобы смещение пузырька было меньше одного деления.
Поверка сетки нитей. Вертикальный штрих сетки нитей должен быть перпендикулярен к оси вращения зрительной трубы.
Наводят вертикальный штрих сетки нитей на точку и наводящим винтом трубы изменяют ее наклон. Если изображение точки не скользит по штриху, сетку нитей надо повернуть. Для этого поворачивают корпус окуляра, ослабив четыре винта его крепления к зрительной трубе.

Поверка визирной оси. Визирная ось трубы должна быть перпендикулярна к оси вращения трубы. Если визирная ось перпендикулярна к оси вращения трубы, то отсчёты по горизонтальному кругу при разных положениях вертикального круга (КЛ и КП) и наведении на одну и ту же точку будут различаться ровно на 180º. Если разность отчетов отличается от 180°, то ось вращения трубы не перпендикулярна к визирной оси. При этом соответствующие отсчёты КЛ и КП отличаются от правильных значений на одинаковую величину с, получившую название коллимационной ошибки.
При выполнении поверки визируют на удалённую точку при двух положениях круга и берут отсчёты КЛ и КП. Вычисляют коллимационную погрешность
с = (КЛ - КП ± 180°) ¤ 2, которая не должна превышать двойной точности теодолита. 

Если коллимационная погрешность велика, то наводящим винтом алидады устанавливают на горизонтальном круге верный отсчёт, равный (КЛ - с) или (КП + с). При этом центр сетки нитей сместится с изображения точки. Отвинчивают колпачок, закрывающий винты сетки нитей, ослабляют один из вертикальных исправительных винтов, и, действуя горизонтальными исправительными винтами, совмещают центр сетки нитей с изображением точки. Закрепив ослабленные винты, поверку повторяют.

Поверка оси вращения трубы. Ось вращения трубы должна быть перпендикулярна к оси вращения алидады.
Установив теодолит вблизи стены здания, визируют на высоко расположенную под углом наклона 25 - 30º точку. Наклоняют трубу до горизонтального положения и отмечают на стене проекцию центра сетки нитей. Переводят трубу через зенит, вновь визируют на точку  и отмечают её проекцию. Если изображения обеих проекций точки не выходят за пределы биссектора сетки нитей, требование считают выполненным. В противном случае необходимо исправить положение оси вращения трубы. Исправление выполняют в мастерской, изменяя наклон оси.

Классификация теодолитов

В настоящее время отечественными заводами в соответствии с действующим ГОСТ 10529 – 96 изготавливаются теодолиты четырех типов: Т05, Т1, Т2, Т5 и Т30.

Для обозначения модели теодолита используется буква "Т" и цифры, указывающие угловые секунды средней квадратической ошибки однократного измерения горизонтального угла.

По точности теодолиты подразделяются на три группы:

технические Т30, предназначенные для измерения углов со средними квадратическими ошибками до ±30";

точные Т2 и Т5 – до ±2" и ±5";

высокоточные Т05 и Т1 – до ±1".

ГОСТом 10529 – 96 предусмотрена модификация точных и технических теодолитов. Так, например, теодолит Т5 должен изготовляться в двух вариантах: с цилиндрическим уровнем при алидаде вертикального круга и с компенсатором, заменяющим этот уровень. Теодолит с компенсатором при вертикальном круге должен обозначаться дополнительно буквой "К", например обозначается Т5К.

Технические и эксплуатационные характеристики теодолитов постоянно улучшаются. Шифр обновленных моделей начинается с цифры, указывающей на соответствующее поколение теодолитов: 2Т2, 2Т5К, 3Т5КП, 3Т30, 3Т2, 4Т30П и т.д.

По конструкции предусмотренной ГОСТ 10529 – 96 типы теодолитов делятся на повторительные и не повторительные.

У повторительных теодолитов лимб имеет закрепительный и наводящий винты и может вращаться независимо от вращения алидады.

Неповторительная система осей предусмотрена у высокоточных теодолитов.

Лекция 22. Основные способы измерения горизонтальных углов. Методика и точность измерения углов.

Непосредственно перед выполнением измерения теодолит приводится в рабочее положение путём последовательного выполнения трёх операций: центрирования, горизонтирования и установки трубы.

Центрирование и горизонтирование теодолита подразумевает установку осей вращения алидады в горизонтальное положение над вершиной измеряемого угла. Установка трубы – операция выставления трубы по глазу и предмету.

После установки теодолита в рабочее положение приступают к измерению горизонтальных углов. Различают следующие основные способы измерения горизонтальных углов: приемов; совмещения нулей лимба и алидады; повторений.

Способ приемов

Прием состоит из двух полуприемов. Первый полуприем выполняют при положении вертикального круга слева от зрительной трубы. Закрепив лимб и открепив алидаду, наводят зрительную трубу на правую визирную цель. После того как наблюдаемый знак попал в поле зрения трубы, зажимают закрепительные винты алидады и зрительной трубы и, действуя наводящими винтами алидады и трубы, наводят центр сетки нитей на изображение знака и берут отсчёт по горизонтальному кругу (отсчет а). Затем, открепив трубу и алидаду, наводят трубу на левую визирную цель (точка В) и берут второй отсчёт (отсчет в). Разность первого и второго отсчётов даёт величину измеряемого угла.

β = а – b

Если первый отсчёт оказался меньше второго, то к нему прибавляют 360º, тогда:

β = (а + 360°) – b

Второй полуприем выполняют при положении вертикального круга справа, для чего переводят трубу через зенит. Чтобы отсчёты отличались от взятых в первом полуприеме, смещают лимб на несколько градусов. Затем измерения выполняют в той же последовательности, как в первом полуприеме.

Если результаты измерения  угла в полуприёмах различаются не более двойной точности прибора (то есть 1'' для теодолита Т30), вычисляют среднее, которое и принимают за окончательный результат.

Способ совмещения нулей лимба и алидады

Этот способ используют, когда необходимо быстро оценить значение измеряемого угла. Совместив нули лимба и алидады, осуществляют точную наводку перекрестья нитей зрительной трубы на левую визирную цель (точка В). Закрепив лимб и открепив алидаду, визируют трубу на правую визирную цель (точка А). Отсчет по горизонтальному кругу непосредственно выразит значение измеряемого справа по ходу лежащего угла. Данный способ часто используют для быстрого контроля измерений.

Способ повторений

Способ повторений применяют, когда угловые измерения нужно выполнить с точностью более высокой, чем точность используемого прибора. Суть способа повторений заключается в последовательном многократном откладывании на лимбе измеряемого угла β.

Направив визирную ось на левую визирную цель (точка B), берут начальный отсчет по горизонтальному кругу b. Открепив алидаду, визируют прибор на правую визирную цель (точка A) без взятия отсчета, отложив тем самым первый угол β. Закрепив алидаду и открепив лимб, вновь наводят визирную ось на левую визирную цель без взятия отсчета, затем, открепив алидаду, наводят визирную ось на правую визирную цель без взятия отсчета, отложив тем самым на лимбе второй угол β, и т.д. n раз. После чего берут отсчет правой визирной цели.

Методика и точность измерения углов

Работа по измерению углов на станции выполняется в следующем порядке:

- установка теодолита в рабочее положение;

- измерение горизонтальных углов (направлений);

- обработка журнала наблюдений и контроль измерений.

Для установки теодолита в рабочее положение нужно выполнить три действия:

1 Ц е н т р и р о в а н и е. Центрирование, или установку оси вращения прибора над вершиной угла выполняют с помощью отвеса (нитяного или оптического) путем перемещения теодолита и штатива до тех пор, пока острие грузика отвеса или пересечение сетки нитей оптического отвеса не установится над вершиной угла.

2 Г о р и з о н т и р о в а н и е. Горизонтирование, или приведение оси вращения прибора в отвесное положение, выполняют следующим образом. Устанавливают уровень при алидаде горизонтального круга по направлению двух подъемных винтов и, действуя ими, приводят пузырек уровня в нуль-пункт. Затем поворачивают алидаду на 90^о, располагая ось уровня по направлению третьего подъемного винта. Вращая этот винт, вновь приводим пузырек уровня в нуль-пункт. Эти действия повторяют до тех пор, пока при повороте алидады пузырек уровня не будет отклоняться более чем на одно деление.

3 У с т а н о в к а з р и т е л ь н о й т р у б ы д л я н а б л ю д е н и й. Состоит в установке трубы по глазу и предмету. Установку трубы по глазу осуществляют вращением окулярной трубочки до тех пор, пока штрихи сетки нитей не будут видны четко. Установку трубы по предмету осуществляют вращением кремальеры (у теодолита Т-30) или фокусировочного кольца трубы (у теодолитов Т5, Т2 и т. д.) до тех пор, пока изображение предмета не получится четким.

Т о ч н о с т ь и з м е р е н и я г о р и з о н т а л ь н ы х у г л о в. На точность измерения горизонтальных  углов оказывают влияние следующие погрешности:

1) центрирования (зависит от неточности установки теодолита над точкой и длины стороны);

2) редукции (возникает из-за неточной установки визирных целей над точками);

3) визирования (зависит от точности наведения зрительной трубы на визирную цель и от увеличения зрительной трубы);

4) снятия отсчета (зависит от цены деления шкалы отсчетного устройства).

Совместное влияние перечисленных погрешностей не должно превышать двойной точности отсчетного устройства теодолита, если при измерениях не было грубых просчетов.

Лекция 23. Измерение горизонтальных углов способом приемов.

Между двумя направлениями, выходящими из общей вершины, можно измерить два угла (рис.). Обычно при съёмке измеряют углы, лежащие по ходу справа. Поэтому, зная направление хода, легко установить, какой из двух углов искомый. Направление хода задают в обозначении угла, указывая вначале заднюю точку, затем станцию (вершину угла) и переднюю точку. На местности направление от задней точки через станцию к передней точке является направлением хода, а угол, лежащий справа от этого направления, – искомым углом β.

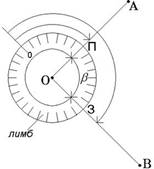
Рис. Схема измерения горизонтального угла способом приёмов

При измерении горизонтальный угол определяется как разность отсчетов по горизонтальному кругу β=З-П, где З – отсчёт по горизонтальному кругу при наблюдении задней точки (В), П – отсчет при наблюдении передней точки (А).

Так как деления на горизонтальном круге подписаны с возрастанием по часовой стрелке, то отсчет на заднюю точку должен быть всегда больше отсчета при наблюдении передней точки. В том случае, когда нулевое деление на горизонтальном круге размещается внутри измеряемого угла, отсчёт на заднюю точку будет меньше отсчёта на переднюю точку, тогда для получения величины угла к отсчету на заднюю точку необходимо добавить 360°.

В способе приемов горизонтальный угол измеряется при двух положениях вертикального круга относительно зрительной трубы, называемых полуприемами при "круге  лево" (Л) и при "круге право" (П).

Пример:

Журнал измерения углов способом приемов

Дата: 03 октября 2003 года Наблюдал: Конограй Е.

Теодолит: 2Т – 30 Записывал: Ледвягин А.

Погода: ясная

Контрольные вопросы:

1. Назначение теодолита.

2. Основные части теодолита.

3. Какие бывают отсчетные приспособления в теодолитах?

4. Назначение цилиндрического уровня при алидаде горизонтального круга.

5. Назначение зрительной трубы теодолита.

6. Характеристики зрительной трубы.

7. Какие установки зрительной трубы при наблюдениях?

Тема 1.7 Измерения превышений.

Лекция 24. Общие сведения о нивелировании. Методы и способы определения превышений.

Задачи и виды нивелирования

Нивелированием называется совокупность геодезических измерений для определения превышений между точками, а также их высот.

Нивелирование производят для изучения рельефа, определения высот точек при проектировании, строительстве и эксплуатации различных инженерных сооружений. Результаты нивелирования имеют большое значение для решения научных задач как самой геодезии, так и для других наук о Земле.

В зависимости от применяемых приборов и измеряемых величин нивелирование делится на несколько видов.

1. Геометрическое нивелирование – определение превышения одной точки над другой посредством горизонтального визирного луча. Осуществляют его обычно с помощью нивелиров, но можно использовать и другие приборы, позволяющие получать горизонтальный луч.

2. Тригонометрическое нивелирование – определение превышений с помощью наклонного визирного луча. Превышение при этом определяют как функцию измеренного расстояния и угла наклона, для измерения которых используют соответствующие геодезические приборы (тахеометр, кипрегель).

3. Барометрическое нивелирование – в его основу положена зависимость между атмосферным давлением и высотой точек на местности.

4. Гидростатическое нивелирование – определение превышений основывается на свойстве жидкости в сообщающихся сосудах всегда находиться на одном уровне, независимо от высоты точек, на которых установлены сосуды.

5. Аэрорадионивелирование - превышения определяются путем измерения высот полета летательного аппарата радиовысотомером.

6. Механическое нивелирование -  выполняется с помощью приборов, устанавливаемых в путеизмерительных вагонах, тележках, автомобилях, которые при движении вычерчивают профиль пройденного пути. Такие приборы называются профилографы.

7. Стереофотограмметрическое нивелирование основано на определении превышения по паре фотоснимков одной и той же местности, полученных из двух точек базиса фотографирования.

8. Определение превышений по результатам спутниковых измерений. Использование спутниковой системы ГЛОНАСС – Глобальная Навигационная Спутниковая Система позволяет определять пространственные координаты точек. 

Способы геометрического нивелирования

Геометрическое нивелирование – это наиболее распространенный способ определения превышений. Его выполняют с помощью нивелира, задающего горизонтальную линию визирования.

Устройство нивелира достаточно простое. Он имеет две основные части: зрительную трубу и устройство, позволяющее привести визирный луч в горизонтальное положение.

Геометрическое нивелирование можно выполнять по следующей схеме:

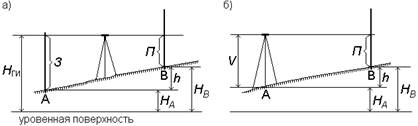
Рис.  Способы нивелирования

При нивелировании из середины нивелир располагают между двумя точками примерно на одинаковых расстояниях (рис., а). В точках устанавливают отвесно рейки с сантиметровыми делениями. Их ставят на колышек, вбитый вровень с землей, или на специальный костыль, так как рейка под собственной тяжестью будет давить на землю и отсчет по ней будет меняться. Визирный луч зрительной трубы нивелира последовательно наводят на рейки и берут отсчеты З и П, которые записывают в миллиметрах в журнал нивелирования. Отсчет по рейке производят по средней нити нивелира, т.е. по месту, где проекция средней нити пересекает рейку. Превышение между точками определяют по формуле

h = З – П

где З – отсчет назад на заднюю точку А; П – отсчет вперед на переднюю точку B.

При нивелировании вперед прибор устанавливают над точкой А (рис., б), измеряют его высоту V и берут отсчет П по рейке в точке В. Превышение определяют вычитанием из высоты прибора V отсчета П.

h = V – П.

Высоту передней точки В вычисляется по формуле:

Высоту визирного луча на уровенной поверхностью называют горизонтом инструмента H_ГИ (рис. 61) и вычисляют

Н_ГИ = Н_А + З = Н_А + V. 

Место установки нивелира называется станцией. Если для определения превышения между точками А и В достаточно установить прибор один раз, то такой случай называется простым нивелированием.

Если же превышение между точками определяют только после нескольких установок нивелира, такое нивелирование называют сложным или последовательным (рис. 62).

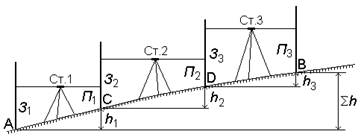
Рис. 62. Последовательное нивелирование.

В этом случае точки С и D называют связующими. Превышение между ними определяют как при простом нивелировании:

;  ;  

h = ∑З – ∑П

Такую схему нивелирования называют нивелирным ходом.

Лекция 25. Основные геодезические приборы, их устройство, поверки и порядок юстировки. Назначение нивелира.

Классификация нивелиров

Согласно действующим ГОСТам нивелиры изготавливают трех типов: высокоточные – Н-05; точные – Н-3; технические – Н-10.

В названии нивелира числом справа от буквы Н цифрой обозначают допустимую среднюю квадратическую ошибку измерения превышения на 1 км двойного нивелирного хода.

В зависимости от того, каким способом визирный луч устанавливается в горизонтальное положение, нивелиры изготавливают в двух исполнениях: - с цилиндрическим уровнем при зрительной трубе, с помощью у которого осуществляется горизонтирование визирного луча (рис. 63); - с компенсатором – свободно подвешенная оптико-механическая система, которая приводит визирный луч в горизонтальное положение. В названии нивелира буква К обозначает компенсатор (Н-3К, Н-3КЛ), где Л – лимб (рис. 64). На рис. 65 приведен технический нивелир второго поколения с компенсатором и лимбом 2Н-10КЛ

Н-3

Рис. 63. Точный нивелир Н-3 с цилиндрическим уровнем при зрительной трубе: 1 – подъемные винты; 2 – круглый уровень; 3 – элевационный винт; 4 – окуляр зрительной трубы с диоптрийным кольцом; 5 – визир; 6 – кремальера; 7 – объектив зрительной трубы; 8 – закрепительный винт; 9 – наводящий винт; 10 – контактный цилиндрический уровень; 11 – юстировочные винты цилиндрического уровня

 Нивелирные рейки

Нивелирные рейки для нивелирования III – IV класса и технического изготавливают из деревянных брусьев двутаврового сечения шириной 8 – 10 и толщиной 2 – 3 см.

Рейка РН-3 (рис. 66) имеет длину 3 м. Деления нанесены через 1 см. Нижняя часть рейки заключена в металлическую оковку и называется пяткой.

Основная шкала имеет деления черного и белого цвета, ноль совмещен с пяткой рейки. Дополнительная шкала на другой стороне рейки имеет чередующиеся красные и белые деления. С пяткой рейки совмещен отсчет больше 4000 мм. Часто встречаются комплекты реек, у которых с пятками красных сторон совпадают отсчеты 4687 и 4787 мм. Поэтому превышения, измеренные по красным сторонам реек, будут больше или меньше на 100 мм измеренных по черным сторонам реек.

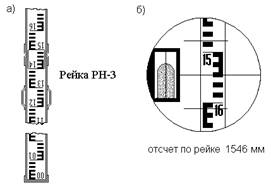
Рис. 66. Нивелирная рейка (а) и поле зрения зрительной трубы нивелира с цилиндрическим уровнем (б)

Для установки нивелира в рабочее положение его закрепляют на штативе и, действуя тремя подъемными винтами, приводят пузырек круглого уровня в центр ампулы. При этом ось вращения нивелира занимает отвесное положение. Наведение зрительной трубы на рейку осуществляют вначале вручную с помощью визира, а затем зажимают закрепительный винт зрительной трубы и наводящим винтом выполняют точное визирование на рейку. Резкость изображения сетки нитей достигается вращением окулярного кольца, а резкость изображения рейки – вращением винта кремальеры. Сетка нитей имеет вертикальный штрих и три горизонтальных, верхний и нижний являются нитяным дальномером.
Перед каждым отсчетом по рейке визирную ось нивелира приводят в горизонтальное положение, добиваясь совмещения изображения концов пузырька цилиндрического уровня в поле зрения зрительной трубы путем вращения элевационного винта.
Отсчет по рейке состоит из четырех цифр и выражает расстояние от измеряемой точки до визирной оси нивелира в миллиметрах. Выполняют отсчет по среднему горизонтальному штриху сетки нитей. Отсчет по рейке берут от меньшего к большему числу. Обратите внимание на то, что изображение в зрительной трубе обратное, следовательно, отсчеты возрастают сверху вниз.
Первые две цифры отсчета, обозначающие дециметры, подписаны на рейке, они видны в зрительной трубе вблизи среднего горизонтального штриха.
Третья цифра считается по числу сантиметровых шашек от начала дециметрового деления (от верхней части знака символа Е вниз) до среднего горизонтального штриха сетки нитей.

Четвертая цифра, обозначающая миллиметры, по рейке оценивается на глаз.

Контрольные вопросы:

1. Что называется нивелированием?

2. Назовите виды нивелирования?

3. Назовите способы геометрического нивелирования?

4. В чем заключается способ нивелирования из середины и вперед?

5. В чем сущность последовательного нивелирования?

6. В чем сущность тригонометрического, барометрического и гидростатического нивелирования?

7. Как нивелиры классифицируются по точности?

8. Чем отличается уровенный нивелир от нивелира с компенсатором?

9. Когда можно не учитывать поправки за кривизну Земли и рефракцию при геометрическом нивелировании?  

Список используемой литературы

1.            «Геодезия», Киселев М.И., Михелев Д.Ш. Академия,2008 год

2.            «Геодезия и топография»,       Курошев Г.Д., Смирнов Л.Е. Академия,2008 год

3.            «Геодезия»  Маслов А.В., Гордеев А.В., Батраков Ю.Г.       Москва, Колос, 2006 год

4.            «Геодезия»  Поклад Г.Г., Гринев С.П.      Москва, «Академический проект», 2008 год

5.            «Практикум по геодезии»        Поклад Г.Г., Гринев С.П.      Москва, «Академический проект», 2011 год

6.            «Практикум по геодезии»        В.Г.Селиханович, В.П.Козлов,

7.            Г.П. Логинова       Москва, 2006г.

8.            «Основы геодезии и картографии»   Новиков В.И., Рассода А.Б.   Саратов, 2007 г.

9.            www.geod-ref.ru

Скачано с www.znanio.ru