В этой статье вы узнаете

•      Как решать квадратные уравнения?

•      Сколько существует способов решения квадратных уравнений?

•      Какие квадратные уравнения с параметром могут попасться на ОГЭ и ЕГЭ?

Числа a, b и c называются коэффициентами уравнения. Выражение:

a𝑥²+bx+c, в котором a≠0, называется квадратным трехчленом. 

 Если D>0, то уравнение имеет два корня:                                                                                   ;

•     

•      Если D<0, не имеет корней: x∈∅.

Примеры

1.    𝑥²-5x-6=0

D=𝑏² − 4𝑎𝑐=(−5)² − 4 ∗ 1 ∗ (−6) = 25 + 24 = 49

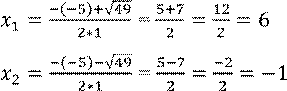
Ответ: -1;6

2.    𝑥²-12x+36=0

D=𝑏² − 4𝑎𝑐=(−12)² − 4 ∗ 1 ∗ 36 = 144 − 144 = 0

Ответ: 6

3. 𝑥²-10x+26=0

D=𝑏² − 4𝑎𝑐=(−10)² − 4 ∗ 1 ∗ 26 = 100 − 104 =−4

Ответ: нет корней

Теорема Виета

Оказывается, корни квадратного уравнения связаны с его коэффициентами весьма простыми соотношениями.

−𝑏

𝑥₁+𝑥₂ =

{     𝑐𝑎 𝑥₁∗𝑥₂ =

𝑎

Пример

                 1. 𝑥²-3x+2=0                                                                 2. 2𝑥²-5x+3=0

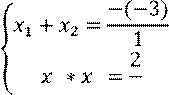
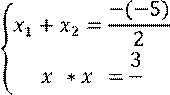                                 1           2                                                                                                                       1           2

                                                           1                                                                               2

                  𝑥₁ = 1; 𝑥₂ = 2                                                             𝑥₁ = 1; 𝑥₂ = 1,5

                Ответ: 1;2                                                                     Ответ: 1;1,5

a𝑥²+bx+c=0

1. Если a+b+c=0, то  2. Если a+c=b, то  

Примеры

Неполное квадратное уравнение – это уравнение, в котором хотя бы один из коэффициентов b и c равны 0.

 Если b = 0, то уравнение имеет вид: a𝑥²+c=0:

𝒙^𝟐-4=0 4 способа решения:

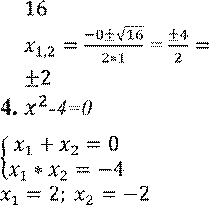𝑥₁ = 2

𝑥₂ = −2

2. 𝑥²-4=0

(x-2)(x+2)=0

Произведение равно нулю, когда хотя бы один из множителей равен нулю. x-2=0 или x+2=0

 Если с = 0, то уравнение имеет вид: a𝑥²+bx=0:

𝒙^𝟐-4x=0

3 способа решения:

1.   𝑥²-4x=0 x(x-4)=0

Вынесем общий множитель за скобки

Произведение равно нулю, когда хотя бы один из множителей равен нулю. x=0 или x-4=0

                        𝑥₁=0       𝑥₂=4

2.   𝑥²-4x=0

D=(−4)² − 4 ∗ 1 ∗ 0 = 16

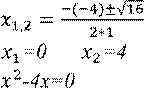
3.

{𝑥1 + 𝑥₂ = 4

𝑥₁ ∗ 𝑥₂ = 0 𝑥₁ = 0; 𝑥₂ = 4

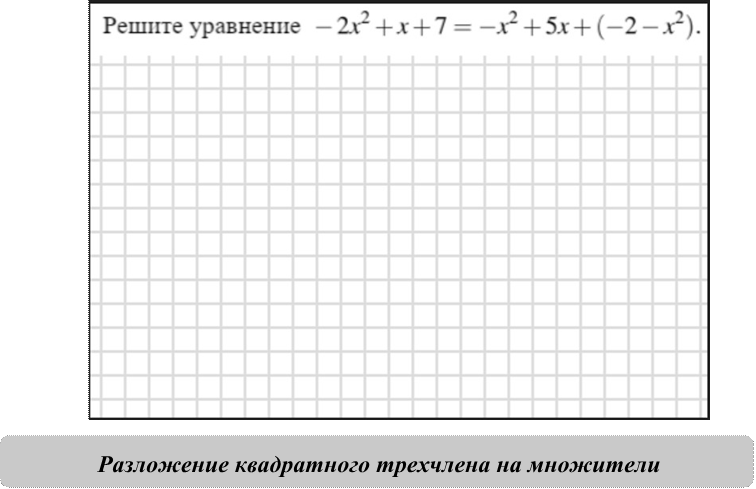
                                                                    a𝑥²+bx+c=𝑎(𝑥 − 𝑥₁)(𝑥 − 𝑥₂)

Задание: Найдите все значения параметра 𝒂 при каждом из которых уравнение (𝒂 − 𝟑)𝒙^𝟐 − 𝟐𝒂𝒙 − 𝟏 = 𝟎 имеет ровно один корень.