
ЛАБОРАТОРНАЯ РАБОТА № 1. «РЕШЕНИЕ одноиндексных ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
С ИСПОЛЬЗОВАНИЕМ Microsoft Excel»
1. 1 ЦЕЛЬ РАБОТЫ
Приобретение навыков решения одноиндексных задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
1.2 ОСНОВНЫЕ ПОЛОЖЕНИЯ
Если в какой-либо системе (экономической, организационной, военной и т.д.) не хватает имеющихся в наличии ресурсов для эффективного выполнения каждой из намеченных работ, то возникают так называемые распределительные задачи. Цель решения распределительной задачи – отыскание оптимального распределения ресурсов по работам. Под оптимальностью распределения может пониматься, например, минимизация общих затрат, связаных с выполнением работ, или максимизация получаемого в результате общего дохода.
Для решения таких задач используются методы математического программирования. Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования.
Характерные черты задач ЛП следующие:
1) показатель
эффективности L представляет собой линейную
функцию, заданную на элементах решения ![]() ;
;
2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
В общей форме записи модель задачи ЛП имеет вид:
|
целевая функция (ЦФ)
при ограничениях
|
Допустимое
решение – это
совокупность чисел ![]() , удовлетворяющих ограничениям
задачи.
, удовлетворяющих ограничениям
задачи.
Оптимальное
решение – это план
![]() , при
котором ЦФ принимает свое максимальное (минимальное) значение.
, при
котором ЦФ принимает свое максимальное (минимальное) значение.
1.3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели ЛП, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
1.3.1 ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel
ДЛЯ РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ ЛП [5]
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1 Ввести условие задачи:
а) создать экранную форму для ввода условия задачи:
§ переменных,
§ целевой функции (ЦФ),
§ ограничений,
§ граничных условий;
b) ввести исходные данные в экранную форму:
§ коэффициенты ЦФ,
§ коэффициенты при переменных в ограничениях,
§ правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
§ формулу для расчета ЦФ,
§ формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
§ целевую ячейку,
§ направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
§ ячейки со значениями переменных,
§ граничные условия для допустимых значений переменных,
§ соотношения между правыми и левыми частями ограничений.
2 Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
1.3.1.1.Пример решения одноиндексной задачи ЛП
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
|
|
(1.1) |
ВВОД ИСХОДНЫХ ДАННЫХ
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
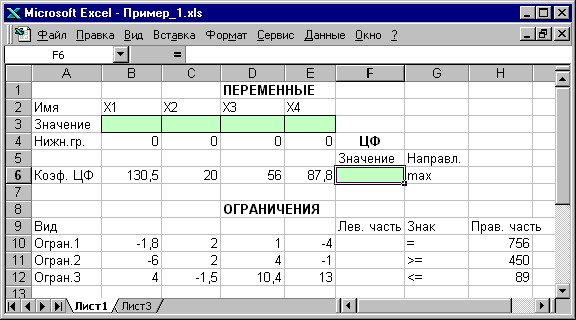
Рис. 1.1. Экранная форма задачи (1.1) (курсор в ячейке F6)
В
экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи
поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и
цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП.
Так, например, переменным задачи (1.1) соответствуют ячейки B3 (![]() ), C3
(
), C3
(![]() ),
D3 (
),
D3 (![]() ), E3 (
), E3 (![]() ),
коэффициентам ЦФ соответствуют ячейки B6 (
),
коэффициентам ЦФ соответствуют ячейки B6 (![]() 130,5), C6
(
130,5), C6
(![]() 20),
D6 (
20),
D6 (![]() 56), E6 (
56), E6 (![]() 87,8),
правым частям ограничений соответствуют ячейки H10 (
87,8),
правым частям ограничений соответствуют ячейки H10 (![]() 756), H11 (
756), H11 (![]() 450), H12 (
450), H12 (![]() 89) и т.д.
89) и т.д.
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
|
|
(1.2) |
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
|
|
(1.3) |
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
|
=СУММПРОИЗВ(B$3:E$3;B6:E6), |
(1.4) |
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
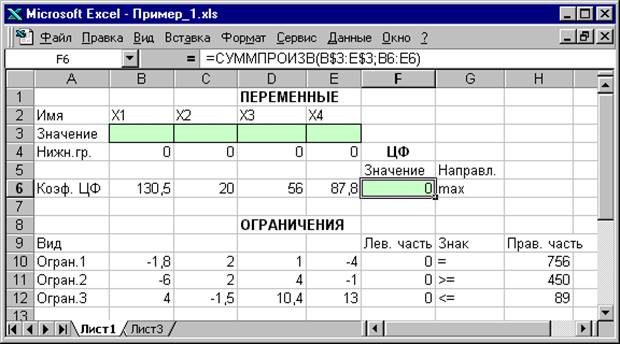
Рис. 1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул
(курсор в ячейке F6)
Примечание
1.1. Существует
другой способ задания функций в Excel
с помощью режима «Вставка функций», который можно вызвать из меню
«Вставка» или при нажатии кнопки «![]() « на
стандартной панели инструментов. Так, например, формулу (1.4) можно задать
следующим образом:
« на
стандартной панели инструментов. Так, например, формулу (1.4) можно задать
следующим образом:
§ курсор в поле F6;
§
нажав кнопку «![]() »,
вызовите окно «Мастер функций – шаг 1 из 2»;
»,
вызовите окно «Мастер функций – шаг 1 из 2»;
§ выберите в окне «Категория» категорию «Математические»;
§ в окне «Функция» выберите функцию СУММПРОИЗВ;
§ в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение B$3:E$3, а в строку «Массив 2» – выражение B6:E6 (рис.1.3);
§ после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
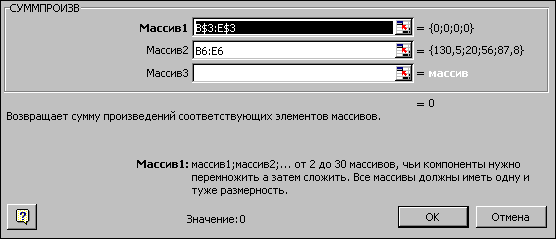
Рис. 1.3. Ввод формулы для расчета ЦФ в окно «Мастер функций»
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.
Таблица 1.1
Формулы, описывающие ограничения модели (1.1)
|
Левая часть ограничения |
Формула Excel |
|
|
=СУММПРОИЗВ(B$3:E$3;B10:E10) |
|
|
=СУММПРОИЗВ(B$3:E$3;B11:E11) |
|
|
=СУММПРОИЗВ(B$3:E$3;B12:E12) |
Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
§ поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
§ помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
§ на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).
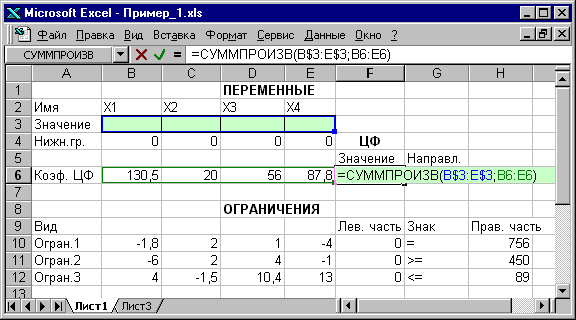
Рис. 1.4. Проверка правильности введения формулы в целевую ячейку F6
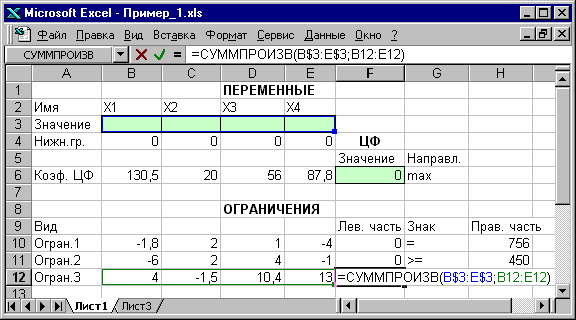
Рис. 1.5. Проверка правильности введения формулы в ячейку F12
для левой части ограничения 3
Задание ЦФ
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
§ поставьте курсор в поле «Установить целевую ячейку»;
§ введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме - это будет равносильно вводу адреса с клавиатуры;
§ введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
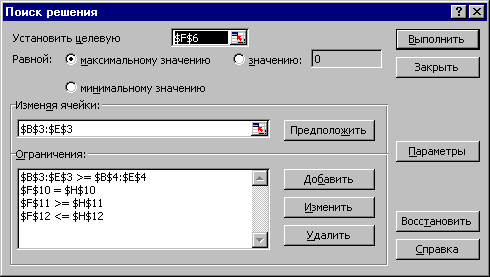
Рис. 1.6. Окно «Поиск решения» задачи (1.1)
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $B$3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
§ Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис.1.7).
§ В поле «Ссылка на ячейку» введите адреса ячеек переменных $B$3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
§
В поле знака
откройте список предлагаемых знаков и выберите ![]() .
.
§ В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $B$4:$E$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
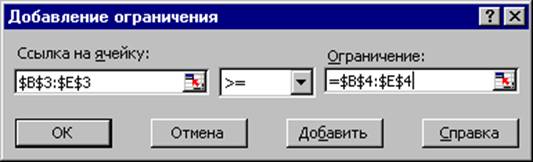
Рис. 1.7. Добавление условия неотрицательности переменных задачи (1.1)
Задание знаков ограничений ![]() ,
, ![]() , =
, =
· Нажмите кнопку «Добавить» в окне «Добавление ограничения».
· В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
· В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
· В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $H$10.
· Аналогично введите ограничения: $F$11>=$H$11, $F$12<=$H$12.
· Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
РЕШЕНИЕ ЗАДАЧИ
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
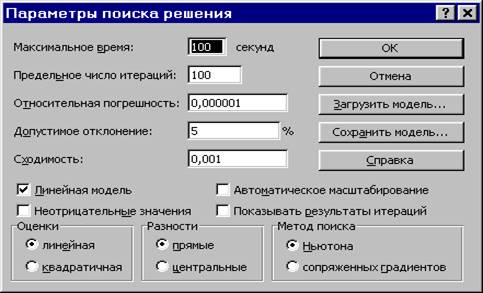
Рис. 1.8. Параметры поиска решения, подходящие для большинства задач ЛП
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «OK».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи ЛП на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.
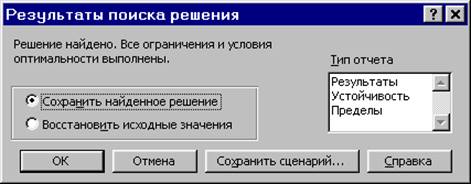
Рис. 1.9. Сообщение об успешном решении задачи
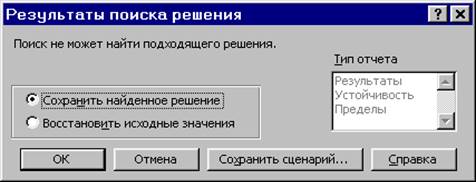
Рис. 1.10. Сообщение при несовместной системе ограничений задачи
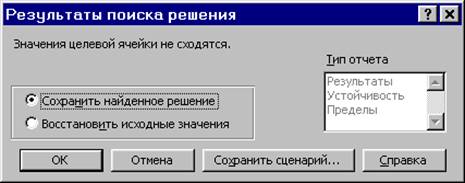
Рис. 1.11. Сообщение при неограниченности ЦФ в требуемом направлении
Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при решении задачи ЛП выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel. Поэтому, прежде чем делать вывод о принципиальной невозможности нахождения оптимального решения задачи, проверьте: не было ли допущено ошибок по ходу выполнения задания?
В том случае, когда при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «OK». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
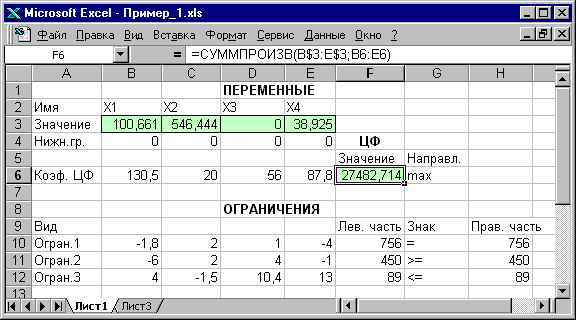
Рис. 1.12. Экранная форма задачи (1.1) после получения решения
1.3.1.2 Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
· В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
· В окне «Поиск решения» (меню «Сервис»®«Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис. 1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $B$3:$E$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «OK».
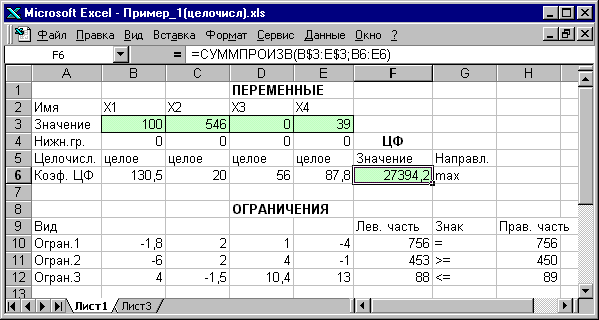
Рис. 1.13. Решение задачи (1.1) при условии целочисленности ее переменных
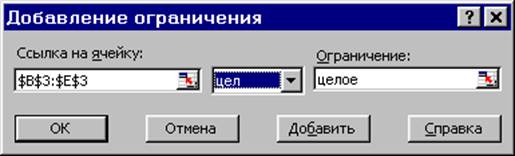
Рис. 1.14. Ввод условия целочисленности переменных задачи (1.1)
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
1.4 СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать титульный лист, номер варианта, все необходимые промежуточные таблицы Microsoft Excel и результаты решения задачи. Обязательно наличие выводов по проделанной работе. В случае несвоевременного выполнения задания к отчету прилагается дискета с выполненным заданием.
1.5 КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Что такое «математическое программирование?»
2 Что значит «оптимальное решение»?
3 Каковы основные этапы решения задач ЛП в MS Excel?
4 Каков вид и способы задания формул для целевой ячейки и ячеек левых частей ограничений?
5 Почему при вводе формул в ячейки ЦФ и левых частей ограничений в них отображаются нулевые значения?
6 Каким образом в MS Excel задается направление оптимизации ЦФ?
7 Как наглядно отобразить в экранной форме ячейки, используемые в конкретной формуле, с целью проверки ее правильности?
8 Поясните общий порядок работы с окном «Поиск решения».
9 Каким образом можно изменять, добавлять, удалять ограничения в окне «Поиск решения»?
10 Какие сообщения выдаются в MS Excel в случаях: успешного решения задачи ЛП; несовместности системы ограничений задачи; неограниченности ЦФ?
11 Объясните смысл параметров, задаваемых в окне «Параметры поиска решения».
12 Каковы особенности решения в MS Excel целочисленных задач ЛП?
1.6 ЗАДАНИЯ
Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл.1.2).
Таблица 1.2
Варианты задач к лабораторной работе № 1
|
№ варианта |
Математическая модель |
||
|
1 |
|
||
|
2 |
|
||
|
3 |
|
||
|
4 |
|
||
|
5 |
|
||
|
6 |
|
||
|
8 |
|
|
||
|
9 |
|
|
||
|
10 |
|
|
||
|
11 |
|
|
||
|
12 |
|
|
||
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.