ЛАБОРАТОРНАЯ РАБОТА № 2
Разработка алгоритмов и программ разветвляющейся структуры
Цель: освоить методы разработки алгоритмов и программирования задач разветвляющейся структуры.
Краткие теоретические сведения
Решение абсолютного большинства задач невозможно свести к алгоритмам линейной структуры. Часто в зависимости от каких-либо промежуточных результатов или исходных данных вычисления осуществляются либо по одним, либо по другим формулам, то есть в зависимости от выполнения некоторого логического условия вычислительный процесс осуществляется по одной или другой ветке. Такие задачи можно описать с помощью алгоритмов разветвляющейся структуры.
Алгоритм разветвляющейся структуры – это алгоритм, в котором осуществляется проверка какого-либо условия и в зависимости от результата проверки выбирается один из нескольких возможных путей вычислительного процесса. Каждый подобный путь называется ветвью алгоритма.
В блок-схемах разветвляющийся вычислительный процесс может изображаться в двух формах: полной и неполной.
 |
|||
 |
|||
Полная форма:
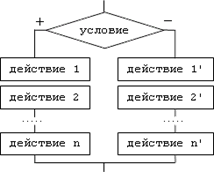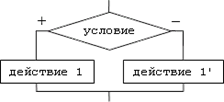Неполная форма:
19
Пример 1. Вычислить значение переменной Z, используя формулы:
ìsin(x),
ï
ícos(x),
ïtg (x),
если если если
x £ a
a x b x ³ b
Из математической формулировки задачи видно, что вычислительный процесс имеет три ветви. С помощью условного блока проверяется выполнение только одного условия, по которому выбирается выражение для реализации одной ветви. Поэтому для определения того, по какой из двух оставшихся ветвей должен идти вычислительный процесс после невыполнения первого условия, необходимо использовать еще один условный блок. После вычисления переменной по формуле осуществляется переход в общую ветку к блоку вывода.
Схема алгоритма решения задачи имеет вид:
Пример 2. Вычислить значение переменной Z, используя формулы:
z = x ,
y
20
где
y = sin(nx) + 0,5
Казалось бы, что решение этой задачи описывает алгоритм линейной структуры. Однако для удовлетворения свойства массовости и результативности алгоритма необходимо, чтобы при различных исходных данных был получен числовой результат или сообщение о том, что задача не может быть решена при заданных исходных данных. Действительно, если у = 0, то задача не может быть решена, поскольку делить на ноль нельзя. Поэтому в алгоритме необходимо предусмотреть проверку условия и выдать как результат информацию о том, что у = 0.
Схема алгоритма решения задачи имеет вид:
Для организации разветвленных вычислительных процессов в программах используются операторы безусловного перехода, условий и выбора.
Оператор безусловного перехода имеет вид:
Goto метка;
Оператор безусловного перехода – это оператор, который передает управление в программе другому оператору, перед которым стоит метка, указанная в операторе Goto.
Метка - это произвольный идентификатор (имя) или целое число без знака, которая должна быть объявлена в разделе описания Label. Отделяется метка от оператора двоеточием.
21
Условный оператор If ... Then ... Else является простой формой проверки условий и имеет следующий синтаксис:
If условие Then оператор 1 Else оператор 2;
Оператор 1 выполняется в том случае, если условие истинно, иначе выполняется оператор 2. Условие - это выражение логического типа.
В условном операторе допустимо использование составного оператора. Составной оператор - это объединение нескольких операторов в одну группу. Форма записи данного оператора имеет вид:
If условие Then Begin
оператор 1;
…. оператор n
Else
End
Begin
оператор 1;
…. оператор n
End;
В этой форме записи условного оператора служебные слова Begin и End называются операторными скобками. Составной оператор используется в тех случаях, когда по правилам языка программирования Pascal разрешается использовать только один оператор, а программисту для решения задачи необходимо выполнить группу операторов.
Поскольку ветвь Else является необязательной, условный оператор может быть записан в краткой форме:
If условие Then Begin
оператор 1;
…. оператор n
или
22
End;
If условие Then оператор;
Оператор выбора Case, который позволяет выбрать и выполнить один оператор, имеет следующий вид:
Case выражение of
список меток 1 : оператор 1;
список меток 2 : оператор 2;
……………..
список меток N : оператор N;
else
end;
оператор
Выражение – это выражение порядкового типа, определяющее дальнейший ход выполнения программы. Не может принимать значение действительного числа или строки. Список меток представляет собой список констант, разделенных запятыми, если диапазон чисел - то указывают первую и последнюю константы диапазона, разделенные двумя точками. Например, список 1, 2, 3, 4 можно записать как список 1 .. 4.
Выполняется оператор Case следующим образом: вычисляется значение выражения (за служебным словом Case), затем полученное значение последовательно сравнивается с константами из списка меток, стоящих перед двоеточием. Если значение выражения совпадает с константой из какого-либо списка меток, то выполняется соответствующий этому списку меток оператор. Если значение выражения не совпадает ни с одной константой из всех списков, то выполняется оператор, стоящий за словом else. Раздел else является необязательным.
Например, вывести на экран название времени года, в зависимости от введенного номера месяца
case n of
3..5 : s:=‟vesna‟;
6..8 : s:=‟leto‟;
9..11 : s:= „osen‟; else
s:=‟zima‟; end;
23
Пример 3. Вычислить значение переменной t, используя формулы:
ì
t = í
2x - p ,
если
x < a
Решение.
Исходные данные: x, a.
îln x,
если
x ³ a
Результат вычислений: значение t. Ограничения:
1. для вычисления переменной t по формуле соответствующей условию х<а необходимо дополнительно проверить условие 2х-p³0, иначе вывести сообщение «корень не вычисляется»;
2. для вычисления переменной t по формуле соответствующей условию х³а необходимо дополнительно проверить условие х>0, иначе вывести сообщение «логарифм не вычисляется».
Схема алгоритма решения задачи имеет вид:
Текст программы решения задачи имеет вид: Program rabota;
Label 1;
Var x, a, t: real; begin
writeln („Ввод x, a‟); readln (x, a); If x < а Then
24
If 2 * x - pi >= 0 Then t: = Sqrt(2 * x - pi)
Else begin writeln („Корень не вычисляется‟); goto 1 end Else
If x > 0 Then t: = Ln(x)
Else begin writeln („ln не вычисляется‟); goto 1 end; Writeln ('При х=‟, x:6:2, „ a=‟, a:6:2, „ t=‟, t:6:2);
1: end.
Задание
1. Изучить лекционный материал и методические рекомендации для выполнения задания.
2. Разработать алгоритм для расчета заданной переменной.
3. Составить программу на алгоритмическом языке Pascal.
4. Выполнить отладку и тестирование программы на компьютере.
5. Подготовить отчет о выполнении задания. Пример оформления отчета представлен в приложении 2.
6. Подготовить ответы на контрольные вопросы.
Варианты заданий
|
№ п/п |
Вид задания |
|
№ п/п |
Вид задания |
|
1 |
ìa + ln(x + a), если 0 £ x £ 2 y = ï sin(ax) , если x > 2 í ïx2 - cos a, если x < 0 î |
|
2 |
ìln x + b , если x < 4 ï z = í(1 + x2 ) × b, если 4 £ x £ 5 ïb × e-x , если x > 5 î |
|
3 |
ìb 2 - x + b, если x < 2 v = ï bx -1 í , если x ³ 2 ïln(x - b) î |
|
4 |
ì1.5 × t 2 z = ï2a - x + b, если x < 3 í ïî5t + bx - cos2 a, если x ³ 3 |
|
5 |
ìln x 3 - b3 , если x < 1 z = ï í sin x + b ï , если x ³ 1 î x - b |
|
6 |
ìc + x2 a = ï 2 - x , если x £ 4 í ï cx3 + x - c , если x > 4 î |
25
|
7 |
ìab(x + x2 ), если x < -1.2 ï a - b y = ï , если -1.2 £ x £ 1.1 í1 + x ï îï(a + b) × tgx, если x > 1.1 |
|
8 |
ì x - c , если x < 0 ï 2 y = ï in(x + c), если 0 £ x £ 0.5 ís ï3 + c ï , если x > 0.5 î ln x |
|
9 |
ì3 ax +1, если x > 1.5 z = ïax +1 í îï sin x , если x £ 1.5 |
|
10 |
ìsin(z × a), если z > 0 y = ï cos z í ï , если z £ 0 î ln a |
|
11 |
z = ì1.5a - ln(x - a), если x £ 2 í î 8.5 - xa , если x > 2 |
|
12 |
p = ìïsin(x + a), если x ³ a í ïî3 ln(x - a), если x < a |
|
13 |
ì1+ sin3 x, если x > 1.5 a = ï íï 1 , если x £ 1.5 î1- x2 |
|
14 |
ì 1 y = ïe x-1 , если x < 2 í îï3 x 2 - 4, если x ³ 2 |
|
15 |
ì t × e -x y = ïln(x +1) , если x < 1 í ïsin x + t 2 , если x ³ 1 î |
|
16 |
ìsin(x + a), если x ³ 2 y = ïa - x íï , если x < 2 î x |
|
17 |
ì a + bx , если x < -2 y = ïa + bx, если - 2 £ x £ 0 í ï(a - b) × cos x, если x > 0 î |
|
18 |
ì y + 3 ax, если x < 0 v = ï y + x í , если x ³ 0 ïln(x - y) î |
|
19 |
ìsin x, если x < 1 y = ï a - x , если 1 £ x £ 2 í ïcos 3 x, если x > 2 î |
|
20 |
ìz - ab, если z < 0 y = ï + az, если 0 £ z < 1 íbz ï îab + 3 1- z , если z ³ 1 |
|
21 |
ìln ax +1, если x < -0.5 ï y = í ax , если - 0.5 £ x £ 2 ïax 3 +1, если x > 2 î |
|
22 |
ì 1 ït - ln(t - a) , если t £ 2 z = ï í x ïcos 2 , если t > 2 î a |
|
23 |
ìex × ab, если x < -0.1 ï 1 y = ï , если - 0.1 £ x £ 0.3 ísin x ï ïîax2 + b, если x > 0.3 |
|
24 |
ì x ïtg p , если - 1 £ x £ 1 ï t = íe-x + 3 x , если x > 1 ïx ln b, если x < -1 ï î |
26
|
25 |
ì ïsin 2 x, если x £ 0 y = ï os x 3 , если 0 < x £ 0.5 íc ïcos x ï , если x > 0.5 î ln x |
|
26 |
ì ïln(xy), если x < -1 z = ï x , если x > 1 íe ï 1 , если -1 £ x £ 1 ï x î |
|
27 |
ì a + bx , если x < 0.3 ï ln x ï z = ía x + b2, если 0.3 £ x £ 0.6 ïbx2, если x > 0.6 ï î |
|
28 |
ìcos3 x, если x > 1 ï q = í b - x2 , если -1 £ x £ 1 ï x , если x < -1 î |
|
29 |
ìcos(xa), если x < a f = ï - 2bx í1 , если x ³ a ï ln x î |
|
30 |
ì5 ax -1, если x < 5 s = ï í 2.5 , если x ³ 5 ïln( x - a) î |
Контрольные вопросы
1. Что такое алгоритм?
2. Какими свойствами обладает алгоритм?
3. Какие формы используются для описания алгоритма?
4. Какие геометрические фигуры могут использоваться в блок- схеме разветвляющегося алгоритма?
5. Каковы типовые структуры алгоритма?
6. Какова структура программы?
7.Какие разделы описаний используются при программировании разветвляющегося алгоритма?
8. Какова структура условного оператора?
9. Какие существуют формы записи условного оператора?
10. Что такое составной оператор? Привести примеры его использования.
11. Какой оператор позволяет вывести на экран текстовое сообщение?
12. Что такое метка? Привести примеры ее использования.
13. Какой оператор позволяет передать управление другому оператору в программе?
Скачано с www.znanio.ru
ЛАБОРАТОРНАЯ РАБОТА № 2
Пример 1
Казалось бы, что решение этой задачи описывает алгоритм линейной структуры
Условный оператор If ... Then
Оператор выбора Case , который позволяет выбрать и выполнить один оператор, имеет следующий вид:
Пример 3
If 2 * x - pi >= 0
7 ì ab ( x + x 2 ), если x < - 1.2 ï a - b y = ï , если - 1.2…
Контрольные вопросы 1.
© ООО «Знанио»
С вами с 2009 года.
