1.  ИНФОРМАТИКА И ИНФОРМАЦИЯ

 

Содержание:



1. Введение в информатику. Информатика как наука 2. Понятие информации 3. Формы представления информации, виды и  свойства 4. Кодирование информации 5. Системы счисления 6. Двоичная арифметика 7. ЭВМ и двоичная система счисления 8. Азбука машинной логики. Логические операции, элементы и функции 9. Булевы выражения и законы алгебры логики

 

Основные понятия:

Информация – сведения, снимающие неопределенность об окружающем мире, которые являются объектом хранения, преобразования, передачи и использования. Сведения - это знания, выраженные в сигналах, сообщениях, известиях, уведомлениях и т.д.

Информатика - одна из фундаментальных отраслей научного знания, формирующая системно-информационный подход к анализу окружающего мира, изучающая информационные процессы, методы и средства получения, преобразования, передачи, хранения и использования информации.

Информационные технологии — методы и средства накопления, об­работки и передачи информации с использованием определенных технических средств.

Новые информационные технологии — технологии накопле­ния, обработки и передачи информации с использованием ЭВМ.

Информационные процессы — процессы передачи, накопле­ния и переработки информации в общении людей, в живых орга­низмах, технических устройствах и т.д.

Система счисления ­– совокупность приемов наименования и обозначения чисел.

Основание системы счисления – количество различных цифр, используемых для изображения чисел в позиционной системе счисления.

 

1. Введение в информатику. Информатика как наука

Фундаментальной чертой цивилизации является рост  производства, потребления и накопления информации во всех отраслях человеческой деятельности.  Вся  жизнь человека так или иначе связана с получением,  накоплением и обработкой информации.  Что бы человек ни делал: читает ли книгу, смотрит ли телевизор, разговаривает ли - он постоянно и непрерывно получает и обрабатывает  информацию.

Для нашего века – века автомобиля, электричества, авиации, атомной энергии, космонавтики, электронной техники – характерна небывалая скорость развития науки, техники и новых технологий. Так, от изобретения книгопечатания (середина XV века) до изобретения радиоприемника (1895 год) прошло около   440 лет, а между изобретением радио и телевидения – около 30 лет.  Разрыв  во  времени между изобретением транзистора и интегральной схемы составил всего 5 лет.

В области накопления научной информации ее объем, начиная с XVII века, удваивался примерно каждые 10–15 лет. Поэтому одной из важнейших  проблем  человечества является лавинообразный поток информации в любой области его жизнедеятельности. Подсчитано, например, что в настоящее время специалист должен тратить около 80%  своего рабочего времени, чтобы уследить за всеми новыми печатными работами в его области деятельности. Увеличение информации и растущий спрос на нее обусловили появление отрасли, связанной с автоматизацией обработки информации - ИНФОРМАТИКИ.

 

G

Информатика – научная дисциплина, изучающая структуру и общие свойства информации, а также закономерности всех процессов обмена информацией от непосредственного устного и письменного общения специалистов до формальных процессов обмена посредством различных носителей информации. Значительную часть этих процессов составляет научно-информационная деятельность по сбору, переработке, хранению, поиску и распространению информации.

Объектом изучения информатики не является содержание конкретной научно-информационной деятельности, которой должны заниматься специалисты в соответствующих отраслях науки и техники. Она изучает внутренние механизмы реферирования документов на естественных языках, разрабатывает общие методы такого реферирования.

Основная задача информатики заключается в определении общих закономерностей, в  соответствии с которыми происходит создание новой информации, ее преобразование, передача и использование в различных сферах деятельности человека. Прикладные задачи заключаются в разработке более эффективных методов и средств осуществления информационных процессов, в определении способов оптимальной научной коммуникации  с широким применением технических средств.

 Информатика исследует следующие группы основных вопросов:

Ø технические,  связанные  с изучением методов и средств надежного сбора, хранения, передачи, обработки и выдачи информации;

Ø семантические, определяющие способы описания смысла информации, изучающие языки ее описания;

Ø прагматические, описывающие методы кодирования информации;

Ø синтаксические, связанные с решением задач по формализации и автоматизации некоторых видов научно-информационной деятельности, в частности, индексирование, автоматическое реферирование, машинный перевод.

Информатика как понятие прочно вошло в нашу жизнь, стало одним из синонимов научно-технического прогресса.  Слово это появилось в начале 60-х годов во французском языке для обозначения автоматизированной обработки информации в обществе.

 

G

Информатика (от французского information – информация и automatioque – автоматика) – область научно-технической деятельности, занимающаяся исследованием процессов получения, передачи, обработки, хранения, представления информации, решением проблем создания, внедрения и использования информационной техники и технологии во всех сферах общественной жизни; одно из главных направлений научно-технического прогресса.

 

В некоторых более кратких определениях информатика трактуется как особая наука о законах и методах получения и  измерения, накопления и хранения, переработки и передачи информации с применением математических и технических средств. Однако все имеющиеся определения отражают наличие двух главных составляющих информатики - информации и соответствующих средств ее обработки.

Становление и бурный прогресс информатики обусловлены резким ростом масштабов, сложности и динамизма общественной практики - объектов исследования, систем управления, задач проектирования и т.д. Дальнейшее развитие многих областей науки, техники и производства потребовало количественного и качественного роста возможностей переработки информации, существенного усиления  интеллектуальной деятельности человека. Информационные ресурсы общества приобрели на современном этапе стратегическое значение. Огромную, по существу, революционизирующую роль в становлении и развитии информатики сыграло создание электронно-вычислительной машины (ЭВМ) и современной компьютерной техники, ставшее одним из ключевых направлений научно-технического прогресса, подлинным его катализатором.

В структуре информатики как науки выделяют алгоритмическую, программную и техническую области. Смежными дисциплинами с информатикой являются кибернетика и вычислительная техника, которые во многих случаях решают общие задачи, связанные с переработкой информации.

Стержневым направлением и предметом информатики является разработка автоматизированных информационных технологий на основе использования ЭВМ.  Академик А.П.Ершов называл информатику наукой "о рациональном использовании  ЭВМ для решения различных  задач". К числу основных особенностей информатики относят ее высокую наукоемкость, использование новейших достижений различных наук - математики, семиотики, теории моделирования, теории алгоритмов и др. Информатике присущ высокий динамизм, активное влияние на развитие научно-технического прогресса, широкий диапазон сфер практического использования в управлении, производственной деятельности, образовании, здравоохранении, науке, культуре и т.д., высокая эффективность применения, быстрота окупаемости расходов на внедрение новых информационных технологий на базе компьютерной техники.

Применение электронно-вычислительных машин послужило основой для создания новой информационной технологии, позволяющей не только накапливать, хранить, перерабатывать информацию, но и получать новую информацию, новые знания. В этом состоит коренное отличие возможностей ЭВМ от возможностей любой другой  информационной техники - средств связи, проекционной аппаратуры, телевидения и др.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

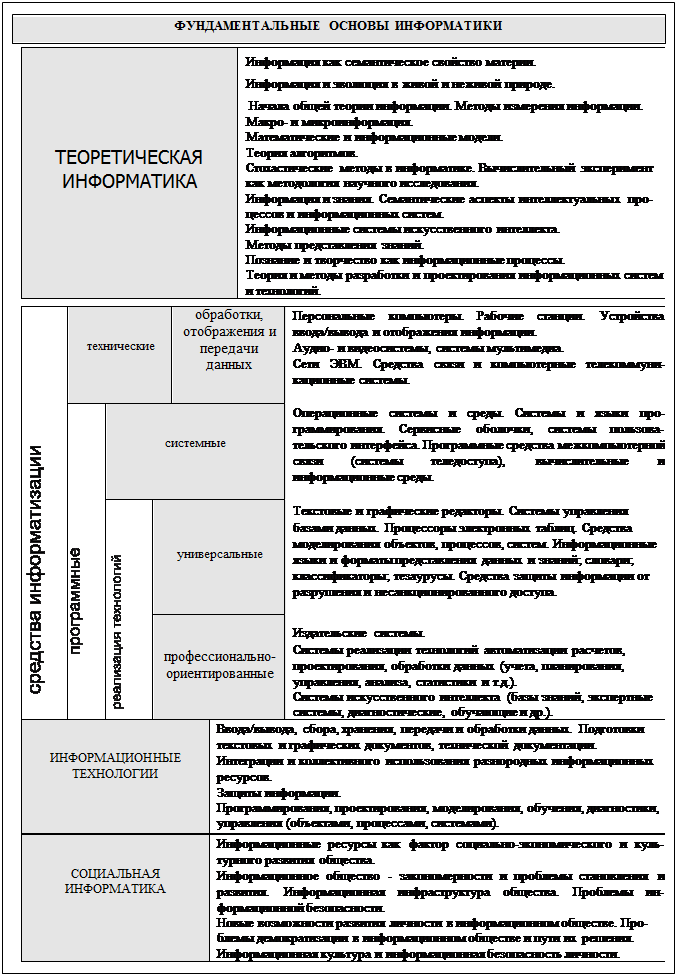
Компьютерная информационная технология включает в себя последовательное выполнение определенных этапов работы с информацией. Подготовительные этапы  выполняются  непосредственно человеком, исполнительные - машиной или машиной с участием человека (диалоговые режимы работы ЭВМ).

На подготовительных этапах осуществляется содержательный и формализованный анализ решаемой задачи,  выбор метода и математической модели ее решения. Определяются последовательность и порядок решения, его алгоритмическое описание, составляются программы на каком-либо доступном для машины языке.  Затем программы вводятся в ЭВМ, отлаживаются, редактируются и записываются для хранения на внешних носителях.

Содержание исполнительных этапов зависит от характера задачи и типа используемой ЭВМ.  Оно сводится к автоматическому выполнению программы, причем часть программы может выполняться с участием человека.  Завершающим этапом является анализ, оценка полученных результатов для их практического использования и  совершенствования разработанных алгоритмов и программ.

Содержание подготовительных этапов  существенно  упрощается, если имеются готовые программы,  соответствующие характеру решаемых задач.  Тогда основная часть работы - операции с данными:  их отбор, ввод в ЭВМ, формирование массивов данных и др. Вызов программы и ее выполнение осуществляются в соответствии с инструкциями по эксплуатации данной ЭВМ.

Характерной чертой современных компьютеров является то,  что преобладающая их часть (по данным специалистов,  до 80 %) используются не для решения вычислительных  задач,  а для разнообразной обработки информации.  Это - обработка текстов, выполнение графических работ,  накопление и оперативная выдача разнообразных данных, программное предъявление информации в процессе компьютерного обучения, автоматизированный контроль знаний и др.

2. Понятие информации

"Нет, пожалуй, в науке, практике современности понятия распространеннее, нежели понятие "информация".  И нет в то же время другого понятия, по поводу которого ведется столько споров,  дискуссий, имеется  столько  различных точек зрения...",- утверждает российский ученый В.Г. Афанасьев.

Накопление человечеством опыта и знаний при освоении природы  смешалось с освоением информации. Информация в  переводе с латинского языка означает: разъяснение, изложение чего-либо или сведения о чём-либо.  Такое понятие, как обработка информации, появилось совсем недавно, но обрабатывать информацию люди начали ещё в древние времена.

Сначала из  поколения  в  поколение информация передавалась устно. Это были сведения о про-фессиональных навыках,  например, о приёмах охоты, обработки охотничьих трофеев,  способах земледелия и др.  Но затем информацию стали фиксировать в виде  графических  образов  окружающего мира. Так, первые наскальные рисунки, изображающие животных, растения, людей,  появились примерно 20-30 тыс. лет назад.

Начатый поиск более современных способов фиксирования информации привёл к появлению письменности. Вначале люди записывали расчёты с покупателями, а затем написали и первое слово.  На чём только они ни писали! В Индии - на пальмовых листьях,  в Вавилоне - на глиняных  плитках, на  Руси пользовались берестой.  Как видим,  письменность – новый шаг человечества в области хранения и передачи информации. Однако первым революционным  явлением  в  этой сфере стало изобретение печатного станка, благодаря которому появилась книга и, таким образом, стало возможно массовое тиражирование профессиональных знаний,  зафиксированных на материальном носителе.

Сегодня потоки книг,  сливаясь с потоками технической документации и многотомной справочной литературы, образуют океаны информации. Эту информацию необходимо хранить и передавать  потребителю, для чего нужен мобильный и ёмкостный носитель.

Но книга является неудобным,  сложным, дорогим, а главное, "медленным" носителем информации.  Вся многогранность содержания раскрывается человеку при перелистывании,  чтении и рассматривании книги. Таким образом, она не может непосредственно влиять  на  производственный  процесс. Сначала человеку необходимо найти нужную ему книгу,  освоить накопленные в ней знания,  которые позже смогут дать толчок  дальнейшему развитию производства. Хранение книг требует громадных зданий и специальных климатических условий,  а их доставка потребителю  сопряжена  с дорогостоящим размножением  во множестве экземпляров и объёмными транспортными перевозками. Книга как носитель информации сегодня уже отстаёт от  стремительного продвижения человечества по пути освоения природы.

Революционное изобретение XX века  -  Электронная  Вычислительная Машина (ЭВМ).  Она-то и является носителем информации и средством доставки её потребителю.  В совокупности с линиями связи ЭВМ делает доступной и мобильной любую часть гигантского объёма информации,  которая без  непосредственного воздействия на человека может влиять на работу производственного оборудования,  например, на станки с программным управлением. На заводах внедряются автоматизированные линии и даже целые автоматизированные производства.

Начала общей теории информации

Информация - это обозначение содержания, полученного от внешнего мира в процессе приспособления к нему (Винер). Информация - отрицание энтропии (Бриллюэн). Информация – коммуникация,  связь, в процессе которой устраняется неопределенность (Шеннон). Информация - передача разнообразия (Эшби). Информация - оригинальность, новизна. Информация - мера сложности структур (Моль). Информация - вероятность выбора (Яглом) и т.д. Каждое из этих определений раскрывает ту или иную грань (аспект) этого многозначного понятия.

Существование множества определений информации  обусловлено сложностью, специфичностью и многообразием подходов к толкованию сущности этого понятия. В качестве справки выделим три  наиболее распространенные концепции информации, каждая из которых по-своему объясняет ее сущность.

Первая концепция (концепция К.Шеннона), отражая количественно-информационный подход, определяет информацию как меру неопределенности (энтропию) события. Количество информации в том или ином случае зависит от вероятности его получения: чем более вероятным является сообщение, тем меньше информации содержится в нем. Этот подход, хоть и не учитывает смысловую сторону информации, оказался весьма  полезным в технике связи и вычислительной технике, послужил основой для измерения информации и оптимального кодирования сообщений. Кроме того, он представляется удобным для иллюстрации такого важного свойства информации, как новизна, неожиданность сообщений. При таком понимании информация - это снятая  неопределенность или результат выбора из набора возможных альтернатив.

Более трех десятилетий существуют два различных подхода, две противостоящие друг другу концепции информации - атрибутивная и функциональная.

"Атрибутисты" квалифицируют информацию как свойство всех материальных объектов, т.е. как атрибут материи. Появление атрибутивной концепции связано с развитием кибернетики и основано на утверждении, что информацию содержат любые сообщения, воспринимаемые  человеком или приборами.  Наиболее ярко и образно эта концепция информации выражена академиком В. М. Глушковым. Он писал, что "информацию несут не только испещренные буквами листы книги или человеческая речь, но и солнечный свет, складки горного хребта, шум водопада, шелест травы". Иными словами, информация  как свойство материи создает представление о ее природе и структуре, упорядоченности, разнообразии и т.д. Она не может существовать вне материи, а значит, она существовала и будет существовать вечно, ее можно накапливать, хранить, перерабатывать.

"Функционалисты", напротив, связывают информацию лишь с функционированием самоорганизую­щихся систем. По их мнению, информация принадлежит лишь управляемым системам (живым и кибернетиче­ским). Они констатируют, что  самоорганизующие системы "возникают исторически в период становления жизни на Земле".  Эта концепция  основана на логико-семантическом (семантика – изучение текста с точки зрения смысла) подходе, при котором информация трактуется как знание, причем не любое знание, а та его часть, которая используется для ориентировки, для активного действия, для управления и самоуправления. Иными словами, информация – это действующая, полезная, "работающая" часть знаний. Представитель этой концепции В.Г. Афанасьев, развивая логико-семантический подход, дает определение социальной информации: "Информация, циркулирующая в обществе, используемая в управлении социальными процессами, является социальной информацией. Она представляет собой знания, сообщения, сведения о социальной форме движения  материи и о всех других формах в той мере,  в какой она используется обществом..."

Итак, рассмотренные подходы в определенной мере дополняют друг друга, освещают различные стороны сущности понятия информации и облегчают тем самым систематизацию ее основных свойств.  Из множества определений информации наиболее целесообразным представляется следующее:

	G

 

Информация – это сведения, снимающие неопределенность об окружающем мире, которые являются объектом хранения, преобразования, передачи и использования. Сведения - это знания, выраженные в сигналах, сообщениях, известиях, уведомлениях и т.д.

 

Особенность информации в том, что, будучи материальным явлением, она не является ни материей, ни энергией. В кибернетическом смысле информация – это отражение одного объекта в другом, используемое для формирования управленческих воздействий. Использование информации в управлении и самоуправлении опирается на наличие связи между объектами системы, источниками информации и ее получателями. При этом сила и целенаправленность влияния информации на  получателя  зависит от степени соответствия характеристик информации (синтаксических, семантических, прагматических)­ возможностям и потребностям получателя. Структура сообщений, их смысл и практическая ценность всегда ориентированны на определенного получателя.

Обмен информацией совершается не вообще  между любыми объектами, а только между теми из них, которые представляют собой систему, обладающую каким-то минимум организованности. В целом возникновение и развитие теории информации, а также кибернетики и информатики явилось научным подтверждением  теории  отражения  и способствовало ее дальнейшему развитию.

3. Формы представления информации, ее виды и  свойства

В своей повседневной деятельности люди широко используют различные виды информационной  техники: радиопередатчики, телевидение,  магнитофоны, телеграфию, вычислительную технику.  Сигналы, передаваемые по радио и телевидению,  а также используемые  в  магнитной  записи,  имеют форму непрерывных, быстро изменяющихся во времени кривых линий.  Такие сигналы называются непрерывными  или  аналоговыми сигналами.  В противоположность этому в телеграфии и вычислительной технике  сигналы  имеют импульсную форму  и  именуются  дискретными сигналами. 

Формы представления информации и ее виды

Исходя из сказанного, можно сделать вывод,  что  информация передается в двух  формах:

·       дискретная форма представления информации – это последовательность символов, характеризующая прерывистую, изменяющуюся величину;

·       аналоговая или непрерывная форма представления  информации – это величина, характеризующая процесс, не имеющий перерывов или промежутков.

Все многообразие окружающей нас информации можно сгруппировать по различным признакам. Информацию разделяют на:

1.     Структурную (или связанную), присущую объектам неживой и живой природы естественного и искусственного происхождения;

2.     Оперативную (или рабочую), циркулирующую между объектами материального мира и используемую в процессах управления в живой природе, в человеческом обществе.

Различают виды информации по способу передачи и восприятия.  Информацию, передаваемую видимыми образами и символами, называют визуальной, звуками – аудиальной, ощущениями – тактильной, запахами и вкусами – органолептической, информацию, выдаваемую и воспринимаемую средствами вычислительной техники, – машинной.

Разнообразие источников и потребителей информации привело к существованию различных форм ее представления: символьной, текстовой и графической.

Символьная форма, основанная на использовании символов – букв, цифр, знаков и т.д., является наиболее простой, но она практически применяется только для передачи несложных сигналов о различных событиях. Примером может служить зеленый свет уличного светофора, который сообщает о начале движения пешеходам или водителям автотранспорта.

Более сложной является текстовая форма представления информации. Здесь так же, как и в предыдущей форме, исполь­зуются символы: буквы, цифры, математические знаки. Однако информация заложена не только в этих символах, но и в их сочетании, порядке следования. Так, слова “КОТ” и “ТОК” имеют одинаковые буквы, но содержат различную информацию. Благодаря взаимосвязи символов и отображению речи человека текстовая информация чрезвычайно удобна и широко ис­пользуется в различной деятельности: (книги, брошюры, журналы, различного рода документы, аудиозаписи и т.д.).

Наиболее емкой и сложной является графическая форма представления информации. К этой форме относятся фотографии, схемы, чертежи, рисунки, играющие большое значение в деятельности человека.

Переходя к рассмотрению свойств информации, необходимо отметить, что информация выступает как свойство объектов и явлений (процессов) порождать многообразие состояний, которые посредством отражения передаются от одного объекта к другому и запечатляются в его структуре (возможно, в измененном виде).

Свойства информации

Свойства информации можно рассматривать в трех аспектах: техническом - это точность, надежность, скорость передачи сигналов и т.д.; семантическом – это передача смысла текста с помощью кодов и  прагматическом – это уровень эффективности влияния информации на поведение объекта.

 Рассмотрим свойства информации, т. е. ее качественные признаки.

1. Объективность информации. Информация — это отражение внешнего мира, а он существует независимо от нашего сознания и желания. Поэтому в качестве свойства информации можно выделить ее объективность. Информация объективна, если она не зависит от чьего-либо мнения, суждения.

• Пример. Сообщение «На улице тепло» несет субъективную информацию, а сообщение «На улице 22⁰С» — объективную (если термометр исправен). Объективную информацию можно получить с помощью исправных датчиков, измерительных приборов. Но, отражаясь в сознании конкретного человека, инфор­мация перестает быть объективной, так как преобразовывается (в большей или меньшей степени) в зависимости от мнения, суждения, опыта, знания или «вреднос­ти» конкретного субъекта.

2. Достоверность информации. Информация достоверна, если она отражает истинное положение дел. Объективная информация всегда достоверна, но достоверная информация может быть как объективной, так и субъективной. Достоверная информация помогает принять нам правильное решение. Недостоверной информация может быть по следующим причинам:

• преднамеренное искажение (дезинформация);

• искажение в результате воздействия помех («испорченный телефон»);

• значение реального факта преуменьшается или преувеличивается (слухи, рыбацкие истории).

3. Полнота информации. Информацию можно назвать полной, если ее доста­точно для понимания и принятия решения.

• Например, мечта историка — иметь полную информацию о минувших эпохах. Но историческая информация никогда не бывает полной, и полнота инфор­мации уменьшается по мере удаленности от нас исторической эпохи. Даже события, происходившие на наших глазах, не полностью документируются, многое забывается, и воспоминания подвергаются искажению.

Неполная информация может привести к ошибочному выводу или решению. Не зря русская пословица гласит: «Недоученный хуже неученого».

4. Актуальность (своевременность) информации — важность, существен­ность для настоящего времени. Только вовремя полученная информация может принести необходимую пользу. Неактуальной информация может быть по двум причинам: она может быть устаревшей (прошлогодняя газета) либо незначимой, ненужной (например, сообщение о том, что в Италии снижены цены на 5%).

5. Полезность или бесполезность (ценность) информации. Так как границы между этими понятиями нет, то следует говорить о степени полезности применительно к нуждам конкретных людей. Полезность информации оценивается по тем задачам, которые мы можем решить с ее помощью.

Самая ценная для нас информация—достаточно полезная, полная, объективная, достоверная и новая. При этом примем во внимание, что небольшой процент бесполезной информации даже помогает, позволяя отдохнуть на неинформативных участках текста. А самая полная, самая достоверная информация не может быть новой.

С точки зрения техники свойство полезности рассматривать бессмысленно, так как задачи машине ставит человек.

4. Кодирование информации

В настоящее время разнообразная по своему значению информация, зафиксированная на специальных носителях, стала национальным богатством нового типа – информационным ресурсом государства. Являясь предметом купли-продажи во все времена, информация имеет свои специфические особенности: при обмене информацией ее  количество увеличивается. "Если у вас есть по яблоку, и вы обменяетесь ими, у вас опять будет по яблоку, но если у вас есть по идее и вы обменяетесь, то у каждого их будет по две".  Общение людей, информирование друг друга приводит к их сближению, повышению интеллектуального потенциала. У информационных ресурсов есть уникальное свойство – они не убывают от интенсивного использования.  Более того, в процессе применения они постоянно развиваются и совершенствуются, избавляясь от ошибок и  уточняя свои параметры.

В определении практической ценности информации нет каких-либо точных количественных парамет­ров. Да и определить их нелегко, поскольку ценность зависит от полезности информации для множества кон­кретных людей, ее получателей и пользователей. Ценность информации принято определять величиной тех потерь, которые эта информация предотвращает, или величиной затрат на добывание этой  информации.

Анализируя информацию, мы сталкиваемся с необходимостью оценки качества  и  определения количества получения информации. Определить качество информации чрезвычайно сложно,  а часто и вообще невозможно. Какие-либо сведения, например исторические, могут десятилетиями считаться ненужными и вдруг их ценность может резко возрасти. Вместе с этим определить количество информации не только нужно, но и можно.  Это, прежде всего, необходимо для того, чтобы сравнить друг с другом массивы информации, определить, какие размеры должны иметь материальные объекты (бумага, магнитная лента и т.д.), хранящие эту информацию.

Для определения количества информации нужно найти способ представить любую ее форму (символьную, текстовую, графическую) в едином виде.  Иначе говоря, надо суметь эти формы информации преобразовать так,  чтобы она получила единый стандартный вид. Таким видом стала так называемая двоичная форма представления информации. Она заключается в записи любой информации в виде последовательности только двух символов.

Эти символы могут на бумаге обозначаться любым способом: буквами А, Б; словами ДА, НЕТ. Однако ради простоты записи взяты цифры 1 и 0. В электронном аппарате, хранящем, либо обрабатывающем информацию, рассматриваемые символы могут также обозначаться  по-разному: один  из них - наличием в рассматриваемой точке электрического тока, либо магнитного поля,  второй - отсутствием  в  этой точке электрического тока, либо магнитного поля.

Методику представления информации в двоичной форме можно пояснить, проведя следующую игру.  Нужно у собеседника получить интересующую нас информацию,  задавая любые вопросы,  но получая  в ответ только одно из двух: ДА либо НЕТ. Известным способом получения во время этого диалога двоичной формы информации является перечисление всех возможных событий. Рассмотрим простейший случай получения информации. Вы задаете только один вопрос: "Идет ли дождь?". При этом условимся, что с одинаковой вероятностью ожидаете ответ: "ДА" или "НЕТ". Легко увидеть, что любой из этих ответов несет самую малую порцию информации. Эта порция определяет единицу измерения информации, называемую БИТОМ. Благодаря введению понятия единицы информации появилась возможность определения размера любой информации числом битов. Образно говоря, если, например, объем грунта определяют в кубометрах, то объем информации - в битах. Условимся каждый  положительный ответ представлять цифрой 1, а отрицательный - цифрой 0.  Тогда запись всех  ответов  образует многозначную последовательность  цифр,  состоящую из нулей и единиц, например 0100.

Рассмотренный процесс получения двоичной информации об объектах исследования называют кодированием информации.

Кодирование информации перечислением всех возможных событий очень трудоемко. Поэтому на практике кодирование осуществляется более простым способом. Он основан на том, что один разряд последовательности двоичных цифр имеет уже вдвое больше различных значений - 00,  01, 10, 11, - чем одноразрядная (0 и 1). Трехразрядная  последовательность  имеет также вдвое больше значений - 000, 001,  010,  011,  100, 101, 110, 111, - чем двухразрядная, и т.д. Добавление одного разряда увеличивает число значений вдвое,  это позволяет составить следующую таблицу информационной емкости  чисел:

Таблица 1 Информационная емкость чисел

Количество двоичных разрядов
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16384	32768	65536
Количество двоичных значений

 

Пользуясь вышеприведенной таблицей, легко закодировать любое множество событий.  Например, нам нужно закодировать  32 буквы русского алфавита,  для этой цели достаточно взять пять разрядов, потому что  пятиразрядная  последовательность  имеет 32 различных значения. В информационных  документах  широко  используются не только русские, но и латинские буквы, цифры, математические знаки и другие специальные  знаки  всего примерно 200-250 символов.  Поэтому для кодировки всех указанных символов используется  восьмиразрядная последовательность цифр 0 и 1. Например, русские буквы представляются восьмиразрядными  последовательностями следующим образом: А - 11000001,  И - 11001011, Я - 11011101.

На ЭВМ данные представляются битами. Бит может иметь одно из двух значений - 0 или 1.  Принято информационную единицу, образуемую последовательностью из 8 бит,  называть байтом (1 байт = 8 бит). Последовательность бит образует число в двоичной системе исчисления. В нашем случае в одном байте мы можем хранить максимальное число, равное 11111111, что при переводе в десятичную систему исчисления обозначает 255.

Но почему в байте содержится именно 8 бит? С появлением ЭВМ возник вопрос: "Сколько бит должна содержать информационная единица?". После некоторых размышлений сошлись на том, что 256 чисел вполне хватит для адресации команд и кодировки символов.

Кроме этих двух единиц измерения существуют и другие, например килобайт (1024 байт), мегабайт (1024 килобайт), гигабайт (1024 мегабайт) и т.д.

5. Системы счисления

Система счисления – принятый способ записи и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса: позиционные и непозиционные. Для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Из непозиционных систем счисления до наших дней дошла и часто используется римская система счисления, в которой используется свой набор знаков I, V, X, L, C, D, M и определенные правила формирования чисел, которые очень просты и мы не будем их рассматривать, просто приведем последовательность из десяти римских чисел: I, II, III, IV, V, VI, VII, VIII, IX, X, …   Выводы сделайте сами.

Разберем более подробно позиционные системы счисления. Число знаков в позиционной системе счисления, используемых для формирования чисел, называется основанием системы счисления. Ниже приведена таблица, содержащая наименования некоторых позиционных систем счисления и перечень знаков (цифр), из которых образуются в них числа.

Таблица 2. Некоторые системы счисления

 

Следует заметить, что систем счисления существует бесконечное множество с любым количеством знаков большим единицы, по этому кроме этих систем вам могут встретиться и системы с основанием 7, 24, 32, 60, 100, 365 и т.д. Кстати, шестидесятеричной системой счисления мы пользуемся ежедневно – время мы отсчитываем в секундах, минутах и часах. В одной минуте 60 секунд, в одном часе 60 минут.  

Совокупность различных цифр, используемых в позиционной системе счисления для записи чисел, называется алфавитом системы счисления.

При рассмотрении позиционных систем чрезвычайно важным является понятие базиса системы счисления.

Базис позиционной системы счисления – это последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.

Выпишем базисы некоторых традиционных систем счисления.

Десятичная система: 1, 10, 10², 10³, 10⁴, …,10ⁿ, … .

Двоичная система: 1, 2, 2², 2³, 2⁴, …,2ⁿ, … .

Восьмеричная система: 1, 8, 8², 8³, 8⁴, …,8ⁿ, … .

В позиционной системе счисления число может быть представлено в виде суммы произведений коэффициентов на степени основания системы счисления (в виде многочлена):

A_p…A₁A₀ , A_–1…A_{q–1 =} A_p*B^p + … +A₀*B⁰ + … +A_q–1*B^q–1

Представление числа в B–ичной системе счисления в виде A_p…A₁A₀ , A_–1…A_q–1  называется свернутой формой записи числа (эта форма наиболее употребима при изображении чисел в позиционных системах счисления).

Представление числа в B–ичной системе счисления в виде A_p*B^p + … +A₀*B⁰ + … +A_q–1*B^q–1  называется развернутой формой записи числа (эта форма в основном используется при решении задач).

Значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Именно поэтому такие системы называют позиционными.

Примеры записи чисел

23,43₁₀ = 2*10¹ + 3*10⁰ + 4*10^–1 + 3*10^–2  (в данном примере знак «3» в одном случае означает число единиц, а в другом – число сотых долей единицы);

692₁₀ = 6*10² + 9*10¹ + 2*10⁰  («шестьсот девяносто два» с формальной точки зрения представляется в виде «шесть умножить на десять в степени два, плюс девять умножить на десять в степени один, плюс два»);

1011₂ = 1*2³ + 0*2² + 1*2¹ + 1*2⁰;

413,2₈ = 4*8² + 1*8¹ + 3*8⁰ + 2*8^–1;

B2F,7₁₆ = B*16² + 2*16¹ + F*16⁰ + 7*16^–1;

При работе с компьютерами приходится параллельно использовать несколько позиционных систем счисления (чаще всего двоичную, десятичную и шестнадцатеричную), поэтому большое практическое значение имеют процедуры перевода чисел из одной системы счисления в другую. Заметим, что во всех приведенных выше примерах результат является десятичным числом, и, таким образом, способ перевода чисел из любой позиционной системы счисления в десятичную уже продемонстрирован.

Таблица 3. Соответствие чисел в различных системах счисления

 

Преобразование чисел из произвольной системы счисления в десятичную

Для преобразования числа из произвольной системы счисления в десятичную достаточно представить это число в виде многочлена со степенями основания и найти значение этого многочлена.

Простая задача. Преобразовать число 110101,01₂ из двоичной записи в десятичную.

Решение. Представим число в виде многочлена и найдем его значение:

110101,01₂ = 1 * 2^б + 1 * 2⁴ + 0 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰ + 0 * 2^–1 + 1 * 2^–2 = 53,25₁₀

Поэтому значение многочлена равно числу 53,25 (конечно, в десятичной записи).

Преобразование чисел из десятичной системы счисления в произвольную

Преобразовать число из десятичной системы счисления в любую другую немного сложнее. Для этого можно разбить число на две части: целую и дробную. Чтобы перевести целую часть числа из десятичной системы в систему с основанием В, необходимо ее разделить на В. Остаток даст младший разряд числа. Полученное при этом частное необходимо вновь разделить на В – остаток даст следующий разряд числа и т.д. Для перевода дробной части ее необходимо умножить на В. Целая часть полученного числа будет первым (после запятой, отделяющей целую часть от дробной) знаком. Дробную же часть произведения необходимо вновь умножить на В. Целая часть полученного числа будет следующим знаком и т.д. Заметим, что конечная десятичная дробь при этом вполне может стать бесконечной (периодической).

Пример 1. Преобразовать число 25,73 из десятичной записи в двоичную.

Решение. Разобьем число на целую и дробную части и переведем каждую из частей по описанным выше правилам:

Таблица 4.

Таким образом,   25,73₁₀ = 1101,10111₂. 

Пример 2. Преобразовать число 58,32 из десятичной записи в восьмеричную.

Решение. Разобьем число на целую и дробную части и выполним действия аналогичные предыдущему решению.

Таблица 5..

Перевод целой части числа		Перевод дробной части числа
	Остаток		Целая часть
53 : 8  = 7                                                      7 : 8 = 0	(2), (7).	0,32 * 8 = 2,56 0,56 * 8 = 4,48 0,48 * 2 = 3,84 …	(2), (4), (3).

Таким образом,   53,32₁₀ = 72,243₈.

Для перевода целого двоичного числа в восьмеричное необходимо разбить его справа налево на группы по 3 цифры (самая левая группа может содержать менее трех двоичных цифр), а затем каждой группе поставить в соответствие ее восьмеричный эквивалент. Например, дано число 11011001₂. Разбиваем его на триады  11011001₂ = 11 011 001. Из таблицы соответствия чисел в различных системах счисления находим   11₂ = 3₈,  011₂=3₈,   001₂=1₈,  откуда следует,  что   11011001₂ = 331₈.

Перевод целого двоичного числа в шестнадцатеричное производится путем разбиения данного числа на группы по 4 цифры – двоичные тетрады. Например, 1100011011001₂ = 1 1000 1101 1001 => 18В9₁₆.

Перевод восьмеричных (шестнадцатеричных) чисел в двоичные производится обратным путем – сопоставлению каждому знаку числа соответствующей тройки (четверки) двоичных чисел.

Преобразования чисел из двоичной в восьмеричную и шестнадцатеричную системы и наоборот столь просты (по сравнению с операциями между этими тремя системами и привычной нам десятичной) потому, что числа 8 и 16 являются целыми степенями числа 2. Этой простотой и объясняется популярность восьмеричной и шестнадцатеричной систем в вычислительной технике и программировании.

6. Двоичная арифметика

Для того, чтобы производить арифметические действия над двоичными числами, надо знать таблицу сложения и умножения в двоичной системе.

Приведем таблицы сложения и умножения в двоичной системе счисления:

Таблица 6.

 

Сложение двоичных чисел

Таблица сложения в двоичной системе счисления предельна проста. Так как 1+1 = 10₂, то при сложении столбиком в данном разряде остается 0, а 1 переносится в следующий разряд.

Рассмотрим несколько примеров выполнения операции сложения в двоичной системе.

Таблица 7.

               

Из приведенного примера видно, что при сложении столбиком двух цифр справа налево в двоичной системе, как и в любой позиционной системе счисления, в следующий разряд может переходить только единица.

Вычитание двоичных чисел

При выполнении операций вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак.

Пример. Вычислить: 11₂ – 1011₂ .

Так как уменьшаемое меньше, чем вычитаемое, то следует вычесть 11₂ из 1011₂, приписав к результату знак «–»:  11₂ – 1011₂  = – (1011₂ – 11₂) = –1000₂.

Рассмотрим несколько примеров вычитания чисел столбиком:

Таблица 8.

 

При «заеме» из более старшего разряда в текущий разряд приходит две единицы, так как единица более старшего разряда равна основанию системы, то есть двум.

Умножение двоичных чисел

Операция умножения в двоичной системе выполняется с использование таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.

Рассмотрим несколько примеров умножения чисел столбиком:

Таблица 9.

 

Из приведенных примеров видно, что в двоичной системе операция умножения сводится к сдвигам множимого и сложению промежуточных результатов.

Деление двоичных чисел

Операция деления в двоичной системе выполняется по правилам, подобным правилам выполнения деления в десятичной системе счисления.

При делении столбиком приходится в качестве промежуточных вычислений выполнять действия умножения и вычитания. Но в двоичной системе промежуточные умножения сводятся к умножению делителя или на 0 или на 1, поэтому наиболее сложной остается лишь операция вычитания, которую надо научиться делать безошибочно.

Рассмотрим несколько примеров деления целых чисел:

Таблица 10.

 

Если в результате выполнения операции деления не получается конечная дробь, то выполнять операцию деления можно до выделения периода или до получения требуемого количества знаков после запятой. Для второго примера ответ можно записать как 10,(10).

Операции над числами в восьмеричной (шестнадцатеричной) системе счисления выполняются по аналогичным правилам, и рассматриваться нами в этом разделе не будут. Постарайтесь самостоятельно разобраться с этим вопросом.

 

7. ЭВМ и двоичная система счисления

G

Базовым элементом в ЭВМ является триггер.

 

Триггер – это электрический элемент, который может находиться в двух устойчивых состояниях: включено или выключено, аналогично выключателю.

 

ЭВМ построена на двоичной системе счисления, каждому из состояний триггера мы можем сопоставить 0 или 1. В обоих состояниях триггер стабилен, что придает хранящейся в нем двоичной информации очень высокую надежность. Существуют и другие преимущества двоичной системы счисления. Передача информации в компьютере осуществляется посредством передачи электрических импульсов. Характеристиками электрического сигнала являются сила тока и напряжение. На электрические сигналы большое влияние оказывают помехи, создаваемые внешними электромагнитными полями. Вспомните, как ухудшается радиоприем или качество  телевизионного изображения  в дождливый день. Электрические сигналы в компьютере также подвержены помехам и существенность этих помех гораздо больше, чем при радио или телепередаче, где из-за мельтешения полос на экране мы все же можем разглядеть лицо любимого актера... Как же эта проблема решается в компьютере? За счет двоичной системы счисления!

Как с помощью электрической волны передать информацию? Рассмотрим два решения: при помощи десятичной системы счисления и двоичной. Каждой цифре десятичной системы счисления сопоставим величину напряжения:

 

Таблица 11.

 

Аналогично для двоичной системы, но положим, что U_В £ k_ВОЛЬТ - ноль, а U_В ³ k_ВОЛЬТ - единица. Посмотрим, как будет выглядеть число 10110100₂ = 180₁₀ в виде волны.

 

двоичная                                                                      десятичная

 

 

 

Добавим шумовую волну такого вида:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

               

 

 

 

 

 

При сложении получаем волны следующих форм:

 

 

Рис. 1

 

Если «определить» следующую ступень в волне, которая представляет число в десятичной системе счисления, то получим приблизительно 371, т.е. информация потеряна! Проделаем те же действия с волной, которая представляет нам число в двоичной системе, и мы получим исходное - 10110100₂, так как шумовая волна для нас окажется несущественной. Вследствие устойчивости двоичного сигнала к помехам и того, что производить элементы с двумя устойчивыми состояниями  легче, современные компьютеры обрабатывают информацию в двоичной системе.

               

8. Азбука машинной логики. Логические операции, элементы и функции

То, что компьютер работает на основе двоичной системы счисления, это вам уже известно, но как и с помощью каких устройств обрабатываются двоичные сигналы?

Устройство ЭВМ пред­ставляет собой комбинации большого числа элементов-кирпичиков. Разнообразие их, однако, не столь велико. Каждая машина состоит из ограниченного количества типов элементов, которые выполняют определенные ло­гические функции, выражающие зависимость двоичных сигналов на выходах от двоичных сигналов на входах этих элементов.

Логические операции

Построение и анализ логических элементов и схем ЭВМ основываются на применении формального метода математики к области логики. Подобно тому, как в математике для выражения отношений используется язык формул, в математической логике тот же язык формул используется для выраже­ния логических связей, которые существуют между суж­дениями, понятиями, высказываниями. Так же, как и для математической задачи, решение любой логической задачи имеет свою «технологию». Она составляется из простейших операций, похожих на сло­жение и умножение.

Основоположником математической логики считают великого немецкого математика Лейбница. Это он в XVII веке попытался построить первые логические исчисле­ния. Он сблизил логику с исчислением, усовершенство­вал и уточнил логическую символику.

На фундаменте, заложенном Лейбницем, другой вели­кий математик Джордж Буль (отец писательницы Э. Войнович, автора романа «Овод»)   воздвиг здание новой области науки — математической логики. Он вывел для логических построений особую алгебру — алгебру ло­гики. В ней, в отличие от обычной алгебры, символами обозначают не числа, а высказывания.

Высказыванием может быть любое замечание, сооб­щение или утверждение об объективно существующем мире. Высказывание может совпадать или не совпадать с действительностью, в которой оно что-то утверждает. В первом случае мы называем высказывание истинным, во втором — ложным. Таким образом, уже по самой своей сути высказывания являются двоичными функ­циями.

Принято считать, что значение истинности высказы­вания равно единице, если оно истинно, и равно нулю, если оно ложно. Например, высказывания «земля вра­щается», «мел белый» — истинны, и значения их истинно­сти равны 1. А вот высказывания «земля не вращается», «мел не белый» — ложны, и значения их истинности равны 0.

Если условно обозначить различные высказывания буквами А, В и т.д., то в общем виде запись А = 1 означает, что высказывание А истинно, а В=0 означает, что высказывание В ложно.

То, что значение истинности может принимать два значения — 0 и 1, хорошо согласуется с двоичной сис­темой счисления и с работой двухпозиционных элемен­тов, используемых в ЭВМ.

Например, в ЭВМ истинность высказывания может быть передана сигналом положительного электрического напряжения, что условно соответствует сигналу 1, а лож­ность — сигналом отрицательного напряжения или отсут­ствием вообще какого-либо сигнала. Это условно соот­ветствует сигналу 0.

Высказывания могут быть простыми и сложными. Из данных высказываний с помощью логических опера­ций можно получить новые высказывания. Простейшая операция — отрицание некоторого высказывания. Если дано высказывание А, то его отрицание НЕ обозначают той же буквой, но с черточкой наверху, что читается как «не А». Эта логическая операция называется инверсией. Например: «идет дождь» — А, «не идет дождь» — А.

Инверсию (отрицание) и другие логические опера­ции можно пояснить с помощью диаграммы, предложенной английским логи­ком Венном. Пусть круг на рисунке 1.2, а обозначает высказывание А, тогда отрицанию этого высказывания соответствует остальная площадь четырехугольника, т. е. все то, что не относится к А.

Если теперь высказывание А истинно, то А=1, а  А=0, так как в данном случае высказывание, напри­мер, «дождь не идет»,  было бы ложным. И наоборот, если А — ложно, то  А = 1. Это правило является в логике общим и отображается таблицей истинности.

Таблица, изображенная на рисунке 1.2, а, является, таким образом, таблицей истинности операции отри­цания.

Возьмем теперь в качестве высказывания А утвержде­ние «пасмурно», а в качестве высказывания В — утвер­ждение «идет дождь». Если даны два высказывания А и В, то можно определить высказывание «А и В», которое записывается в виде А/\B. Эта логическая операция называется конъюнкцией или логическим И. Читается: «пасмурно и идет дождь». Посмотрите на рисунок 1.2, б. Площадь, принадлежащая обоим кругам, должна соот­ветствовать высказыванию A/\B. Общая для обоих кругов площадь охватывает все то, что относится одновременно и к А, и к В.

Высказывание А/\В («пасмурно и идет дождь») может быть истинным лишь тогда, когда истинны оба входящие в него высказывания. Если хотя бы одно из них ложно, то и результат будет ложным. Это иллюстрирует на ри­сунке 1.2 таблица истинности этой операции (табл. б). Обратите внимание! Эта таблица представляет собой не что иное, как таблицу умножения двух чисел: 1 и 0. По этой причине конъюнкцию часто называют также логи­ческим умножением. Запись F=А·В является вы­ражением логического умножения двух переменных и читается так: F есть А и В. Операция логического умножения (операция И) обозначается также точкой или знаком, который соответствует союзу «и».

Рис. 2 Основные логические функции и элементы

 

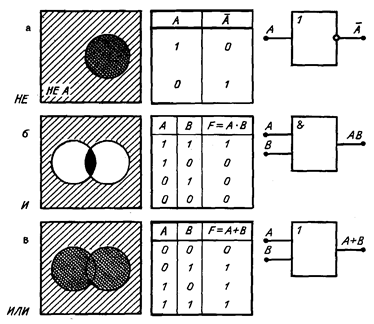Два высказывания А и В могут быть связаны словом ИЛИ. В результате получается новое высказывание «А или В», которое записывается в виде А\/В. Эта операция носит название дизъюнкции. Если в качестве А и В снова взять высказывания «пасмурно» и «идет дождь», то для А\/В получим высказывание «пасмурно или идет дождь». Значение этого ИЛИ поясняет рисунок 1.2, в. Здесь опять оба круга представляют собой высказыва­ние «А и В». Тогда новое высказывание «А или В» изображается площадью, объединяющей оба круга. За­метьте, логическое ИЛИ, выражаемое знаками \/ или +, это не взаимоисключающее «или-или», употребляемое в обычной речи. Заштрихованная область на диаграмме (рис. 1.2, в) содержит все то, что принадлежит А и В, причем «и» следует понимать здесь в смысле объедине­ния или суммирования. Высказывание А\/В ложно лишь тогда, когда ложны оба входящих в него высказывания. Смысл этой форму­лы легко понять, рассмотрев таблицу истинности этой логической операции (табл. в на рис. 1.2). В ее соотноше­ниях находит выражение особенность сложения чисел 1 и 0. Поэтому дизъюнкцию называют иногда также логи­ческим сложением или логической суммой. Запись F =А+В является, таким образом, выражением логиче­ского сложения и читается так: F есть А или В.

Итак, мы познакомились с тремя основными логичес­кими операциями НЕ, И, ИЛИ.

G

 

Схемы, реализующие операции НЕ, И, ИЛИ называют основными или базовыми логиче­скими элементами.

 

Они-то и помогают машине «рассуж­дать» во время работы: И — соединять, ИЛИ — выби­рать, НЕ — отрицать.

Логические элементы

G   Логической функцией (функцией алгебры логики)  называется функция F(x1, x2,…, xn), аргументами которой являются двоичные значения x1, x2, …, xn. Результат  функции есть  двоичное число.

 

Любые сложные логические функции, необходимые для работы машины, могут быть выполнены с помощью основных логических элементов. Сами элементы строятся из разнообразных электриче­ских схем. При этом аргументами являются сигналы, поступившие на вход схемы, а функциями от этих аргу­ментов — выходные сигналы. Если сигнал есть, то значе­ние аргумента, который он изображает, равно единице, если нет — нулю. Поскольку логический элемент машины реализует конкретную логическую функцию, то строго определенной комбинации входных сигналов, отвечаю­щей значениям аргумента, должно соответствовать на­личие (или отсутствие) сигнала на выходе схемы.

Познакомимся теперь с основными логическими эле­ментами и посмотрим, по какому принципу строятся схе­мы, реализующие различные логические операции. На­иболее простыми и распространенными из них являются: схема совпадения, собирательная схема и инвертор.

Схема совпадения (элемент И / AND)

Пусть, например, поставлена задача построить схему, реализующую ло­гическое произведение А·В. Такая схема будет иметь два входа А и В и один выход F=А·В (рис. 1.3). Вход­ные сигналы и результирующий выходной сигнал должны представлять собой электрические импульсы. При этом наличие импульса пусть соответствует 1, отсутствие — 0. Тогда схема электрических соединений должна быть та­кова, чтобы таблица истинности этой логической опера­ции реализовалась в форме импульсов.

С помощью этих символов можно легко представить себе действие элемента И, как показано на рисунке 1.3, а. Такое поведение схемы действительно отражает таб­лицу истинности для логического произведения: 1 на вы­ходе элемента появляется только в том случае, если на обоих входах присутствует 1.

Рис. 3. Логический элемент «И»

Представьте себе электрическую схему, например, цепь из источника тока, лампочки и двух выключателей (на рис. 1.3, 6 они показаны в виде кнопок). Условимся, что цифра 1 обозначает воздействие (кнопка нажата) или результат (лампочка горит). Цифра 0 обозначает отсутствие воздействия (кнопка не нажата) или отсутст­вие результата (лампочка не горит).

 

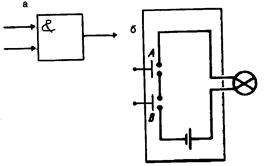Из схемы видно, что лампочка загорится лишь когда будут прижаты к контактам перемычка А и перемычка В. Иными словами, чтобы в нашей цепи прошел сигнал, надо нажать на обе кнопки, включить и первый, и второй вы­ключатели. Подобная схема называется схемой совпаде­ния; в ней только при совпадении во времени обоих сиг­налов на выходе появляется импульс.

Собирательная схема (элемент ИЛИ / OR)

Эта схема ме­нее «привередлива» к характеру входной информации: значение 1 появляется на ее выходе каждый раз, когда хотя бы на одном входе появится значение 1. Действи­тельно, чтобы на схеме, показанной на рисунке 1.4,а, за­горелась лампочка, надо замкнуть цепь хотя бы одной из контактных перемычек: включить первый или второй выключатели. Здесь, в отличие от схемы совпадения, сиг­нал, поступивший на любой из входов, проходит на вы­ход. Поэтому схемы, реализующие логическую операцию сложения, получили название собирательных. Такая схе­ма позволяет в одну точку подать напряжение от раз­личных линий без замыкания их между собой.

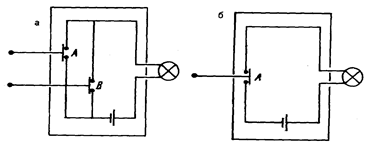Рис. 4.  Логические элементы «ИЛИ» и «НЕ»

 

Схема инвертора (элемент НЕ / NOT)

Схему инвертора, или логическую схему НЕ, можно назвать «цепью наобо­рот». В ней один вход и один выход (рис. 1.4, б). Но им­пульс тока появляется лишь тогда, когда на входе нет сигнала. Действительно, когда кнопку А на­жимают, контактная перемычка отходит от контактов, электрическая цепь размыкается и лампочка гаснет. Когда же кнопка не нажата — сигнала на входе нет — лампочка горит. Следовательно, лампочка ведет себя на­оборот по отношению к кнопке, она отрицательно ре­агирует на ее воздействия.

Комбинации логических элементов

С помощью элементов НЕ, И, ИЛИ можно реализовать любые логиче­ские функции, какими бы сложными они ни были. Может лишь потребоваться для их реализации большее или меньшее количество элементов каждого из этих типов. Все зависит от степени их сложности.

Создатели вычислительных машин, конечно, стремят­ся к тому, чтобы число логических элементов было как можно меньше. Иначе говоря, пытаются подобрать такие электронные схемы, которые позволили бы реализовать необходимые логические функции и вместе с тем содер­жали минимальное число звеньев. Это требование равно­сильно поискам минимального числа схем. При более де­тальном рассмотрении приведенных логических функций оказывается, что для реализации любых логических опе­раций достаточно иметь даже не три, а два логических элемента.

 

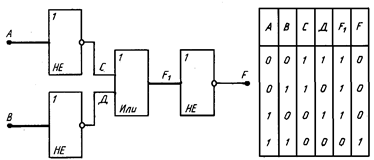Рис. 5.  Построение элемента «И» из элементов «НЕ» и элемента «ИЛИ»

 

Действительно, функция ИЛИ может быть реализо­вана с помощью элементов НЕ и И, а комбинации элементов НЕ и ИЛИ позволяют получить функцию И. Та­кое преобразование функции ИЛИ в функцию И с по­мощью инверсии показано на рисунке 1.5. Сравните на этом рисунке входные и выходные колонки таблицы ис­тинности приведенной логической схемы с таблицей истинности функции И. Они совпадают. Вот и получа­ется, что элементарными логическими функциями можно считать функцию НЕ и одну из функций И или ИЛИ.

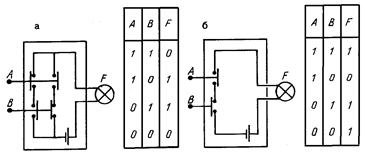Рис. 6. Логические элементы XOR и IMP

 

Соответствующие сочетания простейших элементов позволяют создавать более сложные типовые элементы. На рисунке 1.6, а, б изображены, например, логические элементы, выполняющие функции, обозначаемые соответ­ственно как F=А XOR В и Е=А IMP В. Что представляет со­бой каждая из этих функций, ясно из рассмотрения таб­лиц, приведенных со схемами элементов. Первую из них называют функцией неравнозначности, а по-другому— сумма по модулю два. Вторая функция называется импликацией.

Существуют еще два логических элемента, особен­ностью которых является следующее. Используя их, мож­но строить любые логические устройства, пусть даже содержащие сравнительно большое общее количество элементов. Это элемент НЕ — И, выполняющий функцию, называемую «штрих Шеффера», которая обозначается F=А/В и определяется следующим образом: при комби­нациях значений А и В, указанных в таблицах истин­ности (т.е. при сочетаниях 00, 01, 10, 11), значения F соответственно равны 1, 1, 1, 0. Есть и другой такого же рода логический элемент. Это элемент НЕ — ИЛИ, вы­полняющий функцию, которую называют «стрелка Пир­са», обозначаемую F=А↓В и определяемую так: при указанных выше сочетаниях значений А и В функция F принимает соответственно значения 1, 0, 0, 0.

Легко показать, что каждый из этих элементов явля­ется функционально полным, т. е. при помощи каждого из них могут быть получены любые основные логические элементы, а следовательно построены любые сложные логические схемы. В качестве примера рассмотрим по­строение элемента ИЛИ из элементов И-НЕ  (рис. 1.7). Обозначив выходы первых двух элементов через F1 и F2, получаем:

 

F1= A/\1;    F2 = В/\1;   F=F1/\F2 =A/\B=A\/B.

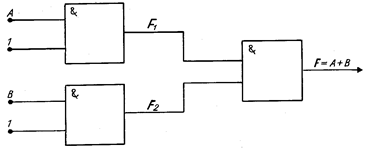Рис. 7.  Построение элемента «ИЛИ» из элементов «И-НЕ»

 

Приведем таблицу истинности для основных логических операций. 

 

Таблица  12.  Таблица истинности логических операций

 

A	B	NOT A	A AND B	A OR B	A XOR B	A EQV B	A IMP B
0 0 1 1	0 1 0 1	1 1 0 0	0 0 0 1	0 1 1 1	0 1 1 0	1 0 0 1	1 1 0 1

 

 

9. Булевы выражения и законы алгебры логики

Так как для алгебры логики значение имеет только результат высказывания – его истинность или ложность, то для компактной записи логических задач используют имена переменных, означающих логическое высказывание и  знаки операций их связывающие.

Задача. Определите, при каких значениях x, y, z  значение выражения (x Ù y) Ù z равно 1? Переменные x, y и z означают логические высказывания, значение которых будем означать так:
«ложь» = 0; «истина» = 1.

Решение. Задача решается составлением следующей таблицы истинности:

Таблица  13.

Ответом будет только одна последняя строка таблицы, т.е. выражение будет равно 1 при x=1, y=1 и z=1.

Задача может быть поставлена и наоборот, когда по имеющейся таблице истинности требуется записать логическое выражение ей соответствующее.

 По имеющейся таблице истинности можно получить булево выражение, используя следующие правила:

1. Для каждой строки таблицы истинности с единичным значением функции построить минтерм. (Минтермом называется терм–произведение, в котором каждая переменная встречается только один раз – либо с отрицанием, либо без него). Переменные, имеющие нулевые значения в строке, входят в минтерм с отрицанием, а переменные со значением 1 – без отрицания.

2. Объединить все минтермы операцией дизъюнкция, что даст стандартную сумму произведений для заданной таблицы истинности.

Задача. Дана таблица истинности:

Таблица  14.

Решение. Построим булево выражение для  F.

Найдем строки, в которых F=1. Это вторая, третья и шестая.

Для второй строки x=0, y=0, z=1. Эту строку описывает минтерм .

Для третей строки x=0, y=1, z=0. Эту строку описывает минтерм .

Для шестой строки x=1, y=0, z=1. Эту строку описывает минтерм .

Объединяя термы, получим булево выражение для F:

F(x,y,z) = Ú Ú

В это выражение вошли термы–произведения для строк с единичным значением функции F, а вся сумма соответствует совокупности из трех строк. Для остальных пяти наборов значений входных переменных это выражение равно нулю. Таким образом, мы построили булево выражение по таблице истинности. В данном случае оно называется стандартной суммой произведений (канонической суммой минтермов).

Полученное таким образом выражение, как правило, можно упростить, применяя законы алгебры логики.

Таблица  15. Законы алгебры логики

 

Законы приведены без доказательств и при желании можете, используя таблицы истинности, доказать равенство левой и правой части для каждого выражения.

Рассмотрим несколько примеров упрощения логических выражений (в скобках укажем номера законов, которые применялись для упрощения выражений. Следует учитывать, что упрощение может быть выполнено и другим способом, так как оно является творческим, а не алгоритмическим процессом).

1. Упростить выражение: F = .

Решение. F = {12} = = {5} =  = {2} = .

2. Упростить выражение: F = .

Решение. F = {4} =  =

= {7} =  =

= {12} =  = {5} =   =

= {7 и 2} =  = {9} = .

 

Контрольные вопросы

1.         Что такое информатика?

2.         Что такое информация?

3.         В чем измеряется информация?

4.         Какие основные источники информации вам известны?

5.         Какие способы передачи информации от человека к человеку вы знаете?

6.         Какие функции выполняют различные органы человека при обработке информации?

7.         Какие основные функции выполняет информация в со­временном обществе?

8.         Корреспондент телевидения, находясь на улице западного города, рассказывает с экрана о каком-то событии. Полу­чаете ли вы при этом дополнительную информацию, кро­ме слов репортера? Если да, то какую и почему?

9.         Какие носители информации Вы знаете?

10.     Приведите примеры информационных процессов в живом организме, в животном мире, в человеческом обществе, в технике.

11.     Приведите примеры, когда компьютер не может заменить человека в деле обработки информации.

12.     Сколько байтов в 10 килобайтах?

13.     Какое максимальное число может быть записано с помощью 2 байтов?

14.     Посчитайте, сколько байт содержит одна страница вашего учебника. Выразите полученное число в килобайтах.

15.     "Сколько битное" кодирование вы бы предложили для языка племени ZzzZz, в алфавите которого целых 16 букв и все большие, а цифр и знаков препинания и вовсе нет?

16.     Если в предыдущем задании ваш ответ -- 4, то найдите ошибку. Без какого символа нельзя обойтись?

17.     Сколько символов можно закодировать, используя UNICODE?

18.     Что такое логическая функция? Что такое таблица истинности?

19.     Назовите основные базовые логические элементы.

Скачано с www.znanio.ru