Лекция 1.

 

Представление данных. Системы счисления

 

Наиболее распространенные - числовые данные могут быть представлены в различном виде. Вид этот определяется используемой системой счисления.

Система счисления (СС) – совокупность приемов и правил представления чисел в виде конечного числа символов. СС имеет свой алфавит (упорядоченный набор цифр и букв) и совокупность операций образования чисел из этих символов.

Системы счисления разделяют на не позиционные и позиционные.

Не позиционная система счисления – это система, в которой цифры не меняют своего количественного эквивалента в зависимости от местоположения (позиции) в записи числа. К не позиционным системам счисления относится, например, система римских цифр, основанная на употреблении латинских букв:

I – 1;

V – 5;

X – 10;

L – 50;

C – 100;

D – 500;

M – 1000.

 

Значение числа в этой системе определяется как сумма или разность цифр в числе (если меньшая цифра стоит перед большей, то она вычитается, а если после - прибавляется). Например, число 1998 записывается как MCMXCVIII.

Не позиционные системы счисления обладают следующими недостатками:

-  сложность представления больших чисел (больше 10000);

-  сложность выполнения арифметических операций над числами, записанными с помощью этих систем счисления.

Позиционная система счисления – это система, в которой количественный эквивалент цифры зависит от ее положения в числе (чем «левее» цифра в записи числа, тем её значение больше). Основание позиционной системы счисления – это количество разных символов в ее алфавите. Например, в двоичной системе счисления используется две цифры (0 и 1), в восьмеричной – восемь (0,1,…,6,7), а в десятичной системе счисления используется десять цифр (0,1,…,8,9). Сравнение записи чисел в разных системах счисления представлено в таблице 3.

 

Таблица 3 – Сравнение записи чисел в трёх системах счисления

 

Десятичная	Восьмеричная	Двоичная
0	0	0
1	1	1
2	2	10
3	3	11
4	4	100
5	5	101
6	6	110
7	7	111
8	10	1000
9	11	1001
10	12	1010

 

 

Наиболее используемой системой счисления является десятичная система счисления, а для представления чисел в большинстве современных ЭВМ используется двоичная система счисления

 

Правило перевода числа из десятичной системы в двоичную систему счисления: перевод целой части – делением на основание системы, в которую переводим (на 2), а дробной части – умножением на это основание. Операции выполняются в десятичной системе. Остатки от деления собираются в обратном порядке.

 

Пример: перевести число 100 в двоичную систему счисления (рисунок 2).

Решение: представим перевод числа в виде столбца, каждая строка которого содержит частное и остаток от деления данного числа на основание двоичной системы счисления n = 2.

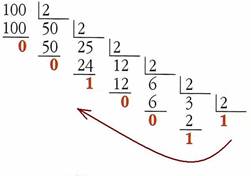Рисунок 2 – Перевод числа из десятичной системы в двоичную

 

 

В результате получим число 11001002 – результат перевода числа 10010 в двоичную систему счисления (индекс – основание системы счисления).

 

 

Как было уже сказано, в вычислительной технике используется двоичная система счисления (данные представляются в виде закодированной последовательности двоичных сигналов). Это обеспечивает высокую надёжность и помехоустойчивость вычислительной системы, так как в ней реализованы устройства лишь с двумя устойчивыми состояниями (чем проще устройство, тем оно надежнее).

При этом для описания логики функционирования аппаратных и программных средств используется алгебра логики (Булева алгебра). Она оперирует с логическими переменными, которые могут принимать тоже только два возможных значения (true — истина и false - ложь). Это очень удобно, так как обеспечивается универсальность (однотипность) процесса обработки информации на компьютере.

 

Скачано с www.znanio.ru