
Лекция
Тема: Показательная и логарифмическая функции, их свойства и графики.
Количество часов: 2 часа
Цель: расширение понятийной базы по теме «Функция» за счет включения в нее новых элементов; обобщить и систематизировать знания о логарифмической функции, ее свойствах; закрепить знания о логарифме числа; добиться усвоения обучающимися понятия логарифмической функции и ее свойства.
План:
1. Показательная функция и ее свойства
2. График показательной функции
3. Примеры построения графиков показательных функций
4. Логарифмическая функция и ее основные свойства.
5. График логарифмической функции и его построение.
Вопрос 1. Показательная функция и ее свойства
На доске запишем уравнения:
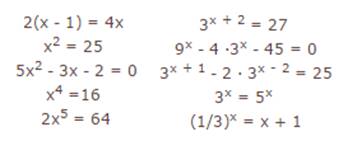
- Какие из данных уравнений вам знакомы, а какие нет?
- Да, действительно, уравнения второго столбика отнесла бы в одну группу – группу показательных уравнений, с которыми мы сегодня и должны познакомиться.
Показательная функция-это функция y(x)=ax, зависящая от показателя степени x, при некотором фиксированном значении основании степени a.
Рассмотрим показательную функцию y(x)=ax.
Будем считать, что основание степени a является положительным числом:
a >0.
Тогда функция y = axо пределена для всех x.
Ее область определения:- ∞ < x + ∞.
При a ≠ 1 она имеет множество значений:0< y < + ∞.
При a = 1 показательная функция является постоянной: y = 1
Показательная функция является монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
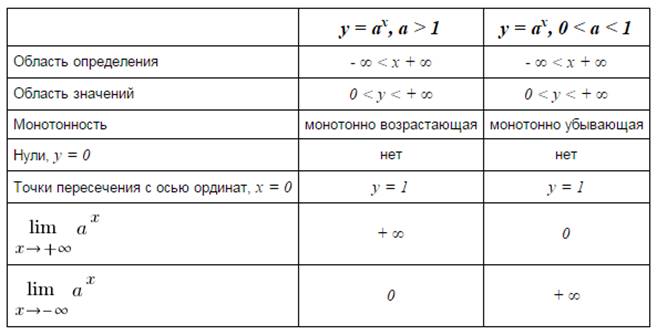
К общим свойствам показательной функции как при 0 < a < 1, так и при a>1 относятся:

Обратной для показательной функции с основанием степени a является логарифм по основанию a.
Если y
= ax (a >0, a ≠ 1), то![]() .
.
Если![]() (х>0, a>0,
a ≠ 1),
то х = ау
(х>0, a>0,
a ≠ 1),
то х = ау
Вопрос 2. График показательной функции
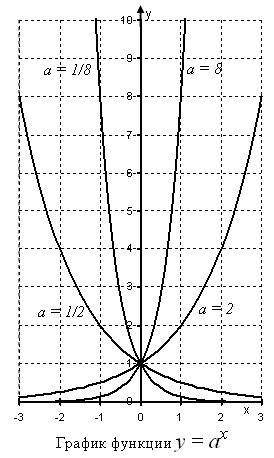
На графике представлены значения показательной функции y(x) = ax для четырех значений основания степени: a = 2, a = 8, a = ½ и a = 1/8.
На графике видно, что при a >1 показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост.
При 0 <a <1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем более сильное убывание.
Вопрос 3. Примеры построения графиков показательных функций
Пример 1. Построить график функции у = 2х
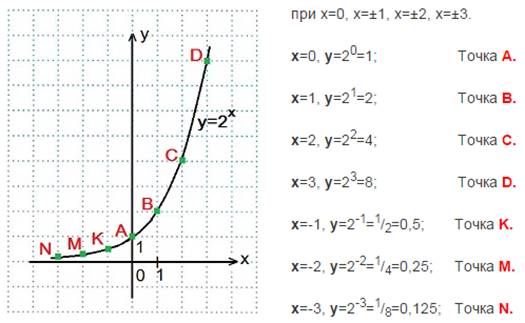
Большему значению аргумента х соответствует и большее значение функции у. Функция y=2 хвозрастает на всей области определения D(y)=R, так как основание функции 2>1.
Пример 2. Построить график функции у = (1/2)х
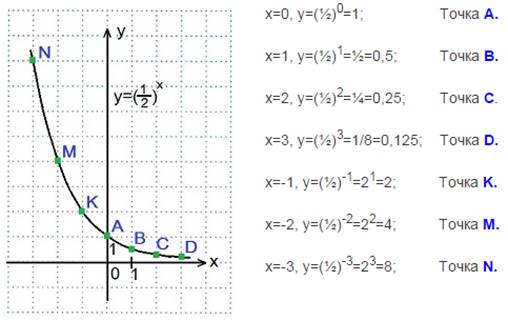
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D(y) = R, так как основание функции 0 < (1/2) < 1.
Вопрос 4. Логарифмическая функция и ее свойства.
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) - данная запись будет обозначать логарифм b по основанию а.
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
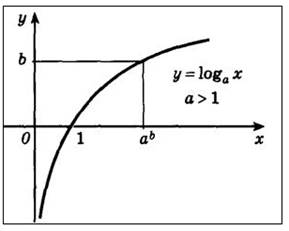
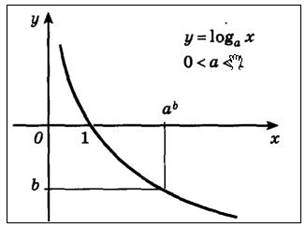
3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.
6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x< 1.
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
Вопрос 5. График логарифмической функции и его построение.
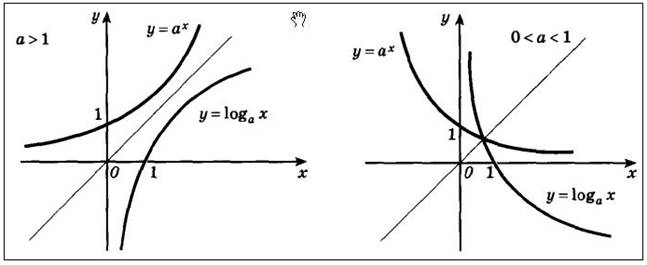
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.
Например: найти область определения логарифмической функции f(x) = log8(4 - 5*x).
Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 - 5*x>0. Решаем это неравенство и получаем x<0,8.
Таким образом, получается, что областью определения функции f(x) = log8(4 - 5*x) будет являться промежуток (-∞; 0,8)
Вопросы для самопроверки:
1. Какая функция называется показательной?
2. Перечислите основные свойства показательной функции y(x) = ax, a >1.
3. Перечислите основные свойства показательной функции y(x) = ax,0 <a <1.
4. Дайте определение логарифмической функции.
5. Перечислите основные свойства логарифмической функции.
6. Как связаны между собой графики показательной и логарифмической функции?
Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:
1. Башмаков М.И., Математика: учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. –7-е изд., стер. – М с.: Издательский центр «Академия», 2020. – 256с.
2. Григорьев С.Г. Математика: учебник для студ. учреждений сред. проф. организация/ С.Г.Григорьев, С.В.Иволгина; под ред. В.А.Гусева. – 14-е изд., стер. – М.: Издательский центр «Академия», 2019. – 416 с.
3. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни – 5-е изд. - М.: Просвещение, 2018. – 431 с.: ил.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.