
. Ф.И.О. учителя: ____Ткачук Наталья Петровна _________________________________________________________________________________________________
2. Класс: _8 Дата: __Предмет_-математика , № урока по расписанию:
|
3. Тема урока: Линейная функция1Свойства функции..4. Место и роль урока в изучаемой теме:. Урок закрепления знаний. Цель урока:Образовательная |
Уметь:строить график линейной функции; -определять, возрастающей или убывающей является линейная функция;находить с помощью графика промежутки знакопостоянства .Обобщить имеющиеся знания о линейной функции; найти новые сведения о линейной функции и её свойствах из различных источников информации; узнать, в каких областях знаний находит применение линейная функция;установить, находит ли применение линейная функция в повседневной жизни людей.Содействовать развитию умений применять полученные знания в нестандартных (типовых) условиях Развивающая: Способствовать развитию умений учащихся обобщать полученные знания, проводить анализ, синтез, сравнения, делать необходимые выводы. Содействовать развитию умений применять полученные знания в нестандартных и типовых условиях.
Воспитательная: Способствовать развитию творческого отношения к учебной деятельности
Характеристика этапов урока
|
Этап урока |
Цель |
Содержание учебного материала |
Методы |
ФОУД* |
Деятельность учителя |
Деятельность учеников |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Самоопределение.
|
Активизировать познавательную активность |
обобщить имеющиеся знания о линейной функции; найти новые сведения о линейной функции и её свойствах из различных источников информации; узнать, в каких областях знаний находит применение линейная функция; установить, находит ли применение линейная функция в повседневной жизни людей. Что такое функция. Как
называется Функция вида • Что обозначают k и b • Графиком функции вида у = kx +b является… • Составь формулу прямой (k = 2; b = -1) • (Охарактеризуй ее положение) • Как располагается прямая ,если b = 0 Продолжи правило • Для построения прямой необходимы только ….., так как через две….. |
словесный |
Фронтальная |
Приветствие учащихся. проведение. Создание ситуации готовности к уроку, успеха на предстоящем уроке. |
Проверяют готовность к уроку. Карточки для оценивания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2.Актуализация знаний . |
Выявить качество и уровень овладения знаниями и умениями, полученными на предыдущих уроках по теме |
Какие из функций линейные 1.у=-x+0,2; 8.y=12,4x-5,7 ; 2. y=-9x-18; 9.y=5,04x; 3.y=-5,04x; 10.y=126,35+8,75x; 4. y=x-0,2; 11.y=x:8; 5.y=0,005x; 12.y=133,1x; 6.y=3-10,01x; 13.y=2:x; 7.y=-0,0049; 14.y=х:62. ОГЭ №11 Что такое нули функции? Область значения? Найти нули функции. У=5х-10, у= 15-3х Соотнесите график функции и уравнение функции
А 1) 2) 3) 4) Как возникло понятие функция- Идея функциональной зависимости восходит к древности. Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно. Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт. Франсуа Виет Рене Декарт Кроме того, у Декарта и Ферма в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы. Рене Декарт Пьер Ферма |
Работа в группе |
Фронтальная. Гупповая-разбор алгоритмов решения задач;
|
При необходимости задает наводящие вопросы.
|
Отвечают на поставленные вопросы. Карточки для оценивания |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3.Постановка учебной задачи, целей урока. |
Формирование и развитие умения определять и формулировать проблему, цель и тему |
k – угловой коэффициент, b – свободный член. |
Работа в группе. Индивидуальная. |
Фронтальная. |
Какие действия мы проделали, чтобы узнать стоимость покупки? Какую тему мы будем изучать?
Побуждает к высказыванию своего мнения.
|
Высказываются. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Этап актуализации знаний по теме |
Содействовать развитию умений различать и сопоставлять линии. Обеспечить условия для развития умений грамотно, чётко и точно выражать свои мысли. |
1.
а) у= - 8 б) у=2 в) у= 0,5 г) у=0 ž Что можно сказать о этих прямых? ž у= -х+100 и у=-х+200.
1. Проходит ли график функции ( решение в парах каждый находит 1 точку) 2. а) у=2х-1 через точку А(3;5);В(1;1) б) у=-х+8 через точку B(-2;5); С(-1;9 через начало координат 1) у= 3х+4 2) у=-7х . 3. Будут ли прямые параллельны? а) у= 2х+3 и у= 3х+2; б) у=3х+4 и у= 3х-1; Каким будет угол наклона графика функции к положительному направлению оси ох? а) у=3х-5; б) у= -2х+5
№ зарядка : показать с пом рук возрастает. Убывает функция.. |
Работа с учнбником
Работа в парах с самопроверкой |
Фронтальная, индивидуальная. практикум по решению задач |
При необходимости задает наводящие вопросы . Проводит параллель с ранее изученным материалом. Обеспечивает мотивацию выполнения предложенных задач. Подводит обучающихся к выводу о существованию формул. |
Решают задачи , отвечают на вопросы учителя при необходимости Выполняют упражнение в тетради. По очереди комментируют, анализируют, определяют причины и способы решения. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5.Работа по самостоятельному применению полученных знаний. Актуализация знаний и умений в решении задач. |
Формирование и развитие умений чтения чисел.Планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, само регуляция |
3. |
Самостоятельная работа. Проверка соседа. |
«мозговой штурм», |
Контролирует выполнение работы. Осуществляет: индивидуальный контроль; выборочный контроль. Побуждает к высказыванию своего мнения. |
Решают задачи. Осуществляют: самооценку; ; взаимопроверку; выставляют предварительную оценку. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6.Оценка урока, самооценка.
|
Формирование и развитие умения анализировать и осмысливать свои достижения. Умение определять уровень овладения учебным материалом Оценка промежуточных результатов и само регуляция для повышения мотивации учебной деятельности |
Оценка на каждом этапе .
|
Работа в группе. |
Групповая и индивидуальная.. |
Побуждает к высказыванию своего мнения.
|
Осуществляют: самооценку и оценку товарища. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7.Итоги урока. Домашнее задание.
|
Умение соотносить цели и результаты собственной дея-тельности. Под-держание здоро-вого духа сопер-ничества для под-держания мотива-ции учебной дея-тельности; участие в коллективном обсуждении проблем. |
№ П. п |
Работа в группе. |
Фронтальная-Выделение и фор-мулиров-ание поз-навательной цели рефлексия спос-обов и условий действия Анализ и синтез объектов |
Побуждает к высказыванию своего мнения.
Дает комментарий к домашнему заданию; задание на поиск в тексте особенностей...
|
Дети участвуют в дискуссии, анализируют, проговаривают. Осмысливают и фиксируют свои достижения. -Сегодня на уроке я узнал… -сегодня на уроке я научился…
|
|
|
|
|
|
|
Раздаточный материал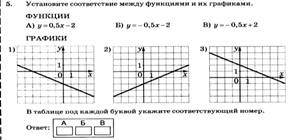
|
|
|
|
А) у=-2х-6 ,б) у=-2х+6, В)У=2х+6 |
а) у=-2х-6 ,б) у=-2х+6, В)У=2х+6 |
|
А) у=-2х-6 ,б) у=-2х+6, В)У=2х+6 |
А) у=-2х-6 ,б) у=-2х+6, В)У=2х+6
|
|
1.Проходит ли график функции а) у=2х-1 через точку А(3;5); В(1;1) б) у=-х+8 через точку B(-2;5); С(-1;9) 2.Проходит через начало координат. 1) у= 3х+4 2) у=-7х 3. Будут ли прямые параллельны? а) у= 2х+3 и у= 3х+2; б) у=3х+4 и у= 3х-1; 4.Каким будет угол наклона графика функции к положительному направлению оси ох? а) у=3х-5; б) у= -2х+5
|
1.Проходит ли график функции а) у=2х-1 через точку А(3;5); В(1;1) б) у=-х+8 через точку B(-2;5); С(-1;9) 2.Проходит через начало координат. 1) у= 3х+4 2) у=-7х 3. Будут ли прямые параллельны? а) у= 2х+3 и у= 3х+2; б) у=3х+4 и у= 3х-1; 4.Каким будет угол наклона графика функции к положительному направлению оси ох? а) у=3х-5; б) у= -2х+5
|
|
1.Проходит ли график функции а) у=2х-1 через точку А(3;5); В(1;1) б) у=-х+8 через точку B(-2;5); С(-1;9) 2.Проходит через начало координат. 1) у= 3х+4 2) у=-7х 3. Будут ли прямые параллельны? а) у= 2х+3 и у= 3х+2; б) у=3х+4 и у= 3х-1; 4.Каким будет угол наклона графика функции к положительному направлению оси ох? а) у=3х-5; б) у= -2х+5
|
1.Проходит ли график функции а) у=2х-1 через точку А(3;5); В(1;1) б) у=-х+8 через точку B(-2;5); С(-1;9) 2.Проходит через начало координат. 1) у= 3х+4 2) у=-7х 3. Будут ли прямые параллельны? а) у= 2х+3 и у= 3х+2; б) у=3х+4 и у= 3х-1; 4.Каким будет угол наклона графика функции к положительному направлению оси ох? а) у=3х-5; б) у= -2х+5
|
|
задания |
ответ |
самооценка |
Оценка товарища |
Итоговая отметка |
||||||||
|
Какие из функций линейные |
|
|
|
|
||||||||
|
Установите соответствие функциями и графиками. |
|
|
|
|
||||||||
|
Проходит ли график функции ( решение в парах каждый находит 1 точку) |
|
|
|
|
||||||||
|
Установите соответствие между угловым коэффициентом и графиком. |
|
|
|
|
||||||||
|
Установите соответствие функциями и графиками. Задайте формулой график |
|
|
|
|
||||||||
|
Количество верных ответов |
|
|
|
|
|
задания |
ответ |
самооценка |
Оценка товарища |
Итоговая отметка |
||||||||
|
Какие из функций линейные |
|
|
|
|
||||||||
|
Установите соответствие функциями и графиками. |
|
|
|
|
||||||||
|
Проходит ли график функции ( решение в парах каждый находит 1 точку) |
|
|
|
|
||||||||
|
Установите соответствие между угловым коэффициентом и графиком. |
|
|
|
|
||||||||
|
Установите соответствие функциями и графиками. Задайте формулой график |
|
|
|
|
||||||||
|
Количество верных ответов |
|
|
|
|
ОДА ФУНКЦИИ
На первый взгляд, понятие не ново,
И не всегда подумаешь о том,
Как важно будет в жизни это слово
И сколько смысла будет в слове том!
Его по-разному с годами толковали.
Сам Лобачевский руку приложил,
Чтоб слово «функция» и в средней школе знали,
Чтоб каждый ученик им дорожил!
Без функции не сдашь простой экзамен,
Без функции ты не войдешь в предмет!
Без функции не разгорится пламя!
Без функций никакой науки нет!
И. Кушнир, Л. Финкельштейн
* * *
Идея функциональной зависимости восходит к древности. Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.
Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт. Франсуа Виет Рене Декарт
Кроме того, у Декарта и Ферма в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы. Рене Декарт Пьер Ферма
Само слово «функция» впервые было употреблено немецким математиком Лейбницем в 1673г. В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667-1748) который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных». Готфрид Вильгельм Лейбниц Иоганн Бернулли
Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного») Так понимали функцию на протяжении почти всего 18 века Даламбер, Лагранж и другие видные математики. Д’Аламбер Жан Лерон Леонард Эйлер Жозеф Луи Лагранж
Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать
под функцией, внес французский математик Жан Батист Жозеф Фурье. Батист Жозеф Фурье
Таким образом, современное определение функции, свободное от упоминании об аналитическом задании, обычно приписываемое немецкому математику П.Л. Дирихле (1805-1859), неоднократно предлагалось и до него. Дирихле Петер Густав Лежён
Источник: https://needlewoman.ru/articles/skazka-o-lineynoy-funktsii.html
Как возникло понятие «линейная функция»
Функция – одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Высокого уровня математические знания достигли в Древнем Вавилоне. Для облегчения вычислений при учёте налогов, возведении своих дворцов и т.д. вавилоняне составили громоздкий комплект специальных арифметических таблиц: таблицы обратных значений чисел, таблицы квадратов и кубов и даже таблицы для суммы квадратов чисел и их кубов. Однако путь от появления таблиц до создания общего понятия функциональной зависимости был ещё очень долог.
В Древней Греции в отличие от Вавилона появились профессиональные ученые, которые изучали саму математическую науку. Древнегреческие математики нашли много различных кривых, неизвестных вавилонянам, изучали зависимости между отрезками диаметров и хорд в круге, эллипсе и других линиях, но всё же не создали общего понятия функции.
Только начиная с XVII века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.
Путь к появлению понятия функции заложил в XVII веке французский философ и математик Рене Декарт (1596–1650). Он первый ввёл в математику понятие переменной величины. Чтобы освободить алгебру от геометрического языка, Декарт ввёл фиксированный единичный отрезок и стал рассматривать отношение других отрезков к нему. Он установил соответствия между числами и отрезками на прямой и, таким образом, ввел алгебраический метод в геометрию. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа – отрезками. При записи зависимостей между величинами, он стал применять буквы: для переменных и неизвестных величин Декарт принял обозначения x, y, z, …, а для величин известных и постоянных – a, b, c и т.д. Как известно, эти обозначения применяются в математике до сегодняшнего дня. Отношения между известными и неизвестными величинами Декарт выражал в виде уравнений, в которых все величины заменил длинами отрезков. Он обратил внимание на то, что кривая на плоскости характеризуется уравнением, обладающим тем свойством, что координаты любой точки, лежащей на этой линии, удовлетворяют данному уравнению. Одновременно с Декартом к мысли о соответствии между линиями и уравнениями пришел другой французский математик Пьер Ферма (1601–1665). В их работах появляется отчетливое представление прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы.
В 1671 году И. Ньютон (1643–1727) под функцией стал понимать переменную величину, которая изменяется с течением времени (он называл её «флюентой»).
Но у Декарта, как и у его современников, понятие функции носило по существу интуитивный характер и было связано либо с геометрическими (ординаты точек кривых – функция от абсцисс x), либо с механическими (путь и скорость – функция от времени t) представлениями.
Само слово «функция» (от латинского functio – совершение, выполнение) впервые было употреблено немецким математиком Лейбницем (1646–1716) в 1673 г. в письме к Х. Гюйгенсу (1629–1695) (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), а в печати введено с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа».
В XVIII веке появился новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667–1748), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Леонард Эйлер. «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего 18 века французские математики Жан Лерон Даламбер (1717–1783), Жозеф Луи Лагранж (1736–1813), Жан Батист Жозеф Фурье (1768–1830) и другие видные математики.
Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых XVIII века по поводу того, что стоит понимать под функцией, внёс Фурье. Из его трудов следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения, и что имеются также прерывные кривые, изображаемые аналитическим выражением.
После работы Фурье стало ясно, что несущественно, каким аналитическим выражением задана функция, что это только, как говорят философы, кажимость (от слова «казаться»). А существо дела в том, какие значения принимает функция при заданных значениях аргумента. После длительного уточнения этой идеи, в которой приняли участие Фурье, Н.И. Лобачевский (1792–1856), немецкий математик Иоганн Дирихле (1805–1859) и другие ученые, общепризнанным стало следующее определение: переменная величина у называется функцией переменной величины х, если каждому значению величины х соответствует единственное определенное значение величины у.
Источник: https://needlewoman.ru/articles/skazka-o-lineynoy-funktsii.html
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.