Филиал бюджетного профессионального образовательного учреждения Чувашской Республики

 «Чебоксарский медицинский колледж»

Министерства здравоохранения Чувашской Республики в городе Канаш

Методическая разработка теоретического занятия

Элементы математической статистики.

Таблицы, диаграммы, графики.

учебная дисциплина БД. 04 Математика

специальность 34.02.01Сестринское дело

(базовая подготовка)

Канаш, 2021

Аннотация

            Данная методическая разработка по теме «Элементы математической статистики. Таблицы, диаграммы, графики.» является уроком изучения нового материала. Урок построен так, чтобы обучающиеся, опираясь на ранее полученные знания, могли вывести формулы сами. Материал урока направлен на решение элементарные комбинаторные задачи, связанные с составлением различный соединений из имеющихся элементов.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 3

1. МЕТОДИЧЕСКИЙ БЛОК.. 4

1.1. Учебно-методическая карта. 4

1.2. Технологическая карта. 8

2.ИНФОРМАЦИОННЫЙ БЛОК 10

2.1. План лекции. 10

2.2.Теоретическая часть. 11

2.3. Глоссарий. 18

3. КОНТРОЛИРУЮЩИЙ БЛОК.. 19

ВВЕДЕНИЕ

        Данная методическая разработка по теме «Элементы математической статистики. Таблицы, диаграммы, графики» является уроком изучения нового материала. Урок построен так, чтобы обучающиеся, опираясь на ранее полученные знания, могли вывести формулы сами. Материал урока направлен на развитие логического мышления, алгоритмической культуры, интуиции, навыков исследовательской деятельности, творческих способностей обучающихся. Структура урока: постановка цели и задач урока; повторение умений и навыков, являющихся опорой для восприятия новой темы; проведение проверочных упражнений (устная работа); Упражнения на закрепление данного алгоритма;  тренировочные упражнения по образу и подобию в виде самостоятельной работы; самоконтроль обучающихся.
         Создание проблемных ситуаций на уроках математики повышает интерес к предмету, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность.

1. МЕТОДИЧЕСКИЙ БЛОК

1.1. Учебно-методическая карта

1.2. Технологическая карта

Структура комбинированного урока

2. информационный блок

2.1. План лекции

2.2. Теоретическая часть.

       Проверка домашнего задания
Провести фронтальный опрос в виде ответов на вопросы:

            Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

Случайные величины, как правило, обозначают через  *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .

* Иногда используют , а также греческие буквы

Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:

 – количество очков, которое выпадет после броска игрального кубика.

В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина  может принять одно из следующий значений:

.

Пример из статьи о Статистическом определении вероятности:

 – количество мальчиков среди 10 новорождённых.

Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:

, либо  мальчиков – один и только один из перечисленных вариантов.

И, дабы соблюсти форму, немного физкультуры:

 –  дальность прыжка в длину (в некоторых единицах).

Её не в состоянии предугадать даже мастер спорта :)

Тем не менее, ваши гипотезы?

Коль скоро речь идёт о множестве действительных чисел, то случайная величина  может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.

Таким образом, случайные величины целесообразно разделить на 2 большие группы:

1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

…нарисовались непонятные термины? Срочно повторяем основы алгебры!

2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.

Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ

Сначала разберём дискретную случайную величину, затем – непрерывную.

Поехали:

Закон распределения дискретной случайной величины

– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:

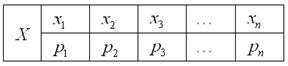
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».

А теперь очень важный момент: поскольку случайная величина  обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

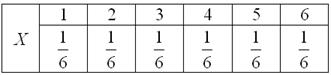
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

Пример 1

Некоторая игра имеет следующий закон распределения выигрыша:

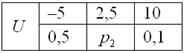
Найти 

            наверное, вы давно мечтали о таких задачах :) Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина  может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

Разоблачаем «партизана»:

 – таким образом, вероятность выигрыша  условных единиц составляет 0,4.

Контроль: , в чём и требовалось убедиться.

Ответ: 

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

Пример 2

В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины  – размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно  рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению:
 – вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

С остальными случаями всё просто. Вероятность выигрыша  рублей составляет:

И для :

Проверка:  – и это особенно приятный момент таких заданий!

Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

Пример 3

Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины  – количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились :) Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание дискретной случайной величины

Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина  принимает значения  с вероятностями  соответственно. Тогда математическое ожидание  данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

Вычислим, например, математическое ожидание случайной величины  – количества выпавших на игральном кубике очков:

 очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

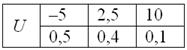
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

, таким образом, математическое ожидание данной игры проигрышно.

Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры :) Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Пример 4

Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины  – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

Пример 5

Случайная величина  задана своим законом распределения вероятностей:

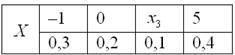
Найти , если известно, что . Выполнить проверку.

Есть?

Решения и ответы:

Пример 3. Решение: по условию  – вероятность попадания в мишень. Тогда:
 – вероятность промаха.

Составим  – закон распределения попаданий при двух выстрелах:

 – ни одного попадания. По теореме умножения вероятностей независимых событий:

 – одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

 – два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ: 

Примечание: можно было использовать обозначения  – это не принципиально.

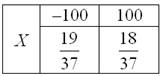
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид:

Вычислим математическое ожидание:

Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания:

поменяем части местами и проведём упрощения:

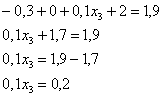
таким образом:

Выполним проверку:

, что и требовалось проверить.

Ответ: 

              В статистике исследуют различные совокупности данных — числовых значений случайных величин с учётом частот, с которыми они встречаются в совокупности.

Набор всех данных назовём генеральной совокупностью, а любую её часть — выборкой.

В статистических исследованиях выборку называют репрезентативной, если в ней присутствуют те и только те значения случайной величины, что и в генеральной совокупности, причём частоты имеющихся в ней данных находятся практически в тех же отношениях, что и в генеральной совокупности.

Совокупность данных иногда нужно оценить одним числом. Мерой центральной тенденции может являться среднее, мода или медиана.

Мода (обозначают Mo) — это значение случайной величины, имеющее наибольшую частоту в рассматриваемой выборке.

Пример:

мода выборки 7, 6, 2, 5, 6, 1 равна 6;

a выборка 2, 3, 8, 2, 8, 5 имеет две моды: Mo =2,  Mo =8.

         Медиана (обозначают Me) — это число (значение случайной величины), разделяющее упорядоченную выборку на две равные по количеству данных части.

         Если в упорядоченной выборке нечётное количество данных, то медиана равна серединному из них. Если в упорядоченной выборке чётное количество данных, то медиана равна среднему арифметическому двух серединных чисел.

Пример:

1) 5, 9, 1, 4, 5, −2, 0;   2) 7, 4, 2, 3, 6, 1.

1. Расположим элементы выборки в порядке возрастания: −2, 0, 1, 4, 5, 5, 9. Количество данных нечётно. Слева и справа от числа 4 находятся по 3 элемента, т. е. 4 — серединное число выборки, поэтому Me =4.

2. Упорядочим элементы выборки: 1, 2, 3, 4, 6, 7.

Количество данных чётно. Серединные данные выборки: 3 и 4 — поэтому Me=3+42=3,5.

Среднее (или среднее арифметическое) выборки — это число, равное отношению суммы всех чисел выборки к их количеству.

Если рассматривается совокупность значений случайной величины X, то её среднее обозначают X.

Пример:

найти среднее выборки значений случайной величины X, распределение которых по частотам представлено в таблице:

X =2⋅1+3⋅2+4⋅3+8⋅1+10⋅11+2+3+1+1=388=4,75.

Одной из наиболее распространённых характеристик выборки значений случайной величины, чьё распределение по вероятностям известно, является так называемое математическое ожидание.

Пусть распределение по вероятностям P значений некоторой случайной величины X задано таблицей.

Тогда число E, где E=X1⋅P1+X2⋅P2+...+Xn−1⋅Pn−1+Xn⋅Pn, называют математическим ожиданием (или средним значением) случайной величины X.

4. Решение задач упражнения 1184,1201 - 1203 (не четные).

5. Домашнее задание. Решение 1184,1201 - 1203 – четные пункты.

2.3. Глоссарий

4.      Контролирующий блок

Пример 1. Дискретная случайная величина имеет ряд распределения

Найти математическое ожидание и дисперсию.

Пример 2. Дискретная случайная величина имеет ряд распределения.

Найти математическое ожидание и дисперсию.

Пример 3.

Задан закон распределения дискретной случайной величины X.

Найти неизвестную вероятность p, математическое ожидание M и дисперсию, построить многоугольник распределения.

Пример 4.

Найти р2 и р4, если р4 в 6 раз больше р2, если задана дискретная случайная величина Х и имеется закон распределения.  Найти математическое ожидание и дисперсию дискретной случайной величины.

Пример 5.

Выигрыши, которые приходятся на один билет в каждой из двух лотерей, имеют следующие законы распределения:

Пример 6. Находить   моду, медиану, среднее арифметическое выборки, размах выборки.

1.       Найти моду: 1,3,5,1,4,3,2

2.       Найти медиану выборки 4,1,8,9,13,10

3.       Найти среднее арифметическое значение выборки и размах выборки 24, -5, 13, -8

4.       Какой из лотерей вы отдадите предпочтение? Найти математическое ожидание и дисперсию.

4.Оформить отчет.

По результатам решения тренажера выставляется оценка, которая учитывается при приеме зачета.

Шкала оценки образовательных достижений

Скачано с www.znanio.ru