математика

ПОУРОЧНЫЕ РАЗРАБОТКИ ПО МАТЕМАТИКЕ 6 КЛАСС

ГЛАВА I. ОБЫКНОВЕННЫЕ ДРОБИ

§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (22 ч)

ОСНОВНОЕ СВОЙСТВО ДРОБИ (2 ч)

Урок 22. Основное свойство дроби

Цели: учить применять основное свойство дроби при выполнении заданий; развивать грамотную математическую речь; совершенствовать сочетание индивидуальной и коллективной форм работы с учащимися; проверить знания и навыки учащихся по изученному материалу.

Ход урока

I. Организационный момент

II. Устный счет

1. В Древнем Риме при измерении величин применялись дроби со знаменателем 12.

Вместо 1/12 говорили «одна унция», вместо 5/12 - «пять унций» и т. д. Выразите в унциях: половину, треть, четверть, пять шестых, три четверти. (Половина — 6 унции, треть — 4 унции, четверть — 3 унции, пять шестых — 10 унций, три четверти — 9 унций.)

2. Укажите среди данных произведений разложение числа 500 на простые множители: а) 25 · 2 · 10; б) 2 · 2 · 2 · 5 · 5 · 5; в) 4 · 5 · 5 · 5; г) 2 · 2 · 5 · 5 · 5.

3. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 6 и 8; б) 12 и 20; в) 24 и 48; г) 5 и 7; д) 12 и 15; е) 1 и 50.

4. Задание на развитие памяти.

Посмотрите 15 сек надроби и попробуйте их запомнить: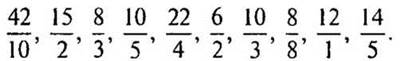 

— Запишите в тетрадь, какие дроби вы запомнили.

— Проверьте.

— Если запомнили больше половины, то хорошо.

— Выделите целую часть из неправильных дробей, записанных на доске.

5. Замените каждую из следующих дробей дробью, знаменатель которой равен 20.

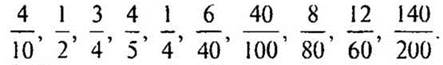
6. Заяц вытащил 8 морковок и съел их все, кроме 5. Сколько морковок осталось? (5.)

III. Индивидуальная работа

2 человека работают у доски по индивидуальным карточкам, в это время с остальными учащимися проводится устная работа. В конце работы всем учащимся предлагается проверить правильность выполнения заданий.

1 карточка

1. Найдите все делители числа и расположите их в порядке убывания: а) 40: б) 51; в) 17.

2. Разложите число на простые множители: а) 60; б) 500: в) 196.

2 карточка

1. Найдите все делители числа и расположите их в порядке убывания: а) 50: б) 21; в) 13.

2. Разложите число на простые множители: а) 80; б) 300; в) 135.

IV. Сообщение темы урока

— Сегодня мы будем учиться применять основное свойство дроби при выполнении различных заданий.

V. Закрепление изученного материала

1. № 213 стр. 36 (работа в парах).

(Во время обсуждения решения подойти к ребятам, послушать их ответы. Попросить более сильных учащихся, объяснить решения слабым ученикам. Отвечают слабые ученики).

2. Практическая работа.

№ 238 стр. 38 (на доске и в тетрадях).

(Ответ: координатами одной и той же точки являются числа: .)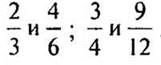

— Запишите соответствующие равенства: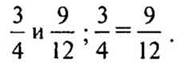 

— Прочитайте равенство двух дробей разными способами. (Дробь две третьих равна дроби четыре шестых: дроби две третьих и четыре шестых равны; две третьих равны четырем шестым.)

3. № 237 стр. 38 (самостоятельно).

— Что можете сказать о получившихся дробях? (Равны.)

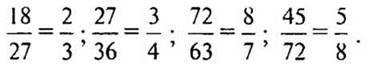
4. № 218 стр. 36 (устно).

— Что нужно сделать, чтобы ответить на вопрос задачи? (Сначала 12 разделить на знаменатель, затем числитель умножить на получившееся число.)

Решение:

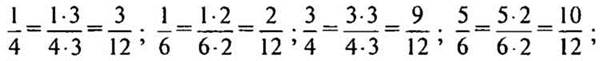
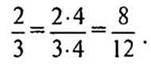
— Сколько двадцатичетвертых долей содержится в данных дробях?

Решение:

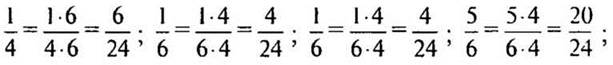
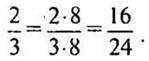
5. № 219 (устно).

— Назовите еще по три дроби, равные данным дробям.

6. Объясните, почему верны равенства:

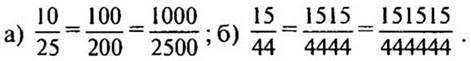
VI. Физкультминутка

VII. Работа над задачей

1. а) Выберите правильное утверждение:

A) Скорость — это расстояние между двумя точками.

Б) Скорость — это расстояние, пройденное телом за единицу времени.

B) Скорость — это быстрая езда.

б) Выберите правильное утверждение:

A) Чтобы найти расстояние, надо скорость разделить на время.

Б) Чтобы найти расстояние, надо время разделить на скорость.

B) Чтобы найти расстояние, надо скорость умножить на время.

2. № 233 (2) стр. 38 (после разбора самостоятельно).

— Прочитайте задачу.

— Как найти расстояние, зная скорость и время? (Чтобы найти расстояние, надо скорость умножить на время.)

— Как найти время, зная расстояние и скорость? (Чтобы найти время, надо расстояние разделить на скорость.)

Решение:

1) 5,2 · 4,5 = 23,4 (км) — прошли по дороге.

2) 32,4 - 23,4 = 9 (км) — осталось пройти.

3) 9 : 2,5 = 90 : 25 = 3,6 (ч) — шли по болотистой местности.

4) 4,5 + 1,6 + 3,6 = 9,7 (ч) — затрачено на весь поход.

(Ответ: 9,7 ч.)

3. № 232 стр. 37 (самостоятельно, устное обсуждение решения). Решение:

1) 12 · 11 · 10 · 9 = 132 · 90 = 11 880 (способами) - можно составить команду из 4 человек, но где встречаются перестановки из 4 человек.

2) 4 · 3 · 2 · 1 = 24 (перест.) - встречаются в данных способах.

3) 11 880 : 24 = 495 (способов) — можно составить команду из 4 человек.

4) 4 · 3 · 2 · 1 = 24 (сп.) - распределить этапы эстафеты.

(Ответ: 11 880 способами; 24 способами.)

VIII. Закрепление изученного материала

1. Между какими последовательными натуральными числами заключено число: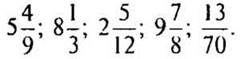 

Ответ можно записать в виде неравенства или написать только два натуральных числа.

(Ответ: )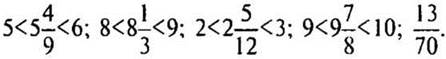

Последняя дробь больше нуля, но нуль не является натуральным числом, поэтому ответить на данный вопрос нельзя.

2. № 230 (б) стр. 37 (самостоятельная работа с последующей взаимопроверкой).

Решение:

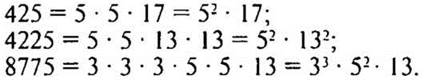
— Назовите простые числа, которые удовлетворяют неравенству 1 < а < 23.

(Первым трем ответившим ученикам можно поставить оценку.)

3. № 231 стр. 37 (у доски и в тетрадях).

Решение:

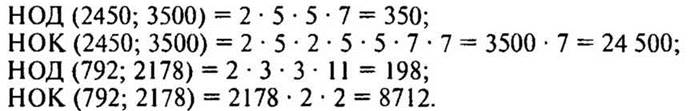
4. № 235 стр. 38.

— Как удобнее сосчитать?

— Какое свойство умножения использовали? (Распределительное.)

— Запишите его в буквенном виде.

Распределительный закон умножения относительно сложения: 

Распределительный закон умножения относительно вычитания: 

— Чтобы умножить число на 0,25, можно это число разделить на 4.

5. Найдите значение выражений:

Решение:

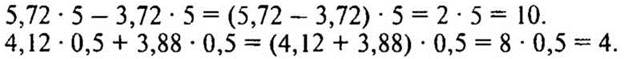
IX. Самостоятельная работа (10 мин)

Вариант I

1. Запишите две дроби, равные: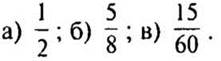 

2. В равенстве вместо буквы запишите такое число, чтобы равенство было верным: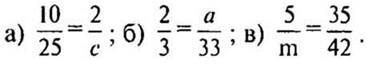 

3. Сравните числа: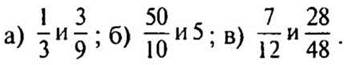 

Вариант II

1. Запишите две дроби, равные: 

2. В равенстве вместо буквы запишите такое число, чтобы равенство было верным: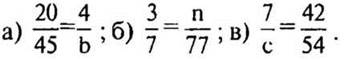 

3. Сравните числа: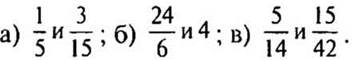 

X. Подведение итогов урока

— В чем состоит основное свойство дроби?

— Назовите его для дробей: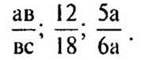 

— Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3?

Домашнее задание: № 220, 221 (в, г) стр. 36; № 239 (б), 240 (б, г), 241 (б) стр. 38.

По желанию № 229 стр. 37.

ПОУРОЧНЫЕ РАЗРАБОТКИ ПО МАТЕМАТИКЕ 6 КЛАСС

ГЛАВА I. ОБЫКНОВЕННЫЕ ДРОБИ

§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (22 ч)

1.СОКРАЩЕНИЕ ДРОБЕЙ (3 ч)

Информация для учителя

Способы сокращения дробей

I  способ

С помощью признаков делимости найти общий делитель числителя и знаменателя дроби.

Делить числитель и знаменатель дроби на общий делитель до тех пор, пока не получится несократимая дробь.

II способ

Найти наибольший общий делитель числителя и знаменателя.

Разделить числитель и знаменатель дроби на наибольший общий делитель.

В результате деления получится несократимая дробь.

III способ

Разложить числитель и знаменатель на несколько множителей.

Разделить числитель и знаменатель на данные равные множители.

Сокращать до тех пор, пока не получится несократимая дробь.

При сокращении можно использовать любой удобный способ.

Урок 23. Сокращение дробей

Цели: ввести понятие сокращения дробей и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби; отрабатывать умение решать задачи на движение по воде; развивать умение самостоятельно мыслить.

Ход урока

I. Организационный момент

II. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 12 и 8; б) 9 и 15; в) 11 и 44; г) 8 и 20; д) 12 и 20; е) 10 и 15.

2. Замените каждую из следующих дробей дробью, знаменатель которой равен 36.

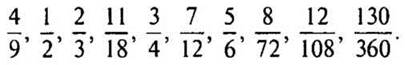
3. Найдите длину отрезка, если

а)    половина его равна 8 см;

б)    треть длины отрезка равна 5 см;

в)    четверть равна 6 см;

г)    шестая часть длины отрезка равна 2 см.

4. Маша ходит на каток раз в 2 дня, Оля - в 3 дня и Катя — в 4 дня. Они все вместе встретились на катке в субботу. Через сколько дней они встретятся опять? (12 дней.)

5. Имеются две банки: 3 л и 5 л. Как с помощью таких сосудов набрать из водопроводного крана 4 л воды?

III. Индивидуальная работа

1 карточка

1. Найдите наибольший общий делитель чисел: а) 12 и 48; б) 14 и 35; в) 5 и 17; г) 40 и 60.

2. Найдите наименьшее общее кратное чисел: а) 54 и 27; б) 19 и 3; в) 45 и 54.

2 карточка

1. Найдите наибольший общий делитель чисел: а) 27 и 36; б) 15 и 45; в) 3 и 19; г) 90 и 60.

2. Найдите наименьшее общее кратное чисел: а) 64 и 72; б) 17 и 5; в) 14 и 52.

IV. Сообщение темы урока

— Прочитайте тему урока. Мы сегодня будем сокращать дроби, а в этом нам помогут: основное свойство дроби и признаки делимости чисел.

— А знаете, как в первых учебниках математики XVII века назывались дроби? (Ломаные числа).

V. Изучение нового материала

1. Подготовительная работа.

— Какие числа называются взаимно простыми.

— Приведите примеры взаимно простых чисел. (2 и 5, 4 и 9, 15 и 28 и т.д.)

2. № 261 стр. 42 (устно).

— На основании чего мы можем умножать числитель и знаменатель дроби? (На основании основного свойства дроби.)

Решение:

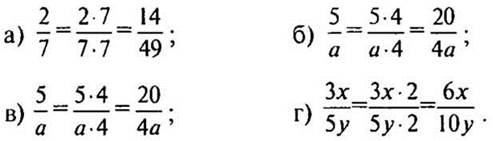
3. Работа над новой темой.

— Дана дробь 24/36. На какие числа можно разделить числитель и знаменатель дроби? (На 2, 3, 4, 6, 12.)

— Разделите числитель и знаменатель дроби 24/36 на наибольший общий делитель числителя и знаменателя, на 12.

— Какая получилась дробь? (2/3.)

— Сравните дроби 24/36 и 2/3. (Они равные, т. е. 24/36 = 2/3.)

— Такое преобразование называется сокращением дроби.

Определение. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.

— При сокращении дроби ее числовое значение не меняется, изменилась только ее запись.

— Можно ли еще сократить дробь 2/3? (Нет.)

— Что можете сказать о числах 2 и 3? (Они взаимно простые.)

— Если дробь больше сократить нельзя, то ее называют несократимой.

— Дайте самостоятельно определение несократимой дроби.

Определение. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой.

— Рассмотрим способы сокращения дробей.

135

— Дана дробь 135/180.

I способ

— Сокращать дроби можно постепенно, используя признаки делимости.

— Назовите общие делители чисел. (3 и 5.)

— Можно сначала числитель и знаменатель дроби разделить на 3, потом на 5 и т.д., а можно, наоборот, разделить сначала на 5, потом на 3.

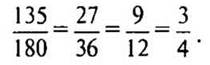
— Как называется дробь 3/4? (Несократимой.)

— Почему? (Числа 3 и 4 взаимно простые.)

II способ

— Найдите наименьший общий делитель числителя и знаменателя дроби. (НОД (135; 180) = 45.)

— Разделите числитель и знаменатель дроби на 45. (135/180 = 3/4.)

III способ

— Разложим числитель и знаменатель на несколько множителей.

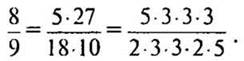
— Сократим дробь на произведение общих множителей. (На 3 · 3 · 5.)

— Получим несократимую дробь 3/4.

VI. Физкультминутка

VII. Закрепление изученного материала

1. Назовите несократимые дроби: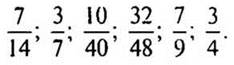 

— Почему эти дроби являются несократимыми?

2. № 242 стр. 39 (под руководством учителя с подробным комментированием).

— Назовите наибольший делитель числителя и знаменателя.

— Разделите числитель и знаменатель данной дроби на их общий делитель.

— Как называется получившаяся дробь? (Несократимая.)

Решение:

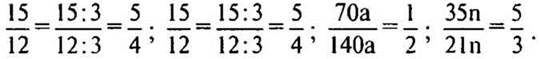
3. № 246 стр. 40 (после краткого разбора самостоятельно, с последующей проверкой).

— Сколько минут в 1 ч? (60 мин.)

— Какую часть часа составляет 1 мин? (1 мин = 1/60 ч.)

VIII. Самостоятельная работа

Вариант I

1. Запишите дроби в виде несократимой обыкновенной дроби: 0,4; 0,88; 0,025; 0,004; 0,0125.

2. Какую часть:

а) метра составляют 8 дм;

б) килограмма составляют 45 г;

в) километра составляют 64 м;

г) тонны составляют 75 ц.

Вариант II

1. Запишите дроби в виде несократимой обыкновенной дроби: 0,6; 0,36; 0,075; 0,008; 0,0025.

2. Какую часть:

а) сантиметра составляют 4 мм;

б) центнера составляют 16 кг;

в) дециметра составляют 6 см;

г) тонны составляют 25 ц.

(Учитель выборочно проверяет тетради.)

IX. Работа над задачей

1. а) Один рабочий изготовил за 4 ч 12 деталей.

— Какие вопросы можно задать, чтобы данное высказывание стало задачей? Ответьте на них.

— Сколько деталей изготавливал рабочий за 1 ч? (12 : 4 = 3 (д.) — за 1 ч.)

— Сколько времени тратил рабочий на изготовление 1 детали?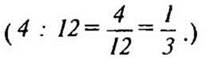 

б) № 250 стр. 40 (у доски и в тетрадях).

— Прочитайте задачу.

— Что известно?

— Что неизвестно?

— Можно сразу ответить на вопрос задачи?

Решение:

1) Сколько времени тратил первый рабочий на изготовление одной детали?

(Ответ: )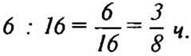

2) Сколько времени тратил первый рабочий на изготовление одной детали?

(Ответ: )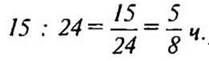

3) Какой из рабочих тратил на изготовление детали больше времени?

(Ответ: 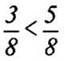 (второй рабочий).)

4) На сколько больше времени тратил второй рабочий на изготовление одной детали, чем первый?

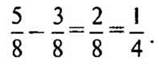
(Ответ: на 1/4.)

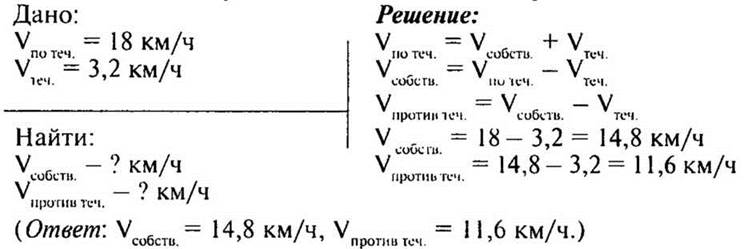
2. Собственная скорость катера 12 км/ч. Скорость течения реки 3 км/ч. Найдите скорость катера по течению и против течения реки.

(Можно записать на доске текст задачи, а можно предложить самостоятельно составить задачу по краткой записи).

— Составьте задачу о движении по воде по краткой записи.

— Как найти скорость по течению и против течения реки, зная собственную скорость и скорость течения?

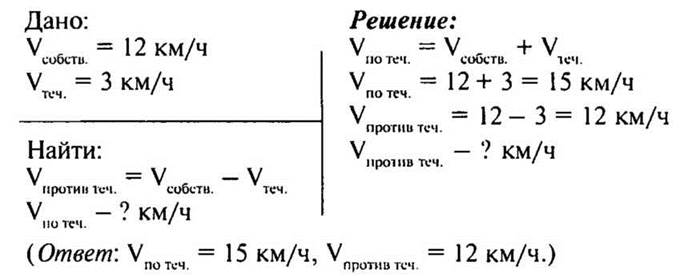
X. Подведение итогов урока

— Какую дробь называют несократимой?

— Приведите примеры несократимых дробей.

— На каком свойстве основано сокращение дробей

Домашнее задание: № 268 (а) стр. 42; № 270, 274 (а) стр. 43; № 263 стр. 42.

Дополнительный материал

Старинная задача

На дворе бегают куры и поросята. У всех вместе 20 голов и 52 ноги. Сколько всего кур и сколько поросят?

I  способ

Решение методом перебора:

II способ

Решение:

Пусть ног у поросят и кур будет поровну, по 2.

2  · 20 = 40 (ног) — без двух ног у каждого поросенка.

52 — 40 = 12 (ног) — лишних на всех поросят.

12 : 2 = 6 (поросят).

20 — 6 = 14 (кур).

(Ответ: 14 кур, 6 поросят.)

§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (22 ч)

1.СОКРАЩЕНИЕ ДРОБЕЙ (3 ч)

Урок 24. Сокращение дробей

Цели: отрабатывать умение сокращать дроби; закреплять умение решать задачи на движение по воде; расширять кругозор и математическую культуру учащихся; развивать умение самостоятельно работать.

Ход урока

I. Организационный момент

II. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 25 и 40; 55 и 60; 4 и 15; 8 и 36; 18 и 72; 15 и 60; 9 и 12; 45 и 60.

2. Сократите дроби: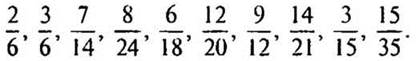 

3. Выразите неизвестные переменные: 

Эти вопросы (можно выборочно) задаются в том случае, если учащиеся допустили много ошибок:

— Как называются числа при сложении? (1 слагаемое, 2 слагаемое, сумма.)

— Как они между собой взаимосвязаны? (Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.)

— Как называются числа при вычитании? (Уменьшаемое, вычитаемое, разность.)

— Как они между собой взаимосвязаны? (Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое; чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.)

— Как называются числа при делении? (Делимое, делитель, частное.)

— Как они между собой взаимосвязаны? (Чтобы найти неизвестное делимое, надо частное умножить на делитель; чтобы найти неизвестный делитель, надо делимое разделить на частное.)

— Как называются числа при умножении? (1 множитель, 2 множитель, произведение.)

— Как они между собой взаимосвязаны? (Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.)

4. Какую цифру надо поставить вместо * в числах 342*, * 245, 1* 48*, * 987*, чтобы они делились: а) на 2; б) на 5; в) на 10; г) на 3; д) на 9.

5. Угадайте корень уравнения:

а) 4х + х · х = 45;             

б) 5х + х · х - 50;

в) 4х - х · х = 0;                

г) 6х - х · х = 8.

III. Сообщение темы урока

— Роджер Бэкон говорил о математике: «...дверь и ключ к науке». Без математических знаний человек не может сформироваться как гармоническая личность. Поэтому давайте продолжим с вами осваивать математику, каждый день добывая новые и новые знания, которые помогут в изучении других предметов и в нашей практической жизни.

IV. Изучение нового материала

а) Сократите дробь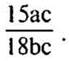 

— Числитель дроби представлен в виде произведения трех чисел 15, а и с, а знаменатель — 18, b, с.

— Назовите общий делитель числителя и знаменателя. (3 с.)

б) Сократите дроби: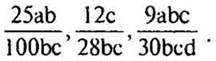 

— Назовите общий делитель числителя и знаменателя дроби.

V. Физкультминутка

VI. Закрепление изученного материала

1. — Какая дробь называется несократимой?

— Приведите примеры.

№ 243 (б) стр. 39 (один ученик работает на обратной стороне доски, а остальные самостоятельно в тетрадях, затем самопроверка).

— Дроби можно сокращать любым удобным способом.

(Ответ: .)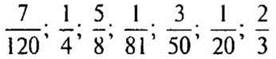

— Что называют сокращением дробей?

2. № 244 (б) стр. 40 (самостоятельно, взаимопроверка).

На доске записаны ответы.

(Ответы: .)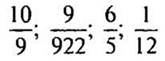

3. Выразите в часах: 1 мин; 15 мин; 25 мин; 38 мин; 4 мин; 12 мин; 30 мин.

4. № 246 стр. 40 (после краткого разбора самостоятельно, с последующей проверкой).

— Какой угол называется развернутым? (Угол, градусная мера которого равна 180°, называется развернутым.)

VII. Самостоятельная работа

Вариант I

1. Сократите дроби: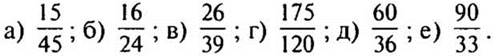 

2. Сколько десятых, пятнадцатых, двадцатых, сотых долей содержится в дроби 4/5?

Вариант II

1. Сократите дроби: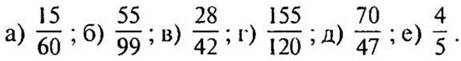 

2. Сколько десятых, пятнадцатых, двадцатых, сотых долей содержится в дроби 2/5?

VIII. Работа над задачей

1. Составьте задачу о движении по воде по краткой записи.

2. № 267 (2) стр. 42.

IX. Повторение изученного материала

1. № 255 стр. 41 (устно).

— Какие числа называются взаимно простыми?

(Ответ:

1 и 3, 1 и 10, 1 и 12, 1 и 13, 1 и 15, 1 и 16, 1 и 39,

3 и 10, 3 и 13, 3 и 16,

10 и 13, 10 и 39,

12 и 13,

13 и 15, 13 и 16,

15 и 16,

16 и 39.)

2. № 257 стр. 41 (самостоятельно).

(Ответ:

а) m = 15,

б) х = 20,

в) а = 1, b = 9; а = 9, b = 1; а = 3, b = 3;

г) х = 1, у = 14; х = 14, у = 1; х = 2, у = 7.)

3. № 249 стр. 40 (устно).

— Вспомните, как складываются и вычитаются дроби с одинаковыми знаменателями.

(Ответ: .)

X. Подведение итогов урока

— В каком случае дробь a/b будет несократимой? (Когда числа а и b будут взаимно простые.)

— Приведите примеры сократимых дробей.

Домашнее задание

№ 268 (б) стр. 42; № 271, 274 (б) стр. 43; № 264 стр. 42.

По желанию, на стр. 41 учебника прочитать исторический материал о фигурных числах.

 1.СОКРАЩЕНИЕ ДРОБЕЙ (3 ч)

Урок 25. Сокращение дробей

Цели: повторить и закрепить изученный материал; формировать навык сокращения дробей; развивать умение решать уравнения; проверить знания и навыки учащихся по изученному материалу.

Ход урока

I. Организационный момент

II. Устный счет

1. Найдите наибольший общий делитель чисел: 14 и 21; 27 и 45; 46 и 69; 28 и 12; 48 и 16; 30 и 100; 21 и 35; 12 и 60.

2. Сократите дроби: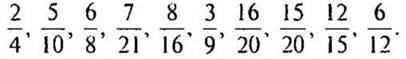 

3. Машинистка выполнила работу за 7 дней. Какую часть работы она выполнит за 1 день?

4. Туристы от базы до озера шли 4 ч со скоростью 6 км/ч. С какой скоростью они шли обратно, если обратный путь занял 3 ч? (8 км/ч.)

5. Задача-шутка. Как разделить 100 на 2 равные части, чтобы в каждой из них получилось 100? (Для этого надо провести черту дроби: 100/100.)

6. А вы знаете, откуда берет начало современное обозначение дробей? (Из Древней Индии.)

III. Индивидуальная работа

1 карточка.

I уровень

Решите уравнения относительно х.

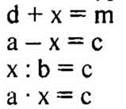
2 карточка.

II уровень

Решите уравнения относительно х.

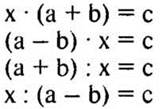
3 карточка. Повышенный уровень

Решите уравнения относительно х.

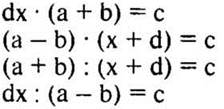
IV. Сообщение темы урока

Чтобы легче всем жилось,

Чтоб решалось, чтоб моглось.

Улыбнись, удача всем,

Чтобы не было проблем.

— Улыбнулись друг другу, создали хорошее настроение и начали работу.

— Сегодня на уроке мы продолжим сокращать дроби.

V. Повторение изученного материала

1. № 245 стр. 40 (самостоятельно, взаимопроверка, ответы — на обратной стороне доски).

2. Решите уравнения:

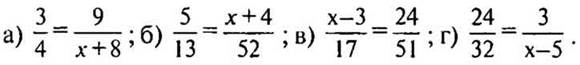
Решение:

а) — Во сколько раз числитель второй дроби больше числителя первой дроби? (В 3 раза.)

— Что тогда можно сказать о знаменателях данных дробей? (Знаменатель второй дроби тоже в 3 раза больше знаменателя первой дроби.)

— Чему равен знаменатель второй дроби? (12.)

— Запишем равенство: х + 8 = 12.

— Как называется данное равенство? (Уравнение.)

— Что неизвестно в уравнении? (Слагаемое.)

— Как найти неизвестное слагаемое? (Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.)

— Найдите корень уравнения: х = 4.

(Ответ: а) х = 4; б) х = 16; в) х = 11; г) х = 9.)

3. Сократите дроби:

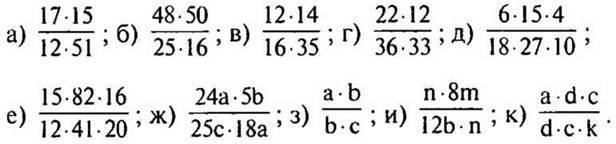
(При сокращении дробей всегда записывать над числителем и под знаменателем дроби, что остается. Писать 1 обязательно.)

4. № 248 стр. 40 (после краткого разбора самостоятельно, с последующей проверкой).

— Сколько граммов в 1 кг?

VI. Физкультминутка

VII. Работа над задачей

1. № 262 стр. 42 (после подробного разбора самостоятельно).

— Какие условия должны выполняться при составлении чисел? (Числа пятизначные, цифры четные, цифры в записи не повторяются.)

— Составьте план решения задачи.

На первом месте могут стоять любые из 4 четных цифр 2, 4, 6, 8, кроме 0, так как число не может начинаться нулем.

На втором — тоже 4 цифры, любая из 3 оставшихся и цифра 0. На третьем — любая из трех неиспользованных цифр.

На четвертом — из двух.

На пятом — только одна.

По правилу произведения получаем: 4 · 4 · 3 · 2 · 1 = 96 (чисел). (Ответ: 96 чисел.)

2. № 273 стр. 43 (после подробного разбора у доски и в тетрадях).

— Прочитайте задачу.

— Чем первый случай отличается от второго? (В первом случае 4 большие коробки и 132 карандаша, а во втором — больших коробок только 2, а карандашей 84.)

— На сколько больших коробок в первом случае больше? (На 2.)

— На сколько больше карандашей в первом случае? (132 - 84 = 48 к.)

— Сколько карандашей в трех маленьких коробках? (84 - 48 = 36 к.)

— Сколько карандашей в одной маленькой коробке? (36 : 3 = 12 к.)

Решение:

4 - 2 = 2 (к.) — больше больших коробок в первом случае.

132 - 84 = 48 (к.) — в двух больших коробках.

84 - 48 = 36 (к.) — в трех маленьких коробках.

36 : 3 = 12 (к.) — в одной маленькой коробке.

(Ответ: 12 карандашей.)

3. Решите задачу.

В классе 30 учеников, 16 из них — девочки.

Какую часть всех учеников составляют девочки?

Какую часть всех учеников составляют мальчики?

— Как узнать, какую часть одно число составляет от другого? (Надо одно число разделить на другое.)

— Мы можем сразу ответить на второй вопрос задачи? (Нет.)

— Почему? (Мы не знаем, сколько в классе мальчиков.)

— Как узнать, сколько в классе мальчиков? (Из общего количества учеников вычесть количество девочек.)

Решение:

30 - 16 = 14 (уч.) — мальчики.

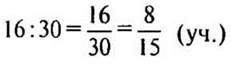 — составляют девочки.

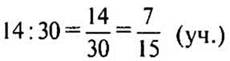 — составляют мальчики.

(Ответ: 8/15 всех учеников — девочки, 7/15 всех учеников — мальчики.)

VIII. Закрепление изученного материала

1. Найдите значение выражений:

72 - 52; 72 + 52;

(7 - 5)3; (7 + 5)2;

72 + 7; 72 - 5.

— Назовите порядок действий.

2. № 256 стр. 41 (самостоятельно, взаимопроверка).

(Ответ:   .)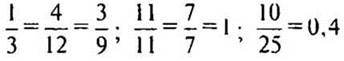

3. № 266 стр. 42 (устно).

— В результате должна получиться несократимая дробь.

(Ответ: .)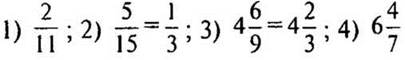

4. Устно.

Вместо * вставьте число, чтобы равенство было верным:

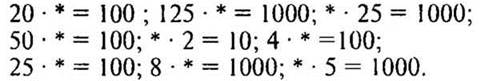
IX. Самостоятельная работа (10 мин)

Вариант I

1. Сократите дроби: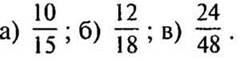 

2. Сократите: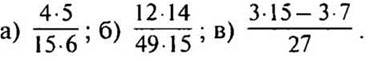 

3. Найдите наибольший общий делитель числителя и знаменателя дроби 120/300 и сократите эту дробь.

Вариант II

1. Сократите дроби: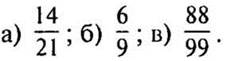 

2. Сократите: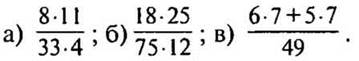 

3. Найдите наибольший общий делитель числителя и знаменателя дроби 420/756 и сократите эту дробь.

Вариант III (для более подготовленных учащихся)

1. Сократите дроби: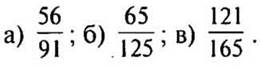 

2. Сократите: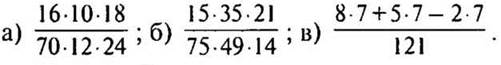 

3. Найдите наибольший общий делитель числителя и знаменателя дроби 1260/1980 и сократите эту дробь.

X. Подведение итогов урока

— Что значит сократить дробь?

— Что меняется при сокращении дробей? (Меняется только запись дроби.)

— В каком случае дробь a/b будет несократимой? (Когда числа а и b будут взаимно простые.)

Домашнее задание: № 268 (в), 269 стр. 42; № 224 стр. 37; № 272 стр. 43.

ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ (3 ч)

Информация для учителя

Обратить внимание учеников на разный смысл выражений: «общий знаменатель дробей», «наименьший общий знаменатель дробей (Н0З)».

Чтобы привести дробь к новому знаменателю, надо:

1) разделить новый знаменатель на знаменатель данной дроби, в результате получится число, которое является дополнительным множителем;

2) умножить числитель и знаменатель данной дроби на дополнительный множитель.

Чтобы найти наименьший общий знаменатель дробей, надо:

1) выяснить, не делится ли знаменатель одной дроби на знаменатель другой дроби. Если да, то больший знаменатель и будет НОЗ этих дробей;

2) выяснить, не являются ли знаменатели данных дробей взаимно простыми числами. Если да, то произведение этих знаменателей и будет НОЗ этих дробей;

3) если не выполняется ни 1, ни 2 пункт, то надо найти наименьшее общее кратное этих знаменателей. Это число и будет НОЗ этих дробей.

Чтобы привести дроби к наименьшему общему знаменателю, надо:

1) найти НОК знаменателей этих дробей. Оно и будет НОЗ;

2) найти дополнительный множитель для каждой дроби;

3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Урок 26. Приведение дробей к общему знаменателю

Цели: ввести понятие дополнительного множителя; отрабатывать умения приводить дроби к новому знаменателю и находить дополнительный множитель; закрепить знание основного свойства дроби и умение сокращать дроби; развивать математическую речь.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

1. Ознакомить учащихся с результатами самостоятельной работы.

2. Решить задания, в которых допущено наибольшее количество ошибок.

III. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 9 и 12; 12 и 16; 15 и 25; 3 и 4; 6 и 18; 4 и 15; 12 и 5; 6 и 20; 3 и 7.

2. Чему равен наибольший общий делитель двух чисел, если наименьшее общее кратное этих чисел равно их произведению? (1, так как числа взаимно простые.)

3. Восстановите запись:

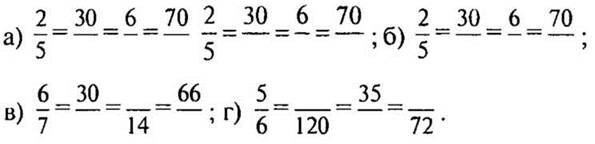
4. Объясните, почему несократимы дроби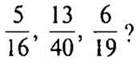 

5. На столе лежало 4 яблока, одно разрезали пополам. Сколько стало яблок? (4.)

6. Из двух пунктов, находящихся на расстоянии 144 км, навстречу друг другу выехали машина и велосипедист. Скорость машины 60 км/ч, скорость велосипедиста 12 км/ч. Через какое время они встретятся? (2 ч.)

IV. Индивидуальная работа

1 карточка

1. Сократите дроби: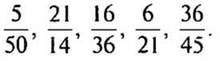 

2. Сократите: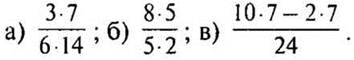 

2 карточка (для сильных учащихся)

1. Сократите дроби: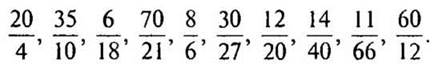 

2. Сократите: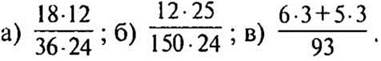 

V. Сообщение темы урока

— Сегодня на уроке мы узнаем, что такое дополнительный множитель дробей, и будем приводить дроби к новому знаменателю.

VI. Изучение нового материала

1. Подготовительная работа.

№ 286 стр. 47 (устно).

(Ответ: 2, 6, 3, 8, 4.)

— Умножьте числитель и знаменатель дроби на 6: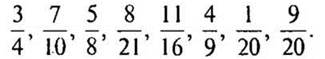 

— Какая дробь получилась в результате умножения? (В результате получается дробь, равная данной, числитель и знаменатель которой кратны прежней.)

2. Работа над новой темой.

— Дана дробь 3/4. Умножьте числитель и знаменатель дроби на 2. Какая дробь получилась? (6/8.)

— Что можно сказать о дробях 3/4 и 6/8? (3/4 = 6/8.)

— В таком случае говорят, что дробь - привели к новому знаменателю 8.

— К какому новому знаменателю можно привести данную дробь? (Дробь можно привести к любому знаменателю, кратному знаменателю данной дроби.)

Определение. Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.

VII. Закрепление изученного материала

1. № 275 стр. 45 (у доски и в тетрадях с подробным комментированием).

— Что нужно сначала найти, чтобы привести дроби к новому знаменателю? (Дополнительный множитель.)

Решение:

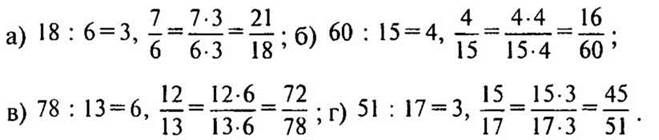
— Изменилась ли дробь после ее приведения к новому знаменателю? (Мы получили дробь, равную данной.)

— Что можете сказать о дробях 7/6 и 21/18? (Это различные записи одного и того же числа.)

2. № 276 стр. 45 (с комментированием у доски и в тетрадях).

Решение:

а) 60 : 4 · 3 = 45 мин,

60 : 4 = 15 - дополнительный множитель,

60 : 15 · 7 = 28 мин,

60 : 15 = 4 — дополнительный множитель,

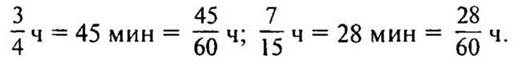
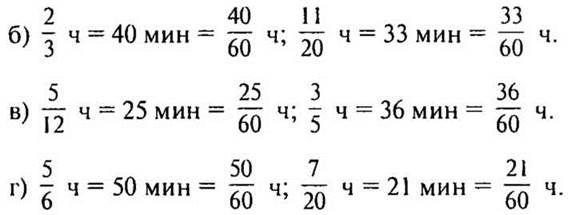
— Что интересного заметили? (Числитель новой дроби равен количеству минут.)

VIII. Физкультминутка

IX. Работа над задачей

№ 292 стр. 47 (после подробного разбора самостоятельно можно предложить решить любым способом).

— Прочитайте задачу.

— Что известно? Что надо узнать?

— Что можно узнать 1 действием? (Скорость сближения.)

— Как найти расстояние, зная скорость и время? (Скорость умножить на время.)

— Можно ли вторым действием найти расстояние? (Нет.)

— Почему? (Скорость и время выражаются разными единицами измерения.)

— В чем надо выразить 15 мин? (В секундах.)

— Сколько секунд в 1 мин? (60 с.)

— Сколько секунд в 15 мин? (15 умножить на 60.)

Решение:

34 + 46 = 80 (км/с) — скорость сближения.

15 мин = 15 · 60 = 900 (с) - до встречи.

80 · 900 = 72 000 (км)

— Как по-другому можно решить задачу?

— Что можно сделать сначала? (Перевести минуты в секунды.)

— Что можно найти потом? (Расстояния, которые пролетят комета и космический корабль за это время.)

— Что узнаем последним действием? (Все расстояние, которое будет между ними до встречи.)

Решение:

15 мин = 15 · 60 = 900 (с) — до встречи.

46 · 900 = 41 400 (км) - пролетит комета.

34 - 900 = 30 600 (км) — пролетит космический корабль.

41400 + 30 600 = 72 000 (км)

(Ответ: 72 000 км.)

X. Повторение изученного материала

1. № 288 стр. 47 (один ученик решает на обратной стороне доски, остальные — в тетрадях).

— Что значит сократить дробь?

— Какая дробь получается в результате сокращения? (Несократимая, равная данной дроби.)

Решение:

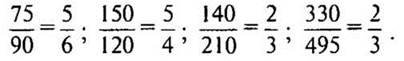
— Что интересного заметили? (При сокращении последних двух дробей получилась дробь 2/3.)

— Что можете сказать о дробях, которые надо было сокращать? (Последние две дроби равны.)

XI. Самостоятельная работа (можно выставить оценки)

Вариант I

1. № 253 стр. 40 (записать промежуточные ответы).

2. № 294 (1) стр. 47.

3. № 295 (1, 2) стр. 47.

Вариант II (для более подготовленных учеников)

1. № 284 стр. 46 (записать промежуточные ответы).

2. № 294 (2) стр. 47.

3. № 295 (3, 4) стр. 47.

XII. Подведение итогов урока

— К какому новому знаменателю можно привести данную дробь? (Дробь можно привести к любому знаменателю, кратному знаменателю данной дроби.)

— Можно ли привести дробь 2/7 к знаменателю 35? К знаменателю 25?

— Какое число называют дополнительным множителем?

— Как найти дополнительный множитель?

Домашнее задание: № 297 (а, б), 300 (а—в), 301, 303 (а) стр. 48.



ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ (3 ч)

Урок 27. Приведение дробей к общему знаменателю

Цели: формировать умения приводить дроби к наименьшему общему знаменателю и находить дополнительный множитель в более сложных случаях; формировать умения переводить обыкновенные дроби в десятичные; развивать логическое мышление.

Ход урока

I. Организационный момент

II. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 10 и 12; 12 и 8; 15 и 9; 6 и 4; 6 и 8; 12 и 15; 12 и 10; 16 и 20; 11 и 7.

2. Из одного пункта одновременно в разных направлениях вышли два туриста. Скорость первого туриста 6 км/ч, скорость второго - 7 км/ч. На каком расстоянии друг от друга они будут через 3 часа?

3. Насос наполняет бассейн за 48 мин. Какую часть бассейна насос наполнит за 1 мин?

4. В семье пять сыновей, у каждого из них одна сестра. Сколько детей в семье? (6 детей.)

III. Сообщение темы урока

— На прошлом уроке мы приводили дроби к новому знаменателю. Сегодня мы будем находить общий знаменатель для нескольких дробей и выясним, что такое наименьший общий знаменатель дробей.

IV. Изучение нового материала

1. Любые 2 дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.

— Найдите несколько общих знаменателей дробей. Назовите их наименьший общий знаменатель.

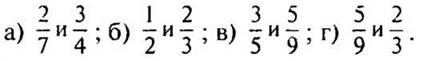
Общим знаменателем дробей может быть любое общее кратное их знаменателей.

При этом, как правило, стараются подобрать наименьший общий знаменатель (НОЗ) - тогда вычисления с дробями оказываются проще. Наименьший общий знаменатель равен наименьшему общему кратному знаменателей данных дробей.

2. Рассмотрим на примерах, как можно находить НОЗ дробей.

1) Приведем к общему знаменателю дроби 7/21 и 2/7.

— В чем особенность чисел 21 и 7? (21 делится нацело на 7.)

(Рассуждения приводит учитель.)

— Больший знаменатель — число 21 — делится на меньший знаменатель 7, следовательно, его можно взять в качестве общего знаменателя данных дробей. Этот общий знаменатель — наименьший из всех возможных.

Значит, нужно только дробь 2/7 привести к знаменателю 21. Для этого найдем дополнительный множитель: 21 : 7 = 3.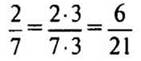 

— Какой вывод можно сделать? (Если один знаменатель дроби делится на другой, то НОЗ будет больший знаменатель.)

2) Приведем к общему знаменателю дроби 3/4 и 2/5.

— Что можете сказать о числах 4 и 5? (Числа взаимно простые.) Общий знаменатель данных дробей должен делиться и на 4, и на 5, т.е. быть их общим кратным. Общих кратных 4 и 5 бесконечно много: 20, 40, 60, 80 и т. д. Наименьшее кратное число 20 — произведение 4 и 5.

Значит, нужно привести каждую из дробей к знаменателю 20: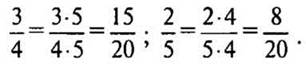 

— Какой вывод можно сделать? (Если знаменатели дробей взаимно простые числа, то наименьшим общим знаменателем будет их произведение.)

V. Физкультминутка

VI. Работа над задачей

№ 291 стр. 47 (после подробного разбора самостоятельно).

— О ком идет речь в задаче?

— Как они двигаются? (Удаляются друг от друга в разных направлениях.)

— Как узнать, на сколько изменилось между ними расстояние за 5 с? (100 - 60 = 40 см.)

— Значит, за 5 с между ними расстояние увеличилось на 40 см. Зная это, что можно найти? (Скорость удаления.)

— Как найти скорость удаления? (Расстояние разделить на время.)

— Зная скорость жука и скорость удаления, что можно узнать? (Скорость гусеницы.)

Решение:

Решите задачу двумя способами (для более подготовленных учащихся).

1 способ

1) 100 - 60 = 40 (см) — на столько расстояние между ними увеличилось за 5 с.

2) 40 : 5 = 8 (см/с) — скорость удаления.

3) 8 - 6 = 2 (см/с)

2 способ

1) 6 · 5 = 30 (см) — проползет жук за 5 с.

2) 60 + 30 = 90 (см) — на таком расстоянии находится жук от гусеницы через 5 с.

3) 100 - 90 = 10 (см) - проползет гусеница за 5 с.

4) 10 : 5 = 2 (см/с) — скорость гусеницы.

(Ответ: 2 см/с.)

VII. Закрепление изученного материала

1. № 279 стр. 45 (устно). Работа в парах.

Отвечает учителю кто-то один от пары.

— Почему дробь 3/5 нельзя привести к знаменателю 36? (36 не кратно 5.)

2. № 283 (а—е) стр. 46 (с подробным комментарием у доски и в тетрадях, а) б) записать решение подробно, затем это все проговаривать устно, записывать только дроби с новым знаменателем).

Решение:

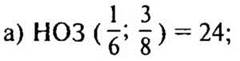
Дополнительные множители: 24 : 6 = 4, 24 : 8 = 3.

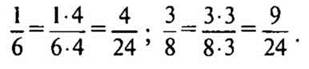
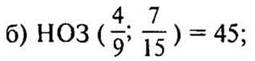
Дополнительные множители: 45 : 9 = 5, 45 : 15 = 3.

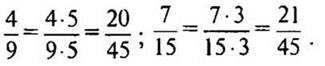
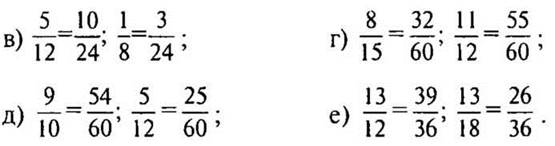
3. Назовите числа, которые:

а) больше 4/7, но меньше 5/7; б) больше 1/6, но меньше 2/6; в) больше 5/8, но меньше 3/4.

— Что нужно сделать, чтобы выполнить задание? (Привести дроби к новому знаменателю.)

4. № 281 стр. 46 (в) (один ученик на обратной стороне доски, остальные в тетрадях, самопроверка).

Решение:

VIII. Самостоятельная работа

Вариант I

1. Приведите дроби к новому знаменателю 24: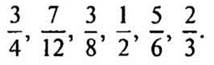 

2. Приведите дробь 3/5 к новому знаменателю: 15; 25; 40; 55; 250; 300.

3. Выразите в сотых долях дроби: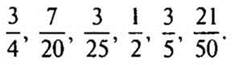 

Вариант II

1. Приведите дроби к новому знаменателю 48: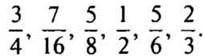 

2. Приведите дробь 4/7 к новому знаменателю: 14; 28; 49; 70; 210; 350.

3. Выразите в сотых долях дроби: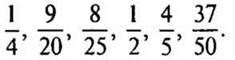 

Вариант III (для более подготовленных учащихся)

1. Приведите дроби к новому знаменателю 84: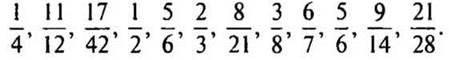 

2. Приведите дробь 5/8 к новому знаменателю: 16; 24; 56; 80; 240; 3200.

3. Выразите в сотых долях дроби: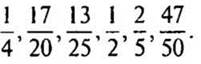 

IX. Закрепление изученного материала

1. № 290 стр. 47 (устно). Работа в парах.

— Что использовали при решении? (Основное свойство дроби.)

— Сформулируйте основное свойство дроби.

(Ответ: а) х = 3, б) х = 5, в) х = 5, г) х = 7.)

2. № 289 (в, г) стр. 47 (самостоятельно, взаимопроверка).

— Какое число называют наибольшим общим делителем числителя и знаменателя?

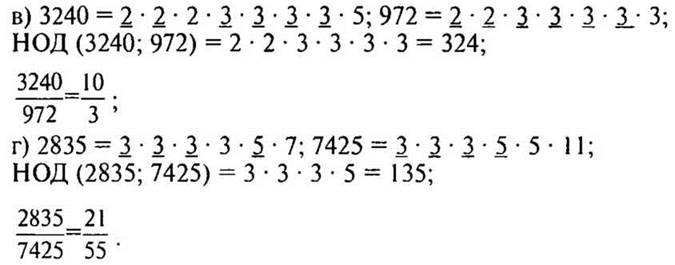
X. Подведение итогов урока

— Какое число может служить общим знаменателем двух дробей?

— Как привести дроби к наименьшему общему знаменателю?

— На каком свойстве основано правило приведения дробей к общему знаменателю?

Домашнее задание: № 297 (в, г), 300 (г-е), 302, 303 (б) стр. 48.

 ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ (3 ч)

Урок 28. Приведение дробей к общему знаменателю

Цели: повторить и закрепить изученный материал; отрабатывать навык приведения дробей к НОЗ; развивать умение решать комбинаторные задачи; проверить знания и навыки учащихся по изученному материалу.

Ход урока

I. Организационный момент

II. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 5 и 12; 12 и 18; 30 и 25; 9 и 4; 6 и 2; 4 и 24; 26 и 39; 50 и 20; 13 и 7.

2. Приведите дроби к наименьшему общему знаменателю: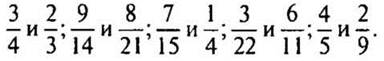 

3. Бабушка поливает огород за 15 мин. Какую часть огорода она польет за 7 мин?

4. Если в 12 ч дня идет дождь, то можно ли утверждать, что через 36 ч будет солнечная погода? (Нет, потому что будет полночь.)

5. Двое отцов и двое сыновей застрелили трех зайцев, каждый — по одному. Как это получилось? (Это были дед, отец, сын.)

III. Индивидуальная работа

Два человека работают у доски по индивидуальным карточкам, в это время с остальными учащимися проводится устная работа.

1 карточка

1. Приведите дроби к НОЗ: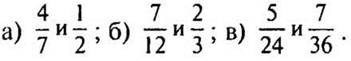 

2. Выполните действия: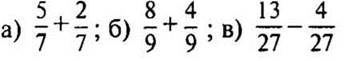 

2 карточка

1. Приведите дроби к НОЗ: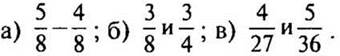 

2. Выполните действия: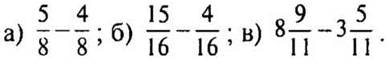 

IV. Сообщение темы урока

— Сегодня на уроке мы рассмотрим более сложные случаи нахождения НОЗ дробей.

V. Изучение нового материала

1. Подготовительная работа.

— Найдите НОК чисел 72 и 99.

— Что для этого надо сделать? (Разложить числа на простые множители.)

2. Работа над новой темой.

— Найдите НОЗ дробей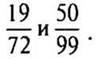 

— Что нам в этом поможет? (Разложение на простые множители знаменателей.)

— Что является НОЗ дробей? (Так как наименьшим общим знаменателем является наименьшее общее кратное, то НОЗ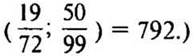 

— Как найти дополнительный множитель? (Дополнительным множителем для дроби 19/72 является число 11, а для дроби 50/99 — произведение 2 · 2 · 2 = 8, то есть те множители, которые мы не подчеркнули.)

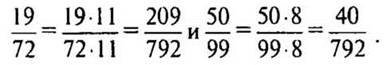
— Какой вывод можно сделать? (В более сложных случаях и дополнительные множители находят с помощью разложения на простые множители.)

VI. Физкультминутка

VII. Работа над задачей

№ 293 стр. 47 (у доски и в тетрадях с подробным комментированием).

Так как на первом месте могут стоять только 4 цифры (3, 5, 6, 8), на втором, третьем, четвертом — любая из пяти цифр, а на последнем, пятом, — только четные цифры, то есть только три (0, 6, 8), то по правилу произведения получаем: 4 · 5 · 5 · 5 · 3 = 1500 (чисел).

VIII. Закрепление изученного материала

1. № 283 (ж—м) стр. 46 (у доски и в тетрадях с подробным комментированием).

Решение:

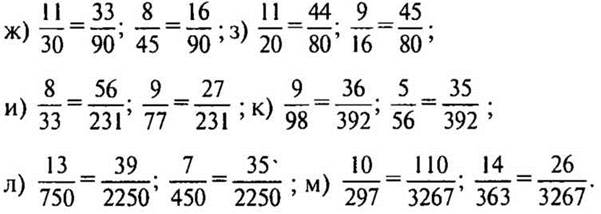
2. № 282 стр. 46 (один ученик на обратной стороне доски, остальные в тетрадях, самопроверка).

Решение:

IX. Самостоятельная работа (10 мин)

Вариант I

1. Сократите дроби: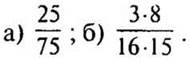 

2. Приведите дробь 3/4 к знаменателю 20, а дробь 20/72 к знаменателю 18.

3. Приведите дроби к наименьшему общему знаменателю:

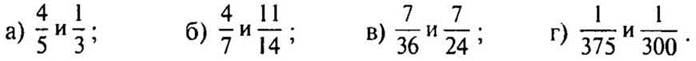
4. Приведите дроби к наименьшему общему знаменателю, предварительно сократив их: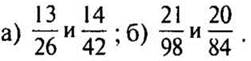 

Вариант II

1. Сократите дроби: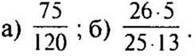 

2. Приведите дробь 4/7 к знаменателю 28, а дробь 48/108 к знаменателю 9.

3. Приведите дроби к наименьшему общему знаменателю: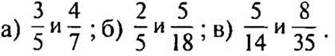 

4. Приведите дроби к наименьшему общему знаменателю, предварительно сократив их: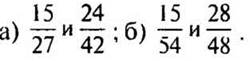 

X. Закрепление изученного материала

1. Сократите дроби: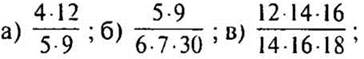 

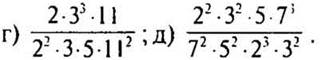
2. Какую часть метра составляет 1 см, 8 см. 40 см, 69 см, 90 см?

3. Какую часть килограмма составляет 2 г, 34 г, 50 г, 120 г, 324 г, 400 г, 650 г?

XI. Подведение итогов урока

— Наш урок подошел к концу. Скажите, что вам понравилось, а что нет?

— Какое задание вызвало наибольшее затруднение? (Выставляются оценки.)

Домашнее задание: № 298, 299, 300 (ж, з), 296 (1) стр. 48.

Урок 29. Сравнение дробей с разными знаменателями

Цели: поставить проблему по теме урока и найти выход из нее; вывести правила сравнения дробей с разными знаменателями; учить сравнивать дроби с разными знаменателями; продолжить формирование коммуникативных отношений.

Информация для учителя По ходу выполнения заданий в течение всех уроков учащиеся проговаривают правила сравнения, сокращения, сложения и вычитания обыкновенных дробей, формулируют основное свойство дроби.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний учащихся

1. Ознакомить учащихся с результатами самостоятельной работы.

2. Решить задания, где допущено наибольшее количество ошибок.

III. Устный счет

1. Назовите несколько чисел, которые имеют только три делителя. Какую закономерность можно заметить? (9, 25, 49, 81 — это квадраты натуральных чисел, сами числа являются нечетными.)

2. Сократите: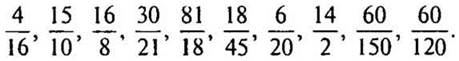 

3. Приведите дроби к наименьшему общему знаменателю: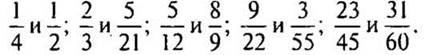 

4. Учитель проверяет все тетради за 22 мин.

Какую часть тетрадей проверит учитель за 1 мин? за 9 мин? за 16 мин?

5. Полный ящик с фруктами весит 22 кг. Ящик, заполненный наполовину, весит 12 кг. Сколько весит пустой ящик?

Решение:

1) 22 - 12 = 10 (кг) — весит половина фруктов.

2) 12 - 10 = 2 (кг).

(Ответ: 2 кг весит пустой ящик.)

IV. Индивидуальная работа

1 карточка

1. Приведите дробь 2/3 к знаменателю 9, а дробь 32/40 к знаменателю 5.

2. Приведите дроби к наименьшему общему знаменателю:

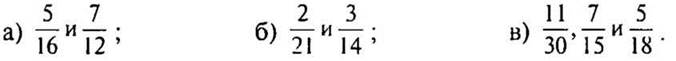
2 карточка

1. Приведите дробь 8/9 к знаменателю 18, а дробь 56/72 к знаменателю 9.

2. Приведите дроби к наименьшему общему знаменателю:

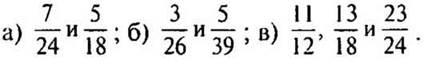
V. Сообщение темы урока

— Сегодня на уроке мы будем сравнивать дроби с разными знаменателями.

VI. Актуализация знаний учащихся

— А сейчас вспомним, как сравниваются дроби с одинаковыми знаменателями или с одинаковыми числителями.

1. Распределите числа по группам: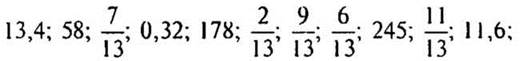 

— По какому принципу вы распределили числа?

(Ответ: на 2 группы:

целые числа: 58; 178; 245;

дробные числа: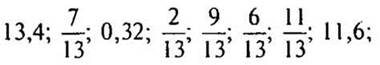 

на 3 группы:

целые числа: 58; 178; 245;

обыкновенные дроби: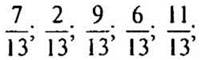 

десятичные дроби: 13,4; 0,32; 11,6.)

— Расположите данные дроби в порядке возрастания.

— А как вы узнали, что дроби надо было так расположить?

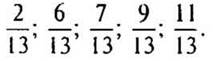
(Ответ: 2/13 — самая маленькая дробь, 11/13 — самая большая дробь).

— Какое правило сравнения дробей использовали? (Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

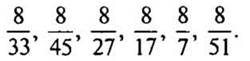
2. Запишите дроби в порядке убывания:

— Что значит записать дроби в порядке убывания? (От наибольшего числа к наименьшему числу.)

— Как сравнивать дроби с одинаковыми числителями? (Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.)

Решение:

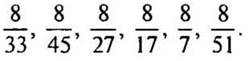
VII. Изучение нового материала

1. Подготовительная работа.

—  А теперь предлагаю вам сравнить дроби. Рассмотрите их.

— Что вы заметили? (Знаменатели и числители у дробей разные.)

— Найдите среди этих дробей самую маленькую и самую большую.

— Появилось много мнений. У нас возникла проблема: как сравнить дроби с разными знаменателями?

— Чтобы ответить на вопрос, мы проведем исследовательскую работу. Работать будем в группах по инструкции.

(Инструкцию записать на доске.)

Инструкция:

1. Внимательно рассмотрите числа.

2. Расположите эти дроби на координатном луче, самостоятельно выберите единичный отрезок.

3. Сравните полученные отрезки. Сделайте вывод.

4. Расположите дроби в порядке возрастания. Выделите наименьшую дробь зеленным цветом, а наибольшую - красным.

5. Постарайтесь сформулировать вывод: как сравнить дроби с разными знаменателями.

— Скажите, удобно ли каждый раз, сравнивая дроби, отмечать их на координатном луче?

— Как же сравнивать такие дроби?

— Сформулируйте правило сравнения дробей с разными знаменателями и числителями.

2. Работа над новой темой.

— Сравните дроби 2/3 и 3/5.

— Приведем дроби к наименьшему общему знаменателю. (Так как 3 и 5 взаимно простые числа, то НОЗ дробей будет их произведение.)

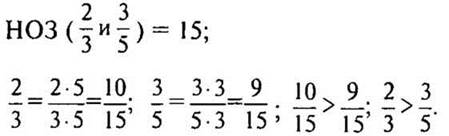
3. Учебник, стр. 50 (в некоторых учебниках опечатка — вместо слова «дательном» должно быть написано «родительном»).

— Прочитайте текст под рубрикой «Говори правильно».

— Прочитайте двумя способами данные записи: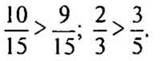 

(Десять пятнадцатых больше девяти пятнадцатых или дробь десять пятнадцатых больше дроби девять пятнадцатых.)

VIII. Физкультминутка

IX. Закрепление изученного материала

1. № 304 (а, б) стр. 50 (у доски объясняет сильный ученик, остальные — в тетрадях).

— Как сравнивать дроби с разными знаменателями?

Решение:

а) Сравним дроби 2/3 и 8/21.

— Приведем дроби к наименьшему общему знаменателю. (Так как 21 делится на 3, то НОЗ дробей будет больший знаменатель 21.)

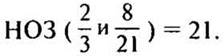
— Как сравнивать дроби с одинаковыми знаменателями? (Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

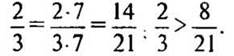
б) Сравним дроби 4/15 и 2/5.

— Приведем дроби к наименьшему общему знаменателю. (Так как 15 делится на 5, то НОЗ дробей будет больший знаменатель 15.)

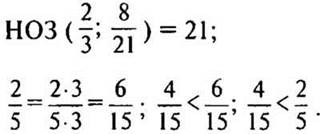
2. № 305 стр. 50 (решение записывать короче, все объяснение проговаривать).

Решение:

 (Ответ: а) 1/30; б) 9/14.)

X. Самостоятельная работа

Взаимопроверка. Ответы на доске.

Вариант I. № 311 (а, б) стр. 51, № 352 (а) стр. 56.

Вариант II. № 311 (в, г) стр. 51, № 352 (б) стр. 56.

XI. Работа над задачей

I. № 313 стр. 51 (у доски и в тетрадях).

— Прочитайте задачу.

— Что нужно сделать, чтобы ответить на вопрос задачи? (Сравнить дроби.)

Решение:

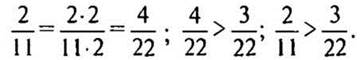
(Ответ: рисунки занимают больше места в книге.)

2. № 315 стр. 51 (у доски и в тетрадях).

— Что известно в задаче?

— Что надо узнать?

— Что примем за единицу? (Всю работу.)

Решение:

Пусть 1 — вся работа.

Какую часть бассейна заполняет узкая труба за 1 ч? 1/10 (часть).

Какую часть бассейна заполняет широкая труба за 1 ч? 1/4 (часть).

Какую часть бассейна заполняет узкая труба за 7 ч? 7/10 (бассейна).

Какую часть бассейна заполняет широкая труба за 3 ч? 3/4 (бассейна).

Какая труба дает меньше воды?

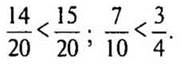
(Ответ: узкая труба.)

3. № 355 стр. 56 (после разбора самостоятельно).

— К какому виду задач можно отнести данную задачу? (К комбинаторным.)

— Первым уроком какой урок может быть? (Любой из пяти.)

— Вторым уроком какой урок может быть? (Любой из оставшихся четырех.)

— Третьим уроком какой урок может быть? (Любой из оставшихся трех.)

— Четвертым уроком какой урок может быть? (Любой из оставшихся двух.)

— Пятым уроком какой урок может быть? (Только какой-то один урок.)

— Какое правило будем использовать при решении задачи? (Правило произведения.)

Решение:

5 · 4 · 3 · 2 · 1 = 120 (вариантов).

(Ответ: 120 вариантов.)

XII. Повторение изученного материала

№ 281 (б) стр. 46 (устно с подробным комментированием).

Решение:

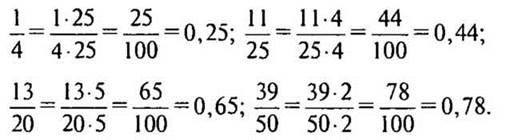
XIII. Подведение итогов урока

— Как сравнивать дроби с одинаковыми знаменателями?

— Как сравнивать дроби с одинаковыми числителями?

— Как сравнивать дроби с разными знаменателями?

Домашнее задание

Учебник, стр. 50 (прочитать текст под рубрикой «Говори правильно»). № 359 (а-г), 361 стр. 57; № 370 стр. 58.



Скачано с www.znanio.ru