математика

Конспект урока математики в 6 классе

Тема: Взаимное расположение графиков линейных функций

Цели урока:

1) образовательные: научиться определять взаимное расположение графиков линейных функций в зависимости от значений коэффициентов k и b;

2) развивающие: способствовать формированию умений применять приемы: обобщения, сравнения, выделение главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти;

3) воспитательные: воспитывать чувство товарищества, взаимовыручки, ответственности, трудолюбие и аккуратность.

Тип урока: урок усвоения новых знаний учащимися.

Формы организации учащихся: фронтальная, парная, групповая, индивидуальная.

Методы обучения: частично-поисковый, интерактивные методы.

Используемые технологии: ИКТ, проблемное обучение.

Оборудование: компьютерный класс, презентация, карточки с заданиями.

Программное обеспечение: компьютерная программа My TestX.

ХОД УРОКА

1. Организационный момент.  Приветствие учащихся.

Девизом нашего урока возьмем высказывание французского математика, философа Рене Декарта: «Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать».

2. Актуализация знаний. Устная фронтальная работа.

а) «Лови ошибку»:

1) Линейной называется функция вида , где k и  b- некоторые числа.

2) Переменная х в формуле линейной функции является зависимой переменой, а  у – независимой переменной.

3) Для построения графика линейной функции достаточно взять одну точку.

4) Графиком линейной функции у=b  является прямая, параллельная оси ОУ.

5) Точка А(0;3) принадлежит графику функции у=3х+2.

6) Областью определения функции у =2х+1 является промежуток (0; +).

б) Мы знаем, что графиком линейной функции является прямая. Как могут располагаться две прямые на плоскости? (Две прямые могут быть параллельными, могут пересекаться и совпадать). Ребята, мы с вами научились по формуле вычислять значения переменных  х и у, определять принадлежность точки графику функции.

Проблемный вопрос: Можем ли мы определить взаимное расположение графиков линейных функций, не выполняя построения графиков?

3. Постановка темы и целей урока.

Ребята, давайте определим тему урока. Откройте тетради, запишите тему урока: «Взаимное расположение графиков линейных функций».  Сформулируйте цели урока: определить от чего зависит взаимное расположение графиков линейных функций.

4. Усвоение новых знаний. Работа в парах. Каждой паре дается карточка с заданием.

Карточка 1. Постройте в одной системе координат графики функций  у = 0,5х - 1,5;   

  у = 0,5х - 0,5 ; у = 0,5х - 3.

Ответьте на вопросы:

1) Каково взаимное расположение графиков функций?

3) Каковы координаты точек пересечения каждого графика с осями координат?

Карточка 2. Постройте в одной системе координат графики функций: у = 3х+2;

 у = 0,8х+2;  у  = - х +2.

Ответьте на вопросы:

1) Каково взаимное расположение графиков функций?

2) Каковы координаты точек пересечения каждого графика с осями координат.

Карточка 3. Постройте в одной системе координат графики функций у = 3х - 1; у = -2х+2, у = 0,5х+4.

Ответьте на вопросы:

1) Каково взаимное расположение графиков функций?

2) Каковы координаты точек пересечения каждого графика с осями координат?

После выполнения задания осуществляется проверка с помощью интерактивной доски.

От чего зависит взаимное расположение графиков линейных функций? Учащиеся самостоятельно делают выводы:

1)Если числа k в формулах линейных функций равны, то графики параллельны.

2) Если числа k в формулах линейных функций различны, то графики пересекаются.

3)Если в формулах линейных функций числа k различны, а совпадают числа b, то графики пересекаются в точке (0; b) на оси ординат.

А в каком случае графики линейных функций будут совпадать? Учащиеся приходят к выводу, что должна быть равны числа k и b.

Давайте, обратим особое внимание на тот факт, что ордината точки пересечения графика линейной функции с осью ОУ равна значению b.

5. Первичное осмысление и применение полученных знаний. Устная фронтальная работа с классом.

Задание 1. Не выполняя построения, установите взаимное расположение графиков линейных функций:

1. у = 4х  и у = 4х – 4;

2. у = х +2  и у = -2х – 1;

3. у =3х + 6  и у = 3х + 6;

4. у =10х – 5  и у = 3х – 5;

5. у =0,5 х + 7  и у =  х – 7;

6. у =2х + 8  и у = 3х + 5;

7. у = 16х – 9  и у = 16х +5.

Задание 2. Для каждой линейной функции назовите коэффициент k и ординату точки пересечения графика функции с осью ОУ:

у = 0,25х+19; у = 2х-3; у = 0,2х; у = -х-1; у = 18-х.

Задание 3. Задайте линейную функцию, если  k = - 2 и точка пересечения с осью ОУ: А(0;3),  и k =5 и А(0;-10) .

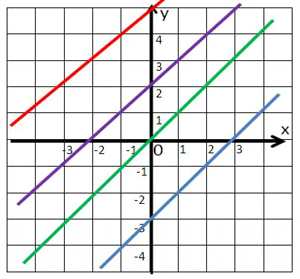
Задание 4. Составить формулы для функций, изображенных графиками:

6. Закрепление изученного материала. Работа в тетрадях.

Задание 1. Составьте уравнение линейной функции, график которой параллелен графику функции у = - 4х + 2,5 и пересекает график функции у = -2х – 3 в точке на оси ординат.

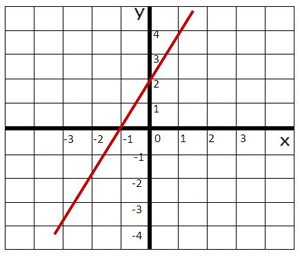
Задание 2. Составьте  функцию для графика, изображенного на рисунке:

7. Проверка и контроль знаний.  Работа в группах.

1) «Исправь ошибку»:

а) прямые у = 7х - 4 и у = 7х +5 – параллельны;

б) прямые у = 10х -3 и у = - 10х -6 – параллельны;

в) прямые у = 0,3х -2 и у = 8,1х -2 – пересекаются;

г) прямые у = - 7х +3 и у = -7х -2 – пересекаются;

д) прямые у = 3х +2 и у = 3х  – параллельны;

е) прямые у = -2,3х  и у = 2,3х  – пересекаются.

2) «Домино». Каждая группа получает два вида карточек (карточки-вопросы и карточки ответы), на которых записаны формулы линейных функций. Нужно установить соответствие между теми функциями, графики которых параллельны.

Карточки вопросы: у = 2х+3;  у = - 0,5х; у = -х-2,5; у =1,4+0,6х; у = -19-37х; у =х+1,8; у=16+х.

Карточки-ответы: у = - 37х+12; у = 0,5х; у = 7-х; у = 1,4-0,9х; у=0,2х-3; у = х+1,8;

   у = 16-х;  у = 5+2х; у = 5х+1,4.

Каково взаимное расположение графиков линейных функций на двух оставшихся карточках? (Они пересекаются в точке (0;1,4)

3) Компьютерное тестирование.

1) Не выполняя построения, определите взаимное расположение графиков у = 3х-1 и 

    у = 3х+5.

    А) пересекаются;   В) параллельны;   С) совпадают.

2) Не выполняя построения, определите взаимное расположение графиков у = 7х-3 и 

    у = 3х-7.

    А) пересекаются;   В) параллельны;   С) совпадают.

3) Не выполняя построения, определите взаимное расположение графиков у = 0,5х +  и 

    у = 0,75+х.

   А) пересекаются;   В) параллельны;   С) совпадают.

4) График какой из перечисленных линейных функций параллелен графику функции 

   у = - 15х – 7?

   А) у = 15х - 7.   В) у = -7х - 15.  С) у = -15х + 7. 

5)Дана функция, графиком которой является прямая, параллельная оси абсцисс и проходящая через точку А(5;-3):

   А) у = 5   В) у = -3     С) у = -3х+5   Д) у = 5х – 3.

6) Не выполняя построений и вычислений, определите, графики каких функций изображены на рисунке

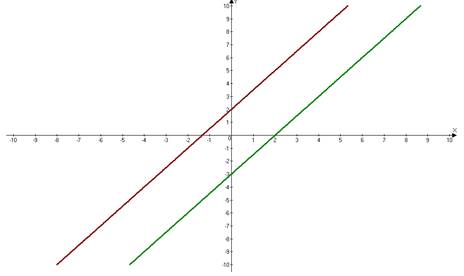
 А)   (a) у = 2х- 3;  (b)  у = 1,5х +2.

 В)   (a) у = 1,5х – 3;  (b)  у = 1,5х + 2.

 С)   (a) у = 1,5х +2;  (b)  у = 1,5х – 3.             

 Д)   (a) у =  1,5х – 2; (b)  у = 2х + 3.

7) График какой линейной функции пересекается с графиком функции у= 27х – 32 в точке (0; - 32)?

    А)  у = 16х – 32.      В) у = 32х – 27.     С) у = 27х + 32.

8. Домашнее задание.

   1) Прочитать §51 , решить №1221, №1231.

   2) Творческое задание: придумать сказку по теме урока.

9. Итоги урока и объявление оценок.  Давайте подведем итоги, что мы можем сказать про расположение графиков линейных функций относительно друг друга?

- Графики параллельны, если коэффициенты при  х одинаковые:  k₁ = k₂, а числа b₁ и b₂ разные.

- Графики пересекаются, если коэффициенты при  х различны:  k₁  ≠ k₂

- Графики совпадают, если  коэффициенты при х равны:  k₁ = k₂ и b₁ и b₂ одинаковые

10. Рефлексия.  Выберите одну фразу для соседа по парте:

-Ты молодец.

-Я доволен твоей работой на уроке.

-Ты мог бы поработать лучше.