Пояснительная записка

1.1 Нормативная база

Рабочая программа по  алгебре в 7 классе составлена в соответствии с документами:

- Приказ Минобразования РФ от 5 марта 2004 года №1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»;

- Учебный план МБОУ Гагинская СОШ на 2014- 2015 учебный год;

- Примерной программы основного общего образо­вания по математике (Сборник нормативных документов. Математика. М: Дрофа, 2004).

 

1.2 Учебно – методическое обеспечение

1.   Мордкович А.Г. «Алгебра-7» часть 1 , учебник – М.: Мнемозина, 2009

2.   Мордкович А.Г. «Алгебра-7» часть 2, задачник – М.: Мнемозина, 2009

3.   Александрова Л.А. «Контрольные работы. Алгебра -7» - М.: Мнемозина, 2009

4.   Александрова Л.А. «Самостоятельные работы. Алгебра -7» - М.: Мнемозина, 2009

  Дополнительная литература:

1. «Нестандартные задания по математике 5 – 11 классы», В.В. Кривоногов.

2. «Математика, итоговые уроки 5-9 классы», О.В. Бощенко.

3. «Математические олимпиады в школе 5-11 классы», А.В. Фарков.

4. Тесты по математике 5-11 классы, М.А. Максимовская и др.

5. «Учитесь мыслить нестандартно», Б.М. Абдрашитов и др.

6. «Интеллектуальные турниры, марафоны, бои», библиотека «Первого сентября», 2003 г.

7.  «Тесты для промежуточной аттестации 7-8 классы», Ф.Ф. Лысенко, 2007 г.

8. «Я иду на урок математики, 7 класс, алгебра», библиотека «Первого сентября», 2001 г.

Список литературы для ученика

1.                 Мордкович А.Г. «Алгебра-7» часть 1 , учебник – М.: Мнемозина, 2009

2.                 Мордкович А.Г. «Алгебра-7» часть 2, задачник – М.: Мнемозина, 2009

3.                 Звавич «Дидактичеаские материалы по алгебре, 7 класс»

 

1.3 Цели курса

Изучение алгебры в 7 классе направлено на достижение цели:

ü        овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

ü      интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

ü      формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

 

1.4Задачи курса

Обучения: овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования; интеллектуальное развитие; получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культурыформирование

Развития:  ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей; математической речи; сенсорной сферы; двигательной моторики; внимания;  памяти; навыков  само и взаимопроверки.

Воспитания:  культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики   для научно-технического прогресса; волевых качеств; коммуникабельности; ответственности.

Валеологические: сохранение и укрепление здоровья детей; наблюдение за посадкой детей; активное внедрение здоровьесберегающих  технологий.

1.5 Обоснование разбивки содержания программы на отдельные темы, выделения на данные темы учебных часов.

   Рабочая программа составлена для учащихся 7 «б» класса МБОУ Гагинская СОШ, рассчитана на 105 часов в год,  3 часа в неделю. Предусмотрено 8 тематических контрольных работ, 1 полугодовая и 1 итоговая; самостоятельные или проверочные работы после изученной темы.

 

 Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей ре­альности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. В ходе освоения содержания курса учащиеся получают возможность:

ü       сформировать практические навыки выполнения уст­ных, письменных, инструментальных вычислений, развить вычис­лительную культуру;

ü  овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

ü  изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

ü  развить логическое мышление и речь — умения логически обосно­вывать суждения, проводить несложные систематизации, приво­дить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллю­страции, интерпретации, аргументации и доказательства;

ü  сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реаль­ных процессов и явлений.

В ходе преподавания алгебры в 7 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

ü  планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

ü  решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

ü  исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

ü  ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

ü  проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

ü  поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

 

 В программе используются педагогические технологии: технологии на основе активизации и интенсификации деятельности учащихся (игровые технологии); технологии на основе активизации и интенсификации деятельности учащихся (системы развивающего обучения с направленностью на развитие творческих качеств личности); технологии на основе эффективности управления и организации учебного процесса (технология уровневой дифференциации обучения на основе обязательных результатов).

Методы :

ü  методы организации и осуществления учебно-познавательной деятельности:  словесный (диалог, рассказ и др.);      наглядный (опорные схемы, слайды  и др.); практический (упражнения, практические работы, решение задач,моделирование и др.); исследовательский; самостоятельной работы; работы под руководством преподавателя; дидактическая игра;

ü  методы стимулирования и мотивации: интереса к учению;  долга и ответственности в учении;

ü  методы контроля и самоконтроля в обучении: фронтальная устная проверка, индивидуальный устный опрос, письменный контроль (контрольные и практические работы, тестирование, письменный зачет, тесты).

Формы текущего и итогового контроля: самостоятельная работа, тестирование, теоретические диктанты, контрольные работы.

 

Тематическое планирование учебного материала

№	Тема	Количество часов	Количество к/работ
1	Математический язык. Математическая модель.	12	1
2	Линейная функция	14	1
3	Система двух линейных уравнений с двумя переменными	12	1
4	Степень с натуральным показателем	7	1
5	Одночлены. Операции над одночленами	8	1
6	Многочлены. Арифметические операции над многочленами	17	1
7	Разложение многочленов на множители	20	1
8	Функция у = х2	7	1
9	Итоговое повторение	7	1

 

 

2. Содержание программы учебного курса

 

1.     Математический язык. Математическая модель (12 часов)

Числовые и алгебраические выражения.  Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.

Основная цель изучения данной темы – выработать у учащихся умение выполнять действия над степенями с натуральным показателем.

2.     Линейная функция (14 часов)

Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М(а;b) в прямоугольной системе координат.

Линейное уравнение с двумя переменными. Решение уравнение. График уравнения. Алгоритм построения графика уравнения.

Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Взаимное расположение графиков линейных функций.

3.     Системы двух линейных уравнений с двумя переменными (12 часов)

Система уравнений. Решение системы уравнений. Графический способ решения уравнений. Метод подстановки. Метод алгебраического сложения.

Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи)

4.     Степень с натуральным показателем (7 часов)

Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.

5 . Одночлены. Операции над одночленами (8 часов)

Понятие одночлена. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Арифметические операции над одночленами.

6.     Многочлены. Арифметические операции над многочленами (17 часов)

Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных слагаемых членов многочлена. Стандартный вид многочлена.

Формулы сокращенного умножения. Деление многочлена на одночлен.

7.     Разложение многочленов на множители (20 часов)

Разложение многочлена на множители: с помощью формул сокращенного умножения, способ группировки, вынесение общего множителя за скобки, комбинированный способ. Метод выделения полного квадрата.

Основная цель изучения данной темы - выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочлена на множители.

Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений.

Понятие алгебраической дроби. Сокращение алгебраической дроби.

Тождество. Тождественно равные выражения. Тождественные преобразования.

8.     Квадратичная функция (7 часов)

Квадратичная функция, ее свойства и график. Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Функциональная символика.

9.     Итоговое повторение (7 часов).

3. Требования к уровню подготовки учащихся

       В результате изучения курса алгебры, обучающиеся должны знать:

ü  математический язык;

ü    свойства степени с натуральным показателем;

ü   определение одночлена и многочлена, операции над одночленами и многочленами; формулы сокращенного              умножения; способы разложения на множители;

ü    линейную функцию, её свойства и график;

ü    квадратичную функцию и её график;

ü     способы решения системы двух линейных уравнений с двумя переменными;

        должны уметь:

ü    составлять математическую модель при решении задач;

ü    выполнять действия над степенями с натуральными показателями, показателем, не равным нулю,  используя       свойства степеней;

ü    выполнять арифметические операции над одночленами и многочленами, раскладывать многочлены на   множители, используя метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения;

ü    строить графики линейной и квадратичной функций;

ü     решать системы двух линейных уравнений с двумя переменными;

ü     проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;

ü     извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;

ü    решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения.

Обладать базовыми компетенциями: использовать приобретенные знания и умения в практической деятельности и повседневнойжизни для: для построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин; для выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; интерпретация графиков реальных зависимостей между величинами; для совершенствования навыков по использованию справочного материала и простейших вычислительных устройств.

Обладать ключевыми компетенциями:

ü   Информационно-технологическими: уметь при помощи реальных объектов и информационных технологий самостоятельно искать, отбирать, анализировать и сохранять информацию по заданной теме, интегрировать её в личный опыт; уметь представлять материал с помощью творческих работ, рефератов, средств презентации; уметь задавать и отвечать на вопросы по изучаемым темам с пониманием и по существу.

ü   Коммуникативными: уметь работать в группе: слушать и слышать других, считаться с чужим мнением и аргументировано отстаивать своё, организовывать совместную работу на основе взаимопомощи и уважения; уметь обмениваться информацией по темам; проводить доказательные рассуждения, логическое обоснование выводов, уметь различать доказанные и недоказанные утверждения; развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.

ü   Учебно-познавательными: уметь планировать учебную деятельность: самостоятельно и мотивированно организовывать свою познавательную деятельность – ставить цель, определять задачи для её достижения; совершенствовать навыки организации учебной деятельности: организация рабочего места, режима работы; развивать навыки мыслительной деятельности: умение выделять главное, анализ и синтез, классификация, обобщение, логическое построение ответа, речи, формулирование выводов, решение задач; создать основу для осмысливания своих действий: организация само- и взаимоконтроля, рефлексивный анализ.

 Обладать специальными компетенциями:

ü   умениями и навыками построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;

ü   навыками выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения   расчётов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента.

Решать следующие жизненно-практические задачи:

ü самостоятельно приобретать и применять знания в различных ситуациях;

ü   работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других;

ü извлекать учебную информацию на основе сопоставительного анализа объектов;

ü пользоваться предметным указателем, энциклопедией и справочником для нахождения информации;

ü самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем;

ü выстраивания аргументации при доказательстве;

ü распознавания логически некорректных рассуждений.

4.Критерии оценивания достижений учащихся

  1. Оценка письменных контрольных работ обучающихся по математике.

  Ответ оценивается отметкой «5», если:

·        работа выполнена полностью;

·        в логических рассуждениях и обосновании решения нет пробелов и ошибок;

·       в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или                   непонимания учебного материала).

Отметка «4» ставится в следующих случаях:                                                                     

·        работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось              специальным объектом проверки);

·        допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

·          допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

·   допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

·     работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

     Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике.

Ответ оценивается отметкой «5», если ученик:

·        полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

·     изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

·        правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

·       показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

·     продемонстрировал знание теории ранее изученных сопутствующих тем,  сформированность и устойчивость используемых при ответе умений и навыков;

·        отвечал самостоятельно, без наводящих вопросов учителя;

·       возможны одна – две  неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

·        в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

·        допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

·        допущены ошибка или более двух недочетов  при освещении второстепенных вопросов или в выкладках,  легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

·          неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

·          имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

·       ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

·        при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

·        не раскрыто основное содержание учебного материала;

·        обнаружено незнание учеником большей или наиболее важной части учебного материала;

·        допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

·          ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

 

3. Общая классификация ошибок.

                        При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

-           незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов   обозначений величин, единиц их измерения;

-         незнание наименований единиц измерения;

-         неумение выделить в ответе главное;

-         неумение применять знания, алгоритмы для решения задач;

-         неумение делать выводы и обобщения;

-         неумение читать и строить графики;

-         неумение пользоваться первоисточниками, учебником и справочниками;

-         потеря корня или сохранение постороннего корня;

-         отбрасывание без объяснений одного из них;

-         равнозначные им ошибки;

-         вычислительные ошибки, если они не являются опиской;

-          логические ошибки.

3.2. К негрубым ошибкам следует отнести:

-           неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

-           неточность графика;

-           нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

-           нерациональные методы работы со справочной и другой литературой;

-           неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

-         нерациональные приемы вычислений и преобразований;

-         небрежное выполнение записей, чертежей, схем, графиков.

 

 

 

 

6. Информационное сопровождение, цифровые и электронные образовательные ресурсы

 

 

1.   http://uchitmatematika. ucos. ru/

2.   http:// mikhatoval. edum. ru/

3.   http://yroki. net

4.   http:// rusedi.ru/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контрольно- измерительные материалы

Перечень обязательных контрольных работ:

Контрольная работа №1: «Выражения, преобразования выражений, тождества»

Контрольная работа №2: «Линейные уравнения с одной переменной».

Контрольная работа №3: «Линейная функция»

Контрольная работа №4: «Степень с натуральным показателем».

Контрольная работа №5: «Многочлен».

Контрольная работа №6: «Умножение многочленов. Способ группировки».

Контрольная работа №7:  «Разложение многочлена на множители».

Контрольная работа №8: «Системы линейных уравнений с двумя переменными».

Итоговая контрольная работа.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контрольная работа № 1

Вариант 1

1^о. Найдите значение алгебраического выражения   4(4с – 3) + 8(5 – 2с) – (10с + 8)           при с = 0,12

2^о. Решите уравнение:  а) 2х + 3 = 0;            б) 6х – 7 = 15 + 2х

3^о. Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Луч с началом в точке (-5). Сколько отрицательных чисел принадлежит данному промежутку?

4^о.  Постройте прямую, проходящую через данные точки, и запишите ее аналитическую модель:  А(-3; 1);   В(-3; 4)

5.  Решите задачу:

В книге 190 страниц. В пятницу Знайка прочитал в 1,2 раза меньше страниц, чем в субботу, а в субботу на 20 страниц меньше, чем в воскресенье. Сколько страниц он прочитал в субботу?

 

Контрольная работа № 1

Вариант 2

1. Найдите значение алгебраического выражения  2(12с – 7) + 6(5 – 4с) – 3(2с + 5)           при с =

2^о. Решите уравнение: а) 3х - 2 = 0;            б) 7х + 1,5 = 10х - 3

3^о. Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Открытый луч с концом в точке 7. Сколько натуральных чисел принадлежит данному промежутку?

4^о.  Постройте прямую, проходящую через данные точки, и запишите ее аналитическую модель: А(-2; 3);   В(1; 3)

5.  Решите задачу:

Капитан Врунгель загрузил на свой корабль в трех ящиках 44 кг бананов. В первом ящике было в 1,5 раза больше бананов, чем во втором, и на 4 кг меньше, чем в третьем. Сколько килограммов бананов в первом ящике?

 

Контрольная работа № 2

Вариант 1

1.      а) Найдите координаты точек пересечения графика линейного уравнения

           – 3х + 2у – 6 = 0 с координатными осями и постройте его график.

б) Принадлежит ли графику данного уравнения точка К?

2.      а) Преобразуйте линейное уравнение с двумя переменными 2х + у – 1 = 0 к виду линейной функции и постройте ее график.

б) Найдите наименьшее и наибольшее значение этой функции на отрезке [-1;2].

3.      Найдите координаты точки пересечения прямых у = 3 – х и у = 2х.

4.      а)  Задайте прямую пропорциональность формулой, если известно, что ее график параллелен графику линейной функции у = 3х – 4.

б)  Определите, возрастает или убывает заданная функция. Ответ объясните.

5.      При каком значении р решением уравнения 5х + ру – 3р = 0 является пара чисел (1;1) ?

 

 

Контрольная работа № 2

Вариант 2

1.      а) Найдите координаты точек пересечения графика линейного уравнения

           2х - 5у – 10 = 0 с координатными осями и постройте его график.

б) Принадлежит ли графику данного уравнения точка М?

2.      а) Преобразуйте линейное уравнение с двумя переменными   -2х + у + 3 = 0 к виду линейной функции и постройте ее график.

б) Найдите наименьшее и наибольшее значение этой функции на отрезке [-2;1].

3.      Найдите координаты точки пересечения прямых у =  – х и у = 2х - 3.

4.      а)  Задайте прямую пропорциональность формулой, если известно, что ее график параллелен графику линейной функции у = -4х + 7.

б)  Определите, возрастает или убывает заданная функция. Ответ объясните.

5.      При каком значении р решением уравнения -рх + 2у + р = 0 является пара чисел (-1;2) ?

 

Контрольная работа № 3

Вариант 1

1^о. Решите методом подстановки систему уравнений                      3х – у = -5,

                                                                                                               -5х + 2у = 1.

2^о. Решите методом алгебраического сложения систему уравнений                          9х + 4у = 8,

                                                                                                                                            5х + 2у = 3.

3^о. Решите графически систему уравнений                  х + у = 5,

                                                                                           у = 2х + 2.

4.В туристический поход ребята взяли двухместные и трехместные палатки. Сколько человек разместилось в трехместных палатках, если на 26 человек взяли 10 палаток?.

5.  Дана система уравнений              ах + by  = 36,

ax - by = 8.

     Пара чисел (2;-1) является ее решением. Найти значения a  и b.

 

 

 

 

 

 

 

 

Контрольная работа № 3

Вариант 2

 

1^о. Решите методом подстановки систему уравнений                       4х – 9у = 3,

                                                                                                                 х + 3у = 6.

2^о. Решите методом алгебраического сложения систему уравнений                          6х - 7у = -2,

                                                                                                                                            2 х – 5у = 2.

3^о. Решите графически систему уравнений                  у = 2х - 1,

                                                                                          х + у  = -4.

4.В копилку складывали двухрублевые и пятирублевые монеты. Когда копилку вскрыли, в ней оказалось пятирублевых монет на 12 меньше, чем двухрублевых, а всего денег на сумму 178 руб. Сколько рублей пятирублевыми монетами было в копилке?

5.  Дана система уравнений              ах – by  = -24,

ax + by  = 4.

     Пара чисел (1;-2) является ее решением. Найти значения a  и b.

 

Контрольная работа № 4

Вариант 1

1^о. Упростить выражение:         а)              б)             в)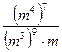 

2.      Вычислите:  

3.      Сравните значения выражений   и  1,6^о

4.      Объем куба равен 27 см³. Найти длину ребра куба и площадь полной поверхности куба.

5.      Решите уравнение       10^х = 10000000

 

 

 

 

 

 

 

 

Контрольная работа № 4

Вариант 2

 

1^о. Упростить выражение:         а)              б)             в)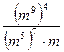 

2.      Вычислите:  

3.      Сравните значения выражений   и  (-2)^о

4.      Площадь поверхности  куба равен 24 см². Найти длину ребра куба и объем куба.

5.      Решите уравнение       2^х = 512

 

Контрольная работа № 5

Вариант 1

1.      Приведите одночлен к стандартному виду и напишите, чему равен его коэффициент k: 

2.      Упростить выражение:

а)  5х²у – 8х²у + х²у         б)          в)          г)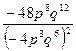  

3.      Незнайка, отправляясь на Луну на воздушном шаре, взял для балласта несколько мешков с песком. Когда воздушный шар первый раз пошел на снижение, незнайка выбросил  всех мешков, во второй раз он выбросил еще 60% от оставшихся мешков, а в третий раз – последние 4 мешка. Сколько всего мешков с песком брал с собой Незнайка?

4.      Найдите значение выражения

-2ху⁴х² + 3х³у²2у² – х²у(-ху³)          при  х = ;   у = 2

5.      Решите уравнение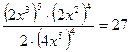       

 

 

 

Контрольная работа № 5

Вариант 2

1.      Приведите одночлен к стандартному виду и напишите, чему равен его коэффициент k:

2.      Упростить выражение:

а)  ху² – 13ху² + 5ху²         б)          в)          г)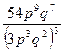  

3.      Малыш подарил Карлсону банку клубничного варенья. Карлсон в первый день съел 25% всего варенья, во второй он съел  от оставшегося варенья, а в третий – доел последние 270г. Сколько всего граммов варенья было в банке?

4.      Найдите значение выражения

2a²b³(-1,5a³b) + 5a⁴b⁴a + a²(-b)⁴a³при  b = ;   a = -3

5.      Решите уравнение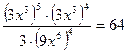       

    

Контрольная работа № 6

Вариант 1

 

1.      Найти многочлен р(х) и записать его в стандартном виде, если:

р(х) = р₁(х) + р₂(х) – р₃(х)     и    р₁(х) = -2х² + 3х;       р₂(х) = 4х² – 3;     р₃(х) = 2х – 4.

2.      Выполните действия:

а)  4ху(2х + 0,5у – ху);           б)  (х – 3)(х + 2);        в)  (24х²у + 18х³) : (-6х²)

3.      Упростите выражение, используя ФСУ:  (2р – 3)(2р + 3) – (р – 2)².

4.      Найти три последовательных натуральных числа, если известно, что квадрат большего из них на 34 больше произведения двух других.

5.      Докажите, что значение выражения не зависит от значения переменной:  5х³ – 5(х + 2)(х² – 2х + 4)

 

 

 

 

 

 

Контрольная работа № 6

Вариант 2

 

1.      Найти многочлен р(х) и записать его в стандартном виде, если:

р(х) = р₁(х) + р₂(х) – р₃(х)     и    р₁(х) = 2х² - 5х;       р₂(х) = 3х² + 1;     р₃(х) = х – 2.

2.      Выполните действия:

а)  -5ху(3х² - 0,2у² + ху);           б)  (х – 5)(х + 4);        в)  (35х³у - 28х⁴) : 7х³

3.      Упростите выражение, используя ФСУ:  (р + 3)² - (3р - 1)(3р + 1).

4.      Найти три последовательных натуральных числа, если известно, что квадрат меньшего из них на 47 меньше произведения двух других.

5.      Докажите, что значение выражения не зависит от значения переменной:   2х³ – 2(х - 3)(х² + 3х + 9)

 

Контрольная работа № 7

Вариант 1

1.      Разложить на множители:

а)  3х² – 12х              б)  2а + 4b – ab – 2b²         в)  4х² – 9   г)  х³ – 8х² + 16х

2.      Сократите дробь:

а)                               б) 

3.      Решите уравнение        (х – 4)² – 25 = 0

4.      Вычислите рациональным способом  

5.      Докажитетождество:   a³ + 3a²b + 3ab² + b³ = (a + b)³

 

Контрольная работа № 7

Вариант 2

1.      Разложить на множители:

а)  4х² + 8х              б)  3а - 6b + ab – 2b²         в)  9х² – 16   г)  х³ + 18х² + 81х

2.      Сократите дробь:

а)                               б) 

3.      Решите уравнение        (х + 2)² – 49 = 0

4.      Вычислите рациональным способом  

5.      Докажитетождество:   a³ - 3a²b + 3ab² - b³ = (a - b)³

 

Контрольная работа № 8

Вариант 1

1^о. Постройте график функции у = х². С помощью графика найдите

а) значение функции при значении аргумента, равном -2;  1;  3; б) значение аргумента, если значение функции равно 4;

в) наибольшее и наименьшее значения  функции на отрезке [-1;2];

2^о. Решите графически уравнение х² = 2х + 3

3^о. Дана функция y = f(x), где f(x) = x². При каких значениях х верно равенство

f(x - 4) = f(x + 3)?

4.  Дана функция y = f(x), где                 х²,  если -3 £  х  £ 2,

                                                                             -х + 6,  если  х  >  2.

Используя график функции, установите:

а) область определения функции;б) наибольшее и наименьшее значения  функции

в) является ли функция непрерывной: если нет, то в каких точках терпит разрыв;

г) промежутки возрастания и убывания функции;

д) при каких значениях аргумента          у = 0,       у < 0,       y> 0.

5.      Постройте график функции

Контрольная работа № 8

Вариант 2

1.      Постройте график функции у = х². С помощью графика найдите

а) значение функции при значении аргумента, равном -3;  -1;  2; б) значение аргумента, если значение функции равно 9;

в) наибольшее и наименьшее значения  функции на отрезке [-3;2];

2^о. Решите графически уравнение х² = 4х - 3

3^о. Дана функция y = f(x), где f(x) = x². При каких значениях х верно равенство

f(x - 2) = f(x + 5)?

4.  Дана функция y = f(x), где                     х + 3,  если   х < -1,

х²,  если  -1£  х  £   3.

Используя график функции, установите:

а) область определения функции;б) наибольшее и наименьшее значения  функции

в) является ли функция непрерывной: если нет, то в каких точках терпит разрыв;

г) промежутки возрастания и убывания функции;

д) при каких значениях аргумента        у = 0,       у < 0,       y> 0.

5.Постройте график функции

Итоговая контрольная работа

Вариант 1

1.      Постройте график функции y = - 3x + 6

     Используя график функции, установите:

a) наибольшее и наименьшее значения  функции на отрезке [1;2];

     б) значения аргумента, при которых      у = 0,       у < 0.

2.      Решите  уравнение  (х – 3)(х + 2) – (х – 1)(х + 1) = 3х + 7

3.      Сократите дробь:      а)                                 б) 

4.      Расстояние между двумя пристанями по реке равно 27км. Катер проплывает его по течению реки за 1,5 ч, а против течения за 2ч 15м. Найти собственную скорость катера и скорость течения реки.

5.      Постройте график функции y = f(x), где

х²,  если   х £ 2,

                                                    -2х + 8,  если    х  >  2.

    С помощью графика определите, при каких значениях р уравнение f(x) = р имеет два корня.

Итоговая контрольная работа

Вариант 2

1.      Постройте график функции y = x + 1

     Используя график функции, установите:

a) наибольшее и наименьшее значения  функции на отрезке [0;3];

     б) значения аргумента, при которых     у = 0,       у > 0.

2. Решите  уравнение  (х + 4)² - (х + 1)(х – 2) = 2х – 3

3. Сократите дробь:       а)                                 б) 

4.Катер за 1ч 20м проплывает  по течению реки 24км, а против течения за 1,5ч на 3км меньше  Найти собственную скорость катера и скорость течения реки.

5. Постройте график функции y = f(x), где 

 

х + 2,  если   х < -1,

x²,  если    х   ³ -1.

    С помощью графика определите, при каких значениях р уравнение f(x) = р имеет два корня.

 

 

 

 

Сокращения, используемые в рабочей программе:

Типы уроков:

УОНМ — урок ознакомления с новым материалом.

УЗИМ — урок закрепления изученного материала.

УПЗУ — урок применения знаний и умений.

УОСЗ — урок обобщения и систематизации знаний.

УПКЗУ — урок проверки и коррекции знаний и умений.

КУ — комбинированный урок.

ЗУ — зачётный урок.

Виды контроля:

ФО — фронтальный опрос.

ИРД — индивидуальная работа у доски.

ИРК — индивидуальная работа по карточкам.

СР — самостоятельная работа.

ПР — проверочная работа.

МД — математический диктант.

Т – тестовая работа.

 

 

 

 

 

Календарно-тематическое планирование

№

Дата

Тема урока

Кол-во часов

Тип урока

Материально-техническая база

Планируемые результаты

Вид контроля

Д/З

Повторение курса 6 класса - 4

1-2

Повторение

2

КУ

-уметь решать примеры на все действия с дробями и рациональными числами; - уметь решать задачи с помощью уравнений, на проценты, пропорции; -уметь решать уравнения методом переноса слагаемых

ПР СР

3-4

Нулевой срез

2

ЗУ

-учащиеся демонстрируют знания материала курса математики 6 класса, умение работать с рациональными числами, решать задачи на проценты, решать уравнения, пропорции, решать задачи, составляя уравнения

Т1[7]

Тема 1

Математический язык. Математическая модель- 12

5-6

Числовые и алгебраические выражения.

2

КУ УПКЗУ

-уметь выполнять арифметические действия с рациональными числами

ФО [1] ИРД СР1[6],СР1,2[9]

7-8

Что такое математический язык

2

КУ УЗИМ

-осуществлять в выражениях подстановки и выполнять соответствующие вычисления

ФО [1] ПР ,СР2,3[6] СР4[9]

9-10

Что такое математическая модель

2

КУ УПКЗУ

-уметь описывать реальные ситуации словами, алгебраически, графически; свободно оперировать с любыми видами математических моделей.

ФО [1] ИРД СР4[6]

11-13

Линейное уравнение с одной переменной

3

УПЗУ КУ УЗИМ

-уметь решать уравнения; -уметь пользоваться свойствами уравнений -знать общий вид линейного уравнения; -уметь решать уравнение вида  при, при  и , при  и

ФО [1] ИРД СР 8,9[9]

14-15

Координатная прямая   Обобщение, повторение

2          2

УОНМ КУ

-иметь представление о координатной прямой, числовых промежутках на ней; -уметь изображать различные числовые промежутки и читать их

ФО [1] СР27[6]

16

Контрольная работа №1

1

ЗУ

- уметь выполнять арифметические действия с рациональными числами; -уметь упрощать выражения, применяя тождественные преобразования; -уметь составлять математические модели и работать сними; -уметь решать уравнения, сводящиеся к линейным; -уметь решать задачи на составление уравнений

КР1[5] КР1,2[9]

Тема 2

Линейная функция- 14

17-18

Координатная плоскость

2

КУ УОНМ

презентация

-знать определение понятий: прямоугольная система координат, начало координат, координатные оси, координатные углы, абсцисса точки, ордината точки; -знать алгоритмы построения точки на координатной плоскости по заданным координатам, определения  координат заданной точки и уметь их применять.

ФО [1] ИРД СР28[6] СР11[9]

19-21

Линейное уравнение с двумя переменными и его график

3

УОНМ КУ УПЗУ УОСЗ

презентация

-иметь представление об уравнении с двумя переменными его решении; -уметь применять алгоритм для построения графика уравнения  ax + by + c = 0, где a≠0, b≠0

ФО [1] ИРД ПР СР29[6]

22-25

Линейная функция и её график

3

УОНМ КУ УПЗУ УПКЗУ

-понимать отличие функции от других зависимостей; -уметь по значению аргумента находить значение функции по графику; -уметь задавать формулой зависимость одной величины от другой; -выражать из формул одну переменную через остальные; -отличать линейную функцию от других; -уметь строить график линейной функции.

ФО [1] ИРД ПР СР30,31[6] СР12,13[9] Т9[7]

26-27

Линейная функцияy=kx.(С.р)

2

КУ УПЗУ

- уметь по значению аргумента находить значение функции, заданной формулойy=kx; -иметь представление о расположении графиков функций y=kx иy=kx+m; -уметь строить график функцииy=kx

ФО [1] ИРД СР32[6] СР14[9]

28-29

Взаимное расположение графиков линейных функций.

2

УОНМ КУ УПКЗУ УОСЗ

-знать о параллельности и пересечении графиков; -уметь находить точку пересечения графиков функций

ФО [1] ИРД СР 16,17[9]

30

Контрольная работа №2.

1

-строить график линейной функции; - уметь по графику находить значения x  и y; -определять взаимное расположение графиков функций

КР7[5] КР3[9]

Резерв

1

Тема 3

Системы двух линейных уравнений с двумя переменными- 12

31-32

Основные понятия.

2

УОНМ КУ

-знать, какое уравнение называется линейным уравнением с двумя переменными; -иметь представление о системе двух уравнений с двумя неизвестными и её графическом решении; -уметь определять является ли пара чисел решением уравнения; -уметь решать графическим методом систему уравнений.

ФО [1] ИРД СР36[6] СР45[9]

33-35

Метод подстановки.

2

УОНМ КУ УЗИМ УПЗУ

-знать алгоритм решения систем двух линейных уравнений способом подстановки

ФО [1] СР37[6] СР46[9]

36-38

Метод алгебраического сложения.

3

УОНМ КУ УЗИМ УПЗУ

-знать алгоритм решения систем двух линейных уравнений способом сложения

ФО [1] СР38[6] СР47[9]

39-41

Решение текстовых задач с помощью систем уравнений

3

УОНМ КУ УЗИМ УПЗУ

-уметь решать задачи с помощью систем двух линейных уравнений с двумя переменными

СР48,49,50[9] СР39[6]

42

Контрольная работа №3

1

ЗУ

-уметь решать системы уравнений графическим методом,методом подстановки и методом сложения; -решать задачи на составление систем; -уметь задавать линейную функцию формулой по двум точкам

КР8[5] КР9[9]

Тема 4

Степень с натуральным показателем и её свойства- 7

43

Степень с натуральным показателем.

1

КУ

-уметь записывать произведение в виде степени; -уметь возводить в степень отрицательные числа; -выполнять возведение в степень

ФО ИРД

44

Таблица основных степеней.

1

КУ

-знать таблицу основных степеней; -уметь работать с таблицей основных степеней, -уметь определять знак степени по её показателю.

МД СР5[6] СР18,19[9]

45

Свойства степени с натуральными показателями

1

УОНМ КУ УЗИМ

-знать свойства степени с натуральным показателем; -уметь доказывать свойства степени с натуральным показателем; -уметь применять свойства степени с натуральным показателем: an∙am=an+m, an:am=an-m

ФО ИРД СР6[6] СР20[9]

46-47

Умножение и деление степеней с одинаковым показателем

2

КУ УОСЗ

-знать свойства степениan∙bn=(ab)nи  an:bn=(a:b)n и уметь их применять

МД ИРД СР21,22[9]

48

Степень с нулевым показателем

2

КУ

- иметь представление о степени с нулевым показателем, -уметь работать со степенями с нулевым показателем

СР7[6]

49

Контрольная работа №4

1

ЗУ

-уметь применять все свойства степени в комплексе

КР4[9] КР2[5]

Тема 5

Одночлены. Арифметические операции над одночленами–8

50

Понятие одночлена. Стандартный вид одночлена.

1

УОНМ КУ

-знать определения одночлена, его стандартного вида, коэффициента одночлена; -уметь приводить одночлен к стандартному виду; -уметь определять коэффициент и степень одночлена.

МД ПР СР23[9]

51-52

Сложение и вычитание одночленов

2

УОНМ КУ УЗИМ

-знать какие из одночленов называются подобными; -уметь складывать и вычитать подобные одночлены.

ФО СР8,9[6] Т3[7]

53-54

Умножение одночленов. Возведение одночлена в натуральную степень

2

КУ УОСЗ УПЗУ

-знать и уметь применять свойства степени: -уметь перемножать одночлены; -уметь возводить одночлены в степень, применяя свойства (аb)n=an∙bnи (аm)n=anm

ФО [1] ИРД СР 24[9] СР10[6]

55-56

Деление одночлена на одночлен

2

КУ УЗИМ УОСЗ

- уметь делить одночлен на одночлен

ФО ИРД СР11[6] Т4[7]

57

Контрольная работа №5

1

-уметь работать с одночленами, применяя свойства степеней, выполнять все действия с одночленами

КР3[5]

Тема 6

Многочлены. Арифметические операции над многочленами- 17

58-59

Основные понятия

2

КУ УЗИМ

-уметь приводить подобные члены; -записывать в стандартном виде многочлен

ФО [1] ИРД СР12[6] СР25[9]

60-61

Сложение и вычитание многочленов.

2

КУ УПЗУ

-знать как раскрыть скобки со знаком «плюс» или «минус» перед ними; -уметь приводить подобные слагаемые

ФО [1] ИРД,СР13[6], СР26,27[9]

62-63

Умножение одночлена на многочлен.

2

КУ УПЗУ УПКЗУ

-знать правило умножения одночлена на многочлен; -выполнять умножение по правилу

ПР СР14,15[6], СР28,29,30[9]

64-65

Умножение многочлена на многочлен.

2

КУ УПЗУ УОНМ

-знать правило умножения многочлена на многочлен; -выводить формулу (a+b)(c+d)=ac+bc+ad+bd

ФО [1] ИРД СР16[6] СР33,34[9] Т5[7]

66

Контрольная работа №6

1

-проводить сложение и вычитание многочленов; -выполнять умножение одночлена на многочлен; -выполнять умножение многочлена на многочлен

КР4[5] КР5[9]

Формулы сокращенного умножения

5

67-68

Возведение в квадрат суммы и разности двух выражений.

2

КУ УПЗУ

-знать формулы: -уметь представлять в виде многочлена квадрат суммы и разности

ИРД ИРК СР17[6] СР37,38[9]

69-70

Разность квадратов

2

КУ УПЗУ УОСЗ

-уметь выполнять умножение разности двух выражений на их сумму по формуле: -знать формулу:  ; -уметь правильно применять формулу

ФО [1] ИРД СР18[6] СР40[9]

71

Разность кубов и сумма кубов.

1

КУ УОСЗ

-знать формулы: ; -уметь выделять неполный квадрат суммы или разности

ФО [1] ИРД СР19[6]

72-73

Деление многочлена на одночлен

2

КУ УПЗУ

-знать правило деления многочлена на одночлен; -уметь применять правило деления многочлена на одночлен.

ИРК Т6[7] СР41[9]

74

Контрольная работа №7

1

-уметь пользоваться формулами сокращенного умножения и используя их упрощать выражения; -уметь выполнять арифметические действия с многочленами.

КР5[5]

Тема 7

Разложение многочленов на множители– 20

75

Что такое разложение многочлена на множители и зачем оно нужно

1

КУ

-знать, что есть многочлены, которые можно представить в виде произведения нескольких множителей; -знать для чего нужно уметь раскладывать многочлен на множители

ФО [1] ИРД

76-78

Вынесение общего множителя за скобки

3

КУ УЗИМ УПЗУ

-знать алгоритм отыскания общего множителя нескольких одночленов; -уметь применять алгоритм отыскания общего множителя нескольких одночленов; -уметь выносить общий множитель за скобки.

МД ИРД СР20[6] СР32[9]

79-81

Способ группировки.

3

УОНМ УПЗУ УПКЗУ УОСЗ

-знать и применять алгоритм разложения многочлена на множители способом группировки

ИРД ИРК СР 35[9] СР21[6]

82-86

Разложение многочленов на множители с помощью формул сокращённого умножения

4

КУ УЗИМ УПЗУ УОСЗ УПКЗУ

-знать формулы сокращённого умножения; -уметь применять формулы сокращённого умножения для разложения на множители многочленов

ФО [1] МД ИРД ПР СР22,23,24[6] СР39,42[9] Т7[7]

87-89

Комбинированные приёмы, связанные с разложением многочленов на множители.

3

КУ УПЗУ УОНМ УПКЗУ УЗИМ

-уметь применять последовательно несколько способов для разложения; -знать, что начинать преобразования следует с вынесения общего множителя за скобки; -уметь применять метод выделения полного квадрата

ИРД СР 25[6] СР44[9] Т8[7]

90

Контрольная работа №8

1

ЗУ

-правильно определить способ для разложения на множители; -знать формулы сокращенного умножения

КР6[5] КР7,8[9]

91-93

Сокращение алгебраических дробей

3

УОНМ УЗИМ УПЗУ

-знать определение алгебраической дроби, числителя и знаменателя, -уметь сокращать алгебраические дроби.

ФО[1] ИРД, СР26[6] СР51,52[9]

94

Тождества

1

КУ

-знать определения тождества, тождественных преобразований, -уметь выполнять тождественные преобразования .

ФО[1]

Тема 8

Функция У = X2 -7

95-96

Функция У = X2 и её график

2

УОНМ КУ

-иметь представление о функции У = X2  и её графике, -знать название графика квадратичной функции, его особых элементов -уметь строить график квадратичной функции.

ФО[1] СР33[6]

97-98

Графическое решение уравнений

2

УОНМ КУ УЗИМ

-знать алгоритм графического решения уравнений, -уметь применять алгоритм графического решения уравнений.

МД СР34[6]

99-100

Что означает в математике запись у =f(x).

2

УОНМ КУ УЗИМ

-знать свойства функций, понятие кусочной функции; -уметь читать графики функций.

ФО[1] ИРД СР35[6] Т10[7]

101

Контрольная работа №9

1

ЗУ

-уметь строить график квадратичной функции; -уметь применять алгоритм графического решения уравнений.

КР8[5]

Итоговое повторение курса алгебры 7 класса- 7

102

Преобразование выражений.

1

КУ

-уметь пользоваться всеми арифметическими операциями над числами

ФО ИРД

103

Линейная функция и её график.

1

КУ

-уметь строить график линейной функции и работать по нему

ФО ИРД

104

Степень и её свойства.

1

КУ

-знать все свойства степени; -уметь упрощать выражения, используя свойства степени

ФО ИРД

105

Произведение многочленов.

1

КУ УПЗУ

-уметь перемножать многочлены по правилу

ФО ИРД

106

Формулы сокращенного умножения.

1

КУ УПЗУ

-знать формулы сокращенного умножения и их вывод; -уметь их применять.

ФО ИРД

107

Решение систем линейных уравнений.

1

КУ

-уметь применять способы решения систем линейных уравнений.

ФО СР40[6]

108

Итоговая контрольная работа №10

1

ЗУ

-уметь применять все полученные знания за курс алгебры 7 класса.

КР10[5] КР(итог.)1,2[9] Т11[7]