
Блоки и взаимообратные блоки решения геометрических задач в теме «Равенство треугольников».
Одной из главных задач, стоящих сегодня перед школой, является задача повышения качества учебно-воспитательного процесса. Учебная деятельность школьников организуется и направляется учителем, имеющем в своем распоряжении комплекс средств обучения. От мастерства и опыта учителя, от содержания учебного материала и методической системы, в которой он подается, зависит результат учения. Поэтому для повышения эффективности управления учебной деятельностью школьников необходимо постоянно искать пути совершенствования форм и методов обучения.
Особенно важную роль в обучении математике играют задачи. Они рассматриваются и как цель, и как средство обучения. Таким образом, поставленная учителем общая цель (например, систематизация изученного материала, демонстрация определенного метода рассуждений, закрепление новых понятий и т.д.) должна и может быть решена лишь с помощью специально подобранных задач. Причем залогом успеха в достижении цели является построение целой системы взаимосвязанных задач. Известный математик и педагог Г. Фройденталь в книге «Математика как педагогическая задача» 'пишет: «Здоровым принципом является изучать не изолированные крохи, а согласованные разделы. То, что взаимосвязано, легче изучается и легче удерживается». И даже из психологии известно, что цепочка взаимосвязанных задач лучше воспринимается, запоминается и усваивается школьниками, чем набор изолированных друг от друга задач.
Систему взаимосвязанных задач мы и будем называть, блоком задач. Задавая учащимся, блок задач, то есть, задавая набор упражнений, упорядоченных в соответствии с определенными целесообразными принципами, мы тем самым определяем систему действий обучаемых, намечаем структуру познавательного процесса. Таким образом, блок задач, во- первых, заключает в себе цель, поставленную учителем, и, во-вторых, еще и намечает структуру и способы ее достижения.
Анализ научно-методической литературы показывает, что идея рассмотрения взаимосвязанных укрупненных задач в методике преподавания геометрии не нова. Примеры создания задач, объединяемых авторами в блоки, системы, совокупности и т.д., можно встретить в работах Э.Г.Готмана, Г.В.Дорофеева, Т.М.Калинкиной ,Г.И.Саранцева , П.М.Эрдниева и многих других. Принципы их образования у разных авторов нередко различаются.
Если рассмотреть укрупненное упражнение П.М.Эрдниева – «главное оружие теории УДЕ», представляющее собой «многокомпонентное задание, образующееся из нескольких логически разнородных, но психологически состыкованных в некоторую целостность частей, например:
а) решение обычной «готовой» задачи;
б) составление обратной задачи и ее решение;
в) составление аналогичной задачи по данной формуле (тождеству) или уравнению и решение ее;
г) составление задачи по некоторым элементам, общим с исходной задачей;
д) решение или составление задачи, обобщенной по тем или иным параметрам исходной задачи», то нетрудно заметить, что оно также представляет собой блок взаимосвязанных задач, в котором одна задача (представленная в пункте А) является основной, а другие – ее производными, полученными на ее основе.
Такой же (или похожий) принцип составления блоков задач выделялся в диссертационных исследованиях Т.М.Калинкиной, Е.В.Селезневой, в работах Е.С.Канина и др. Помимо этого в методической литературе были определены и другие способы объединения задач в блоки. Однако независимо от того или иного способа ученые, рассматривающие такие задачи, указывали на многие их достоинства и широкие возможности применения в обучении школьников. Отмечалось, что цепочки таких задач могут объединять разделы одной учебной темы и использоваться на уроках обобщения знаний, а могут углублять изучаемые зависимости, охватывая уже несколько тем (Г.И.Саранцев). При этом их решение будет способствовать развитию у школьников интереса к геометрии (И.А.Кушнир), критичности их мышления (Т.М.Калинкина) и творческих способностей (Э.Г.Готман), формированию элементов исследовательской деятельности: умения целенаправленно наблюдать, сравнивать и обобщать, выдвигать, доказывать или опровергать гипотезу (Г.В.Токмазов) и т.д. Д.Пойа, например, выделяет 6 основных способов варьирования задачи: обобщение, специализацию, аналогию, «разложение» и составление новых комбинаций, введение вспомогательных элементов, «возвращение» к определениям.
Как показывает анализ научно-методической литературы, блоки взаимосвязанных задач не раз становились объектом исследования многих авторов, что уже было отмечено выше. Изучению подверглась и методика обучения учащихся навыкам работы с такими блоками.
Так, в диссертационном исследовании Т.М.Калинкиной рассматривалась методика включения так называемых динамических задач в процесс обучения школьников геометрии. Она, по словам автора, предполагает реализацию трех основных этапов:
1.«работу по готовым, составленным учителем, динамическим задачам;
2. совместную деятельность учителя и ученика по получению динамических задач;
3.организацию деятельности по самостоятельному составлению динамических задач учащимися».
Подобные этапы справедливы и для использования в учебном процессе блоков укрупненных задач. Блоком укрупненных задач назовем совокупность нескольких задач, взаимосвязанных между собой по линии укрупнения своих решений, осуществляемой через укрупнение действий, адекватных этим решениям. Т.е. темы учебной программы можно объединять в различные блоки в зависимости от цели урока.
Таким образом, связи между задачами такого блока носят не столько содержательный (как в блоках, составляемых Э.Г.Готманом, И.А.Кушниром и др.), сколько процессуальный характер. При этом данная связь характеризуется, в первую очередь, не наличием общей закономерности или общего метода решения блочных задач, а тем, что каждая последующая из них в данном блоке расширяет (укрупняет) решение любой из предшествующих ей в нем задач посредством выполнения одного или более новых действий. Другими словами, решение каждой последующей в блоке задачи содержит в себе как составную часть решение одной из предшествующих ей в нем задач.
Е.С. Канин приводит примеры формулировки и решения задач, являющихся продолжением темы данной задачи. К ним автор относит «задачи, которые получаются из исходной (исходных):
ü заменой части данных в исходной задаче другими данными без замены заключения задачи;
ü при обобщении данных и искомых;
ü путем специализации данных и искомых;
ü добавление новых заключений при сохранении данных;
ü заменой части данных исходной задачи ее искомыми (часть данных принимается за искомые, а некоторые искомые считаются данными), т.е. путем обращения задачи».
И.Е. Дразнин в своей работе для построения взаимосвязанных задач использует первый способ, указанный Е.С. Каниным. Одним из важнейших принципов построения систем упражнений, по мнению И.Е. Дразнина, является «…принцип варьирования – составления такой последовательности упражнений, в которой каждое последующее получено из предыдущего или одного из предыдущих изменением условия или параметра». Делая ссылки на опыт применения таких задач, автор отмечает, что «после нескольких месяцев работы учащиеся довольно успешно сами варьируют условия, это развивает фантазию, интуицию, логику, снижает диктат учителя». Следовательно, описанный И.Е. Дразниным способ дает ощутимый результат.
По мнению Д.Ф. Изаака, по ходу решения любой геометрической задачи обнаруживаются различные свойства соответствующей геометрической фигуры, в том числе такие, которые в процессе решения не используются. Исследование задачи начинается тогда, когда после ее решения выявляются новые свойства полученного результата. В некоторых случаях они могут быть достаточно интересными и использоваться для составления новых задач и различного рода обобщений. Ученый выделяет приемы составления новых задач: на основе обнаруженных в процессе решения исходной задачи свойств объектов, присущих условию; на основе обобщения результата, полученного при решении исходной задачи; путем составления задачи, обратной исходной; с помощью замены одного из условий исходной задачи.
Э.Г. Готман, И.Я. Кушнир и Б.Ф. Харитонов в своих работах описывают задачи (серии задач), связанные одной геометрической конфигурацией. У Э.Г. Готмана и И.Я. Кушнир такая конфигурация – объединение треугольника и квадрата в различных вариациях. Оба автора предлагают примеры блоков, но не раскрывают ни методику их получения, ни принципы организации задач в блоки, ни методику работы с ними.
В методической литературе можно обнаружить и другие способы интеграции методов при решении блоков укрупненных задач. А именно:
1.Сочетание элементов разных методов при решении той или иной укрупненной задачи (часть задачи решается посредством одного метода решения, а часть – посредством другого метода).
2.Решение одной и той же задачи в блоке разными методами (как самостоятельная, задача полностью решается посредством одного метода, а как часть расширенной задачи – посредством другого метода).
На основе этой же идеи блоки задач описывает Г.В. Токмазов. Автор предлагает «…использовать одну задачу в качестве основной» и перечисляет несколько способов составления к ней подзадач:
-«…подобрать новые вопросы (требования) к условию задачи;
-в соответствии с требованиями исходной задачи, составить более общую задачу;
-сформулировать вопросы, которые раскрывают частные крайние случаи исходной задачи;
-рассмотреть условие (или требование), которое является отрицанием условия (или требования) первоначальной задачи;
-составить задачу, которая решалась бы с помощью контрпримера;
-составить задачу, которая решалась бы различными способами»
Одной из характерных особенностей системы укрупнения знаний выступает применение "метода обратных задач". Работу над задачей целесообразно завершать получением ответа к ней; надо приемом обращения составлять и решать новую, обратную задачу, извлекая тем самым дополнительную информацию, заключающуюся в связях между величинами исходной решенной задачи. При подборе упражнений в учебниках структурно противоположные задачи зачастую рассматриваются отдельно друг от друга, раздельно во времени, нередко в виде особой темы. Между тем обращение задания позволяет сравнить прямую и обратную задачи в пределах единого "укрупненного" задания. Обращение задания также позволяет определить в геометрии, например, является ли то или иное свойство характеристическим для данной фигуры. В частности доказать характеристическое свойство - это значит доказать прямую и обратную теоремы.
В связи с этим мы хотим сказать, что геометрия предполагает решение учащимися задач различных типов, но обязательным этапом решения любой из них является доказательство того или иного положения. Для этого возникает необходимость выявления общих приемов поиска доказательства, с которыми необходимо знакомить учащихся.
Например, в теме «Равенство треугольников» признаки равенства треугольников требуют доказательства.
Итак, самыми первыми теоремами в курсе геометрии 7 класса различных авторов учебников существуют теоремы о равенстве треугольников.
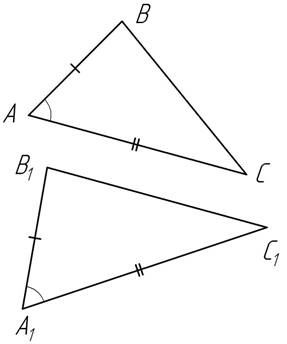
Теорема 1 (первый признак равенства треугольников). Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны (рис.1).
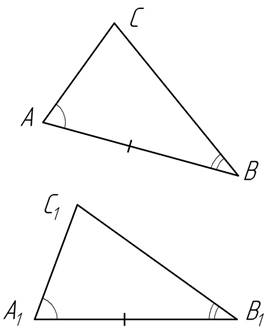
Теорема 2 (второй признак равенства треугольников). Если два угла и прилежащая к ним сторона одного треугольника соответственно равны двум углам и прилежащей к ним стороне другого треугольника, то такие треугольники равны (рис.2).
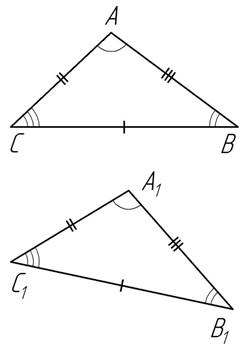
Теорема 3 (о равенстве углов треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то соответственные углы этих треугольников равны (рис.3).
Чтобы учащимся 7 класса было легче и доступнее запомнить и доказать вышеуказанные теоремы необходимо воспользоваться методом составления блока взаимосвязанных задач.
Для этого в соответствии с изложенным в учебнике материалом по данной теме строим соответствующий блок, содержащий части, удовлетворяющие условиям;
o каждая часть состоит из предложений, входящих в доказательство теоремы;
o каждая часть представляет собой логически законченный вывод из одной или нескольких посылок последнего входящего в предыдущую часть предложения;
o каждая часть должна содержать не только предложения, полученные в результате выводов, но и аксиомы или ранее доказанные теоремы, предложения, истинные в силу определения;
o каждое предложение из доказательства должно входить хотя бы в одну из частей. Последнее предложение должно входить в последнюю из частей;
o последнее предложение каждой из частей должно содержаться хотя бы в одной из последующих частей;
o каждая часть должна представлять собой вывод некоторого свойства конкретного объекта, входящего в систему объектов, рассматриваемых в данном доказательстве.
Полученный в результате составления в соответствии с вышеуказанными требованиями блок задач поможет учащимся выявить закономерности в теме «Равенство треугольников», тем самым они усвоят доказательства теорем без особого труда и смогут осознанно их воспроизвести.
В действующих учебниках не все задачи для этого подходят, но именно эти задачи обладают большой дидактической ценностью. Вообще на удачно подобранной задаче можно изучить многие вопросы курса геометрии. Эти задачи обладают также и другой дидактической ценностью, так как на этих задачах учащиеся обучаются умению чертить и анализировать чертеж, у них развивается «геометрическое видение», оттачивается интуиция. Ведь чаще всего уроки строятся по принципу «от простого к сложному», начиная с простейших задач, те которые может понять и решить «средний» ученик, затем сложность задачи увеличивается и на одном из уроков блока – модульном, т.е. урок одной задачи, разбираем ее решение и составляем подзадачи. Успеху делу способствует то, что внимание учащихся целиком и полностью сконцентрированное на материале темы.
Эту ситуацию описывает Н.С. Мельник в своей работе: «Многие задачи геометрии взаимосвязаны, т.е. решения их строятся на одной общей идее. К сожалению, специфика школьного курса, и в первую очередь его насыщенность, не позволяют в полной мере раскрыть перед учащимися эту особенность геометрических задач». Решение этой проблемы автор видит во внеклассных занятиях (математических кружках). Н.С. Мельник приводит пример группы задач, построенных на общей идее, но не описывает, как он ее получил.
Поэтому проблема создания циклов, блоков взаимосвязанных задач, различных по формулировке, по сюжету, но имеющих общее дидактическое назначение, служащих достижению поставленной цели, является актуальной.
Данную проблему в своих работах рассматривали
Э.Г. Готман,
Г.В. Дорофеев, Т.М.Калинкина, К.И. Камбаров, Е.С. Канин, И.Я. Куприянова, Н.С.
Мельник, В.И. Мишин, Н.Г. Рыженко , Г.И. Саранцев , Б.Ф. Харитонов и др.
Для примера рассмотрим более подробно, какие блоки и каким именно образом можно использовать в процессе обучения учащихся решению задач по геометрии методом, основанным на признаках равенства треугольников, начиная с этапа работы школьников с готовыми блоками задач.
Начинать реализовывать данный этап наиболее полно, на наш взгляд, можно при изучении только второго признака равенства треугольников. К моменту знакомства учащихся с первым признаком их запас теоретических знаний по геометрии настолько мал, что реальным становится составление лишь небольших и не слишком разнообразных блоков. Например:
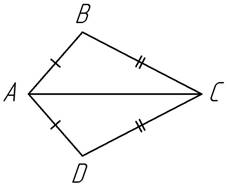
1.1. Треугольники АВС и ADC равны. Запишите все соотношения, из которых следует равенство указанных треугольников.
1.2. Прямые AD и ВС пересекаются в точке О так, что АО=ОD, ВО=ОС. Докажите, что DАВО = DDCО.
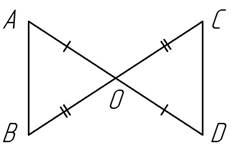
1.3. Прямые АD и ВС пересекаются в точке О, так что АО=ОD, ВО=ОС. Какое из возможных соотношений между элементами треугольников АВС и DСB следует взять, чтобы как можно проще доказать равенство этих треугольников?
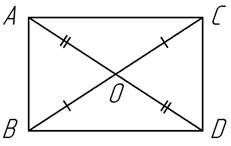
1.4. В треугольниках АВС и DBC АС=ВD, ÐACB=ÐDBC. Верно ли, что DАВС = DDBC?
Зависимость решения одной задачи от решения другой, предполагает последовательное укрупнение соответствующих им действий, способна значительно облегчить для школьников процесс решения каждой новой задачи, а также усвоить изучаемый теоретический материал.
Подобным образом учащимся можно предлагать и другие готовые блоки укрупнения задач. При этом за исходную задачу (или за промежуточную) возможно принять какую-либо задачу, предлагаемую в школьном учебнике. Например, используя приемы укрупнения чертежа, постановки нового требования, а также конкретизации условия задачи посредством введения новых числовых данных, можно образовать такой блок:
2.1 В треугольниках АВС и А1В1С1 медианы АМ и А1М1 равны, ВС= В1С1, ÐАМВ=ÐА1М1В1. Докажите, что DАВС=DА1В1С1 (№ 161 [7])
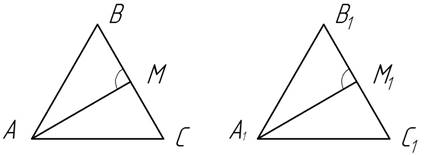
2.2 В треугольниках АВС и А1В1С1 медианы АМ и А1М1 равны, ВС= В1С1, ÐАМВ=ÐА1М1В1. На сторонах АС и А1С1 взяты точки К и К1, так что АК=А1К1. Докажите, что DКВС=DК1В1С1.
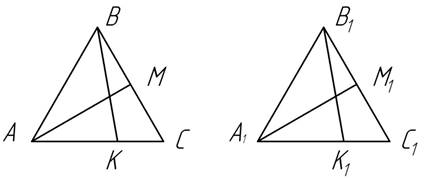
2.3. В треугольниках АВС и А1В1С1 медианы АМ и А1М1 равны, ВС= В1С1, ÐАМВ=ÐА1М1В1. На сторонах АС и А1С1 взяты точки К и К1, так что АК=А1К1. Докажите, что DАВК=DА1В1К1.
В одном таком блоке собраны задачи, решения которых требует от учащихся применения достаточного объема геометрических знаний. То есть, решение каждой последующей задачи будет способствовать как повторению учащимися всего (или почти всего) ранее изученного материала, так и закреплению ими только что изученного. При этом новые знания школьников будут органически вплетаться в систему уже имеющихся у них знаний, способствуя их систематизации и обобщению. Решение задач из подобных блоков можно рассматривать и как осуществление пропедевтического курса к изучению школьниками нового материала. Так, решение указанного выше блока задач 2.1 – 2.3 может быть использовано как мотивационный этап для показа школьникам необходимости изучения второго признака равенства треугольников, если к нему добавить, к примеру, следующие задачи:
2.4. В треугольниках АВС и А1В1С1 медианы АМ и А1М1 равны, ВС=В1С1, ÐАМВ=ÐА1М1В1. На сторонах АС и А1С1 взяты точки К и К1 так, что АК=АК1. Докажите, что DАОВ=DА1О1В1, где О, О1 – точки пересечения медиан АМ, А1М и ВК, В1К1 соответственно.
2.5. В равносторонних треугольниках АВС и А1В1С1 медианы АМ и А1М1 равны, ВС=В1С1, ÐАМВ=ÐА1М1В1. На сторонах АС и А1С1 взяты точки К и К1 так, что АК=АК1. Найдите периметр DА1О1В1, если АО=5 см, В1О1=8 см, периметр DАВС=56 см.
Задача 2.4 расширяет задачу 2.2, а задачу 2.5 легко решить на основе решения задачи 2.3. Однако для решения обеих этих задач (4 и 5) от учащихся требуется знание уже второго признака равенства треугольников.
При изучении второго, а тем более третьего признака равенства треугольников, объем полученных учащимися знаний, умений и навыков возрастает. Вследствие этого, возможно увеличение длины задачных блоков, предназначенных для усвоения школьниками данных признаков. В таких блоках целесообразно предлагать учащимися задачи, решение которых будет способствовать формированию у них новых, ранее не выделяемых действий, адекватных методу, основанному на признаках равенства треугольников.
Например, выбирать из различных соотношений между сторонами и углами треугольников такие, которые наиболее просто доказать в ситуации выбора между двумя или тремя известными школьникам признаками равенства. Тогда при изучении учащимися второго признака им могут быть предложены, в частности, задачи, образующие следующий блок:
3.1. От вершины С равнобедренного треугольника АВС с основанием АВ отложены равные отрезки СК и СМ на сторонах СА и СВ соответственно. Верно ли, что ÐАКВ=ÐВМА?
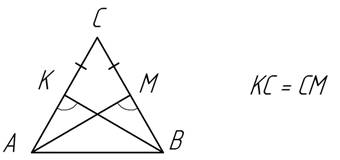
3.2. Точки М и Н, отмеченные на боковых сторонах равнобедренного треугольника АВС, отсекают равные отрезки ВМ и ВН. Отрезки АН и МС пересекаются в точке О. Докажите, что DАОВ=DСОВ.
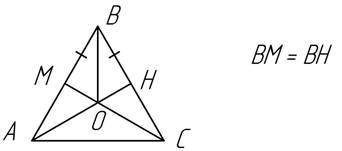
3.3. В равнобедренном треугольнике МРН с основанием МР на стороне МН отмечена точка М1, на стороне РН – точка Н1. Докажите, что DММ1С=DPH1С, где С – точка пересечения отрезков МН1 и РМ1 и если М1Н=Н1Н.
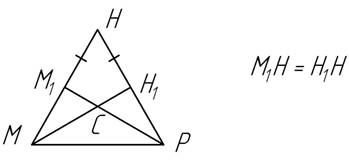
3.4. На боковых сторонах равнобедренного треугольника АМС с основанием МС отложены равные отрезки АР и АВ. Точка О – точка пересечения прямых МВ и РС. Докажите, что DСВМ=DМНР, где Н – точка пересечения прямых АО и МС.
3.5. Треугольник АВС – равнобедренный с основанием АС. На сторонах АВ и ВС отмечены точки А1 и С1 так, что А1В=ВС1. Отрезок А1С пересекает СА1 в точке О. Докажите, что треугольник А1С1М1 равнобедренный, где М1 – точка пересечения прямых ВО и АС.
Данный блок задач можно предложить учащимся и при изучении третьего признака равенства треугольников. Поскольку, начиная с задачи 5.2, после решения почти каждой из них можно поставить перед школьниками дополнительных вопрос: «Каким еще образом может быть доказано равенство этих треугольников?» Поиск ответа на него позволяет выделять различные способы решения одной и той же задачи, причем, возможно, с использованием уже всех трех признаков равенства.
Таким образом, сочетая методы решения геометрических задач в процессе решения взаимно обратных из них, одна задача может быть решена с помощью одного метода, а вторая с помощью другого.
Поэтому при обучении геометрии мы предлагаем постепенное прохождение основных этапов процесса формирования обобщенных приемов решения геометрических задач, а потому целесообразно подбирать циклы задач в соответствии с изложенными ранее этапами процесса их формирования.
Таким образом, каждый блок геометрических заданий может быть представлен в виде четырех блоков взаимосвязанных задач:
1) вспомогательные задачи, обеспечивающие актуализацию знаний, необходимых для решения рассматриваемого вида задач, а также формирование мотивации изучения обобщенных приемов их решения;
2) базисные задачи, предназначенные для выделения состава (образования) обобщенного приема решения каждого вида математических задач;
3) тренировочные задачи, предполагающие применение обобщенного приема к решению частных задач стандартного вида и обеспечивающие его усвоение;
4) развивающие задачи, ориентированные на перенос обобщенного приема, преобразование его состава при решении нестандартных математических задач.
Циклы задач, описанные выше, не являются неизменными. Они могут варьироваться в условиях различных направлений профилизации обучения. Как отмечалось ранее, в зависимости от выбранного направления в качестве приоритетных будут выступать различные цели обучения геометрии; в соответствии с ними будет доминировать реализация той или иной функции геометрических задач и достигаться различные уровни сформированности самих обобщенных приемов (задействоваться различные виды учебно-познавательной математической деятельности).
Готовые блоки геометрических задач также можно предлагать учащимся для домашней работы, или в качестве учебного материала для традиционных самостоятельных и контрольных работ, проведение которых сегодня остается основным способом контроля за уровнем знаний и умений учащихся. Варианты проведения таких самостоятельных и контрольных работ представлены в работе И.В.Ульяновой .
Обобщив вышеизложенное, выстроим последовательно методические условия, соответствующие этапам усвоения типового решения задач, через взаимосвязанные блоки:
1) создание ситуации, создающей потребность в введении учащимся изучаемого понятия (проблемная ситуация);
2) рассмотрение существенных и несущественных свойств объекта (описание объекта; построение геометрических чертежей; наблюдение за объектом в различным положениях, с различными метрическими характеристиками);
3) выделение нескольких простых существенных свойств (системой контрпримеров) и выделение из них определения;
4) решение простейших задач, направленных на переход от введенного определения к другим существенным свойствам (использование определения при решении задач);
5) определение часто повторяющихся существенных свойств и представление их в виде теорем (доказательство теорем);
6) рассмотрение теорем- «существенных свойств» в различных видовых группах понятия;
7) использование определения и теорем при решении задач (конструктивное усложнение задач).
Сложность решения блока геометрических задач, также как и сложность структуры решения задачи отождествляется со сложностью дерева. В качестве примера рассмотрим блок с целевой задачей - стыкование треугольников вершиной угла :
|
Задача №1
|
Дано: АО = ОС ВО = ОД Доказать: 1. Ð1 = Ð2 2. DАОВ = DСОД 3. а) АВ = СД б) Ð3 = Ð4 в) Ð5 = Ð6 4. Ð7 = Ð8 5. DАОД = DВОС 6. а) АД = ВС б) Ð9 = Ð10 в) Ð11 = Ð12 7. ÐА = ÐС 8. ÐВ = ÐД 9. DАВД = DСВД 10.DАСД = DАСВ
|
Таким образом, в методических исследованиях проблемы технологии проектирования блоков и обратных блоков геометрических задач имеются теоретические и практические предпосылки для формирования обобщенных умений учащихся по их решению, но они не конкретизированы на учебном предмете геометрия. Так, есть описание разработки компонентов технологических карт, дидактического модуля, но нет реализации проектирования технологии обучения геометрии при решении задач.
Задавая учащимся, блок задач, то есть, задавая набор упражнений, упорядоченных в соответствии с определенными целесообразными принципами, мы тем самым определяем систему действий обучаемых, намечаем структуру познавательного процесса. Таким образом, блок задач, во-первых, заключает в себе цель, поставленную учителем, и, во-вторых, еще и намечает структуру ее достижения. В связи с этим возникает проблема составления методически блоков взаимосвязанных задач.
Мы предлагаем использовать циклично-блочную организацию задач, предложенную С.В. Арюткиной. При этом если приѐм сообщается учащимся в готовом виде, то достаточно трѐх блоков задач, если же предполагается «открытие» приѐма, что само по себе очень важно для учащихся классов с углубленным изучением математики и геометрии, то необходимо четыре блока.
Первый блок задач (подготовительный) призван обеспечить мотивацию изучения приемов решения задач по геометрии и актуализацию необходимых для этого знаний. Для создания этого блока задач использован способ построения системы упражнений Г.И. Саранцева.
Задачи второго блока предназначены для раскрытия состава обобщѐнного приѐма и конструирования его на основе анализа и сравнения частных приѐмов (блок может быть опущен, если приѐм даѐтся в готовом виде). В основу построения этого блока задач положен принцип «от простого к сложному»: все задачи взаимосвязаны друг с другом и каждая последующая все более обобщает (усложняет) предыдущую.
С помощью третьего блока предполагается усвоение обобщѐнного приѐма при решении задач стандартного вида. Их решение предполагает использование всех действий из предыдущих задач блока.
Четвертый блок включает в себя нестандартные задачи, решение которых предполагает то или иное изменение обобщѐнного приѐма, что превращает его в гибкий инструмент умственной деятельности.
Таким образом, при составлении блоков взаимосвязанных задач по геометрии нужно руководствоваться следующим алгоритмом действий:
· постепенное усложнение материала;
· поэтапное увеличение объема работы;
· повышение уровня самостоятельности учащихся;
· интеграцию знаний и способов деятельности;
· привлечение элементов теории для решения познавательных задач;
· обучение способам рассуждения (как по образцу, так и самостоятельно) с учетом принципа вариативности задач;
· усложнение творческой направленности в выполнении заданий.
Охарактеризованный выше подход к созданию вариативных циклов задач по геометрии предполагает учет изменений в целях учебной деятельности по решению таких задач, доминирующих функций самих задач и способствует изменению степени самостоятельности школьников при их решении и выделении составов действий обобщенных приемов.
Список литературы
1. Калинкина Т.М. Динамические задачи как средство совершенствования процесса обучения геометрии в средней школе: Дис. ... канд. пед. наук. – Саранск, 1995. – 170 с.
2. Модонова М.В. Конструирование систем математических задач //Интеграция образования – 2009. – № 4. – С. 98-102
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.