Matematika darslarida o‘quvchilarni erkin fikrlashlarini rivojlantirish.

Matematika darslarida  o‘quvchilarni erkin fikrlashlarini  rivojlantirish.

Annotatsiya. Ushbu maqolada umumta'lim maktablarida sog'lom, komil insonlarni kamolga yetkizish bilan birga matematika fanini chuqur egallashi uchun yangi pedogogik va axborot texnologiyalaridan foydalanish orqali dars tashkil etish usullari yaqindan yordam berishi yoritilgan.

Kalit so‘z. Komil inson murakkab tenglama, funksiya, tensizlik, erkin fikr, progressiya.

         Insoniyat har davrda farzand tarbiyasi haqida qayg'urgan va tarbiyaning eng samarali tizimini topish uchun izlanganlar. Chunki sog'lom avlod jamiyat taraqqiyotini yuksaklarga ko`taradi. Shuning uchun komil  inson tarbiyasi hamisha muhim va dolzarb vazifa bo`lib kelgan. Prezidentimiz Islom Karimov  “Biz komil inson tarbiyasini davlat siyosatining ustivor sohasi deb ehlon qilganmiz” deb bejiz aytmagan.

Umumta’lim maktablari, kasb-xunar kollejlari, akademik litseylar va oliy o`quv yurtlarida o`qitiladigan matematika kurslaridan tashqari, darsdan bo`sh vaqtlarda tashkil etiladigan qo`shimcha mashg'ulotlar davomida amalga oshiriladigan ishlar matematika fani o`qituvchisidan ko`proq mehnat qilishni talab etadi. Jumladan, olimpiadaga tayyorgarlik ko`rish va uni o`tkazish  ҳamda oliy o`quv yurtlariga kiruvchilar uchun tanlanadigan misol va masalalarning umumiy ko`rinishi, yechilishi bilim va tafakkurni talab etadi. Ushbuni xisobga olgan xolda, quyida murakkabroq bo`lgan misol masalalarni yechilish yo`llaridan namunalar keltirib o`tamiz.

 1  variant

1.  Ifodani soddalashtiring:

 Yechish:  

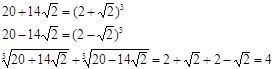
2. Tenglamani butun sonlarda yeching   

Yechish: Berilgan tenglama  ga teng kuchli.

                                                                        J:  (1;10), (4; 4), (0;-4), (-3;2)

3.    funksiyaning  grafigini chizing.

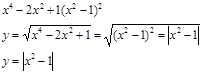
4.  Ko`paytuvchilarga ajrating:

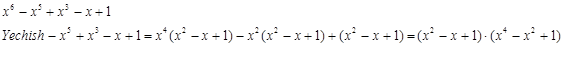
5. Uchburchakning  va  tomonlari  arifmetik progressiya tashkil qiladi.   bo'lishini isbotlang. Bu yerda  va  mos xolda tashqi va ichki chizilgan aylanalarning radiuslari. 

Yechish:

2  variant

1.   ni  isbotlang.

Isbot.   

2.  Kuyidagi tenglikni qanoatlantiradigan barcha butun x,u larni  toping.

               6x + u = 2xu - 4

Echish:

           J: (1;10),(4;4), (0;-4), (-3;2)

3. Ifodani  soddalashtiring:

Echish:

4. Xisoblang: 

Echish: CHeksiz kamayuvchi geometriya progressiyaning yig'indisini topish formulasidan foydalanib, berilgan ifodani quyidagicha yozamiz:

.

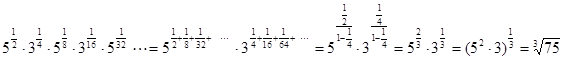           5. a,v,s- ixtiyoriy uchburchak tomonlarining uzunliklari bo`lsa,

 tengsizlik urinli  ekanligini isbolang.

   V

                                                        Isbot.

     A    s    a

          V               S              Bu ikkala tengsizlikdan ularni qo`shib

                                            quyidagini olamiz:

Ushbu keltirilgandan ko`rinib turibdiki, har bir topshiriq o`quvchilarni ijodiy ishlashga jalb etish bilan birga mustaqil bilimlarini ro`yobga chiqarishga hamda uni mustahkamlashga chorlaydi.

Umumta’lim maktablarining 7-9 sinflari  algebra kursi uchun o`quvchilarini    egallashlari majbur bo`lgan davlat ta’lim  standarti asosida tuzilgan tayanch o`quv rejasi  bo`yicha, muammoga sabab bo`layotgan ayrim mavzularga ehtiborni qarataylik.

Matematika fanini o`qitishda yangi pedagogik va axborot texnologiyalaridan foydalanish orqali dars tashkil etish usullari  yaqindan yordam beradi.

Jumladan, chiziqli funksiya va uning xossalari va kvadrat funksiya  mavzularini  o`qituvchi o`qitish jarayonida bir qatror muammolarga duch kelmoqda, ularni bartaraf etish maqsadida, quyidagicha metodik tavsiya taqdim etamiz.  Har bir nomanfiy x songa  sonni mos  qo`yadigan funksiya, yahni  funksiyani qaraylik. Bu funksiya uchun argument faqat  nomanfiy qiymatlarni qabul  qilishi mumkin:  x. Bu xolda funksiya barcha nomanfiy sonlar to`plamida aniqlangan deyiladi va  bu  esa, u= funksiyaning aniqlanish sohasi deyiladi.

Funksiyaning aniqlanish sohasi deb, uning argumenti qabul qilishi mumkin bo`lgan barcha qiymatlariga  aytiladi.

   Misol:  1) u =  formula bilan berilgan funksiya   x da  aniqlangan, yahni  bu funksiyaning  aniqlanish sohasi – noldan farqli  barcha xaqiqiy  sonlardan iborat bo`ladi.

    2)  Tekis  harakat formulasi S=v va  argument t ning qabul qilishi  mumkin bo`lgan qiymatlar sohasi t  dan iborat. Ko`pburchak ichki burchaklarining yig'indisi   formula buyicha xisoblanadi, bunda n-ko`pburchak tomonlarining soni – argument. Argumentning qabul qilishi mumkin bo`lgan qiymatlari 3, 4, 5, 6, ... sonlar, yahni bu funksiyaning aniqlanish sohasi, 3 dan kichik bo`lmagan natural sonlardan iborat.  

       Funksiyaning o`zgarish  sohasi deb, funksiya qabul qilishi mumkin bo`lgan barcha qiymatlarga aytiladi.

   Misol:   1).  u=x funksiyaning o`zgarish sohasini toping.

   Yyechilishi. Demak, funksiyaning o`zgarish sohasi - dan katta yoki  ga teng barcha  sonlardan  iborat, chunki                        (x- (nomanfiy son). Tengsizlik  yordamida  buni  shunday yozish mumkin:  yoki

       Agar f(x) funksiyaning qiymati x=a da nolga teng bo`lsa, u xolda a soni  shu funksiyani ildizi deyiladi.

       F(x)  funksiyaning ildizini topish uchun uni  nolga tenglab, xosil bo`lgan  f(x)=0  tenglamni yechish kerak.

  Masalan, f(x)=5x² –3x-8 funksiyani  ildizlari 5x² –3x-8=0 tenglamaning  ildizlaridan iborat:        x₁=  x₂=.

       Funksiyaning grafigi deb, koordinatalar  tekisligining  abtsissalari shu funksiyaning  aniqlanish sohasidan olingan erksiz o`zgaruvchining qiymatlariga, ordinatalari esa  funksiyaning unga mos qiymatlariga teng bo`lgan  nuqtalariga aytiladi.

    Misol. u= funksiyaning grafigini yasang.

    Yyechilishi.  funtsiyaning grafigi u= funksiya grafigidan uni OX o`q bo`yicha 3 birlik o`ngga surish bilan hosil qilinadi.

 funksiyaning grafigini   hosil qilish uchun  funksiyaning grafigini 2 birlik pastga surish yetarli.   Agar f(x) funksiya argumentning ishorasi o`zgarganda o`z qiymatini o`zgartirmasa, yahni funksiya f(-x)=f(x) shartini qanoatlantirsa, bunday funksiya juft funksiya deyiladi.

    Masalan, f(x)=x²- juft funksiya, chunki f(x)=(-x)² =x

    Agar  u=f(x) funksiya argumentining ishorasi  o`zgarganda o`z qiymatini qarama-qarshi  qiymatga  o`zgartirsa, yahni f(-x)=-f(x)  shartni qanoatlantirsa, bunday funksiya tok funksiya deyiladi.

    Masalan, f(x)=sinx – toq funksiya, chunki f(-x)=-sin(-x)=-f(-x)

    Agar argumentning biror oraliqdan olingan  katta qiymatiga funksiyaning katta qiymati mos kelsa, yahni shu oraliqqa tegishli istalgan x_1;x₂ lar uchun

x₂ >x₁  tengsizlikdan u(x₂)>u(x₁) tengsizlik kelib chiqsa, u(x)  funksiya  shu  oralikda o`suvchi funksiya  deyiladi.

    Agar biror oraliqqa tegishli istalgan x_1;x₂ lar uchun x₂ >x₁ tengsizlikdan u(x₂)>u(x₁) kelib chiqilsa, u(x) funksiya  shu oraliqda kamayuvchi funksiya deyiladi.  Masalan, u=3x+4-sonlar o`qining hamma  yerida o`suvchi funksiya  u=x² funksiya x oraliqda o`sadi, xoraliqda  kamayadi. u=funksiya, yahni u=x funksiya x>0 oraliqda kamayadi.

O`suvchi va kamayuvchi funksiyalar monoton funksiyalar deyiladi.

Funksiyaning o`sishi geometrik jihatdan shuni  bildiradiki,  o`suvchi funksiyaning grafigi bo`yicha chapdan o`ngga qarab harakatlanayotgan nuqta  pastdan yuqoriga ko`tariladi, kamayuvchi funksiyaning grafigi bo`yicha (chapdan o`ngga) harakatlanayotgan nuqta esa yuqoridan pastga tushadi.

     Misol. 1)  u= funksiyaning grafigini yasang.

Yechilishi. , yahni u=- shakliga keltirildi.u=- funksiya grafigini OX o`q bo`yicha  o`ngga bir birlik va OY o`q bo`yicha ikki  birlik yuqoriga surish  bilan u=-  funksiyaning grafigini xosil qilish mumkin.

       Misol. 2)  funksiyaning aniqlanish sohasini toping.

Yechilishi. Ildiz ostidagi ifodalar nomanfiyligi sababli 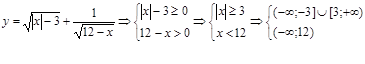            Javob:  D(u)= 

Misol. 3). funksiyaning aniqlanish sohasini toping.

       funksiyadan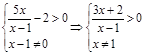        

                      Javob:      

Foydalanilgan adabiyotlar ro`yxati.

1.            M.Axadova “O`rta Osiyolik mashhur olimlar va ularning matematikaga oid ishlari”        O`qituvchi-1983 y.        

2.            Yo.Saitov “Matematika va matematiklar haqida” O`qituvchi-1992 y.

3.            A.Abduraxmonov “Al Xorazmiy buyuk matematik”      O`qituvchi-1983 y.

4.            M.Xayrullaev “Mantiq” O`qituvchi-1993 y.

5.            O`zbekiston Respublikasi Prezidentining 2004 yil 21 may PF-3431 raqamli  Farmoni.

6.            O`zbekiston Respublikasi  Vazirlar Mahkamasining 2004 yil iyuldagi

7.            321-raqamli  Qarori.

8.            O`zbekiston Respublikasining “Ta’lim to`ғrisida”gi Qonuni, “Kadrlar tayyorlash milliy dasturi”.

9.            O`zbekiston Respublikasi XTBning 2005 yil 10 noyabrdagi 35-sonli Hay’at qarori.

10.        Xalq ta’limi Vazirligining 2006 yil 7 iyundagi «Pedagog kadrlarni qayta tayyorlash va malakasini oshirish tizimini yanada takomillashtirish to`ғrisida»gi 149-sonli buyruғi.

11.        J.G'.Yo`ldoshev, S.A.Usmonov «Pedagogik texnologiya asoslari» Toshkent, O`qituvchi 2004 y.

12.        A.A’zamov A.Yusupov «O`quvchilarga bilim berishda» innovatsion usullardan foydalanish Toshkent-2002 yil.