ÓÄÊ 373.167.1:51

ÁÁÊ 22.1ÿ721 Ì 30

Ìàð÷åíêîÈ.Ñ.

Ì 30                                        Ìàòåìàòèêà:1—4êëàññû:âñõåìàõèòàáëèöàõ/È.Ñ.Ìàð÷åíêî.—Ì.:

Ýêñìî,2011.—144ñ.—(Íàãëÿäíîèäîñòóïíî.Íà÷àëüíàÿøêîëà).

ISBN 978-5-699-46303-9

Âèçäàíèèâñæàòîé,êîíöåíòðèðîâàííîéôîðìåïðèâîäèòñÿîñíîâíîéòåîðåòè÷åñêèé ìàòåðèàë,îõâàòûâàþùèéêóðñìàòåìàòèêèíà÷àëüíîéøêîëû.Ïðàâèëà,îïðåäåëåíèÿîáúåäèíåíû â íàãëÿäíûå ëîãè÷åñêèå áëîêè, ñõåìû, êîòîðûå ïîçâîëÿþò ëó÷øå ïîíÿòü è óñâîèòü

èíôîðìàöèþ.

Ïîñîáèå îêàæåò íåîöåíèìóþ ïîìîùü â ó÷åáå, ñèñòåìàòèçèðóÿ ïîëó÷åííûå çíàíèÿ, à òàêæå áóäåò ïîëåçíûì ïðè ïîäãîòîâêå ê èòîãîâîìó òåñòèðîâàíèþ ïî ìàòåìàòèêå çà êóðñ

íà÷àëüíîé øêîëû.

ÓÄÊ373.167.1:51 ÁÁÊ22.1ÿ721

©Ìàð÷åíêîÈ.Ñ.,2010

ISBN 978-5-699-46303-9                                                                   ©OOΫÈçäàòåëüñòâî«Ýêñìî»,2011

Содержание

Числа и цифры............................................................................ 7

Натуральные числа..................................................................... 7

Разряды и классы натуральных чисел . . . . . . . . . . . . . . . . .8 Сравнение чисел . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 Сложение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 Таблица сложения натуральных чисел 

в пределах 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

3              Таблица сложения натуральных чисел

в пределах 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 Вычитание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 Состав числа (первый десяток) . . . . . . . . . . . . . . . . . . . . . . 17 Законы сложения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Сложение и вычитание с переходом

через десяток . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 Сложение и вычитание двузначных чисел

без перехода через десяток . . . . . . . . . . . . . . . . . . . . . . . . . 20 Вычитание однозначного числа 

из разрядных десятков, сотен . . . . . . . . . . . . . . . . . . . . . . . 20

8 Вычитание двузначного числа

из круглого двузначного . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

Вычитание двузначных чисел с переходом через десяток . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 Письменное сложение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

Письменное вычитание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 Проверка сложения и вычитания . . . . . . . . . . . . . . . . . . . 30 Умножение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 Деление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Законы умножения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

Свойства деления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 Нахождение компонентов деления . . . . . . . . . . . . . . . . . . 39 Таблица умножения и деления . . . . . . . . . . . . . . . . . . . . . . 40

Таблица умножения Пифагора . . . . . . . . . . . . . . . . . . . . . . . 44

Особые случаи умножения . . . . . . . . . . . . . . . . . . . . . . . . . . 44

0          Особые случаи деления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45

Умножение на 10, 100, 1000 . . . . . . . . . . . . . . . . . . . . . . . . . 45 Умножение круглого числа 

на однозначное . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

Устное умножение двузначных 

и трёхзначных чисел на однозначное число . . . . . . . 47 Письменное умножение многозначного числа на однозначное (в столбик) . . . . . . . . . . . . . . . . . . . . . . . . . . 48 Умножение многозначного числа на двузначное, трёхзначное и т. д. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 Умножение чисел с нулём на конце . . . . . . . . . . . . . . . . 50 Умножение многозначного числа

на многозначное число с нулём в середине . . . . . . . 51

Деление на 10, 100, 1000 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

Деление круглых чисел . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 3

Деление двузначного числа на двузначное . . . . . . . . . 53 Деление с остатком . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

Письменное деление на однозначное число 

(деление в столбик) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 Примеры письменного деления . . . . . . . . . . . . . . . . . . . . . 57

Деление многозначного числа на круглое . . . . . . . . . . 60 Случаи деления на однозначное число,

когда 0 в середине частного . . . . . . . . . . . . . . . . . . . . . . . . 62 Деление многозначного числа на двузначное . . . . . . 63

Деление многозначного числа на трёхзначное . . . . . 66

        Проверка деления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68               8

Признаки делимости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 Именованные числа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 Преобразования именованных чисел . . . . . . . . . . . . . . . 71

Сложение и вычитание именованных чисел . . . . . . . . 73

Умножение и деление именованных чисел . . . . . . . . . 74 Выражения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 Порядок действий в выражениях . . . . . . . . . . . . . . . . . . . . 76 Равенства и неравенства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 Уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 Решение простейших уравнений . . . . . . . . . . . . . . . . . . . . 80 Учимся решать задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

Задачи на нахождение суммы двух чисел . . . . . . . . . . 84 Задачи на нахождение остатка . . . . . . . . . . . . . . . . . . . . . . 86

Задачи на увеличение числа 

на несколько единиц . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 0 Задачи на уменьшение числа

на несколько единиц . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 Задачи на разностное сравнение двух чисел . . . . . . . 89 Задачи на нахождение неизвестного слагаемого . . . 90 Задачи на нахождение неизвестного

уменьшаемого . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90 Задачи на нахождение неизвестного вычитаемого . . 91 Задачи на нахождение произведения двух чисел . . 92 Задачи на нахождение частного двух чисел . . . . . . . . 93

Задачи на увеличение числа в несколько раз . . . . . . 94 Задачи на уменьшение числа в несколько раз . . . . . 95 Задачи на кратное сравнение двух чисел . . . . . . . . . . . 96

Задачи на нахождение неизвестного множителя . . . 96

3            Задачи в косвенной форме . . . . . . . . . . . . . . . . . . . . . . . . . . 98

Обратные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101

Цена, количество, стоимость . . . . . . . . . . . . . . . . . . . . . . . . 103

Составные задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104 Задачи на приведение к единице . . . . . . . . . . . . . . . . . . 106 Усложнённые задачи на приведение к единице . . . 107 Задачи на нахождение слагаемого

и вычитаемого . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 Задачи на нахождение суммы

двух произведений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 Составные задачи на совместную работу . . . . . . . . . . 111

8 Составные задачи на зависимость между

величинами «цена», «количество», «стоимость» . . . . 113 Задачи на пропорциональное деление . . . . . . . . . . . . . 114 Задачи на движение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115 Задачи на встречное движение . . . . . . . . . . . . . . . . . . . . . 118 Задачи на движение в противоположных

направлениях . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121

Задачи на движение в одном направлении . . . . . . . . 123 Дроби . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125 Сравнение дробей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 Простые задачи на нахождение части от числа . . . 127 Простые задачи на нахождение числа

по его части . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128 Составные задачи на нахождение части

от числа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128

0              Составные задачи на нахождение числа

по его части . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129 Основы геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130 Задачи по геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138

Математика

Числа и цифры

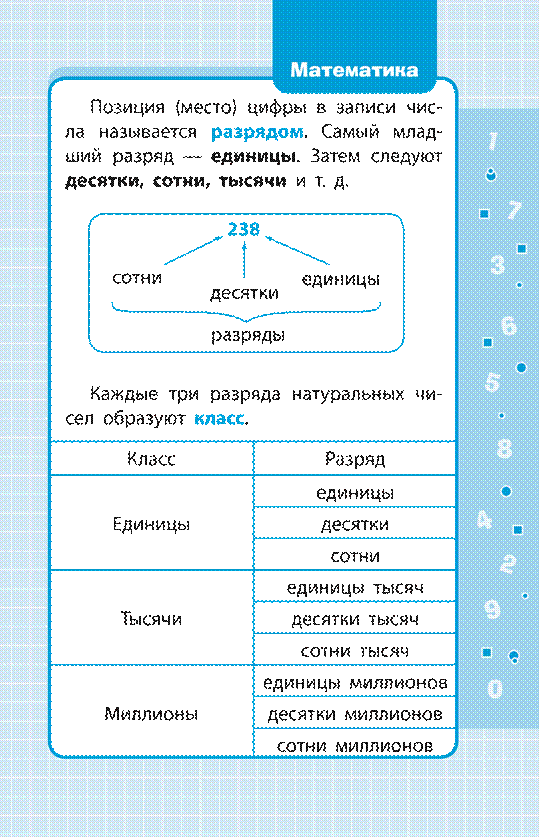
Числа — это единицы счёта. С помо­

щью чисел можно сосчитать количество предме тов и определить различные величины (длину, ширину, высоту и т. д.).

Для записи чисел используются специ­ 3 альные знаки — цифры. Цифр десять:

1 2 3 4 5 6 7 8 9 0

Натуральные числа

Числа, которые используются при счё­       8 те, называются натуральными.

1, 2, 3, 4, 5, 6, 7, 8, 9, 

10, 11, 12, 13, 14, 15, 16, 

17, 18, 19, 20, …,

1 — самое маленькое число.

 — самого большого числа не существует.

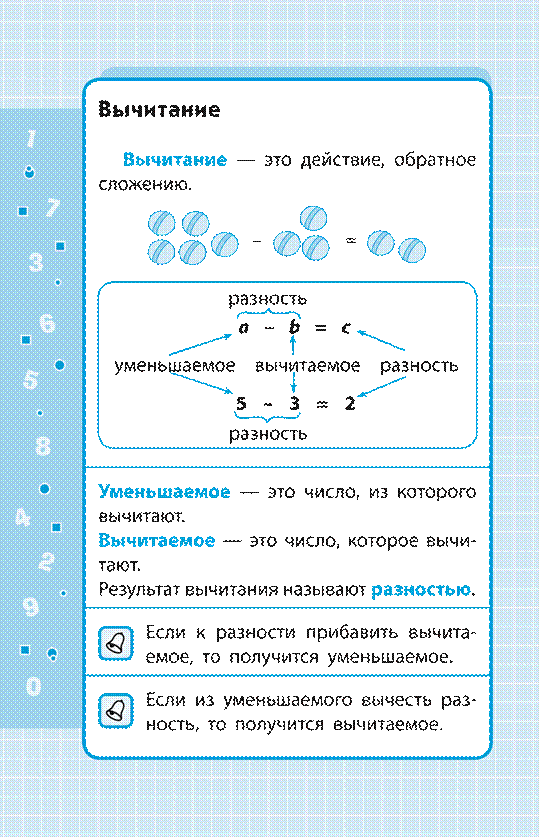
Число 0 (нуль) обозначает отсутствие

             предмета.                                                                      0

Нуль не является натуральным числом.

Математика

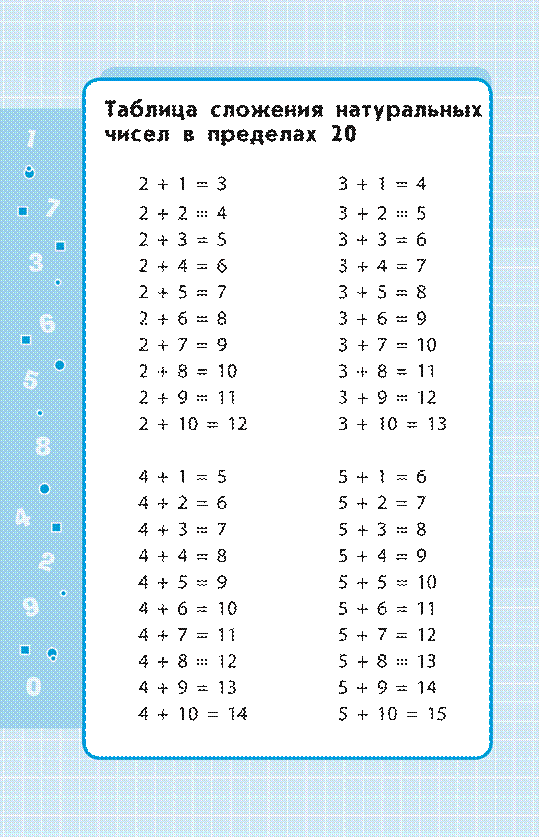
Как нужно рассуждать, решая пример  13 – 5?

Число 5 удобно представить в виде суммы чисел 3 и 2. Вычитаем число 5 частями. Сначала из 13 вычитаем 3. Получится 10. Затем из 10 вычитаем 2. По­

              лучится 8.                                                                      3

13−5 =13−3−2 =10 −2 = 8

                                    3          2

 Сложение и вычитание частями  Чтобы прибавить или вычесть чис­

                              ло частями, нужно:                                            8

1.     Представить это число в виде суммы удобных или разрядных слагаемых.

2.     По очереди прибавить или вычесть эти слагаемые. Например:

17 + 5 = 17 + 3 + 2 = 20 + 2 = 22

23 – 15 = 23 – 13 – 2 = 10 – 2 = 8

                                                                       или                                              0

23 – 15 = 23 – 10 – 5 = 13 – 5 =  13 – 3 – 2 = 8

Математика

2) Вычитаем единицы из 10 и результат прибавляем к первому слагаемому:

30 – 8 = (20 + 10) – 8 = 

= 20 + (10 – 8) = 20 + 2 = 22

Вычитание двузначного числа

                     из круглого двузначного                               3

 40 – 24

1)    Представляем 24 в виде суммы разрядных слагаемых:

24 = 20 + 4

2)    Сначала из 40 вычитаем 20, а затем из

                        полученной разности вычитаем 4:                      8

40 – 24 = 40 – (20 + 4) = 

= (40 – 20) – 4 = 20 – 4 = 16

Вычитание двузначных чисел с переходом через десяток

1.     Представляем уменьшаемое в виде сум ­

                       мы удобных слагаемых.                                        0

2.     Представляем вычитаемое в виде суммы разрядных слагаемых.

В столбик можно складывать  несколько слагаемых. При этом знак «+» ставится один раз.

                                           483 + 6 201 + 78 994                     ₁₁

                                      Удобнее всего первым за­        +78994

3 писать то число, в котором больше разрядов. 6201

Письменное вычитание

1. Записываем вычитаемое под уменьша­

8               емым: единицы под единицами, десятки под десятками.

2.     Вычитание начинаем с единиц.

 Проверяем, возможно ли из единиц уменьшаемого вычесть единицы вычитаемого. Если нет, то занимаем 1 десяток (10 единиц) из десятков уменьшаемого. Ставим над десят ка ми точку, чтобы об этом не забыть.

3.     Вычитаем единицы.

0             4. Вычитаем десятки.

5. Читаем ответ.

Математика

 8 204 – 4 397

1)    Записываем вычитаемое под g уменьшаемым: единицы под −₈₂₀₄^{g g10} единицами, десятки под де­ 4397 сятками, сотни под сотнями, 3807 тысячи под тысячами.

2)    Вычитаем единицы: из 4 нельзя вы­ 3 честь 7. Занять у десятков нельзя, поэтому занимаем 1 сотню (10 десятков). 1 десяток берём для единиц, остаёт­ ся 9 десятков:

10 + 4 = 14 14 – 7 = 7

8

                   Записываем 7 под единицами.

3)    Вычитаем десятки: из 9 десятков, которые заняли у сотен, вычитаем 9 десятков:

9 дес. – 9 дес. = 0 дес.

                   Записываем 0 под десятками.

4)    Вычитаем сотни: было 2 сотни, 1 сотню заняли, осталась 1 сотня. Из 1 сотни вычесть 3 сотни нельзя. Занимаем 0

1 тысячу (10 сотен):

Законы умножения

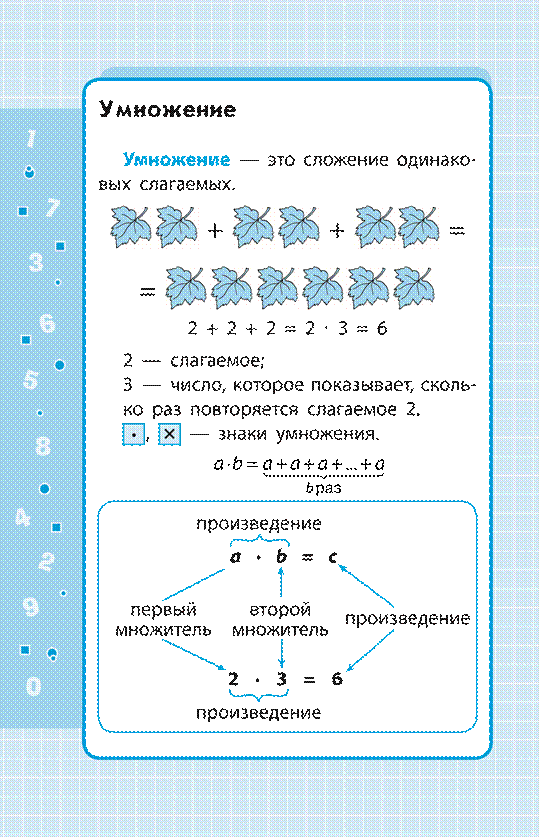
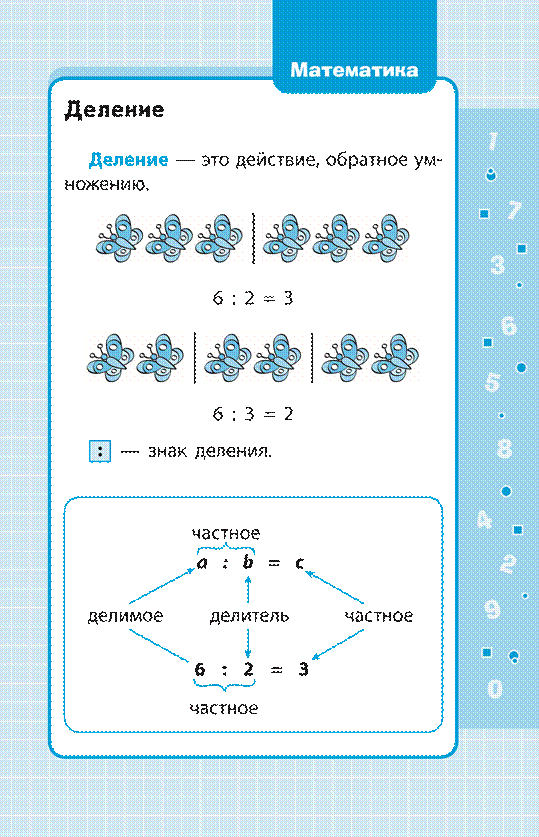
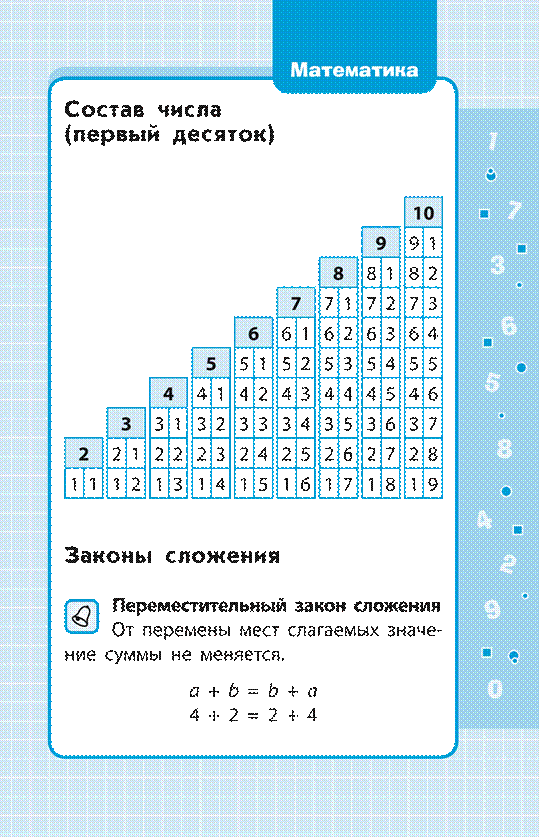
Переместительный закон умножения

От перестановки множителей произведение не меняется.

³                                2a  _∙∙ 5 = 5  b = b ∙_∙  2a

10 = 10

 Сочетательный закон умножения

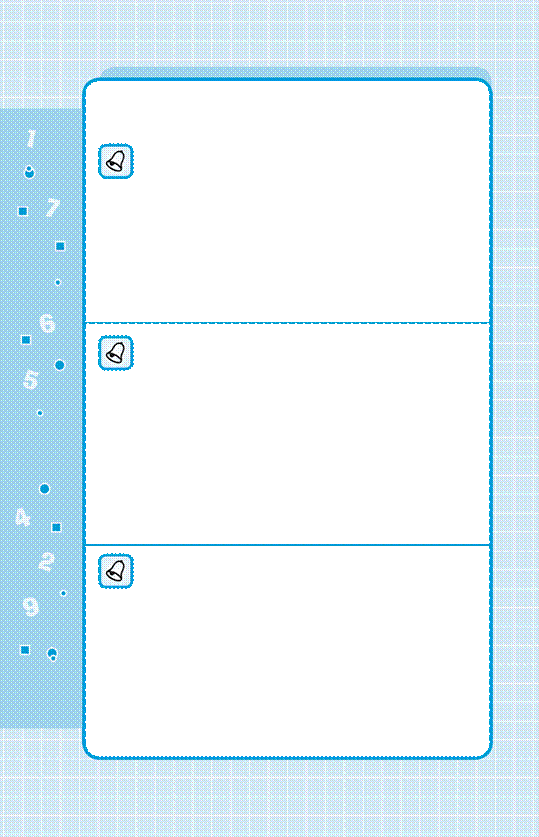Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение 8 второго и третьего чисел.

(a ∙ b) ∙ c = a ∙ (b ∙ c) = (a ∙ c) ∙ b (2 ∙ 5) ∙ 3 = 2 ∙ (5 ∙ 3) = (2 ∙ 3) ∙ 5

                                              30                        30                            30

Распределительный закон умножения

Относительно сложения

Произведение суммы на число равно сумме произведений каждого слагаемого

0             на это число.

(a + b + c) ∙ d = a ∙ d + b ∙ d + c ∙ d

(2 + 5 + 3) ∙ 2 = 2 ∙ 2 + 5 ∙ 2 + 3 ∙ 2 = 20

Письменное умножение многозначного числа 

на однозначное (в столбик)

Умножение многозначного числа на однозначное можно выполнить в столбик.

3 _{писывается многозначный множитель, а} При умножении в столбик сначала запод ним — однозначный. Слева ставится знак умножения × . Результат умножения (произведение) записывается под чертой.

327 ∙ 3

1) Записываем однозначное чис­

8               ло 3 под разрядом единиц          _×327² числа 327.         3

2)     Умножаем единицы: 7 ∙ 3 = 981 = 21, единицу пишем под единицами, 2 десятка запоминаем.

3)     Умножаем десятки: 2 ∙ 3 = 6, и ещё 2 десятка, которые запоминали. Получается 8 десятков. Пишем 8 под десят­

ками.

0 4) Умножаем сотни: 3 ем 9 сотен под сотнями.∙ 3 = 9. Записыва­

5) Читаем ответ: произведение равно 981.

Умножение чисел с нулём на конце

 7 280 ∙ 4 900

1) Записываем множите­ 13 ли один под другим так, 27

3                 чтобы     нули     остались     × 72804900

в стороне. Действие с ну­      6552 лями не производится.        + 2912 В конце умножения нули         35672000

просто сносятся в про­ изведение.

2) Находим первое неполное произведе­

8 ние: 728 чинаем под той цифрой, на которую ∙ 9 = 6 552. Подписывать на­

умножаем (то есть под 9).

3)     Находим второе неполное произведение: 728 ∙ 4 = 2 912. Подписывать начинаем под 4.

4)     Складываем неполные произведения.

5)     Считаем количество нулей в обоих множителях (три нуля) и дописываем их справа к произведению.

0             6) Читаем     ответ:     произведение    равно

35 672 000.

Математика

Умножение многозначного числа на многозначное число с нулём в середине

 247 ∙ 602

1)    Записываем множители так, 4 чтобы единицы были под ^×247602²¹ 3

единицами,     десятки      под десятками, сотни под сот­     + нями и т. д.

2)    Находим первое неполное 148694 произведение: 247 ∙ 2 = 494

8

3)    В разряде десятков числа 602 стоит 0. При умножении на 0 в результате получится 0, поэтому это действие пропускаем.

4)    Находим второе неполное произведение:          247 ∙ 6       =        1 482       и        начинаем подписывать его под тем числом, на которое умножаем (то есть под сотнями).

5)    Складываем неполные произведения.

6)    Читаем   ответ:         произведение    равно 0

148 694.

2-й способ

 Чтобы делать меньше проб при подборе числа, нужно обратить внимание на последнюю цифру в делимом (81) и делителе (27). Затем в таблице на 7 (это последняя цифра в делителе) най­

3 ти такое число, которое оканчивается _{цифрой 1 (это последняя цифра в де­}

лимом). Это число 21. Чтобы получить 21, нужно 7 умножить на 3. Это пробное число. Нужно сделать проверку умножением:

27 ∙ 3 = 81

8                   Значит, частное найдено верно.

Деление с остатком

Не всегда одно число можно разделить на другое целиком.

В таких случаях числа делят с остатком. Остаток всегда меньше делителя.

0                                                                  

5 : 2 = 2 (ост. 1),  1 < 2

Письменное деление на однозначное число 

(деление в столбик)

Порядок деления

1. Прочитай и запиши пример.

3              2. Выдели первое неполное делимое.

3.     Определи высший разряд и количество цифр в частном.

4.     Выполни деление, чтобы найти первую цифру в частном.

5.     Выполни умножение, чтобы опреде8 лить, сколько единиц высшего разряда осталось разделить.

6.     Проверь, правильно ли подобрана цифра в частном.

7.     Если получился остаток, запиши его в единицах нижнего (следующего) разряда и прибавь единицы того же разряда делимого (если они есть).

0 8. Продолжай деление, пока не выпол­нишь его до конца.

9. Проверь результат.

Математика

Примеры  письменного деления

1)     Определяем первое непол­ 459 : 3  459)  3

           ное делимое. Это 4 сотни.                 ^...

2)     Определяем количество цифр в част­ 3 ном. Их будет три: сотни, десятки, единицы.

3)     Делим первое неполное −3459 13.. делимое 4 на 3; ближайшее меньшее число 3 (оно 1 делится на 3 без остатка):

3 : 3 = 1. Цифра 1 — первая цифра в частном. Из 4 вычитаем 3, находим 8 остаток 1. Проверяем: остаток меньше делимого, 1 < 3.

4)     Сносим следующую цифру — 5. Второе неполное −3⁴⁵⁹ 15³ .

делимое (15) делим на 3. Оно делится без остатка: −¹⁵15 15 : 3 = 5. Пишем цифру 5 в частном. Находим остаток: 15 – 15 = 0, нуль не пишем.

5)     Сносим последнюю цифру — 9. Де­ 0 лим 9 на 3. Получилось 3. Записываем

 цифру 3 в частном и на­ − 3459 1533 ходим остаток: 9 – 9 = 0. Остатка нет. Число поде­

                     лилось полностью.                  −

6)     Читаем ответ: частное равно 153.    −9

3

В некоторых случаях первое неполное делимое — двузначное число.

 258 : 3

1) Определяем первое непол­ное делимое. 2 на 3 разде­      ²⁵º_{8 3..}

8            лить нельзя, поэтому берём

две цифры делимого — 25. Это и есть первое неполное делимое.

2)     Определяем количество цифр в частном. Их будет две: десятки и единицы.

3)     Делим первое неполное де­

лимое 25 на 3. Ближайшее наименьшее число, которое         −258 83.

делится на 3 без остатка, —

0 24. 24в частном первую цифру : 3 = 8. Записываем  — 8. Из 25 вычитаем 24, находим остаток 1.

Математика

2. Деление многозначного числа на круглое без остатка.

 12 750 : 30

1)     Определяем первое не­ 127»50 30 полное делимое — 127. ...

2)     Определяем количество 3 цифр в частном. Их будет три.

3)     Числа 127 и 30 делим на 10. 12 : 3 = 4. Записываем 4 в частном.

Умножаем 4 на 30. По­лучилось 120. Находим −127»50 ³⁰4.. остаток: 127 – 120 = 7.

           Остаток 7 < 30.                                                        8

4)     Сносим следующую цифру (5) и записываем рядом с остатком. Второе неполное делимое — 75.

5)     Делим 75 и 30 на 10, за­ ⁻127120»50 4230. тем 7 делим на 3. Получилось 2. Записываем 2 75 в частном. Умножаем 2 − 60

           на 30. Получилось 60.                  15

     Находим остаток:                                                    0

75 – 60 = 15. Остаток 15 < 30.

6)     Сносим последнюю циф­ −12012750 42530 ру (0) и запи сываем ря­

дом с остатком. Третье 75 не полное делимое — − 60

                       150. 150 и 30 делим на           −

10, а затем 15 делим на

3    3Записываем 5 в част. Полу чилось 5.    ­

ном. 30 ∙ 5 = 150. Остатка нет.

7) Читаем ответ: частное равно 425.

Случаи деления на  однозначное число, когда 0 

8 в середине частного

24 320 : 4

1)     Определяем      первое       не­    24º320 ⁴

                    полное дели мое.                                  ^....

2)     Определяем количество цифр в частном. Их будет четыре: тысячи, сотни, десятки, единицы.

3)     Делим 24 на 4. Получи­ −₂₄24º320 46... лось 6. Находим оста­

0           ток: 24 – 24 = 0. Остатка              3

нет.

Математика

4)     Сносим следующую циф­ º320 4 ру — 3. Число 3 на 4 −2424 60..

не делится. Записываем 32 в частном 0.

5)     Сносим следующую циф ­ ру — 2 и запи сываем −2424320 60804

её после цифры 3. По­    3 лучилось         число         32. Делим 32 на 4. Получилось 8. Находим остаток: 32 – 32 = 0. Остатка нет.

6)     Последняя цифра делимого 0, переносим её в частное. 7) Читаем ответ: частное равно 6 080.

8

Деление многозначного числа  на двузначное

1. Деление          без    остатка   трёхзначного чис ла на двузначное, если в частном получается однозначное число.

                 315 : 63                               −³¹⁵315^{¼ 63}5

1)     Чтобы найти цифру в част­  0        0 ном,       заменяем делитель

ближайшим круглым числом. Это число 60.

2)     Делим 315 на 60. Для этого достаточно разделить 31 на 6. Пробная цифра 5.

3)     Умножаем 63 на 5 (устно). Получаем 315. Значит, цифра 5 подходит.

3       4) Читаем ответ: частное равно 5.

Если при делении на двузначное число в частном получается одна цифра (однозначное число), то её можно найти методом подбора. Для этого нужно посмотреть на последнюю цифру в делителе и делимом и, пользуясь таблицей 8 умножения, подобрать цифру в частном.

2. Деление без остатка многозначного числа на двузначное, если в частном получается многозначное число.

27 904 : 64

1)     Определяем первое неполное делимое — 279.

2)     Определяем      количество

0 цифр в частном. Их будет ^{279¼04 64}... три: сотни, десятки, единицы.

Математика

3)     Чтобы найти первую цифру в частном, нужно делимое 279 и делитель 64 разделить на 10, то есть закрыть по одной цифре справа. Делим 27 на 6. Ближайшее число, которое делится на 6, — 24.

 Делим 24 на 6. Получилось 4. Это пробное число.

4)     Проверяем пробное число 4: 3

       64 ∙ 4 = 256.

5)     Вычитаем число 256 из   −256279¼04 644..

279. Остаток — 23, 23 <

< 64. Значит, цифра 4 23 подобрана верно.

6)     Сносим следующую цифру (0) и запи­

сываем её рядом с остатком. Получи­лось число 230. Это второе неполное     8 делимое.

7)     Делим 230 на 64. Закрываем в делимом и делителе по одной цифре справа: 23 : 6. Берём по 3. Проверяем цифру 3. Умножаем 64 на 3. Получилось 192. Находим остаток: 230 – 192.

8)     Получилось 38.Сравниваем    остаток      и       −256279¼04 4364.

делитель. Остаток мень­ше. Значит, цифра 3 −230 0 подобрана верно.

9)     Сносим следующую цифру (4) и записываем рядом с остатком 38. Это число 384. Третье неполное делимое — 384.

10)           Определяем послед­ −256^279¼04 43664 нюю цифру в част ном

3 по делителя. последней В      таблице цифре       −192230

умножения на 4 нахо­ 384 дим число, которое при −384 умножении на 4 окан­ 0 чивается цифрой 4.

Это число 6. Проверяем: 64 ∙ 6 = = 384. Находим остаток: 384 – 384 = 0.

8          Деление закончено.

11) Читаем ответ: частное равно 436.

Деление многозначного числа  на трёхзначное

 37 294 : 643

1) Определяем первое  3729¼4 643 неполное дели  мое — ..

0         3 729.

2) Определяем количество цифр в частном. Их будет две: десятки и единицы.

Математика

3)     Чтобы 3 729 разделить на 643, достаточно 37 разделить на 6. Берём по 6.

4)     Проверяем цифру 6 : 64 ∙ 6 = 384. Это число больше, чем 372. Цифра 6 не подходит.

5)     Проверяем цифру 5 : 64 ∙ 5 = 320, 320 < 372. Цифра 5 подходит. Записываем её в частном. Определяем, сколь­ 3 ко десятков разделили: 643 ∙ 5 = 3 215.

6)     Находим остаток: 3 729 –         −3215^3729¼4 64358

– 3 215 = 514. Остаток

514 < 643, значит, циф­ −51445144 ра подобрана верно.

7)     Сносим цифру 4. Второе          0

        неполное    делимое    —                                       8

5 144. Чтобы 5 144 разделить на 643, достаточно 51 разделить на 6. Пробная цифра 8.

8)     Проверяем цифру 8 : 643 ∙ 8 =          ³²

           = 5 144. Цифра 8 подходит.           ^{× 643}8

9)     Читаем ответ: частное равно   5144

58.

0

                                 На    5    делятся    все    числа,    которые

оканчиваются на 0 или 5.

70 делится на 5 без остатка, потому что оканчивается цифрой 0:

70 : 5 = 14

435 делится на 5 без остатка, поэтому 3 что оканчивается цифрой 5:

435 : 5 = 87

На 6 делятся числа, которые делятся

одновременно и на 2, и на 3.

51 042 делится на 2, потому что оканчивается на 2.

8                   51 042 делится на 3, потому что

(5 + 1 + 0 + 4 + 2) : 3 = 12 : 3 = 4

Значит, число 51 042 делится на 6 без остатка.

51 042 : 6 = 8507

На 9 делятся числа, сумма цифр ко­

торых делится на 9.

Например:

0                   16 074 делится на 9, потому что

(1 + 6 + 0 + 7 + 4) : 9 = 18 : 9 = 2 16 074 : 9 = 1 786

Математика

Именованные числа

Именованные числа — это числа, полученные          при   измерении величин и сопровождающиеся названием единицы измерения. Например: 2 кг, 4 см, 8 л.

Именованные числа бывают простые 3 и составные.

Простые именованные числа: 7 м, 18 т, 21 кг, 15 л — в них входит только одна единица измерения.

Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м — в них входят несколько единиц измерения.

8

Преобразования именованных чисел

Составные именованные числа можно преобразовать в простые:

1     м 6 дм = 16 дм

Некоторые простые именованные чис­

                 ла можно преобразовать в составные:                   0

2     350 г = 2 кг 350 г

Выражения

Математическое выражение — это

фраза, записанная с помощью чисел, знаков и букв.

Выражение, записанное только с по­

³        ловыммощью чисел и знаков, называется . чис­

Выражение, в котором кроме чисел

и знаков есть буквы, называется буквенным.

                                Любое     числовое     выражение    имеет

значение. Найти значение числового выражения — значит найти его ответ.

8

Порядок действий в выражениях

В выражениях без скобок, где выполняются только сложе ние и вычитание, действия выполняют в том порядке, в котором они записаны (то есть слева направо).

0                                       1          2

70 – 26 + 10 = 54

Математика

Учимся решать задачи

Все задачи делятся на простые и составные.

Простая задача — это задача, которая решается в одно действие.

Составная задача — это задача, для 3 решения которой нужно выполнить несколько связанных между собой действий.

Как работать над задачей

1.     Прочитай внимательно условие задачи

                          и представь то, о чём идёт речь.                        8

2.     Запиши          кратко        задачу       или   сделай к ней рисунок, схему, чертёж.

3.     Объясни, что означает каждое число.

4.     Подумай, можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что нужно знать, чтобы ответить на вопрос задачи?

5.     Устно составь план решения задачи.

6.     Реши задачу и найди ответ.

7.     Проверь решение, составив обратную 0 задачу.

8.     Запиши ответ.

Составные задачи

Составные задачи состоят из нескольких простых и решаются в два и больше действия.

Решение таких задач можно записы­

3            вать по действиям или выражением._{Если решение задачи записывается по} действиям, то в каждом действии, кроме последнего, нужно записать пояснение.

Рыбак поймал 10 щук, а лещей на 8 больше. Сколько всего рыб поймал рыбак?

8                                     Схема к задаче:

I       —  

II    — ? на    больше     ^?

Краткое условие:

Щук — 10

                            Лещей — ? на 8 больше          ^?

Схема анализа задачи:

Главный вопрос задачи обводим кружочком. Далее рассуждаем так:

0 — Можем ли мы сразу ответить на вопрос задачи?

— Нет.

                         Краткое условие:              Схема к задаче:

                            3 ящ. — по 6 кг                   по        

                                                                                   ?                            ?

                            5 ящ. — по 8 кг                    по

Схема анализа задачи:

— Можем ли мы сразу ответить на во­

3                  прос задачи?

— Нет.

— Почему?

— Потому что мы не знаем, сколько килограммов огурцов в 3 ящиках и 5 ящи ­ ках отдельно?

— Можем ли мы узнать, сколько огурцов 8 — Да.в 3 ящиках?

— Каким действием?

— Умножением, потому что по 6 кг 3 раза.

— Можем ли мы узнать, сколько килограммов огурцов в 5 ящиках?

— Да. Для этого нужно 8 умножить на 5, потому что по 8 кг 5 раз.

— Каким действием ответим на вопрос задачи?

0             — Сложением, потому что находим сумму.

Краткое условие к этой задаче можно записать в виде таблицы:

Математика

Составные задачи на зависимость между величинами «цена», «количество», «стоимость»

 В магазине Миша за 9 пакетов сока

заплатил 360 руб. За столько же па­

кетов молока он заплатил 297 руб. На 3 сколько пакет молока дороже, чем пакет сока?

Составим краткое условие в виде таблицы.

Стои­

           Продукты        Цена       Коли чество

мость

8

Сок ?  на ? 9 пакетов 360 руб. Молоко ? больше столько же 297 руб.

Решение.

1)     360 : 9 = 40 (руб.) — цена 1 пакета сока

2)     297 : 9 = 33 (руб.) — цена 1 пакета молока

3)     40 – 33 = 7 (руб.) Выражение:

                                         360 : 9 – 297 : 9 = 7 (руб.)                            0

Ответ: на 7 руб. дороже.

Математика

рой — 14 км/ч. На каком расстоянии находятся посёлки?

3

Схема анализа задачи:

1-й способ

— О чём говорится в задаче?

— О движении двух лыжников. Поэтому краткое условие к задаче оформляем в виде рисунка.

——  Что известно о начале движения?Лыжники начали двигаться одно­ 8 временно. Покажем это стрелочками «навстречу».

Выводы:

1.     Расстояние между лыжниками всё время уменьшается.

2.     Всё расстояние складывается из расстояния, которое прошёл первый лыжник, и расстояния, которое

                               прошёл второй лыжник.                                   0

3.     Лыжники начали и закончили движение одновременно, поэтому они

 Два лыжника одновременно вышли из пункта A в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй — 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

3

Решение.

1-й способ

8 1) 12 ∙ 3 = 36 (км) — расстояние, которое прошёл первый лыжник за 3 ч

2) 14 ∙ 3 = 42 (км) — расстояние, которое прошёл второй лыжник за 3 ч 3) 36 + 42 = 78 (км)

Ответ: 78 км — расстояние между лыжниками через 3 ч.

2-й способ. Обрати внимание, что расстояние, которое проходят лыжники за

0                 1 ч при движении в противоположных

направлениях, называется скоростью уда-

ления.

Èçäàíèå äëÿ äîïîëíèòåëüíîãî îáðàçîâàíèÿ

Äëÿ ìëàäøåãî øêîëüíîãî âîçðàñòà

ÍÀÃËßÄÍÎ È ÄÎÑÒÓÏÍÎ. ÍÀ×ÀËÜÍÀß ØÊÎËÀ

Ìàð÷åíêî Èðèíà Ñòåïàíîâíà

ÌÀÒÅÌÀÒÈÊÀ

1—4êëàññû

Âñõåìàõèòàáëèöàõ

Äèðåêòîð ðåäàêöèè Ë. Áåðøèäñêèé

Îòâåòñòâåííûé ðåäàêòîð À. Æèëèíñêàÿ Ðåäàêòîð À. Ðóäíåâà

Õóäîæåñòâåííûé ðåäàêòîð Í. Áèðæàêîâ

Âåðñòêà Í. Ñóõàðåâ

Êîððåêòîð Í. Ñòàíèáóëà

Ïîäïèñàíî â ïå÷àòü 17.11.2010. Ôîðìàò 60õ90 ¹/₁₆.

Ïå÷àòüîôñåòíàÿ.Áóì.îôñ.Óñë.ïå÷.ë.9,0.

                       Òèðàæ             ýêç. Çàêàç