Самарский колледж строительства и предпринимательства (филиал)

федерального государственного бюджетного образовательного учреждения высшего образования

"Национальный исследовательский

Московский государственный строительный университет"

 

 

 

 

 

 

 

 

 

 

 

 

 

Материал для факультатива

 

по математике

для студентов 1 курса

                                                  

«Красота и магия числа»

 

 

 

 

 

 

 

 

Автор: преподаватель высшей квалификационной категории

СКСП ФГБОУ ВО «НИ МГСУ»

Буркина Дилара Дамировна

 

 

 

 

 

 

 

 

 

2022

 

 

«Бог создал натуральные числа,

всё остальное – дело рук человеческих»

Немецкий математик

Леопольд Кронекер (1823-1891)

 

Мы имеем дело с числами с самого раннего детства и на протяжении всей жизни, независимо от рода деятельности. Но что такое число и какие же бывают числа? Попробуем ответить на эти вопросы в этой работе. Разберем историю развития чисел, познакомимся с понятием комплексного числа и удивимся некоторым интересным числам, увидев их красоту и магию…

Число – основополагающий термин в математике. С первобытных времен  числа казались людям чем-то таинственным и магическим, ведь любой предмет можно было увидеть и потрогать, а число потрогать нельзя, но тем не менее числа реально существуют. Пифагорейцы считали, что числа – это математические абстракции, которые руководят миром, что любую закономерность можно выразить с помощью чисел, что числа устанавливают порядок в мире.

Каждый раз с открытием новых чисел, им приписывались такие свойства как сверхъестественность, мистичность, нереальность. На протяжении многих веков, с самого начала развития человечества, люди подчинялись числам, подчиняя их себе.

 

Краткая история развития чисел

 

Древнегреческие математики считали «настоящими» только натуральные числа. Натуральные числа (от лат. naturalis  — естественный) — числа, возникающие естественным образом при счёте.

Называемые теперь натуральными, эти числа появились в глубокой древности, они возникли из практических нужд человека, когда возникла потребность в счете предметов. На ранних ступенях развития общества люди не умели считать, они отличали совокупности двух и трёх предметов, а если предметов было больше, то люди говорили «много». Расширение запаса чисел на первых порах происходило медленно. Число «семь» долгое время считалось очень большим. Затем пределом счёта было число «сорок», оно означало неопределённо большое количество. Далее это же значение приобрело число «сто». Число «десять тысяч» в старину называли «тьмой». Постепенно количество натуральных чисел увеличивалось и было установлено, что это множество бесконечно.

 

Одновременно с натуральными числами широко применялись дроби, которые возникли из потребности оперировать частями целого. При разделе добычи и при измерении величин у людей возникла необходимость использовать «ломаные числа» - обыкновенные дроби, которые применялисьв практических расчетах уже во 2 веке до н.э. в Древнем Египте и Древнем Вавилоне. Настоящее обозначение дробей и действия над ними впервые были изложены учеными из мусульманских стран в 9 веке. Десятичные дроби появились значительно позже, в 14-15 веках, в Средней Азии.

 

Запас натуральных и дробных чисел вполне достаточен, чтобы производить практические измерения, но для теории измерений этого запаса мало. Открытие, сделанное одним из пифагорейцев во 2 веке до н.э., перевернуло представление о числе. Он доказал, что диагональ квадрата несоизмерима со стороной этого квадрата, так как, чтобы вычислить длину диагонали квадрата со стороной 1 м, нужно решить уравнение х²=2. Никакое натуральное число и никакая дробь не может удовлетворить этому уравнению. Значит, либо нужно довольствоваться неточным значением, либо ввести новые числа, которые являлись бы корнями таких уравнений. После длительной борьбы этих двух точек зрения победила вторая. Считается, что именно это открытие положило начало теоретической математики (до этого математика носила лишь практический характер). Так возникли иррациональные числа – числа, которые нельзя представить в виде обыкновенных дробей (дословный перевод термина «иррациональное число» - не имеющее отношения). В противоположность таким числам термин «рациональное число» стала носить обыкновенная дробь, которая является отношением. Прошла не одна сотня лет, как математики смогли установить способ записи иррационального числа в виде бесконечной непериодической десятичной дроби.

 

Следующим важным этапом в развитии понятия числа было введение отрицательных чисел, которые появились позже обыкновенных дробей. Первые упоминания об отрицательных числах встречаются у китайских математиков во 2-1 веках до н.э. Далее, в 5-6 веках отрицательные числа очень широко использовались в Индии, с ними производили вычисления и они не казались необычными. Положительные числа тогда толковались как имущество и прибыль, а отрицательные – как долг и убыток. А в Китае относились к отрицательным числам с осторожностью, лишний раз старались их не применять. Вычитание из числа 3 числа 5 долгое время считалось не просто невозможным, но и бессмысленным.

Так и в Европе, отрицательные числа не признавали очень долго и считали их «мнимыми» и «абсурдными». Считали, что 0 – это пустота, а ничего нет меньше пустоты. И если при вычислении все же получалось отрицательное число, считалось, что решения нет. Первым в Европе отрицательные числа рассмотрел Леонардо Пизанский (Фибоначчи) в 13 веке. Многие выдающиеся математики первое время отказывались вводить их в употребление или вводили с большой неохотой. Даже Декарт в 17 веке называл сначала отрицательные числа «ложными числами», но потом предложил откладывать их на числовой прямой слева от нуля. Число 0 стали трактовать как границу между «истинными» и «ложными» числами, которые вместе с нулем стали составлять множество целых чисел.

Сформировалось и множество действительных (вещественных) чисел, которое включало в себя рациональные и иррациональные числа.

 

С течением времени возникла необходимость расширить множество действительных чисел. Это связано прежде всего с решением практических задач, а именно с решением квадратных уравнений. Ведь даже такое простое квадратное уравнение как  х²+1=0 не имеет корней во множестве действительных чисел, так как для его решения надо выполнить невозможную операцию - извлечь квадратный корень из -1, а такого действительного числа как не существует.

О таких числах, как и т.д. заговорили ещё в 16 веке и называли их «нереальными». Итальянские математики 16-го века Кардано и Бомбелли, решая квадратное уравнение х²+1=0 ввели в рассмотрение символ .Символ «i» предложил Леонард Эйлер в 1777 году, взявший для этого первую букву латинского слова imaginarium, что означает «мнимый», «воображаемый». Число i=называется мнимой единицей, это число, которое не является действительным числом. Долгое время учёные не могли признать мнимые числа. Природа таких чисел не была разгадана и к ним относились как к какому-то сверхъестественному явлению в математике. Если уж к отрицательным числам

(-1, -2, -3, …) до 17 века относились недоверчиво и называли их «ложными», то можно себе представить, как относились к мнимым числам (,), ведь уже в 8 веке было установлено, что квадратный корень из положительного числа существует, а из отрицательного – нет.

Таким образом, множество действительных чисел было расширено до такого множества, в котором извлекались корни четной степени из отрицательных чисел. Это множество называется множеством комплексных чисел (от лат. complexus – совокупность, сочетание).

 

Основные числовые множества и отношения между ними можно выразить с помощью математических символов так:

N – множество натуральных чисел,

Z– множество целых чисел,

Q – множество рациональных чисел,

I – множество иррациональных чисел,

R – множество действительных чисел,

С – множество комплексных чисел.

 

N⊂ Z⊂ Q⊂ R⊂ С,      I⊂ R,      Q∪ I = R,      Q ∩ I = ∅

 

Каждый раз новые числа воспринимались как нечто необычное, мнимое и даже мистическое. Люди испытывали страх перед новыми числами, старались их не использовать или свести их применение к минимуму. Какие только термины не придумывали люди новым числам: «ложные», «нереальные», «мнимые», «тьма». Но в то же время ученых пленило непреодолимое желание исследовать новые числа, узнать больше о них, подчинить их себе… И люди подчиняли себе числа и одновременно подчинялись им сами: так было сначала с «тьмой», затем с иррациональными числами, с отрицательными числами, а потом и с комплексными.

 

 

 

 

 

Немного о комплексных числах

 

Комплекснымчислом z в алгебраической форме называется выражение следующего вида: z = x+yi, где x,y- действительные числа.

i— это мнимая единица, определяемая равенством i² = –1.

 

Число x —действительная часть комплексного числа z;

выражение yi —мнимая часть комплексного числа z;

ż = х- yi— комплексно сопряженное число числу z;

-z = - х - yi— противоположное число числу z;

0 = 0 + 0i— комплексный ноль;

Примеры.

1)    z = -2 +7i,  x = -2, y = 7,  ż = -2- 7i, -z= 2 – 7i;

если x ≠ 0 и y≠ 0, то число называется комплексным;

2)    z = 5 + 0i = 5,  x = 5, y = 0,ż = 5 – 0i = 5,  -z= –5 – 0i = –5

если y = 0, то z = x — действительное число;

3)    z = 0 - 3i = -3i,  x = 0, y = -3, ż = 0 + 3i = +3i, -z = –0 + 3i = 3i

если x = 0, то z = yi — мнимое число.

 

Над комплексными числами можно выполнять все те же арифметические действия, что и над действительными числами.

При сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.

Примеры.

1) (1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i;

2) (1 + 2i) – (2 – 5i) = 1 + 2i – 2 + 5i = –1 + 7i.

При сложении комплексно сопряжённых чисел получается действительное число.

Пример.(1 + 2i) + (1 – 2i) = 1 + 2i + 1 - 2i = 1 + 1 = 2.

Умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой i² = -1 и приведением подобных по действительным и мнимым частям слагаемым.

Примеры.

1)    (1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i² = 2 – 3i + 2i + 3 = 5 – i;

2)    (2 + i)² = 2² + 4i + i² = 3 + 4i.

При умножении комплексно сопряжённых чисел получается действительное число.

Пример.(1 + 4i)∙(1 – 4i) = 1 – 4²i² = 1 + 16 = 17;

При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:

Пример.

 

Степени числа i.

i⁰ = 1        i⁴ = 1      …  i⁴ⁿ = 1

i¹ = i         i⁵ = i       …  i⁴ⁿ⁺¹ = i

i² = -1       i⁶ = -1     …  i⁴ⁿ⁺² = -1

i³ = -i        i⁷ = -i      …  i⁴ⁿ⁺³ = -i

Пример. Вычислить i¹²³ = i^4*30+3 = -i.

 

Решение квадратных уравнений.

Благодаря символу i= стало возможным извлекать квадратные корни из отрицательных чисел, а значит и решать квадратные уравнения с отрицательным дискриминантом.

Пример.

Таким образом, во множестве комплексных чисел решается любое квадратное уравнение. Если D>0, то квадратное уравнение имеет два действительных корня, если D=0, то уравнение имеет один действительный корень, если D<0, то квадратное уравнение не имеет действительных корней, но имеет два комплексно-сопряжённых корня.

 

Особенностью комплексных чисел является то, что их невозможно сравнить.

Для того, чтобы возводить комплексные числа в степень и извлекать корни из комплексных чисел, нужно их представить в тригонометрической форме.

Каждому комплексному числу соответствует единственная точка на координатной плоскости. Плоскость, служащая для изображения комплексных чисел, называется комплексной плоскостью, ось ОХ называется действительной осью, ось ОУ - мнимой осью.

                    z = x+yi  A (x; y)

Пример.  z₁= -2 + 3i   A (-2; 3)

              z₂ = 4 - iB (4; -1)

              z₃ = 2iC (0; 2)

              z₄ = -5    D (-5; 0) 

Изобразив в комплексной плоскости точки, соответствующие этим комплексным числам, можно увидеть, насколько множество С шире множества R, ведь действительные числазанимают во всей комплексной плоскости только действительную ось ОХ, а комплексные числа – всю плоскость.

 

 

 

Некоторые интересные числа

 

Число е

 

Число е ≈ 2,718281828459045..., математическая константа, основание натурального логарифма, называется неперовым числом, в честь шотландского математика Д. Непера, который изобрел логарифмы (1614 г). Но это обозначение ввел Л. Эйлер в 1736 году, поэтому число е ещё называют эйлеровым числом. Число е играет очень важную роль в математическом анализе. Число е – иррациональное, трансцендентное.

1.  Второй замечательный предел  ;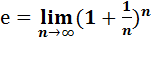

2.   Касательная, проведенная к графику показательной функции с основанием е, называемой экспонентой, у=е^х, в точке х₀=0 образует угол 45^о с положительным направлением оси Ох;

3.   Функция равна своей производной (е^х)^' = е^х;

4.   Интересный пример: вкладчик положил на счет в банке сумму 1 рубль со процентной ставкой 100% годовых.

Если начислить один раз в год сразу 100%, то он получит сумму 1руб+100%=2руб.

Если начислять два раза в год по 50%, то он получит сумму 1руб+50%+50%=2,25руб.

Если начислять 4 раза в год по 25%, то он получит сумму 1руб+25%+25%+25%+25%=2,44140625 руб.

И так далее. Если количество начислений в год будет стремится к бесконечности, то сумма, которую получит вкладчик будет стремиться к числу е.

 

Число π

 

Число π ≈ 3,14159265358979…, математическая константа, иррациональное, трансцендентное число, равное отношению длины окружности к длине ее диаметра, «число Лудольфа», «круговая постоянная», «архимедова константа».

Число π существует почти столько, сколько существует математика. Конечно, точное значение числа рассчитали не сразу. Поначалу отношение длины окружности к диаметру считали равным 3. Уже 4 000 лет назад у π было значение — оно равнялось 3,125, арабские математики считали π ≈ 3,162.Но с течением времени, когда начала развиваться архитектура, потребовалось более точное измерение. Кстати, число существовало, а вот буквенное обозначение оно получило только в начале 18 века (1706 год) и происходит от начальных букв двух греческих слов, означающих «окружность» и «периметр». Буквой "π" число наделил математик У. Джонс, а вот окончательно символ закрепился в математике уже в 1737 году, когда ученый Леонард Эйлер включил его в один из своих трудов по тригонометрии.

Число π называется «числом Лудольфа», так как в 1596 году голландский вычислитель Лудольфван Цейлен определил 32 знака после запятой числа π, на эти вычисления он затратил 10 лет.

14 марта во всем мире с 1988 года отмечают необычный праздник – День числа π, так как в этой дате месяц и число образуют 3.14.

А еще 14 марта в 1879 году на свет появился Альберт Эйнштейн — отец теории относительности.

Еще одной датой, связанной с числом π, является 22 июля, 22/7, День приближенного числа π ,так как π ≈ .

Мистическое значение числа π проявляется в том, что если сложить 144 цифры после запятой в числе π, то получится число 666 – «число зверя», это при том, что 144=(6+6)*(6+6), что придает еще больше мистичности.

 

Простые числа

 

Простое число – это число, которое имеет только два делителя: 1 и само это число. Первые простые числа: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,…

До сих пор математики не знают формулы, с помощью которой можно получить простые числа одно за другим. Уже в 3 веке до н.э. александрийский ученый Эратосфен задумался над тем, как составить список простых чисел, в связи с чем его имя вошло в науку. В древности писали на восковых табличках острой палочкой-стилем, поэтому Эратосфен «выкалывал» составные числа острым концом стиля. После выкалывания всех составных чисел таблица напоминала решето. Отсюда и название «решето Эратосфена».

 

Совершенные числа

 

Совершенное число — натуральное число, равное сумме всех своих собственных делителей (т. е. всех положительных делителей, отличных от самого числа).

Первое совершенное число — 6 (1 + 2 + 3 = 6), следующее — 28 (1 + 2 + 4 + 7 + 14 = 28). По мере того как натуральные числа возрастают, совершенные числа встречаются всё реже. Третье совершенное число — 496, четвёртое — 8128, пятое — 33 550 336, шестое — 8 589 869 056 . Люди усматривали в совершенстве чисел 6 и 28 особый смысл. Разве не за 6 дней был сотворен мир, восклицали они, и разве Луна обновляется не за 28 суток?

Наличие нечетного совершенного числа и существование наибольшего совершенного числа – не доказаны.

 

Число 365

 

365 = 10² + 11² + 12² = 100 + 121 + 144

365 = 13² + 14² = 169 + 196

 

 

Дружественные числа

 

Это такие два числа, каждое из которых равно сумме делителей второго дружественного числа. Наименьшие из дружественных чисел 220 и 284 были известны еще пифагорейцам, которые считали их символом дружбы. Следующая пара дружественных чисел 17296 и 18416 была открыта французским юристом и математиком Пьером Ферма лишь в 1636 году, а последующие числа находили Декарт, Эйлер и Лежандр. 16-летний итальянец Николо Паганини (тезка знаменитого скрипача) в 1867 году потряс математический мир сообщением о том, что числа 1184 и 1210 дружественные! Эту пару, ближайшую к 220 и 284, проглядели все знаменитые математики, изучавшие дружественные числа.

 

Число 999

 

Особенность числа 999 в том, что его можно легко умножить на трёхзначные числа. Тогда получится шестизначное произведение: первые три цифры его есть умножаемое число, уменьшенное на единицу, а остальные три цифры являются дополнениями первых трех до 9. Например,

573 ∙ 999 = 572427

Число 1001

 

Сначала рассмотрим число 1001. Это число сказок, которое царица Шехерезада рассказывала царю Шахрияру.

1001 = 7 ∙ 11 ∙ 13.

Замечательно то, что если его умножить на любое трехзначное число, то в результате получится тоже самое число, записанное дважды.

247∙1001 = 247∙(1000+1) = 247∙1000+247∙1 = 247000+247 = 247247

 

Число 10101

 

Если любое двузначное число умножить на 10101, то получится это же число, записанное три раза подряд.

39∙10101 = 39∙(10000 + 100 + 1) = 390000 + 3900 + 39 = 393939

 

Число 111111

 

Благодаря знакомству со свойствами числа 1001 мы сразу видим, что

111111 = 111 ∙ 1001

Но мы знаем, что

111 = 3 ∙ 37, 1001 = 7 ∙ 11 ∙ 13

Отсюда следует, что наша новая числовая диковинка, состоящая из одних единиц, представляет собой произведение пяти простых множителей

111111 = 3 ∙ 7 ∙ 11 ∙ 13 ∙ 37

 

 

 

Число 666

 

Мы не будем останавливаться на мистической составляющей числа 666 - об этом и так написано огромное количество материала. Отметим лишь математическую ипостась числа Зверя.

Число 666 обладает громадным набором поистине уникальных математических свойств, которых, по различным исследованиям, насчитывают около 100. Ниже приведем лишь самые примечательные из них:

 

1. Простых делителей у числа 666 всего три : 2, 3 и 37. Обратите внимание на равенство:  2∙3∙3∙37 = 666   и следующее из него 2+3+3+3+7 = 6+6+6

 

2. Число "зверя" входит в интересную "пифагорову тройку" (216, 630, 666), то есть 216² + 630² = 666², причем   216 = 6∙6∙6,   630 = 666 – 6∙6

Итого (6∙6∙6)² + (666 – 6∙6)² = 666²

 

3. Это равенство очень уж мне нравится:  333² + 444² + 555² = 666²

 

4. Невероятно красивый факт. Если сложить первые 666 простых чисел-палиндромов (например, 11311, 17971 и т.д.), то получится число 2391951273. Казалось бы, и что, однако, складывая кубы всех цифр этого числа, получим: 

2³ + 3³ + 9³ + 1³ + 9³ + 5³ + 1³ + 2³ + 7³ + 3³ = 666 + 666 + 666

 

5. Число зверя является суммой квадратов первых семи простых чисел:

2² + 3² + 5² + 7² + 11² + 13² + 17² = 666

 

6. Еще парочка красивых свойств без пояснений:  1⁶ – 2⁶ + 3⁶ = 666

 

1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 5³ + 4³ + 3³ + 2³ + 1³ = 666

 

Числа Кита

 

Чаще всего, когда мы говорим о числах, мы подразумеваем бесконечное их количество. Но этих чисел до сих пор найдено всего 100 штук! Автором идеи и первооткрывателем этих чисел является Майк Кит - американский математик, автор более 60 патентов и книги, которая кодирует первые 10000 знаков числа Пи.

Идея Кита состояла в том, чтобы раскладывать числа следующим образом: сначала записываются знаки десятичной записи числа N, затем вычисляется их сумма и записывается справа (вторая строчка рисунка). В приведенном выше варианте суммируется 3 числа, так как взято трехзначное число. Если в получившемся ряду присутствует изначальное число N, то такое число и называется числом Кита.

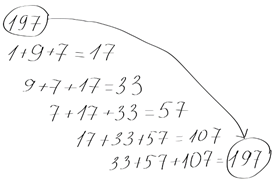
На данный момент известно всего 100 (!!!) чисел Кита, потому так и не разработано алгоритма, который может их найти, кроме как обычным перебором. Первые из них: 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, 31331, 34285, 34348, 55604, 62662.

До сих пор неизвестно, бесконечно ли количество чисел Кита или нет. Найдено пока лишь 3 кластера Кита: групп чисел Кита, кратных друг другу: (14, 28), (1104, 2208) и (31331, 62662, 93993).

 

Проблема числа 10958

 

Есть один занимательный факт, который обнаружил бразильский математик Индер Танежи - неразложимость числа 10958 определенным им способом.

Индер в своей 161-страничной работе "Crazy Sequential Representation: Numbers from 0 to 11111 in terms of Increasing and Decreasing Orders of 1 to 9" рассматривает разложение чисел в прямом и обратном порядке следования цифр. Давайте рассмотрим на простом примере:

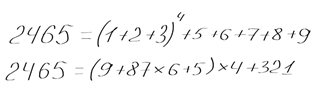
Для представления чисел допускается использовать цифры от 1 до 9 в прямом и обратном порядках, бинарные операции (+, -, *, возведение в степень) и конкатенацию (только в таком виде, как показано выше).

Индер Танежа таким образом описал разложения для всех чисел до 11111, но к великому удивлению осталось одно пятно. Вот оно:

 

10958 - полупростое число: у него из делителей только 2 и 5479. Кстати, с представлением 5479 проблем нет.

На данный момент не существует решения проблемы разложения числа 10958, причем наиболее разработанные направления относятся к доказательству отсутствия такого представления.

Кстати, на существующих компьютерах решить задачу Танежи не получится.

Самое удивительное в том, что проблема числа 10958 стала основой для формирования отдельной математической теории - теории конечно-трансцендентных чисел и частью нового математического аппарата в программировании и алгебраической топологии.

 

Самое удивительное число в мире 142857

 

Тайна чисел повсюду. Что удивительного в числе 142857? На первый взгляд может показаться, что это просто набор цифр, которые не связаны между собой. Однако у этого числа есть удивительные свойства.

 

Факт 1. Число 142857 является циклическим при умножении на однозначные числа. Если данное число умножать на 1, 2, 3, 4 и так далее до 7, то цифры 1, 4, 2, 8, 5 и 7 будут так и оставаться в произведении. Более того, цифры в числе как бы смещаются со своих мест по кругу. Поэтому такие числа и называются циклическими   ·         142 857 ×  1 = 142 857 ·         142 857 ×  2 = 285 714 ·         142 857 ×  3 = 428 571 ·         142 857 ×  4 = 571 428 ·         142 857 ×  5 = 714 285 ·         142 857 ×  6 = 857 142	Факт 2. Число 142857 появилось путем деления единицы на семь, или другими более формальными словами, оно является периодом разложения обыкновенной дроби 1/7 в десятичную дробь. А также если делить на 7 числа 1, 2, 3, 4, 5, 6, то мы получим эту же последовательность цифр   1/7 = 0,142857142857… = 0,(142857) 2/7 = 0,285714285714… = 0,(285714) 3/7 = 0,428571428571… = 0,(428571) 4/7 = 0,571428571428… = 0,(571428) 5/7 = 0,714285714285… = 0,(714285) ·         6/7 = 0,857142857142… = 0,(857142)
Факт 3. У числа 142857 есть множество примеров цикличности. 8572 – 1422 = 714285 1428572 = 20 408 122 449,       но 20 408 + 122 449 = 142857 142857 / 2 = 71 428, 5 142857 / 5 = 28 571, 4	Факт 4. Суммы частей числа 142857 дают числа из девяток. ·         1 + 8 = 4 + 5 = 2 + 7 = 9 ·         14 + 28 + 57 = 99 ·         142 + 857 = 999 0,142 857 × 7 = 0,999999                   142857 × 7 = 999999
Факт 5. Соотношение сторон листа формата А4 является десятичной дробью с периодом, равным числу 142857.  Так стандартная длина листа А4 равняется 297 мм, а ширина составляет 210 мм. Отношение длины к ширине листа, выглядит следующим образом 297/210 = 1,4(142857)	Факт 6. Число 142857 является числом харшад.  Числами харшад называются числа, делящиеся нацело на сумму цифр, из которых они состоят.                         27

 

Как связаны числа π и 5 ?

 

Напомним первые цифры в записи числа π ≈ 3,1415926535897932384626…

А теперь возьмем в руки калькулятор и посчитаем такие выражения:

1/5 = 0,2

1/55 = 0,018181818… = 0,0(18)

1/555 = 0,0018018018108… = 0,0(018)

1/5555 = 0,0001800180018… = 0,0(0018)

1/55555 = 0,0000180001800018… = 0,0(00018)

1/555555 = 0,0000018000018000018… = 0,0(000018) ≈ 180 ∙ 10^-8

 

А потом вычислим синусы получившихся значений:

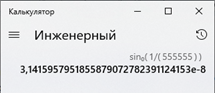Sin (1/5) ≈ 0,0034906514 = 3,4906514 ∙ 10^-3

Sin (1/55) ≈ 0,0003173326 = 3,173326 ∙ 10^-4

Sin (1/555) ≈ 0,0000314474 = 3,14474 ∙ 10^-5

Sin (1/5555) ≈ 0,0000031419 = 3,1419 ∙ 10^-6

Sin (1/55555) ≈ 0,0000003141624 = 3,141624 ∙ 10^-7

Sin (1/555555) ≈ 0,0000000314159579 = 3,14159579 ∙ 10^-8

 

Ничего не напоминает?  (вычисления проводятся в градусах)

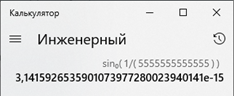
Для интереса вычислим то же самое для числа с 13-ю пятерками. Красивый результат, не правда ли? 

Мы всегда получаем число, близкое к числу π за исключением множителя 10^-n. И чем больше пятёрок, тем результат будет ближе к точному значению числа π.

Это кажется удивительным. НО!

У данного математического факта есть логическое объяснение.

 

Пусть Х – это угол в градусах.

Х = 1/555555 = 0,0000018000018000018… = 0,0(000018) ≈ 180 ∙ 10^-8

Вспомним формулу перевода градусов в радианы

Вспомним график функции У = Sin Х  и его важное свойство: при малых значениях аргумента Х график функции почти сливается с прямой линией У = Х. То есть для малых значений аргумента получаем 

Тогда  Sin Х = Sin (1/555555 градусов) = Sin () =

                      = Sin () ≈ .

 

 

Много есть красивых чисел, интересных свойств и мистических особенностей этих чисел.

 

Напоследок стихотворение, написанное автором статьи.

 

             «Числа»

 

Есть числа натуральные,

Есть иррациональные,

С действительными числами

Знакомы мы давно.

 

А есть ещё комплексные

Числа интересные,

Очень необычные,

Пока нам непривычные,

Но красивые всё равно.

 

Чтоб смогли решить задачу,

Чтобы посчитали сдачу,

Числа нам нужны везде,

И на суше, и в воде.

 

Целые, простые,

Дробные, составные,

Действительные, мнимые,

По-своему красивые.

 

Время очень быстротечно,

Но какая б эра не пришла

Люди будут видеть вечно

Красоту и магию числа!        (автор Буркина Д.Д.)

 

Скачано с www.znanio.ru